计学习理论已经发展了几十年了,最近二十年的感觉是它的繁荣期。我在这一块耗费的时间也多了点,虽然只是草草入门了解,但亦觉得受益良多。
虽然提及统计学习理论的文章多会搭上神经网络的弱点,但是神经网络虽然存在理论上的梯度下降的固有缺陷,可应用起来的效果倒很不错的说。从一个方面来讲,统计学习在可行性的极限上与神经网络没啥区别,跟傅立叶变换这个基础关系很紧密。另外,统计学习理论对于小样本学习的情况比较关注,毕竟现实中样本经常是不够的,所以可以说它的理论成果比较坚实点。
反问题(由结果推原因)很多情况下是病态的,得到的结果跟样本的关系很大,可能样本有一点小小的偏差,那么结果就差的很远,或许这正是过拟合成为问题的理论来源。在此情况下,对样本的处理过程中需要用到正则化理论(通俗讲就是得到近似解)。一说最小二乘法相信你就能很好联系起来了。
对于正则化应用,除了应用样本的数据,后面通常会加上一个惩罚因子,来对拟合进行调节,以期综合性的筛选出最优化的解。在分类问题上的表现就是结构风险最小化(相对经验风险最小化),通常会控制函数的复杂性,因为复杂性通常和过拟合相联系,为了推广性,通常简单性与光滑性是我们所期望的。
后面的内容主要发生在希尔伯特空间。
这个空间所定义的内积空间是对欧氏空间的推广,在其中的元素是函数时(成为一个函数空间),最有意义,不然退回到欧式空间得了,再提一下,里面的元素具有线性性质,加法与标量乘法。
Riesz representation theorem:
在希尔伯特空间(H)中存在一个元素y,使得其对偶空间(构成元素是连续线性泛函)的元素可以表示成这样的形式,h = <x, y>, x是H中的任意一个元素,且可唯一表示成这种形式。对偶空间中的值是实数。我想这个定理是如此的重要,在函数分析领域,你可以把y看作空间的标准正交基的傅立叶级数形式,就不难理解了。
评估泛函的连续性和有界是等同的,所以里斯表示定理说的就是RKHS的问题。
RKHS(再生核希尔伯特空间)的定义,|Ft [f ]| = |f (t)| <= M * ||f ||,对于空间中任意的f。其实这里的M也是代表那个核函数的模,这里可以看作是|Ft [f ]| = <k, f> <= ||K||*||f||,这个式子是柯西-施瓦兹不等式(Cauchy–Schwarz inequality).
核函数可能在现在的应用文章中广泛出现,由其所牵扯出来的便是再生核希尔伯特空间(RKHS).核的再生性的意义其实是由其可以再造出一个它对应的希尔伯特空间,我曾纳闷核具有再生性(reproducing property),纠结于这特性作用与其本身有什么意义,现在回过头来看自己好傻,或许翻译再制造特性不会让人那么迷惑,可见有老师点拨会少消耗些精力与时间。
希尔伯特空间的理论上世纪初就有了,为无穷维线性方程组和量子力学而设,又不是为模式分类而创造,怎么扯上关系的。当做线性回归的时候来解判别函数的时候,通过转换把权向量可写成训练点的线性组合,可发现来自训练例子的信息由训练点对之间的内积给出,这意味着只需要训练点之间的内积(这里的训练点当然或者多是经过高维变换的点)。
核函数该出场了:
核是一个连续函数k,这个函数对于所有的X中的x,z,满足k(x,z) = <f(x), f(z)>,其中f是从X到(内积)特征空间F的一个映射 f: x --> f(x) 属于F。
这意味着可以计算两个点在特征空间的投影之间的内积,而不用显式地求出它们的坐标,标量值,我们喜欢。其实核函数并不是特意为此理论而造,名字当然来自于更早的起名者,来自于积分方程。
同时RKHS的空间范数||f||可以用来来度量假设空间的复杂度,RKHS 是在正则化理论和统计学习理论之间建立联系的基本工具。
接下来从mercer theorem来入手,把一些东西讲一讲。
Mercer theorem里的积分算子
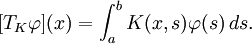
这里的k是一个连续的对称函数,且积分算子Tk:L2(x)-> L2(x)。
因为积分算子是线性的,那么我们就可以谈论它的特征值与特征函数,下面的图片展示的就是积分算子的特征值与特征函数,当然这是对于特征值与特征向量的推广,且下面的e(.)表示的是标准正交特征函数(非零度量空间必有基,有基便必有正交基,这些标准正交特征函数就是作为空间的标准正交基存在)。
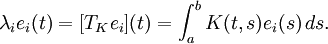
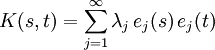
积分算子可以写成这样的一种形式
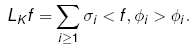 ,几个式子用的符号不一致,请大家海涵海涵,不容易呀。f 的傅里叶级数代入积分算子,式子一分解,特征值就出现在右边,点明一下免得看着突兀。
,几个式子用的符号不一致,请大家海涵海涵,不容易呀。f 的傅里叶级数代入积分算子,式子一分解,特征值就出现在右边,点明一下免得看着突兀。
上面的K(s,t)式子可看作是函数k<s,.>在t点的傅立叶级数。对于许多核K,正的特征值的个数μ是无限的。对应的的RKHS 在2 L 中是稠密的。这意味着这些假设空间是“大的”,因为它们能够任意好的逼近大量函数类。
我们使用RKHS 的一个原因是因为它能够表示一个非常大的假设集合。
Mercer定理通常用来为有效核构造一个特征空间,且它是根据一个显式的特征向量定义特征空间,而不是用RKHS构造的函数定义特征空间。核可以看作是特征空间的元素内积的形式,与此正定核所对应的函数空间,使用归一化的基。
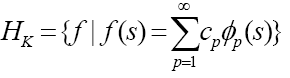 ,
,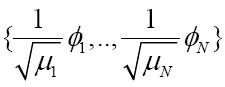
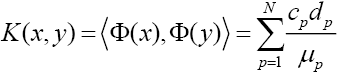
说了这么多,好像没提及模式分类和核函数有啥关系,哈哈,动机来自于感知器模型,通过岭回归的对偶解法,发现特征间的内积包含了所有判断时所要依据的信息。而核函数又有此特性。
还有好多东西可以记,是否还需要追加几章,不确定,还有好多任务没完成。
分享到:









相关推荐
统计学习方法主要涉及模式识别、概率论和统计推断等基础知识。这些方法包括监督学习、无监督学习和半监督学习。书中重点讨论了线性回归、逻辑回归、支持向量机、决策树、随机森林、神经网络、贝叶斯网络等多种模型...
### CCIE笔记——详细命令介绍 #### 一、基本配置命令 在Cisco设备上进行配置时,有许多基本的命令是必须掌握的。这些命令对于设备的初始设置、安全管理以及日常维护至关重要。 - **hostname**: 用于更改路由器的...
3. "作业_chapter3_解答(1).pdf":同理,这是第三章作业的解答,可能涉及模式分类、神经网络或支持向量机等主题,通过这些解答,学习者可以检查自己的理解并学习正确解题思路。 4. "作业_chapter5_解答(1).pdf":第...
- **序列模式**:在数据分析中,序列模式是指在时间序列数据中发现的重复模式或趋势。 - **时间序列**:R语言提供了处理时间序列数据的工具,如`ts()`函数,用于创建时间序列对象。 2. **数据保存和输出格式**: ...
贝叶斯决策方法是统计模式识别中的一个基本方法,用这个方法进行分类时要求:各类别总体的概率分布是已知的;要决策分类的类别数是一定的。在连续情况下,假设对要识别的物理对象有 d 种特征观察量 x1, x2, ⋯, xd,...
3. 随机森林(Random Forests):基于多个决策树的集成学习算法,通过增加模型的多样性来提高预测的准确性和泛化能力。 4. 逻辑回归(Logistic Regression):用于二分类问题的回归分析方法,输出的是样本属于某个...
它基于数据,通过模式识别、统计分析和优化算法,使计算机能够从已有的例子中学习,而不是通过人为编程进行特定任务。机器学习可以分为监督学习、无监督学习、半监督学习和强化学习四大类。 监督学习是最常见的机器...
这个过程涉及模式识别、统计推断和优化算法,旨在让计算机从经验中自我提升。 吴恩达的机器学习课程通常涵盖以下几个核心概念: 1. 监督学习:这是最常见的机器学习类型,包括回归和分类问题。例如,线性回归用于...
解决多分类问题的一个常见方法是利用多个弱分类器通过集成学习(ensemble learning)的方式构建出一个强大的分类器。常用的多分类算法包括决策树、随机森林(random forest)等。 ##### 层次聚类 **层次聚类**...
1. 统计学习理论基础:统计学习方法基于概率论和统计学,它包括监督学习、无监督学习和半监督学习等多种模式。书中首先介绍了学习问题的基本框架,包括实例、特征和假设空间。 2. 感知机:感知机是最早提出的二分类...
以上就是Linux系统中一些常用命令的学习笔记。每个命令后面通常可以跟上不同的选项和参数,来满足不同的需求。掌握这些命令,对于Linux系统的日常运维工作至关重要。随着时间的推移,建议持续学习和实践,不断提高对...
监督学习侧重于通过有标签的训练数据来指导模型学习,预测或分类是其最常见的任务。无监督学习则致力于从无标签数据中发现隐藏的结构或模式,聚类和降维是常见的应用场景。这些学习范式的理解和应用是成为一名优秀AI...
在统计学习理论部分,书中讨论了风险最小化、泛化能力和Vapnik-Chervonenkis(VC)维度等概念,这些理论工具帮助我们理解模型复杂度与泛化能力之间的关系,以及如何通过交叉验证选择最佳模型。 习题解答部分是学习...
这种学习过程通常涉及到统计方法的应用,以从大量数据中提取有用的信息,并基于这些信息做出预测或决策。 机器学习的应用十分广泛,包括但不限于自动驾驶汽车、语音识别、搜索引擎优化、基因组学分析等领域。随着...
标题《机器学习视频笔记》所涉及的知识点非常丰富,涵盖了机器学习领域的多个重要概念和技术,下文将对标题和描述中提及的内容进行详细解读: 1. 机器学习的基本概念 - 什么是机器学习?:机器学习是人工智能的一个...
10. **文本生成**:包括文章摘要、诗歌创作、故事生成等,深度学习模型可以学习语言模式并自动生成连贯的文本。 通过阅读《斯坦福CS224n_自然语言处理与深度学习_笔记_hankcs.pdf》,你可以深入理解这些主题,掌握...
这本书可能会详细讨论特征提取、分类器设计以及模式识别的统计理论,对于想要深入理解模式识别的同学来说,是一本不可或缺的参考书。 在学习过程中,掌握这些知识点不仅能帮助你建立坚实的理论基础,还能提升解决...
3. 主要课程内容:课程内容涵盖了机器学习、数据挖掘和统计模式识别的广泛主题,包括监督学习、无监督学习、机器学习最佳实践等。监督学习部分涵盖参数/非参数算法、支持向量机、核函数、神经网络;无监督学习部分...
本课程总共需要10周时间,分为18节课,涵盖了机器学习、数据挖掘、统计模式识别等广泛的主题。课程中将使用大量的案例研究,并提供包括视频、PPT课件在内的丰富学习资源。作者黄海广作为中国海洋大学2014级博士生,...