hi 欢迎来到小秘课堂第四期,今天我们来讲讲 Authenticated Dynamic Dictionaries in Ethereum 的那些事儿,欢迎主讲人
编辑:vivi
Merkle Tree
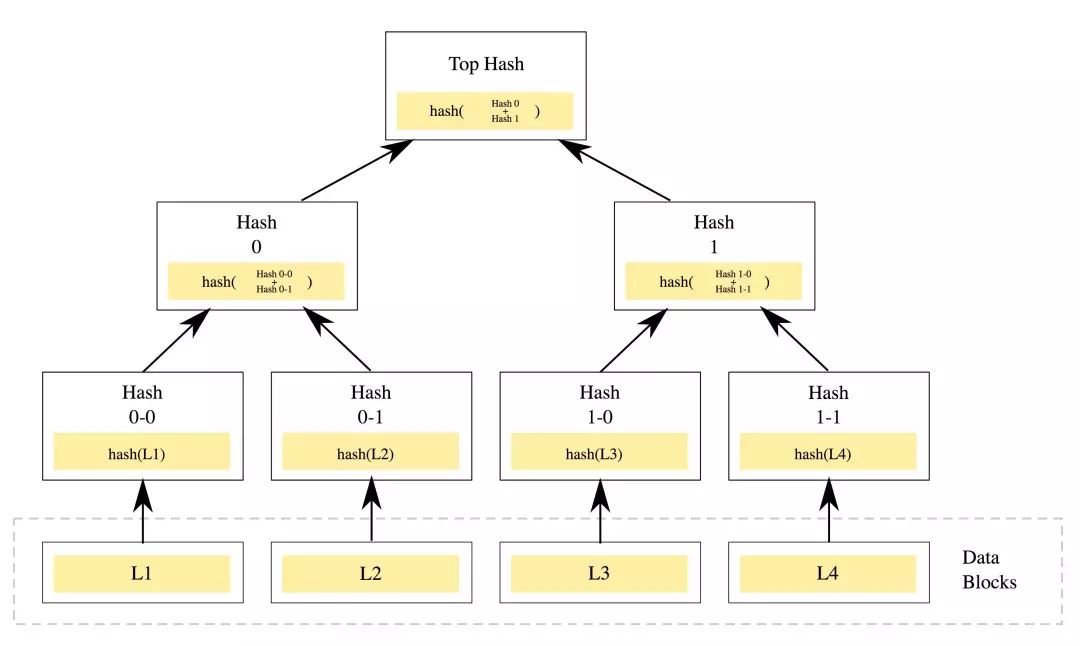
Merkle Tree 是利用 Hash 对内容的正确性进行快速鉴定的数据结构,其结构示意图如下:
-
Merkle Tree 父节点包含所有子节点的 Hash 值;
-
Merkle Tree 的 Tree 可以是任何形式的 Tree ,任何经典的 tree 构造算法都可以经过简单的修改应用到 Merkle Tree 上;
-
Merkle Tree 的 Branch Node 也可以存储数据,尽管大多数实现中只在 Leaf Node 上存储数据;
-
Merkle Tree 对单个数据的校验最多需要 O(h)O(h) 时间,其中 hh 为树高,如果树足够平衡,则验证单个节点的复杂度为 O(log(n))O(log(n)).
在 BitCoin 中,Merkle Tree 主要用来实现轻节点,轻节点只存 Top Hash,当轻节点要验证一笔交易时(比如上图中的 L4 ),则向存有全部数据的完全节点验证,完全节点将L4 到 root 的路径上的所有 node(1-1,1-0,1,0,Top Hash),轻节点对根据这条路径计算得到 Top Hash,如果计算得到的 Top Hash 与本地的 Top Hash 相等,则轻节点就可以相信完全节点传过来的数据。
在 Ethereum 中,Merkle Tree 除用来实现轻节点外,还用来实现增量存储。
MPT
为了能够支持高效的检索及动态的插入、删除、修改,Ethereum 使用 Trie 来构建 Merkle tree,Ethereum 将其命名为 Merkle Patricia Tree(MPT),其示意图如下:
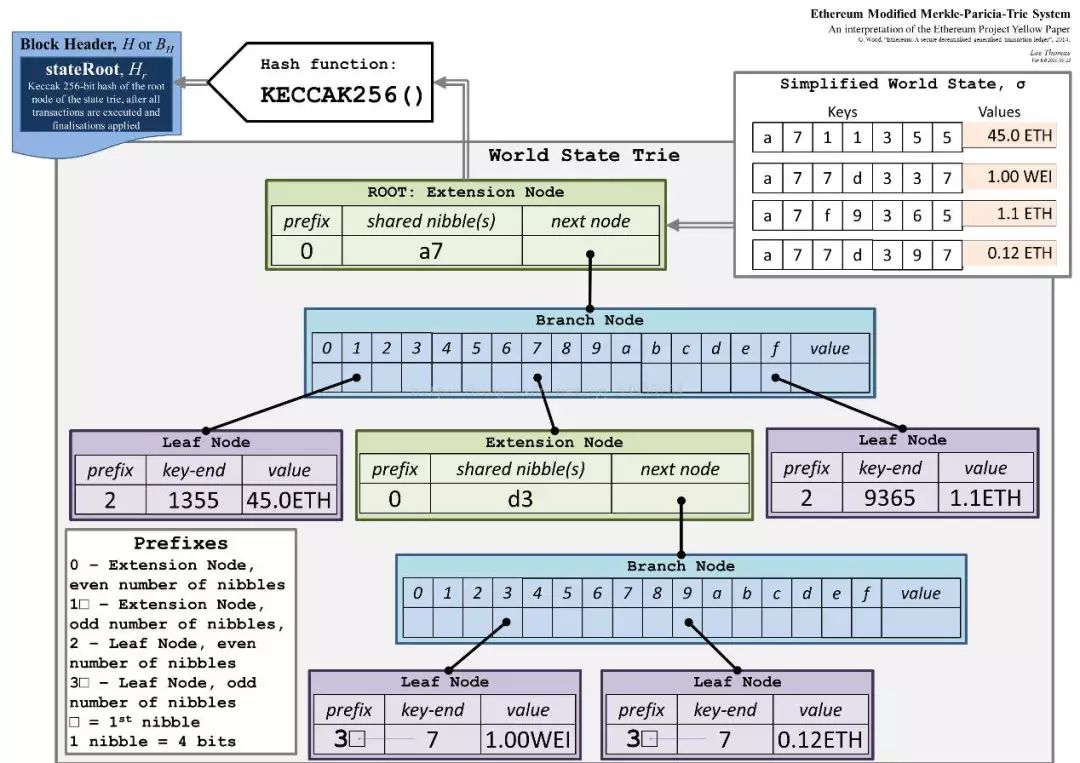
Ethereum 使用的是一棵 16 叉 Trie 树,并进行了路径压缩。可以将其理解为一棵普通的 Trie 树,只不过指向子节点的指针变成了子节点的 Hash。
2.1 Node类型
MPT 有三种类型的节点,分别是:Leaf Node、Branch Node、Extension Node。Leaf Node 由一个 Key 域(nibbles,key 的片段)及数据域组成;
Branch Node 由分支域(16个指向下一个节点的指针,这里的指针可以理解为 KV 数据库中的 Key)及数据域(如果存有数据,则此数据的 Key 是从根到达该 Node 所经过的所有 nibbles )组成;Extension Node 由 Key 域(Shared nibbles,这实际上是对路径进行压缩,否则路径的长度就是 key 的长度,在 Node 数量不多的情况下,树会非常的不平衡)及分支域(指向下一个 Branch Node 的指针)组成。
Parity 中 MPT 定义如下:
enum Node {
/// Empty node.
Empty,
/// A leaf node contains the end of a key and a value.
/// This key is encoded from a `NibbleSlice`, meaning it contains
/// a flag indicating it is a leaf.
Leaf(NodeKey, DBValue),
/// An extension contains a shared portion of a key and a child node.
/// The shared portion is encoded from a `NibbleSlice` meaning it contains
/// a flag indicating it is an extension.
/// The child node is always a branch.
Extension(NodeKey, NodeHandle),
/// A branch has up to 16 children and an optional value.
Branch(Box<[Option<NodeHandle>; 16]>, Option<DBValue>)
}
enum NodeHandle {
/// Loaded into memory.
InMemory(StorageHandle),
/// Either a hash or an inline node
Hash(H256),
}
注意此处的 NodeHandle ,我们可以只用 H256 来作为指向下一个节点的指针,这完全可行且符合协议,但是每次找子节点都要从数据库中查询势必会带来效率上的问题,Parity 采用了一个非常巧妙的办法,将查询过的 Node 都存放到内存中,下次需要找这些节点时直接用指针访问就好。当然,将其存到 DB 中时还是要将 InMemory(StorageHandle) 转化成 H256 格式,实际存储格式如下:
pub enum Node<'a> {
/// Null trie node; could be an empty root or an empty branch entry.
Empty,
/// Leaf node; has key slice and value. Value may not be empty.
Leaf(NibbleSlice<'a>, &'a [u8]),
/// Extension node; has key slice and node data. Data may not be null.
Extension(NibbleSlice<'a>, &'a [u8]),
/// Branch node; has array of 16 child nodes (each possibly null) and an optional immediate node data.
Branch([&'a [u8]; 16], Option<&'a [u8]>)
}
2.2 操作
除了最基本的增删改查操作以外,Parity 还有一个 commit 操作,该操作允许只有在调用 commit 时才重新计算Hash并写入数据库,这使得如果一个 node 被多次访问,这个 node 只重新计算一次 Hash,重新写入数据库一次。
commit 的另一个好处是在交易执行完之后再计算 Hash,这相当于做了路径聚合,去掉了重复无用的 Hash 计算,减少了 Hash 的计算量。目前 Parity 在每个交易执行完毕后都会调用 commit(),在我们的实现中将 commit 操作移到了块中所有交易完成以后,提高了效率。自 EIP98 以后,transaction 下的 state root 已经成了可选项,相信不久 Parity 也好把 commit 移到块中所有交易执行完之后。
/// Commit the in-memory changes to disk, freeing their storage and
/// updating the state root.
pub fn commit(&mut self) {
trace!(target: "trie", "Committing trie changes to db.");
// always kill all the nodes on death row.
trace!(target: "trie", "{:?} nodes to remove from db", self.death_row.len());
for hash in self.death_row.drain() {
self.db.remove(&hash);
}
let handle = match self.root_handle() {
NodeHandle::Hash(_) => return, // no changes necessary.
NodeHandle::InMemory(h) => h,
};
match self.storage.destroy(handle) {
Stored::New(node) => {
let root_rlp = node.into_rlp(|child, stream| self.commit_node(child, stream));
*self.root = self.db.insert(&root_rlp[..]);
self.hash_count += 1;
trace!(target: "trie", "root node rlp: {:?}", (&root_rlp[..]).pretty());
self.root_handle = NodeHandle::Hash(*self.root);
}
Stored::Cached(node, hash) => {
// probably won't happen, but update the root and move on.
*self.root = hash;
self.root_handle = NodeHandle::InMemory(self.storage.alloc(Stored::Cached(node, hash)));
}
}
}
/// commit a node, hashing it, committing it to the db,
/// and writing it to the rlp stream as necessary.
fn commit_node(&mut self, handle: NodeHandle, stream: &mut RlpStream) {
match handle {
NodeHandle::Hash(h) => stream.append(&h),
NodeHandle::InMemory(h) => match self.storage.destroy(h) {
Stored::Cached(_, h) => stream.append(&h),
Stored::New(node) => {
let node_rlp = node.into_rlp(|child, stream| self.commit_node(child, stream));
if node_rlp.len() >= 32 {
let hash = self.db.insert(&node_rlp[..]);
self.hash_count += 1;
stream.append(&hash)
} else {
stream.append_raw(&node_rlp, 1)
}
}
}
};
}
注:Node 在存入数据库之前都要先经过 RLP 序列化,Node 从数据库中取出时要先反序列化。
2.3 FatTrie & SecTrie
Parity 对上面的 TrieDB 进行了一层封装,分别是 SecTrie与 FatTrie。SecTrie 对传进来的 Key 做了一次 Sha3(),用 Sha3() 后的值作为 Key,这样做的原因是:Trie 并不是一棵平衡树,攻击者可以构造一棵极端不平衡的树来进行 DDos 攻击,用 Sh3() 后的值做 Key,这极大增加了攻击难度,使构造极端不平衡的树几乎不可能。FatTrie 除了对 Key 做 Sha3() 外,还额外将 Sha3() 前的 Key 存了下来。
Merkle AVL+Tree
由于 Sha3 运算的开销并不低(约 15Cycles/byte15Cycles/byte),为了提高效率,我们希望在每次更新树时能够计算 Sha3 的数量最少,而更新一个节点所需要重新计算的 Sha3 量约为 mlogmnmlogmn,其中 mm 为分支数,故当 m=2m=2 时,Sha3 的计算量最小。又 AVL Tree 的平衡性更好(尽管这意味着更多的旋转操作,幸运的是旋转操作并不增加 Sha3 计算),因此选用 AVL Tree 来构建 Merkle Tree 似乎是一个不错的选择,我们简称之为 MAT。
3.1 Node 类型
为了简化操作,我们只在叶子节点存放数据(这样可以减少重新计算 Sha3 的量),MAT 有两种类型的 Node:Branch Node 和 Leaf Node:
/// Node types in the AVL.
#[derive(Debug)]
enum Node {
/// Empty node.
Empty,
/// A leaf node contains a key and a value.
Leaf(NodeKey, DBValue),
/// A branch has up to 2 children and a key.
Branch(u32, NodeKey, Box<[Option<NodeHandle>; 2]>),
}
Leaf Node 由 Key 域(不同于 MPT,这里存了完整的 key)及数据域组成,Branch Node 由 Key 域(这里仍然存储的是完整的 Key,其 Key 与其子树中最左边的叶子节点的 Key 相同)及分支域(两个分支)组成。
3.2 操作
MAT 支持的操作同 MPT,不同的是为了保持树的平衡,会有 LL、LR、RR、RL 四种旋转操作。
对比
两种树更新一个 node 时所需的 Sha3 计算量对比如下图所示:
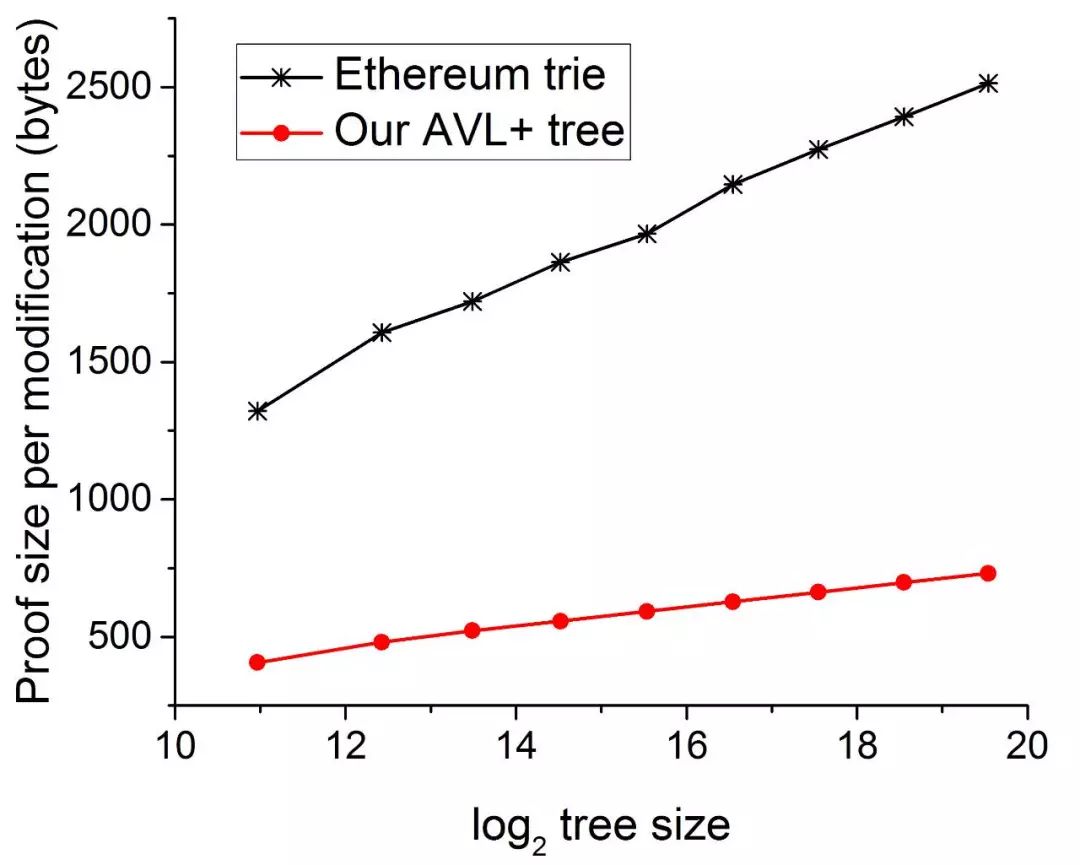
测试发现,当 node 数在 1000,0001000,000 时,MPT 的平均路径长度为 7,MAT 的平均路径长度为 20,可以推算 MPT 的 Sha3 计算量为16×7=11216×7=112,MAT 的 Sha3 计算量为 2×20=402×20=40,这与上图数据吻合。
4.1 MPT存在的问题
-
trie 并不是平衡树,这意味着攻击者可以通过特殊的数据构造一棵很高的树,从而进行拒绝服务攻击。(实际上这很难进行,因为在 Ethereum 中 Key 是经过 Sha3 后的值,想找到特定值的 Sha3 是困难的。);
-
内存占用率高。每个 Branch Node 都 16 个子节点指针,大多数情况下其子节点的数量并不多;
-
不易于编码。虽然 MPT 易于理解,但是编写却非常复杂,MPT 的代码量比 MAT 要高出许多。
4.2 AVL+ 存在的问题
-
不同的插入顺序得到的 AVL Tree 并不相同,这意味着不能像 MPT 那样将 DB 理解为内存模型,合约设计者必须意识到不同的写入顺序将带来不同的结果,也就是说,AVL 天然的不支持合约内的并行;
-
每个 Node 节点都存有完整的 Key,Key 的存储开销要比 MPT 大;
-
每个 Key 的大小是 256bit,Key最长可能要做 32 次 u8 比较,但从概率上来讲,大部分 Node 会在前几次比较就得出结果。
-
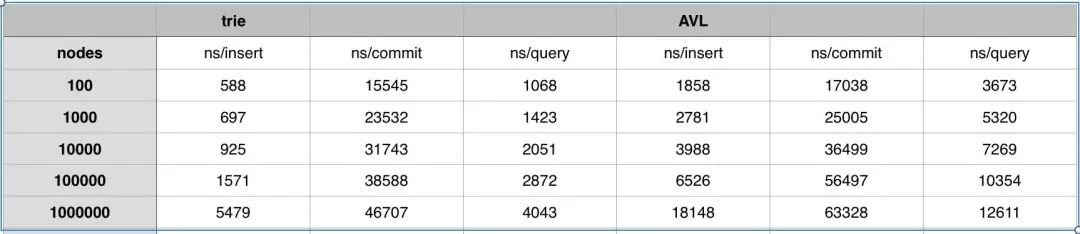
由于 AVL 是二叉树,这意味着 AVL 的树高要比 Trie 树高,也就是说 AVL 操作 DB 的次数要比 Trie 树多,从而 IO 开销要比 Trie 树高。
由于 IO 开销,实际性能 AVL 要比 Trie 差:
秘猿科技 repo:https://github.com/cryptape
连接开发者与运营方的合作平台 CITAHub:https://www.citahub.com/
有任何技术问题可以在论坛讨论:https://talk.nervos.org

相关推荐
GEM^2-Tree: A Gas-Efficient Structure for Authenticated Range Queries in Blockchain Ce Zhang, Cheng Xu, Jianliang Xu, Yuzhe Tang,et al.GEM^2-Tree: A Gas-Efficient Structure for Authenticated Range ...
- **抵抗主动攻击**:AD-ASGKA 能够有效抵御中间人攻击(man-in-the-middle attack)和其他形式的主动攻击。 - **防止密钥泄露**:即使某些成员的私钥被泄露,也不会影响到其他成员的安全性。 - **前向安全性**:即便...
"acts_as_authenticated" 是一个经典的Ruby on Rails插件,它为Rails应用提供了用户认证功能。在Rails框架中,用户认证通常涉及验证用户身份、管理会话以及处理登录和登出等操作。acts_as_authenticated插件简化了这...
「日志审计」Modeling_Memory_Faults_in_Signature_and_Authenticated_Encryption_Schemes - 身份管理 访问管理 基础架构安全 应用安全 WEB应用防火墙 安全测试
#### 概述 ...作为一种个人隐私保护的有效手段,APAKE近年来受到了广泛关注。然而,大多数现有的APAKE协议都是基于随机预言模型设计的。本研究提出了一种在标准模型下具有可证明安全性的纯密码APAKE协议(称为APAKE-S...
标题提及的“Symmetric Key Authenticated Key Exchange”(对称密钥认证密钥交换,简称SAKE)是一种针对低资源设备设计的安全协议,旨在解决资源受限设备上的通信安全问题,尤其是在需要双向认证、密钥协商和前向...
"authenticated_data:玩经过身份验证的数据结构" 这个标题指出我们要讨论的是一个关于数据验证的特定概念,特别是在编程语言Idris 2的上下文中。"玩"这个词在这里可能意味着探索或实验,暗示我们将深入研究如何在...
【标题】"Authenticated User Community-开源" 在信息技术领域,开源软件是一个重要的概念,它指的是那些源代码可以被公众查看、使用、修改和分发的软件。"Authenticated User Community"(AUC)是一个专为此目标而...
标题中的"基于ASP.NET+AJAX+FormsAuthentication实现的authenticated users检索"指的是一项使用了ASP.NET、AJAX以及FormsAuthentication技术来实现用户身份验证和检索功能的Web应用程序。这个应用允许只对已验证...
密码认证密钥交换(Password-authenticated key exchange, PAKE)协议允许两个拥有密码的实体进行相互认证,并建立一个用于后续通信的会话密钥。PAKE协议的优点在于使用了低熵、易于人类记忆的密码,这避免了在认证...
### 两因素认证密钥交换协议在云计算中的安全实现 #### 概述 随着云计算技术的迅速发展,用户越来越依赖云服务来存储和处理数据。然而,在享受便捷服务的同时,如何确保数据的安全传输与身份验证成为了关键问题。...
在LDAP(轻量级目录访问协议)环境中,配置允许经过身份验证的用户浏览和阅读条目是管理员确保安全访问控制的重要任务。默认情况下,如果启用了访问控制系统,只有管理员能够浏览目录信息树(DIT)。...
Causes the next filter in the chain to be invoked, or if the calling filter is the last filter in the chain, causes the resource at the end of the chain to be invoked. doFilter(ServletRequest, ...
Who Is Being Authenticated? Section 9.5. Passwords as Cryptographic Keys Section 9.6. Eavesdropping and Server Database Reading Section 9.7. Trusted Intermediaries Section 9.8. Session Key ...
Cross-domain password-based authenticated key exchange (PAKE) protocols have been studied for many years. However, these protocols are mainly focusing on multi-participant within a single domain in an...
In CT-RSA 2007, Jarecki, Kim, and Tsudik introduced the notion of affiliation-hiding authenticated group key agreement (AH-AGKA) protocols and presented two concrete AH-AGKA protocols. In this paper, ...
530 5.7.1 Client was not authenticated 经过搜索, 找到解决方案如下. 开启Exchange Management Shell, 输入如下命令: Set-ReceiveConnector "Default <Servername>" -permissiongroups:"ExchangeUsers,...
### 分析网络日志文章中人们的关注点 #### 摘要与背景 本文提出了一种分析网络日志(Weblog)文章中人们关注点的系统——KANSHIN。该系统通过收集大量的日语、汉语及韩语的网络日志文章来分析不同语言社区的人们对...
利用Nagios-XI-5.7.X远程代码执行RCE身份验证 Nagios XI 5.7.X-远程执行代码RCE(已认证)