1. 引言
有向无环图(Directed Acyclic Graph, DAG)是有向图的一种,字面意思的理解就是图中没有环。常常被用来表示事件之间的驱动依赖关系,管理任务之间的调度。拓扑排序是对DAG的顶点进行排序,使得对每一条有向边(u, v),均有u(在排序记录中)比v先出现。亦可理解为对某点v而言,只有当v的所有源点均出现了,v才能出现。
下图给出有向无环图的拓扑排序:
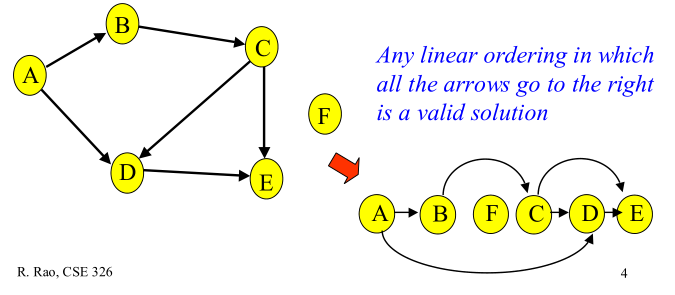
下图给出的顶点排序不是拓扑排序,因为顶点D的邻接点E比其先出现:
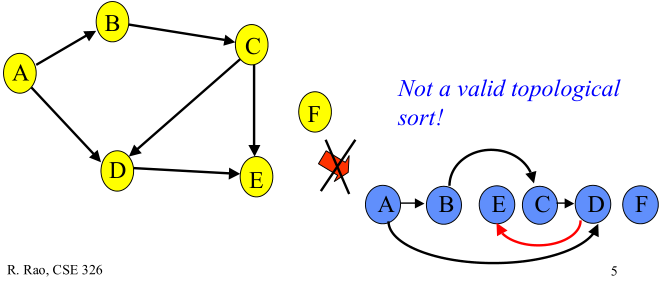
2. 算法原理与实现
拓扑排序的实现算法有两种:入度表、DFS,其时间复杂度均为O(V+E)O(V+E)。
入度表
对于DAG的拓扑排序,显而易见的办法:
- 找出图中0入度的顶点;
- 依次在图中删除这些顶点,删除后再找出0入度的顶点;
- 然后再删除……再找出……
- 直至删除所有顶点,即完成拓扑排序
为了保存0入度的顶点,我们采用数据结构栈(亦可用队列);算法的可视化可参看这里。
图用邻接表(adjacency list)表示,用数组inDegreeArray[]记录结点的入度变化情况。C实现:
// get in-degree array
int *getInDegree(Graph *g) {
int *inDegreeArray = (int *) malloc(g->V * sizeof(int));
memset(inDegreeArray, 0, g->V * sizeof(int));
int i;
AdjListNode *pCrawl;
for(i = 0; i < g->V; i++) {
pCrawl = g->array[i].head;
while(pCrawl) {
inDegreeArray[pCrawl->dest]++;
pCrawl = pCrawl->next;
}
}
return inDegreeArray;
}
// topological sort function
void topologicalSort(Graph *g) {
int *inDegreeArray = getInDegree(g);
Stack *zeroInDegree = initStack();
int i;
for(i = 0; i < g->V; i++) {
if(inDegreeArray[i] == 0)
push(i, zeroInDegree);
}
printf("topological sorted order\n");
AdjListNode *pCrawl;
while(!isEmpty(zeroInDegree)) {
i = pop(zeroInDegree);
printf("vertex %d\n", i);
pCrawl = g->array[i].head;
while(pCrawl) {
inDegreeArray[pCrawl->dest]--;
if(inDegreeArray[pCrawl->dest] == 0)
push(pCrawl->dest, zeroInDegree);
pCrawl = pCrawl->next;
}
}
}时间复杂度:得到inDegreeArray[]数组的复杂度为O(V+E)O(V+E);顶点进栈出栈,其复杂度为O(V)O(V);删除顶点后将邻接点的入度减1,其复杂度为O(E)O(E);整个算法的复杂度为O(V+E)O(V+E)。
DFS
在DFS中,依次打印所遍历到的顶点;而在拓扑排序时,顶点必须比其邻接点先出现。在下图中,顶点5比顶点0先出现,顶点4比顶点1先出现。
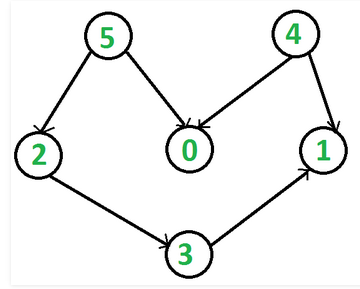
在DFS实现拓扑排序时,用栈来保存拓扑排序的顶点序列;并且保证在某顶点入栈前,其所有邻接点已入栈。DFS版拓扑排序的可视化参看这里。
C实现:
/* recursive DFS function to traverse the graph,
* the graph is represented by adjacency list
*/
void dfs(int u, Graph *g, int *visit, Stack *s) {
visit[u] = 1;
AdjListNode *pCrawl = g->array[u].head;
while(pCrawl) {
if(!visit[pCrawl->dest])
dfs(pCrawl->dest, g, visit, s);
pCrawl = pCrawl->next;
}
push(u, s);
}
// the topological sort function
void topologicalSort(Graph *g) {
int *visit = (int *) malloc(g->V * sizeof(int));
memset(visit, 0, g->V * sizeof(int));
Stack *s = initStack();
int i;
for(i = 0; i < g->V; i++) {
if(!visit[i]) dfs(i, g, visit, s);
}
// the order of stack element is the sorted order
while(!isEmpty(s)) {
printf("vertex %d\n", pop(s));
}
}时间复杂度:应与DFS相同,为O(V+E)O(V+E)。
完整代码在Github。





相关推荐
图的拓扑排序和有向无环图(Directed Acyclic Graph, DAG)的判断是图论中的基础概念,广泛应用于计算机科学的多个领域,如任务调度、编译器设计等。拓扑排序是对有向无环图进行线性排列的一种方式,而DAG的环检测则...
总之,有向无环图的拓扑排序与环检测是图论中的基本问题,对于理解和优化依赖关系的系统具有重要意义。实际应用中,这类算法常用于编译器的依赖分析、项目管理的任务调度等领域。通过深入理解并实践这些算法,我们...
拓扑排序是对有向无环图(DAG,Directed Acyclic Graph)进行的一种线性排序,其结果是使得对于图中每条有向边 (u, v),节点 u 都在节点 v 的前面。如果一个有向图存在环,则无法进行拓扑排序,因为环会导致排序的不...
总结来说,拓扑排序不仅可以用来有序地组织有向无环图的节点,还可以作为一个有效的工具来检测有向图中是否含有环。通过DFS或BFS策略,可以在实践中快速判断一个有向图是否存在环,这对于理解和处理有向图结构的算法...
拓扑排序(Topological Sort)是一种线性排序算法,它只适用于有向无环图(DAG)。这种排序方式能够将图中的顶点排成一个线性的序列,使得对于任意一对顶点u和v,如果图中存在从u到v的路径,则u在序列中出现在v之前...
有向图的拓扑排序是图论中的一个重要概念,它主要应用于有向无环图(DAG,Directed Acyclic Graph)。在数据结构的学习中,拓扑排序是对有向图节点的一种线性排序,使得对于图中的每一条有向边 `(u, v)`,节点 `u` ...
拓扑排序是图论中的一个重要概念,主要应用于有向无环图(DAG,Directed Acyclic Graph)。在这样的图中,节点之间的关系是有方向性的,而拓扑排序就是找到一个线性的顺序,使得对于每一条边 (u, v),节点 u 都在这...
拓扑排序是图论中的一个重要概念,特别是在有向无环图(DAG,Directed Acyclic Graph)处理中显得尤为关键。这种算法的目标是为图中的节点找到一个线性顺序,使得对于每一条从节点u到节点v的有向边,u都在v之前出现...
【拓扑排序】是图论中的一个重要概念,用于对有向无环图(DAG,Directed Acyclic Graph)进行线性排序。在这个过程中,我们尝试按照一定的顺序排列顶点,使得对于图中的每一条有向边 (u, v),顶点 u 总是出现在顶点 ...
拓扑排序是图论中的一个重要概念,主要应用于有向无环图(DAG,Directed Acyclic Graph)。在计算机科学中,特别是在数据结构和算法领域,拓扑排序常常用于解决依赖关系的排序问题,例如课程安排、任务调度等场景。...
拓扑排序则是图论中一个实用且基础的概念,它主要用于有向无环图(DAG,Directed Acyclic Graph)的排序问题。在本实验代码中,我们将深入探讨拓扑排序的原理、实现方法及其应用。 拓扑排序是对有向无环图的顶点...
拓扑排序是图论中的一个重要概念,特别是在有向无环图(DAG,Directed Acyclic Graph)处理中非常实用。VC++是一种强大的编程语言,它提供了丰富的库支持来进行各种算法的实现,包括拓扑排序。在本教程中,我们将...
在“图论- AOV 网与拓扑排序.pdf”文档中,你可能会学到如何构建AOV网络,理解有向无环图的概念,学习拓扑排序的算法实现,以及如何在实际问题中运用这些理论。通过阅读这份资料,你可以深化对图论的理解,掌握解决...
拓扑排序是图论中的一个重要概念,特别是在有向无环图(DAG)处理中非常有用。它是对有向无环图的顶点的一种线性排序,使得对于每一条有向边 (u, v),顶点 u 都在这个排序中出现在顶点 v 之前。拓扑排序的特性使得它在...
拓扑排序是图论中的一个重要概念,主要用于有向无环图(DAG,Directed Acyclic Graph)。在C语言中实现拓扑排序算法,可以帮助我们理解数据结构与算法的基础,并为解决实际问题提供工具。下面将详细阐述拓扑排序的...
图的拓扑排序是数据结构领域中图论的一部分,它主要应用于有向无环图(DAG,Directed Acyclic Graph)。在这样的图中,拓扑排序是对所有节点的一种线性排列,使得对于每一条有向边 (u, v),节点 u 在排列中都出现在...
拓扑排序是图论中的一个重要概念,特别是在有向无环图(DAG,Directed Acyclic Graph)中。在计算机科学中,它常用于解决任务调度、依赖关系分析等问题。本篇将详细介绍拓扑排序的概念、算法及其在C++中的实现。 ##...
拓扑排序是图论中的一个重要概念,特别是在有向无环图(DAG,Directed Acyclic Graph)中。在计算机科学中,数据结构和算法的设计往往涉及到拓扑排序的应用,例如在任务调度、编译器的依赖关系分析以及网络流量优化...
拓扑排序是图论中的一个重要概念,主要应用于有向无环图(DAG,Directed Acyclic Graph)。在这样的图中,拓扑排序可以将所有节点按照没有前驱(入度为0)到有前驱的顺序排列。这种排序保证了对于任意的边 (u, v),...