1 时间序列与时间序列分析
在生产和科学研究中,对某一个或者一组变量 进行观察测量,将在一系列时刻 所得到的离散数字组成的序列集合,称之为时间序列。
时间序列分析是根据系统观察得到的时间序列数据,通过曲线拟合和参数估计来建立数学模型的理论和方法。时间序列分析常用于国民宏观经济控制、市场潜力预测、气象预测、农作物害虫灾害预报等各个方面。
2 时间序列建模基本步骤
- 获取被观测系统时间序列数据;
- 对数据绘图,观测是否为平稳时间序列;对于非平稳时间序列要先进行d阶差分运算,化为平稳时间序列;
- 经过第二步处理,已经得到平稳时间序列。要对平稳时间序列分别求得其自相关系数ACF 和偏自相关系数PACF ,通过对自相关图和偏自相关图的分析,得到最佳的阶层 p 和阶数 q
- 由以上得到的 ,得到ARIMA模型。然后开始对得到的模型进行模型检验。
3 ARIMA实战解剖
原理大概清楚,实践却还是会有诸多问题。相比较R语言,Python在做时间序列分析的资料相对少很多。下面就通过Python语言详细解析后三个步骤的实现过程。
文中使用到这些基础库: 。 对其调用如下
-
from __future__ import print_function
-
import pandas as pd
-
import numpy as np
-
from scipy import stats
-
import matplotlib.pyplot as plt
-
import statsmodels.api as sm
-
from statsmodels.graphics.api import qqplot
3.1 获取数据
这里我们使用一个具有周期性的测试数据,进行分析。
数据如下:
dta=[10930,10318,10595,10972,7706,6756,9092,10551,9722,10913,11151,8186,6422,
6337,11649,11652,10310,12043,7937,6476,9662,9570,9981,9331,9449,6773,6304,9355,
10477,10148,10395,11261,8713,7299,10424,10795,11069,11602,11427,9095,7707,10767,
12136,12812,12006,12528,10329,7818,11719,11683,12603,11495,13670,11337,10232,
13261,13230,15535,16837,19598,14823,11622,19391,18177,19994,14723,15694,13248,
9543,12872,13101,15053,12619,13749,10228,9725,14729,12518,14564,15085,14722,
11999,9390,13481,14795,15845,15271,14686,11054,10395]
-
dta=pd.Series(dta)
-
dta.index = pd.Index(sm.tsa.datetools.dates_from_range('2001','2100'))
-
dta.plot(figsize=(12,8))
3.2 时间序列的差分
ARIMA 模型对时间序列的要求是平稳型。因此,当你得到一个非平稳的时间序列时,首先要做的即是做时间序列的差分,直到得到一个平稳时间序列。如果你对时间序列做d次差分才能得到一个平稳序列,那么可以使用ARIMA(p,d,q)模型,其中d是差分次数。
-
fig = plt.figure(figsize=(12,8))
-
ax1= fig.add_subplot(111)
-
diff1 = dta.diff(1)
-
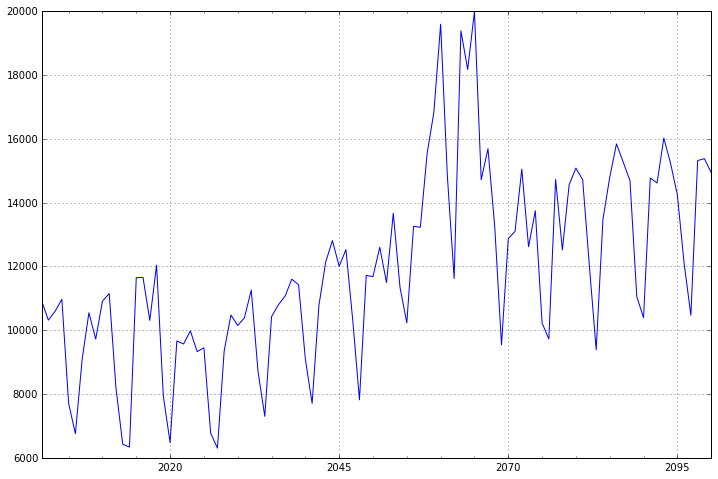
diff1.plot(ax=ax1)
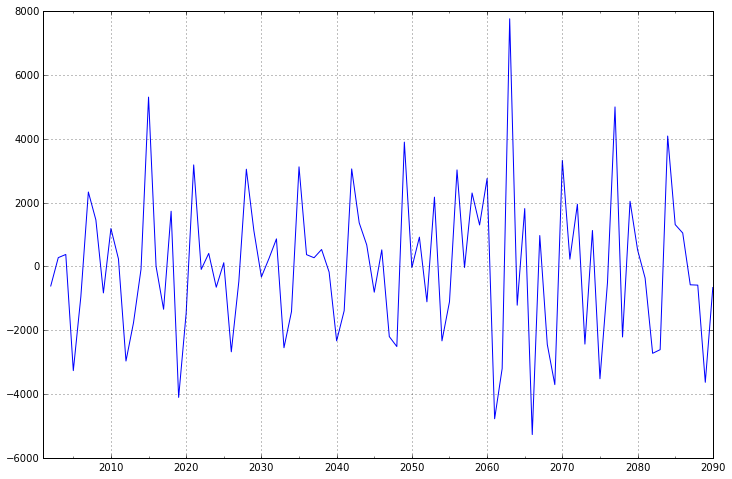
一阶差分的时间序列的均值和方差已经基本平稳,不过我们还是可以比较一下二阶差分的效果
-
fig = plt.figure(figsize=(12,8))
-
ax2= fig.add_subplot(111)
-
diff2 = dta.diff(2)
-
diff2.plot(ax=ax2)
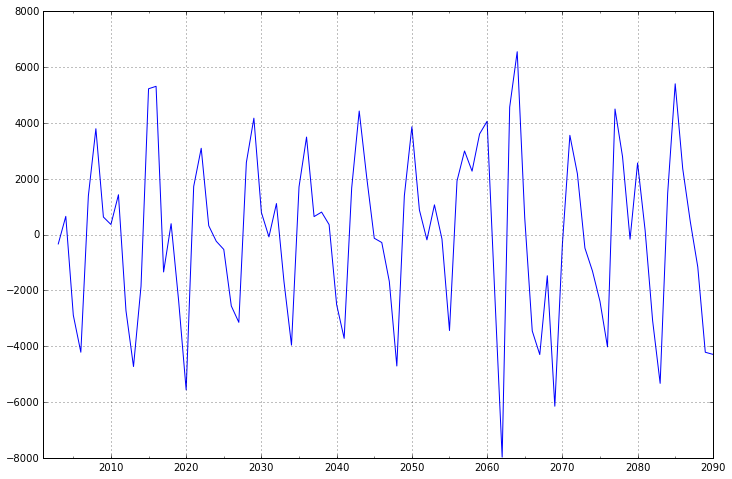
可以看出二阶差分后的时间序列与一阶差分相差不大,并且二者随着时间推移,时间序列的均值和方差保持不变。因此可以将差分次数d设置为1。
其实还有针对平稳的检验,叫“ADF单位根平稳型检验”,以后再更。
3.3 合适的
现在我们已经得到一个平稳的时间序列,接来下就是选择合适的ARIMA模型,即ARIMA模型中合适的。
第一步我们要先检查平稳时间序列的自相关图和偏自相关图。
-
dta= dta.diff(1)#我们已经知道要使用一阶差分的时间序列,之前判断差分的程序可以注释掉
-
fig = plt.figure(figsize=(12,8))
-
ax1=fig.add_subplot(211)
-
fig = sm.graphics.tsa.plot_acf(dta,lags=40,ax=ax1)
-
ax2 = fig.add_subplot(212)
-
fig = sm.graphics.tsa.plot_pacf(dta,lags=40,ax=ax2)
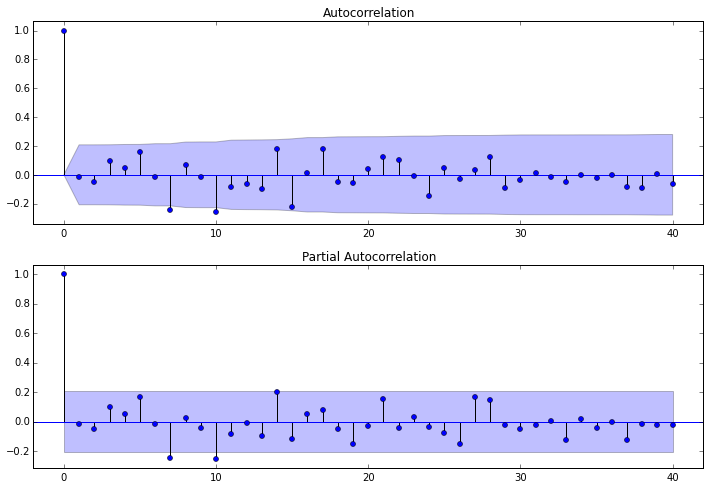
其中lags 表示滞后的阶数,以上分别得到acf 图和pacf 图 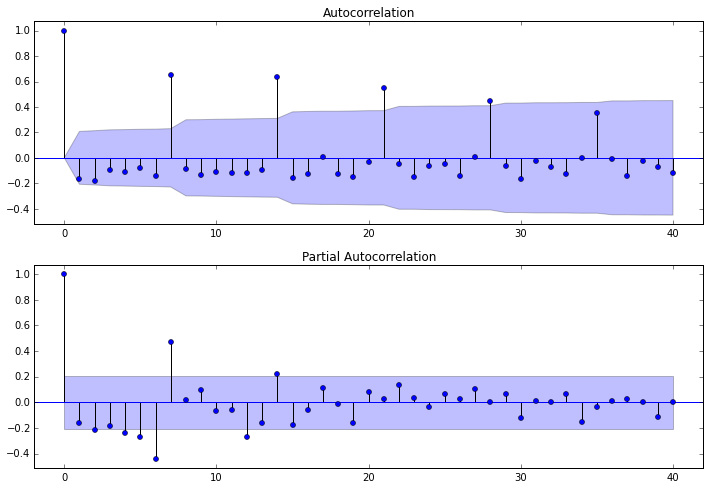
通过两图观察得到:
* 自相关图显示滞后有三个阶超出了置信边界;
* 偏相关图显示在滞后1至7阶(lags 1,2,…,7)时的偏自相关系数超出了置信边界,从lag 7之后偏自相关系数值缩小至0
则有以下模型可以供选择:
1. ARMA(0,1)模型:即自相关图在滞后1阶之后缩小为0,且偏自相关缩小至0,则是一个阶数q=1的移动平均模型;
2. ARMA(7,0)模型:即偏自相关图在滞后7阶之后缩小为0,且自相关缩小至0,则是一个阶层p=3的自回归模型;
3. ARMA(7,1)模型:即使得自相关和偏自相关都缩小至零。则是一个混合模型。
4. …还可以有其他供选择的模型
现在有以上这么多可供选择的模型,我们通常采用ARMA模型的AIC法则。我们知道:增加自由参数的数目提高了拟合的优良性,AIC鼓励数据拟合的优良性但是尽量避免出现过度拟合(Overfitting)的情况。所以优先考虑的模型应是AIC值最小的那一个。赤池信息准则的方法是寻找可以最好地解释数据但包含最少自由参数的模型。不仅仅包括AIC准则,目前选择模型常用如下准则:
* AIC=-2 ln(L) + 2 k 中文名字:赤池信息量 akaike information criterion
* BIC=-2 ln(L) + ln(n)*k 中文名字:贝叶斯信息量 bayesian information criterion
* HQ=-2 ln(L) + ln(ln(n))*k hannan-quinn criterion
构造这些统计量所遵循的统计思想是一致的,就是在考虑拟合残差的同时,依自变量个数施加“惩罚”。但要注意的是,这些准则不能说明某一个模型的精确度,也即是说,对于三个模型A,B,C,我们能够判断出C模型是最好的,但不能保证C模型能够很好地刻画数据,因为有可能三个模型都是糟糕的。
-
arma_mod20 = sm.tsa.ARMA(dta,(7,0)).fit()
-
print(arma_mod20.aic,arma_mod20.bic,arma_mod20.hqic)
-
arma_mod30 = sm.tsa.ARMA(dta,(0,1)).fit()
-
print(arma_mod30.aic,arma_mod30.bic,arma_mod30.hqic)
-
arma_mod40 = sm.tsa.ARMA(dta,(7,1)).fit()
-
print(arma_mod40.aic,arma_mod40.bic,arma_mod40.hqic)
-
arma_mod50 = sm.tsa.ARMA(dta,(8,0)).fit()
-
print(arma_mod50.aic,arma_mod50.bic,arma_mod50.hqic)
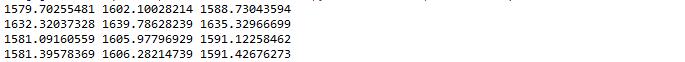
可以看到ARMA(7,0)的aic,bic,hqic均最小,因此是最佳模型。
3.4 模型检验
在指数平滑模型下,观察ARIMA模型的残差是否是平均值为0且方差为常数的正态分布(服从零均值、方差不变的正态分布),同时也要观察连续残差是否(自)相关。
3.4.1 我们对ARMA(7,0)模型所产生的残差做自相关图
-
fig = plt.figure(figsize=(12,8))
-
ax1 = fig.add_subplot(211)
-
fig = sm.graphics.tsa.plot_acf(resid.values.squeeze(), lags=40, ax=ax1)
-
ax2 = fig.add_subplot(212)
-
fig = sm.graphics.tsa.plot_pacf(resid, lags=40, ax=ax2)
3.4.2 做D-W检验
德宾-沃森(Durbin-Watson)检验。德宾-沃森检验,简称D-W检验,是目前检验自相关性最常用的方法,但它只使用于检验一阶自相关性。因为自相关系数ρ的值介于-1和1之间,所以 0≤DW≤4。并且DW=O=>ρ=1 即存在正自相关性
DW=4<=>ρ=-1 即存在负自相关性
DW=2<=>ρ=0 即不存在(一阶)自相关性
因此,当DW值显著的接近于O或4时,则存在自相关性,而接近于2时,则不存在(一阶)自相关性。这样只要知道DW统计量的概率分布,在给定的显著水平下,根据临界值的位置就可以对原假设H0进行检验。
print(sm.stats.durbin_watson(arma_mod20.resid.values))
检验结果是2.02424743723,说明不存在自相关性。
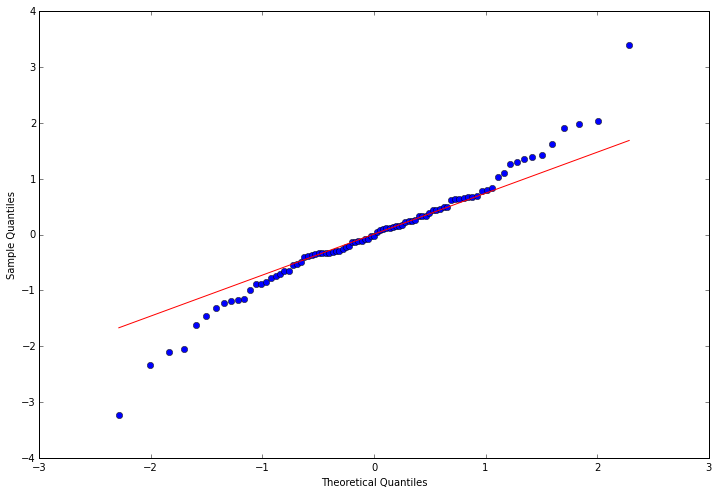
3.4.3 观察是否符合正态分布
这里使用QQ图,它用于直观验证一组数据是否来自某个分布,或者验证某两组数据是否来自同一(族)分布。在教学和软件中常用的是检验数据是否来自于正态分布。QQ图细节,下次再更。
-
resid = arma_mod20.resid#残差
-
fig = plt.figure(figsize=(12,8))
-
ax = fig.add_subplot(111)
-
fig = qqplot(resid, line='q', ax=ax, fit=True)
3.4.4 Ljung-Box检验
Ljung-Box test是对randomness的检验,或者说是对时间序列是否存在滞后相关的一种统计检验。对于滞后相关的检验,我们常常采用的方法还包括计算ACF和PCAF并观察其图像,但是无论是ACF还是PACF都仅仅考虑是否存在某一特定滞后阶数的相关。LB检验则是基于一系列滞后阶数,判断序列总体的相关性或者说随机性是否存在。
时间序列中一个最基本的模型就是高斯白噪声序列。而对于ARIMA模型,其残差被假定为高斯白噪声序列,所以当我们用ARIMA模型去拟合数据时,拟合后我们要对残差的估计序列进行LB检验,判断其是否是高斯白噪声,如果不是,那么就说明ARIMA模型也许并不是一个适合样本的模型。
-
r,q,p = sm.tsa.acf(resid.values.squeeze(), qstat=True)
-
data = np.c_[range(1,41), r[1:], q, p]
-
table = pd.DataFrame(data, columns=['lag', "AC", "Q", "Prob(>Q)"])
-
print(table.set_index('lag'))
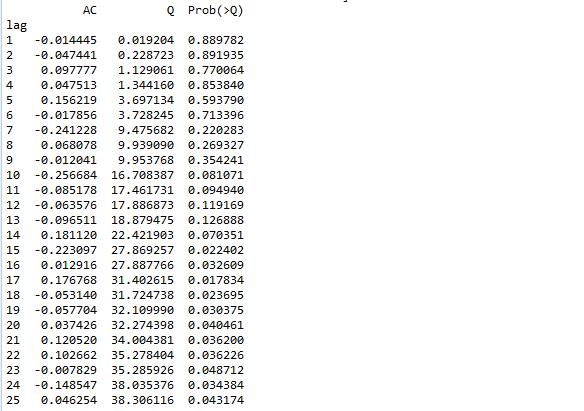
检验的结果就是看最后一列前十二行的检验概率(一般观察滞后1~12阶),如果检验概率小于给定的显著性水平,比如0.05、0.10等就拒绝原假设,其原假设是相关系数为零。就结果来看,如果取显著性水平为0.05,那么相关系数与零没有显著差异,即为白噪声序列。
3.5 模型预测
模型确定之后,就可以开始进行预测了,我们对未来十年的数据进行预测。
-
predict_sunspots = arma_mod20.predict('2090', '2100', dynamic=True)
-
print(predict_sunspots)
-
fig, ax = plt.subplots(figsize=(12, 8))
-
ax = dta.ix['2001':].plot(ax=ax)
-
predict_sunspots.plot(ax=ax)
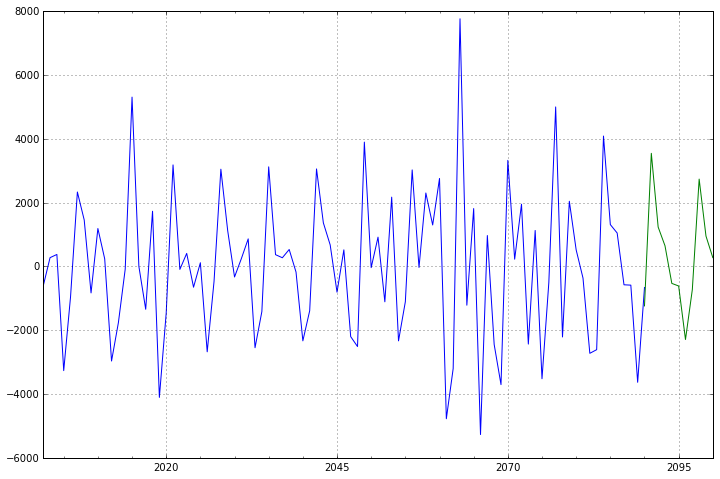
前面90个数据为测试数据,最后10个为预测数据;从图形来,预测结果较为合理。至此,本案例的时间序列分析也就结束了。





相关推荐
【项目实战】基于Python实现时间序列分析建模(ARIMA模型)项目实战 内容包括: 资料说明:包括数据集+源代码+PDF文档说明+代码视频讲解。 资料内容包括: 1)项目背景; 2)数据收集; 3)数预处理; 4)RBF神经网络...
在Python中,有许多强大的库,如`pandas`、`statsmodels`和`forecast`,可以帮助我们进行时间序列分析与预测。本文将深入探讨时间序列分析的常用算法,并以Python为例,展示如何实现这些算法。 首先,我们要理解...
使用ARIMA模型进行时间序列数据分析 编程语言:python 代码编辑器:jupyter notebook 适合想了解ARIMA模型的大致流程以及代码实现的朋友
在时间序列分析中,ARIMA(自回归整合滑动平均模型)是一种常用的方法,尤其在预测未来的趋势和波动方面。本资源围绕“ZIP_danger1t1_turnazi_arima_python时间序列预测_ARIMA预测”这一主题,提供了一个使用Python...
时间序列分析之ARIMA上手-Python-附件资源
ARIMA是时间序列分析的经典模型,由自回归(AR)、差分(I)和滑动平均(MA)三个部分组成。AR部分考虑了历史值之间的线性关系,I用于处理非平稳时间序列,使之变为平稳,MA则考虑了随机误差项的影响。在电力负荷...
本压缩包"Python时间序列分析测试数据及代码.zip"包含了相关测试数据和实际的Python代码,帮助我们深入理解和实践这一主题。 首先,我们要了解什么是时间序列分析。时间序列是一组按时间顺序排列的数据点,每个数据...
arima,ARIMA预测模型预测销量ARIMA.py :预测模型Result.py:打印预测值
本资料《通过Python进行时间序列的分析与预测》由Changquan Huang和Alla Petukhina共同撰写,旨在为读者提供应用Python进行时间序列分析和预测的全面指导。 首先,了解时间序列的基本概念至关重要。时间序列是由...
本讲义主要探讨了两种常用的时间序列预测模型:ARIMA(自回归积分滑动平均模型)和LSTM(长短期记忆网络),并结合Python编程实践进行了深入讲解。 ARIMA模型是基于线性统计模型的时间序列预测方法,它结合了自回归...
首先,我们需要了解时间序列分析的基本概念。时间序列是指按照特定时间顺序排列的一系列数值,它反映了某个变量在不同时间点上的变化情况。在Python中,常用的库如Pandas和NumPy提供了处理和分析时间序列数据的强大...
适用人群:时间序列分析初学者和从业者,特别是希望深入了解ARIMA模型及其应用的技术人士。 使用场景及目标:本文章旨在帮助读者掌握ARIMA模型的基础知识,并能够将其应用于具体的时间序列预测任务中,如经济预测、...
在Python中,时间序列分析是一种处理按时间顺序排列的数据集的方法,广泛应用于金融、气象学、经济学、社会科学以及工程等领域。本章节将深入探讨Python在时间序列分析中的应用,特别是如何利用Python强大的库如...
【基于Python的时间序列分析在降雨量预测中的应用】 时间序列分析是一种统计技术,用于分析和预测按时间顺序排列的数据序列。在本论文中,作者利用Python编程语言和时间序列分析来构建一个雨量预测系统,旨在提高对...
本示例将详细介绍如何使用Python实现ARIMA和其扩展版SARIMA(季节性ARIMA)进行时间序列分析。 首先,我们需要导入必要的库,包括`pandas`用于数据处理,`matplotlib`用于数据可视化,以及`statsmodels`中的`tsa`...
Python之所以被广泛用于时间序列分析,是因为其丰富的库和简洁的语法。尽管SAS和R在实际工作中更常见,但Python的pandas库提供了高效处理时间序列数据的能力。此外,statsmodels库中的tsa模块虽然不如SAS和R强大,但...
在数据分析和预测领域,时间序列分析是一种常用的技术,特别是在销售预测、股票市场预测以及气象预报等方面。Python作为数据科学的主要工具,提供了强大的库来处理时间序列数据,如pandas、matplotlib以及统计建模库...
ARIMA(自回归整合滑动平均模型)是时间序列分析中的一种重要模型,结合了自回归(AR)、差分(I)和移动平均(MA)三个部分。ARIMA模型能够处理非平稳时间序列,通过差分将其转化为平稳序列,然后利用自回归和移动...
至于时间序列分析的特殊之处,文档指出许多最具有争议的问题都来自于时间序列分析。我们若想知道未来会发生什么,很大程度上要依赖于时间序列分析。同样,对于“自然实验”中的因果关系进行思考时,我们也会求助于...
时间序列分析-股票分析实现说明 HW1股票简单分析下载近半年的股价https://www.twse.com.tw/zh/page/trading/exchange/STOCK_ 第1天。平均价格/标准差、最高价格/最低价格和发生日期(筛选标准,如DF[DF['close']==...