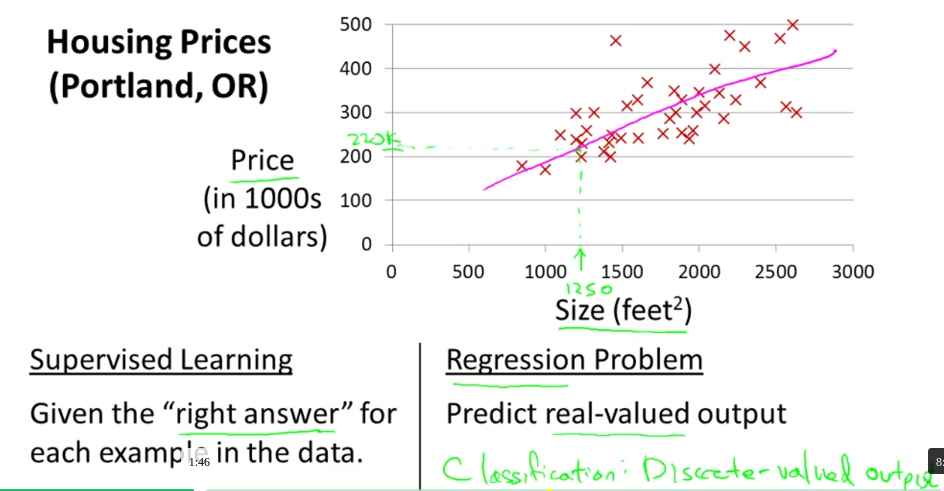
摘要: 给出一个房价预测的例子,x轴是房子的大小,y轴是房子的价格,图中标注了一些房子作为数据集,而这些点被称为标注数据(labeled data),利用这样的数据来预测的方法称为:监督学习。监督学习分为两类:分类与回归,此时,作为预测房价的这个例子是监督学习中的回归例子。
Linear Regression with one Variable(单变量线性回归)
Model and Cost Function(模型和损失函数)
给出一个房价预测的例子,x轴是房子的大小,y轴是房子的价格,图中标注了一些房子作为数据集,而这些点被称为标注数据(labeled data),利用这样的数据来预测的方法称为:监督学习。监督学习分为两类:分类与回归,此时,作为预测房价的这个例子是监督学习中的回归例子。
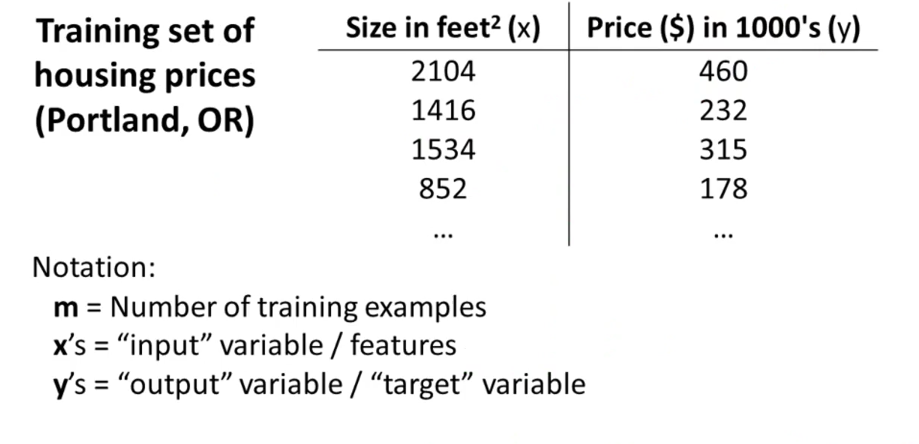
$m$代表是数据集的个数,$x's$是输入变量或者特征,$y's$是输出变量或者目标变量。
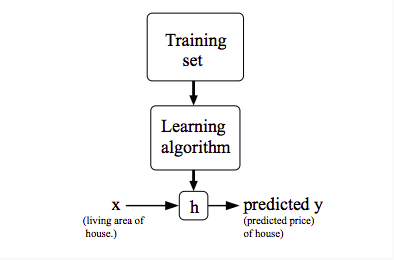
整个预测的过程可以归结为如下图:
通过训练数据,将数据输入到算法里面,我们能得到一个关于这个模型的一个假设$h$,然后利用这个假设$h$我们将其他输入变量输入到该假设中就会得到我们想要的预测结果$y$。那么对于单变量的线性回归我们用如下公式来表示:
线性模型其意思是模型是呈现线性变化的,为什么对于该房价的例子我们要采用单变量的,其原因是该模型的未知参数仅有一个$x$来决定。
对于假设函数其包含两个参数,$θ_0$和$θ_1$,那么如何来确定这两个参数来使得得出的假设函数直线更好的拟合数据集或者换句话说如何才能判断假设函数所产生的误差最小?
所以,给出如下定义:
第一个公式是最小化预测值与真实值差的平方的值,也叫作均方误差值,是衡量误差的一种方式。第二个公式是我们的假设函数。有时我们更喜欢写成如下形式:
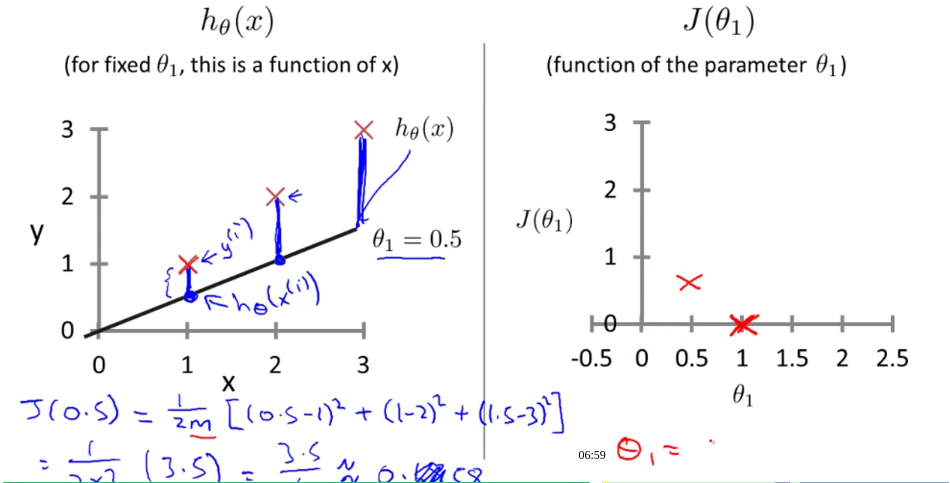
其中的$J(\theta_0,\theta_1)$叫做代价函数(cost function),我们的目的就是最小化代价函数,使得假设函数更加接近真实数据集。为了能更好的解释代价函数我们举个例子并画出能说明其含义的图来:
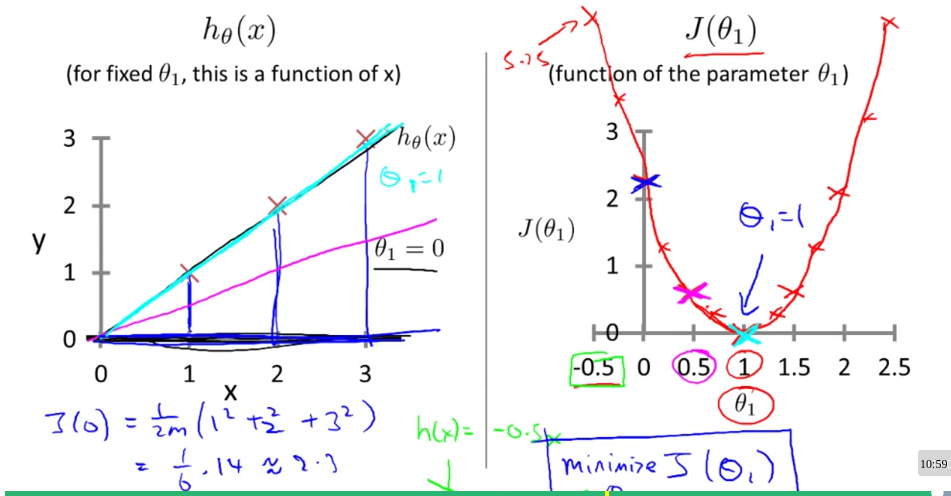
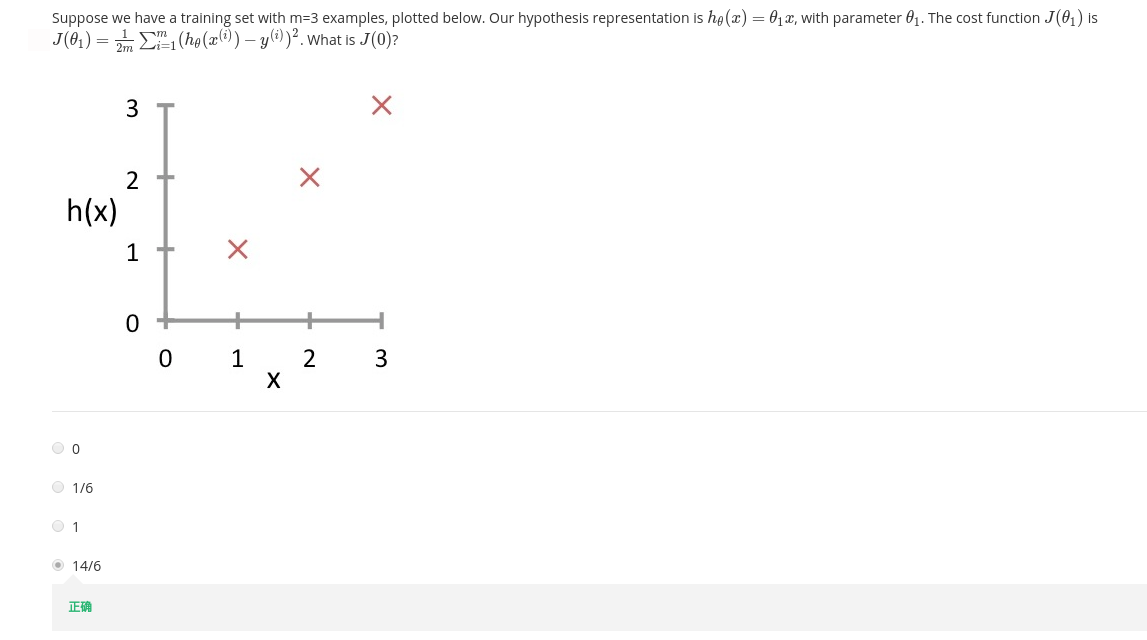
左边的图在坐标系中分别画了三个的点$(1,1)$,$(2,2)$,$(3,3)$,假设这就是我们的数据集,那么现在我们就要对这个数据集进行假设函数的猜测,当然,学过数学的人一眼就能看出在$\theta_0=0$,$\theta_1=1$时,也就是假设函数$h_\theta(x) = x$时是最吻合数据集的,但是假如该数据集不会这样简单,不能一眼看出它的拟合线来该怎么办呢?注意到,当假设函数越能拟合数据集时,它的代价函数就越接近$0$,所以这就是采用代价函数来选择参数$\theta_0$,$\theta_1$从而产生出更好的假设函数来拟合数据集的原因。
刚刚上面的例子图片采用的二维的图像,因为图片中只包含了两个参数,$\theta_1$和$J(\theta_1)$,如果是三个参数的图片则会映射到三维的图像上面上:







相关推荐
对于单变量线性回归,我们可以使用最小二乘法来求得解析解。最小二乘法的目标是最小化残差平方和,也就是所有数据点到直线的垂直距离的平方和。通过矩阵运算,可以将这个问题转换为求解系数向量 `θ`(包含 `w` 和 `...
综上所述,本文通过深入解析线性回归的定义、单变量和多变量线性回归的基本原理,以及梯度下降法的理论基础和Matlab实现步骤,展示了如何在Matlab环境下运用梯度下降算法来实现线性回归模型。此外,通过梯度下降法的...
相比线性回归,非线性回归模型更灵活,但可能更难解析和解释,且求解过程更为耗时。 在实际应用中,选择线性还是非线性回归取决于数据的性质和研究目标。如果数据分布呈现明显的线性趋势,线性回归是首选;当数据...
### Spark MLlib线性回归测试数据解析 #### 一、概览 在机器学习领域,尤其是针对大数据处理框架Apache Spark中的机器学习库MLlib(Machine Learning Library),线性回归是一种非常基础且重要的算法。它主要用于...
#### 多元线性回归原理 在数学上,多元线性回归模型可以表示为: \[ Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + ... + \beta_pX_p + \epsilon \] 其中, - \(Y\) 是因变量; - \(X_1, X_2, ..., X_p\) 是自变量; -...
在这个习题中,我们将探讨单变量线性回归和多变量线性回归,以及正规方程在解决线性回归问题中的应用。 首先,让我们了解一下单变量线性回归。单变量线性回归是最简单的线性模型,它通过建立一个直线方程来描述两个...
在这样的背景下,半参数线性回归模型应运而生,它结合了参数模型的解析优势和非参数模型的灵活性,成为处理这类问题的有效工具。本文将围绕MATLAB平台下半参数线性回归模型的核估计方法进行探讨,重点介绍最小二乘核...
内容概要:本文详细介绍了多元线性回归模型的概念、数学原理及其在实际中的应用。首先,阐述了多元线性回归作为线性回归扩展的重要性,并举例说明其用于多因素房价预测的应用。其次,从参数角度分析了公式构成,并...
在C++中实现线性回归可以帮助开发者更深入地理解算法原理,并将其应用于实际项目。本文将深入探讨线性回归(Linereg)算法及其在C++中的实现。 线性回归是一种基于最小二乘法的优化技术,它假设目标变量与输入特征...
在24.1.1节中,我们了解到线性回归模型假设因变量与自变量之间存在线性关系,这简化了问题并提供了易于解析的解决方案。24.1.2节则深入讨论了线性回归的损失函数(通常是平方误差损失)以及优化原理,如梯度下降(GD...
线性回归是一种广泛应用的统计分析方法,用于建立因变量与一个或多个自变量之间的线性关系模型。在给定的“线性回归.zip”压缩包中,包含了使用MATLAB实现线性回归算法的相关文件,特别是基于梯度下降的优化方法。...
### 多元线性回归模型代码解析 #### 一、多元线性回归简介 多元线性回归是一种统计学方法,用于研究一个连续型因变量(响应...通过对提供的代码进行深入分析,我们可以更好地理解多元线性回归的实现原理及其应用。
多元线性回归是一种统计分析方法,用于研究两个或多个自变量与一个因变量之间的关系。在C#编程环境中,实现多元线性回归通常涉及到数学计算库的使用,如Math.NET Numerics或者Accord.NET,这些库提供了数值计算和...
"线性回归分析练习题分析" 本文将对线性回归分析的实践题进行详细的解释和分析。 一、基础知识 线性回归分析是统计学中的...通过实践题,我们可以更好地理解线性回归分析的原理和应用,提高我们的统计学知识和技能。
多元线性回归是一种广泛应用的统计建模方法,用于预测一个连续变量(因变量)与多个独立变量(自变量)之间的关系。在这个情境中,我们利用梯度下降法来求解模型参数,这是一种优化算法,广泛用于机器学习和深度学习...
简单线性回归仅涉及一个自变量,而多元线性回归则可以考虑多个自变量。在Rust中实现线性回归,我们可以使用optimization库来求解最小二乘问题,或者利用线性代数库如nalgebra来直接解决线性方程组。 为了在Rust中...
通过这个实践,你可以掌握线性回归的基本原理和Octave的实现方法,了解如何处理不同维度的数据,以及如何评估模型的性能。此外,对于更复杂的任务,如特征选择、正则化等,也可以在此基础上进行进一步学习。线性回归...
一元线性回归模型是一种统计学方法,用于研究两个变量之间的线性关系,通常是自变量X和因变量Y。在这些习题中,我们看到了一些关键概念和术语的考察。 1. 变量关系的分类:变量之间的关系分为函数关系和相关关系。...
- **定义**:线性回归是一种通过拟合最佳线性关系来预测连续变量的方法。 - **应用场景**:在实际问题中,当我们希望根据已有的数据集来预测某个变量(例如生产能耗)时,可以使用线性回归方法。 2. **散点图绘制...
- 多元线性回归是一种统计方法,用于分析一个因变量(通常称为响应变量或被解释变量)与两个或多个自变量(也称为解释变量)之间的关系。 - 在本案例中,目标是通过分析生铁产量、原煤产量、电力产量、固定资本...