一、前言
concurrentHashMap与ConcurrentSkipListMap性能测试
在4线程1.6万数据的条件下,ConcurrentHashMap 存取速度是ConcurrentSkipListMap 的4倍左右。
但ConcurrentSkipListMap有几个ConcurrentHashMap 不能比拟的优点:
1、ConcurrentSkipListMap 的key是有序的。
2、ConcurrentSkipListMap 支持更高的并发。ConcurrentSkipListMap 的存取时间是log(N),和线程数几乎无关。也就是说在数据量一定的情况下,并发的线程越多,ConcurrentSkipListMap越能体现出他 的优势。
二、使用建议
在 非多线程的情况下,应当尽量使用TreeMap。此外对于并发性相对较低的并行程序可以使用 Collections.synchronizedSortedMap将TreeMap进行包装,也可以提供较好的效率。对于高并发程序,应当使用 ConcurrentSkipListMap,能够提供更高的并发度。
所以在多线程程序中,如果需要对Map的键值进行排序时,请尽量使用ConcurrentSkipListMap,可能得到更好的并发度。
注意,调用ConcurrentSkipListMap的size时,由于多个线程可以同时对映射表进行操作,所以映射表需要遍历整个链表才能返回元素个数,这个操作是个O(log(n))的操作。
二、什么是SkipList
Skip list(跳表)是一种可以代替平衡树的数据结构,默认是按照Key值升序的。Skip list让已排序的数据分布在多层链表中,以0-1随机数决定一个数据的向上攀升与否,通过“空间来换取时间”的一个算法,在每个节点中增加了向前的指 针,在插入、删除、查找时可以忽略一些不可能涉及到的结点,从而提高了效率。
从概率上保持数据结构的平衡比显示 的保持数据结构平衡要简单的多。对于大多数应用,用Skip list要比用树算法相对简单。由于Skip list比较简单,实现起来会比较容易,虽然和平衡树有着相同的时间复杂度(O(logn)),但是skip list的常数项会相对小很多。Skip list在空间上也比较节省。一个节点平均只需要1.333个指针(甚至更少)。

图1-1 Skip list结构图(以7,14,21,32,37,71,85序列为例)
Skip list的性质
(1) 由很多层结构组成,level是通过一定的概率随机产生的。
(2) 每一层都是一个有序的链表,默认是升序,也可以根据创建映射时所提供的Comparator进行排序,具体取决于使用的构造方法。
(3) 最底层(Level 1)的链表包含所有元素。
(4) 如果一个元素出现在Level i 的链表中,则它在Level i 之下的链表也都会出现。
(5) 每个节点包含两个指针,一个指向同一链表中的下一个元素,一个指向下面一层的元素。
三、什么是ConcurrentSkipListMap
ConcurrentSkipListMap提供了一种线程安全的并发访问的排序映射表。内部是SkipList(跳表)结构实现,在理论上能够在O(log(n))时间内完成查找、插入、删除操作。
注意,调用ConcurrentSkipListMap的size时,由于多个线程可以同时对映射表进行操作,所以映射表需要遍历整个链表才能返回元素个数,这个操作是个O(log(n))的操作。
ConcurrentSkipListMap存储结构

ConcurrentSkipListMap存储结构图
跳跃表(SkipList):(如上图所示)
1.多条链构成,是关键字升序排列的数据结构;
2.包含多个级别,一个head引用指向最高的级别,最低(底部)的级别,包含所有的key;
3.每一个级别都是其更低级别的子集,并且是有序的;
4.如果关键字 key在 级别level=i中出现,则,level<=i的链表中都会包含该关键字key;
------------------------
ConcurrentSkipListMap主要用到了Node和Index两种节点的存储方式,通过volatile关键字实现了并发的操作
- static final class Node<K,V> {
- final K key;
- volatile Object value;//value值
- volatile Node<K,V> next;//next引用
- ……
- }
- static class Index<K,V> {
- final Node<K,V> node;
- final Index<K,V> down;//downy引用
- volatile Index<K,V> right;//右边引用
- ……
- }
------------------------
ConcurrentSkipListMap的查找
通过SkipList的方式进行查找操作:(下图以“查找91”进行说明:)
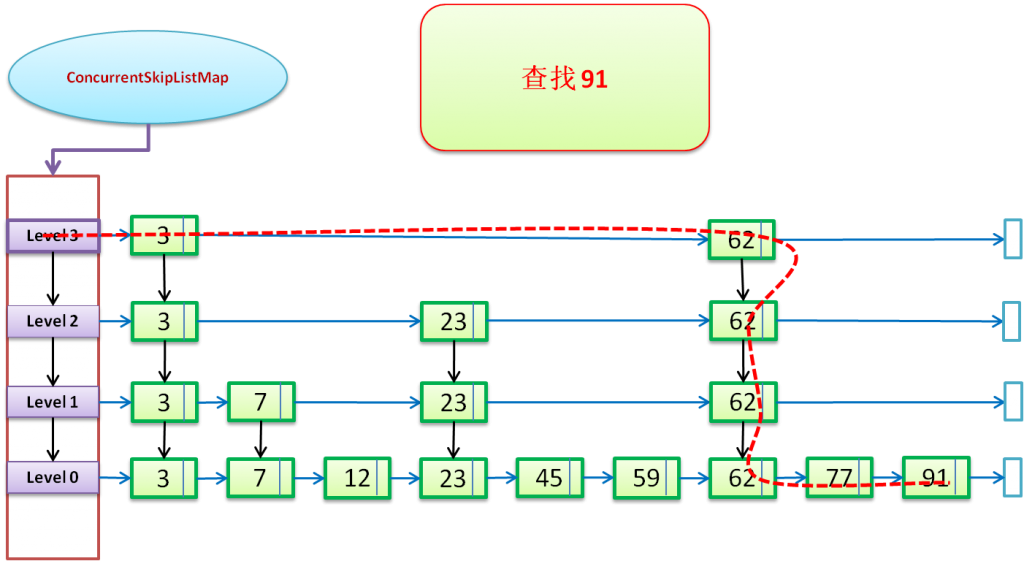
红色虚线,表示查找的路径,蓝色向右箭头表示right引用;黑色向下箭头表示down引用;
/get方法,通过doGet操作实现
- public V get(Object key) {
- return doGet(key);
- }
- //doGet的实现
- private V doGet(Object okey) {
- Comparable<? super K> key = comparable(okey);
- Node<K,V> bound = null;
- Index<K,V> q = head;//把头结点作为当前节点的前驱节点
- Index<K,V> r = q.right;//前驱节点的右节点作为当前节点
- Node<K,V> n;
- K k;
- int c;
- for (;;) {//遍历
- Index<K,V> d;
- // 依次遍历right节点
- if (r != null && (n = r.node) != bound && (k = n.key) != null) {
- if ((c = key.compareTo(k)) > 0) {//由于key都是升序排列的,所有当前关键字大于所要查找的key时继续向右遍历
- q = r;
- r = r.right;
- continue;
- } else if (c == 0) {
- //如果找到了相等的key节点,则返回该Node的value如果value为空可能是其他并发delete导致的,于是通过另一种
- //遍历findNode的方式再查找
- Object v = n.value;
- return (v != null)? (V)v : getUsingFindNode(key);
- } else
- bound = n;
- }
- //如果一个链表中right没能找到key对应的value,则调整到其down的引用处继续查找
- if ((d = q.down) != null) {
- q = d;
- r = d.right;
- } else
- break;
- }
- // 如果通过上面的遍历方式,还没能找到key对应的value,再通过Node.next的方式进行查找
- for (n = q.node.next; n != null; n = n.next) {
- if ((k = n.key) != null) {
- if ((c = key.compareTo(k)) == 0) {
- Object v = n.value;
- return (v != null)? (V)v : getUsingFindNode(key);
- } else if (c < 0)
- break;
- }
- }
- return null;
- }
------------------------------------------------
ConcurrentSkipListMap的删除
通过SkipList的方式进行删除操作:(下图以“删除23”进行说明:)
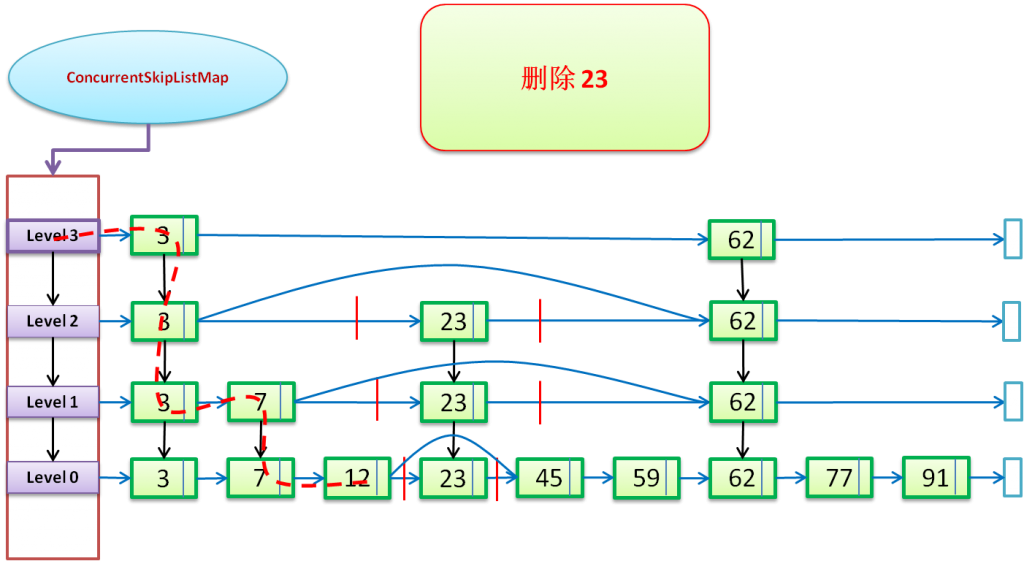
红色虚线,表示查找的路径,蓝色向右箭头表示right引用;黑色向下箭头表示down引用;
- //remove操作,通过doRemove实现,把所有level中出现关键字key的地方都delete掉
- public V remove(Object key) {
- return doRemove(key, null);
- }
- final V doRemove(Object okey, Object value) {
- Comparable<? super K> key = comparable(okey);
- for (;;) {
- Node<K,V> b = findPredecessor(key);//得到key的前驱(就是比key小的最大节点)
- Node<K,V> n = b.next;//前驱节点的next引用
- for (;;) {//遍历
- if (n == null)//如果next引用为空,直接返回
- return null;
- Node<K,V> f = n.next;
- if (n != b.next) // 如果两次获得的b.next不是相同的Node,就跳转到第一层循环重新获得b和n
- break;
- Object v = n.value;
- if (v == null) { // 当n被其他线程delete的时候,其value==null,此时做辅助处理,并重新获取b和n
- n.helpDelete(b, f);
- break;
- }
- if (v == n || b.value == null) // 当其前驱被delet的时候直接跳出,重新获取b和n
- break;
- int c = key.compareTo(n.key);
- if (c < 0)
- return null;
- if (c > 0) {//当key较大时就继续遍历
- b = n;
- n = f;
- continue;
- }
- if (value != null && !value.equals(v))
- return null;
- if (!n.casValue(v, null))
- break;
- if (!n.appendMarker(f) || !b.casNext(n, f))//casNext方法就是通过比较和设置b(前驱)的next节点的方式来实现删除操作
- findNode(key); // 通过尝试findNode的方式继续find
- else {
- findPredecessor(key); // Clean index
- if (head.right == null) //如果head的right引用为空,则表示不存在该level
- tryReduceLevel();
- }
- return (V)v;
- }
- }
- }
-------------------------------------
ConcurrentSkipListMap的插入
通过SkipList的方式进行插入操作:(下图以“添加55”的两种情况,进行说明:)
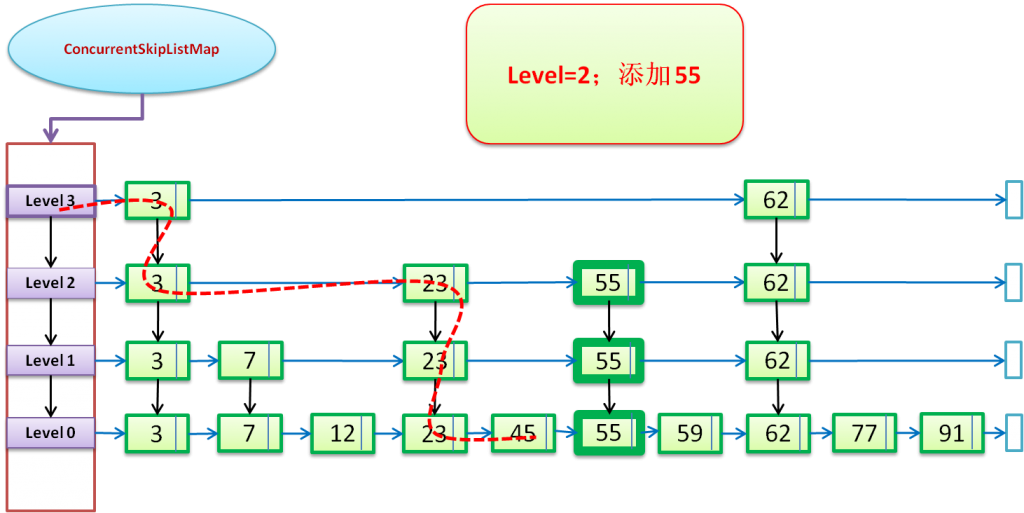
在level=2(该level存在)的情况下添加55的图示:只需在level<=2的合适位置插入55即可
--------

在level=4(该level不存在,图示level4是新建的)的情况下添加55的情况:首先新建level4,然后在level<=4的合适位置插入55
-----------
- //put操作,通过doPut实现
- public V put(K key, V value) {
- if (value == null)
- throw new NullPointerException();
- return doPut(key, value, false);
- }
- private V doPut(K kkey, V value, boolean onlyIfAbsent) {
- Comparable<? super K> key = comparable(kkey);
- for (;;) {
- Node<K,V> b = findPredecessor(key);//前驱
- Node<K,V> n = b.next;
- //定位的过程就是和get操作相似
- for (;;) {
- if (n != null) {
- Node<K,V> f = n.next;
- if (n != b.next) // 前后值不一致的情况下,跳转到第一层循环重新获得b和n
- break;;
- Object v = n.value;
- if (v == null) { // n被delete的情况下
- n.helpDelete(b, f);
- break;
- }
- if (v == n || b.value == null) // b 被delete的情况,重新获取b和n
- break;
- int c = key.compareTo(n.key);
- if (c > 0) {
- b = n;
- n = f;
- continue;
- }
- if (c == 0) {
- if (onlyIfAbsent || n.casValue(v, value))
- return (V)v;
- else
- break; // restart if lost race to replace value
- }
- // else c < 0; fall through
- }
- Node<K,V> z = new Node<K,V>(kkey, value, n);
- if (!b.casNext(n, z))
- break; // restart if lost race to append to b
- int level = randomLevel();//得到一个随机的level作为该key-value插入的最高level
- if (level > 0)
- insertIndex(z, level);//进行插入操作
- return null;
- }
- }
- }
- /**
- * 获得一个随机的level值
- */
- private int randomLevel() {
- int x = randomSeed;
- x ^= x << 13;
- x ^= x >>> 17;
- randomSeed = x ^= x << 5;
- if ((x & 0x8001) != 0) // test highest and lowest bits
- return 0;
- int level = 1;
- while (((x >>>= 1) & 1) != 0) ++level;
- return level;
- }
- //执行插入操作:如上图所示,有两种可能的情况:
- //1.当level存在时,对level<=n都执行insert操作
- //2.当level不存在(大于目前的最大level)时,首先添加新的level,然后在执行操作1
- private void insertIndex(Node<K,V> z, int level) {
- HeadIndex<K,V> h = head;
- int max = h.level;
- if (level <= max) {//情况1
- Index<K,V> idx = null;
- for (int i = 1; i <= level; ++i)//首先得到一个包含1~level个级别的down关系的链表,最后的inx为最高level
- idx = new Index<K,V>(z, idx, null);
- addIndex(idx, h, level);//把最高level的idx传给addIndex方法
- } else { // 情况2 增加一个新的级别
- level = max + 1;
- Index<K,V>[] idxs = (Index<K,V>[])new Index[level+1];
- Index<K,V> idx = null;
- for (int i = 1; i <= level; ++i)//该步骤和情况1类似
- idxs[i] = idx = new Index<K,V>(z, idx, null);
- HeadIndex<K,V> oldh;
- int k;
- for (;;) {
- oldh = head;
- int oldLevel = oldh.level;
- if (level <= oldLevel) { // lost race to add level
- k = level;
- break;
- }
- HeadIndex<K,V> newh = oldh;
- Node<K,V> oldbase = oldh.node;
- for (int j = oldLevel+1; j <= level; ++j)
- newh = new HeadIndex<K,V>(oldbase, newh, idxs[j], j);//创建新的
- if (casHead(oldh, newh)) {
- k = oldLevel;
- break;
- }
- }
- addIndex(idxs[k], oldh, k);
- }
- }
- /**
- *在1~indexlevel层中插入数据
- */
- private void addIndex(Index<K,V> idx, HeadIndex<K,V> h, int indexLevel) {
- // insertionLevel 代表要插入的level,该值会在indexLevel~1间遍历一遍
- int insertionLevel = indexLevel;
- Comparable<? super K> key = comparable(idx.node.key);
- if (key == null) throw new NullPointerException();
- // 和get操作类似,不同的就是查找的同时在各个level上加入了对应的key
- for (;;) {
- int j = h.level;
- Index<K,V> q = h;
- Index<K,V> r = q.right;
- Index<K,V> t = idx;
- for (;;) {
- if (r != null) {
- Node<K,V> n = r.node;
- // compare before deletion check avoids needing recheck
- int c = key.compareTo(n.key);
- if (n.value == null) {
- if (!q.unlink(r))
- break;
- r = q.right;
- continue;
- }
- if (c > 0) {
- q = r;
- r = r.right;
- continue;
- }
- }
- if (j == insertionLevel) {//在该层level中执行插入操作
- // Don't insert index if node already deleted
- if (t.indexesDeletedNode()) {
- findNode(key); // cleans up
- return;
- }
- if (!q.link(r, t))//执行link操作,其实就是inset的实现部分
- break; // restart
- if (--insertionLevel == 0) {
- // need final deletion check before return
- if (t.indexesDeletedNode())
- findNode(key);
- return;
- }
- }
- if (--j >= insertionLevel && j < indexLevel)//key移动到下一层level
- t = t.down;
- q = q.down;
- r = q.right;
- }
- }
- }
参考:
集合框架 Map篇(5)----ConcurrentSkipListMap http://hi.baidu.com/yao1111yao/item/0f3008163c4b82c938cb306d
Java里多个Map的性能比较(TreeMap、HashMap、ConcurrentSkipListMap) http://blog.hongtium.com/java-map-skiplist/
跳表SkipList的原理和实现 http://imtinx.iteye.com/blog/1291165







相关推荐
通过深入理解`ConcurrentSkipListMap`的实现,我们可以更好地应用它到并发编程中,以提升数据结构的性能和可扩展性。同时,这也为我们提供了一种思考并发数据结构设计的视角,帮助我们在解决实际问题时选择最适合的...
│ 高并发编程第一阶段27讲、wait和sleep的本质区别是什么,深入分析(面试常见问题).mp4 │ 高并发编程第一阶段28讲、线程生产者消费者的综合实战结合Java8语法.mp4 │ 高并发编程第一阶段29讲、如何实现一个...
│ 高并发编程第一阶段27讲、wait和sleep的本质区别是什么,深入分析(面试常见问题).mp4 │ 高并发编程第一阶段28讲、线程生产者消费者的综合实战结合Java8语法.mp4 │ 高并发编程第一阶段29讲、如何实现一个...
通过以上内容的介绍,读者应能更深入地理解Java集合框架中的Set接口及其各种实现的内部原理,并掌握如何在Java编程中使用这些集合来解决实际问题。同时,还应该对并发集合类有所了解,以及如何在多线程环境下安全地...
Collections API 提供了一些线程安全的集合实现,如`ConcurrentHashMap`, `CopyOnWriteArrayList`, 和 `ConcurrentSkipListMap`。这些类在多线程环境中能保证并发访问的安全,但要注意它们的设计目标和性能特性,...
JAVA后端架构师是指具有深入理解操作系统、网络、并发等技术底层知识的高级技术专家。他们能够熟练应对常见的并发编程问题,掌握至少一个常见中间件的源码,能够运用设计模式、OOA/D进行软件设计,并在微服务层面...
描述"A TreeMap for you to examine and analyze"提示我们,这个压缩包可能包含有关`TreeMap`的详细资料,供学习者深入研究和分析其内部工作原理、操作以及性能特点。 **`TreeMap`详解** `TreeMap`是Java中用于...
Java后端体系高级面试题是针对Java开发人员的深度技术面试准备材料,涵盖了广泛的Java...这些知识点是Java后端开发人员在面试过程中可能会遇到的,深入了解并掌握这些内容,将有助于提升个人的技术水平和面试竞争力。
《Java并发编程实践》这本书是Java开发者深入理解并发编程的重要参考资料。并发编程是现代多核处理器环境下不可或缺的技能,它涉及到如何在多个线程或进程之间有效地分配计算资源,以提高程序性能。Java语言提供了...
本项目"java_collection_source_code_analyze"专注于对Java集合框架的源代码进行深入分析,帮助开发者理解其内部机制,从而更好地利用这些工具。下面我们将详细探讨Java集合框架中的主要类、接口以及它们的实现和...
"最小松弛优先"是一种任务调度算法,...通过深入分析这些文件,我们可以更好地理解和学习如何在Java中实现和应用“最小松弛优先”算法。这将是一个有价值的资源,特别是对于那些对任务调度和优化感兴趣的Java开发者。
在计算机科学中,排序是数据处理的一个重要环节,尤其是在大数据处理和数据分析中。多线程技术则能够有效地利用现代多核处理器的计算能力,提高程序的执行效率。本主题主要探讨了三种经典的排序算法——希尔排序、...
理解并发容器如CopyOnWriteArrayList和ConcurrentSkipListMap的用途。 4. **内存管理**:理解Java的垃圾回收机制,包括引用类型(强引用、软引用、弱引用、虚引用),以及GC的基本原理和几种常见的垃圾收集器。 5....
本节将深入探讨Java中与树相关的关键概念和实现。 首先,我们来看一下Java API中提供的树相关类。`java.util.TreeSet`和`java.util.TreeMap`是两个基于红黑树实现的集合类,它们提供了有序的存储和高效的操作。`...