- 浏览: 373373 次
- 性别:

- 来自: 苏州
-

文章分类
- 全部博客 (335)
- C++ (190)
- 设计模式 (43)
- 数据库技术 (5)
- 网络编程 (11)
- 自动化测试 (6)
- Linux (13)
- OpenSSL (10)
- MS Crypt API (5)
- SCM (2)
- English (4)
- Android (10)
- EMV规范 (1)
- Saturn Platform (0)
- C (10)
- SQL (2)
- ASP.NET (3)
- 英语口语学习 (3)
- 调试工具 (21)
- 编译技术 (5)
- UML (1)
- 项目管理 (5)
- 敏捷开发 (2)
- Http Server (6)
- 代码审查、代码分析 (5)
- 面试基础 (10)
- 重点知识 (16)
- STL (6)
- Efficient C++资料 (8)
- 数据结构和算法 (7)
- 读书笔记 (0)
- 开源项目 (4)
- 多线程 (2)
- Console App (6)
- 个人开源项目 (4)
- IBM DevelopWorks (4)
- Java (16)
- 内存泄漏相关调试和检测 (13)
- 软件测试相关技术 (2)
- C# (11)
- Apple Related (1)
- 软件测试和管理 (2)
- EMV (1)
- Python (1)
- Node.js (6)
- JavaScript (5)
- VUE (1)
- Frontend (1)
- Backend (4)
- RESTful API (3)
- Firebase (3)
最新评论
-
u013189503:
来个密码吧
[C++][Logging] 项目中写日志模块的实现 -
wyf_vc:
来个密码啊!!
[C++][Logging] 项目中写日志模块的实现
参考
http://www.cnblogs.com/Jezze/archive/2011/12/23/2299884.html
http://blog.csdn.net/qyee16/article/details/6664377
https://mitpress.mit.edu/sicp/full-text/sicp/book/node41.html#fig:huffman
http://www.cnblogs.com/mcgrady/p/3329825.html
1、概述
huffman编码是一种可变长编码( VLC:variable length coding))方式,于1952年由huffman提出。依据字符在需要编码文件中出现的概率提供对字符的唯一编码,并且保证了可变编码的平均编码最短,被称为最优二叉树,有时又称为最佳编码。
2、原理
在了解huffman树为最优二叉树时,先要明确下面几个概念:
路径长度:树中一个节点到另一个节点之间分支构成这两个节点之间的路径,路径上的分支数目为其路径长度。
树的路径长度:树根到每一个节点的路径长度之和 为 “l”。
节点的带权路径长度:节点到树根之间的路径长度与节点上权的乘积。
树的带权路径长度:所有节点的带权路径长度之和,记作
n
WPL = ∑wk * lk 。
k=1
n个节点,权值为{ w1, w2, - - -,wn },把此n个节点为叶子节点,构造一个带n个节点叶子节点的二叉树,每个叶子节点的带权路径长度为wi。
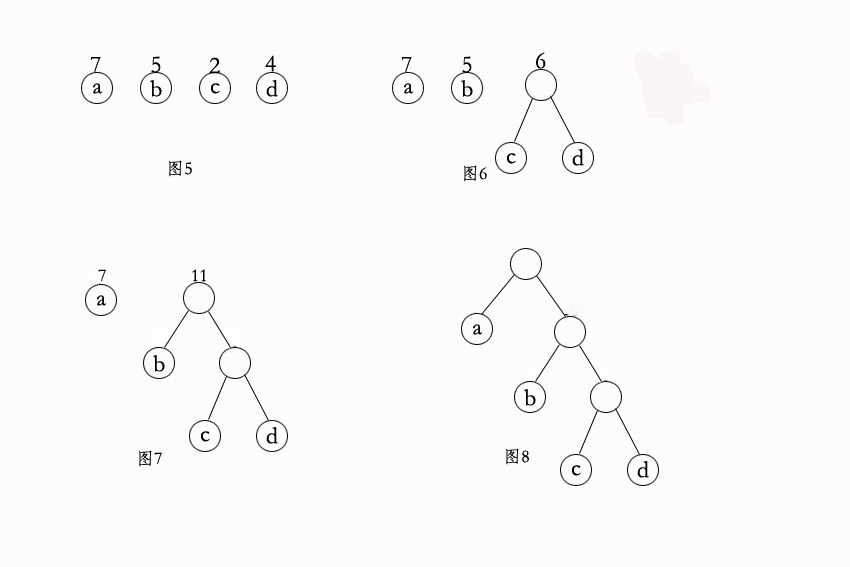
取节点a,b,c,d 其w[] = {2, 5, 7, 4},a=7 构造如下三棵树为例:

图1:wpl = 7*2 +5*2 + 2*2 + 4*2 = 36
图2:wpl = 7*3 + 5*3 + 2*1 + 4*2 = 46
图3:wpl = 7*1 + 5*2 + 2*3 + 4*3 = 35
可以证明(图3)其带权路径长度最短,就是huffman树。依次为两节点的连接线编码,左孩子为0,右孩子为1。那么图3就变成了(图33):

编码如下:a(0)、b(10)、c(110)、d(111)
不知道是否有人会问为什么a、b、c、d都是树的叶子节点,而不存在某个是父节点呢?试想,如果a是c、d的父节点,假设a的编码为0,其左右孩子是b、c,那么b,c的编码分别是00,和01,那么当出现诸如010001的压缩串时,可分别解释为caac,cbc,因为在出现a时,如果后面的编码为0,则不确定是解释为aa还是b了,出现歧义就出问题,所以字符只能出现在叶子节点。
在上面我们必须保证须编码的字符必须出现叶子节点,那我们怎么保证(图33)就是最短带权路径呢?我们下面一步步走下去构造huffman树,我们还假设a、b、c、d的带权为7、5、2,4。
3、构造huffman树过程
构造huffman树的哈夫曼算法如下:
(1)n节点的权值{w1、w2、·····,wn}构成n棵二叉树集合F={T1,T2,···,Tn},每棵二叉树Ti只有一个带权为Wi的根节点,左右孩子均空。
(2)在F中选取两棵根节点权值最小的作为树的左右孩子构造一棵新的二叉树,且置根节点的权值为左右孩子权值之和,在F中删除这两棵树,新二叉树之于F中
(3)重复(2),直到F中只有一棵树为止,这棵树就是huffman树。
上面就是以abcd四个节点构造huffman树的过程。
4、huffman代码
5、代码流程
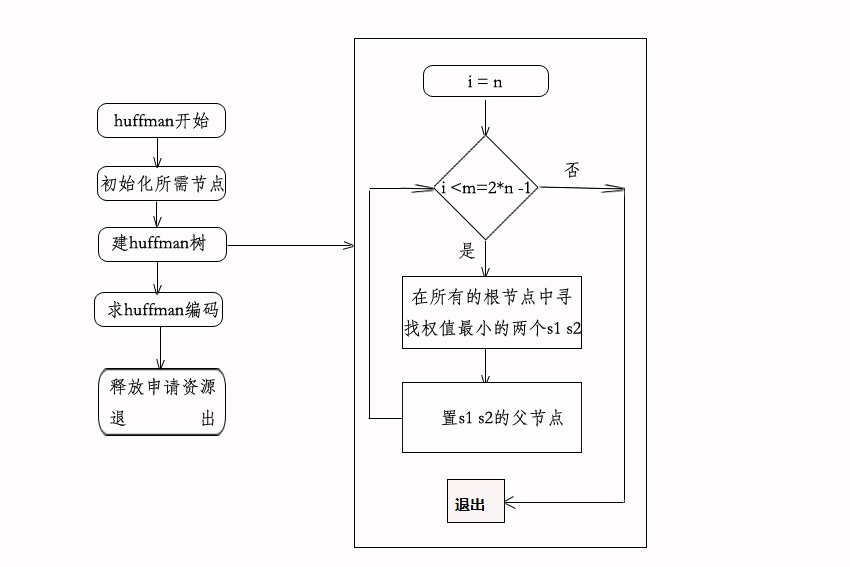
在一般的数据结构的书中,树的那章后面,著者一般都会介绍一下哈夫曼(HUFFMAN)树和哈夫曼编码。哈夫曼编码是哈夫曼树的一个应用。哈夫曼编码应用广泛,如JPEG中就应用了哈夫曼编码。 首先介绍什么是哈夫曼树。哈夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树。所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的 路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数)。树的带权路径长度记为WPL= (W1*L1+W2*L2+W3*L3+...+Wn*Ln),N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,...n)。可以证明哈夫曼树的WPL是最小的。
哈夫曼编码步骤:
一、对给定的n个权值{W1,W2,W3,...,Wi,...,Wn}构成n棵二叉树的初始集合F= {T1,T2,T3,...,Ti,...,Tn},其中每棵二叉树Ti中只有一个权值为Wi的根结点,它的左右子树均为空。(为方便在计算机上实现算 法,一般还要求以Ti的权值Wi的升序排列。)
二、在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树,新二叉树的根结点的权值为其左右子树的根结点的权值之和。
三、从F中删除这两棵树,并把这棵新的二叉树同样以升序排列加入到集合F中。
四、重复二和三两步,直到集合F中只有一棵二叉树为止。
简易的理解就是,假如我有A,B,C,D,E五个字符,出现的频率(即权值)分别为5,4,3,2,1,那么我们第一步先取两个最小权值作为左右子树构造一个新树,即取1,2构成新树,其结点为1+2=3,如图:
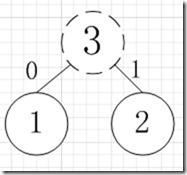
虚线为新生成的结点,第二步再把新生成的权值为3的结点放到剩下的集合中,所以集合变成{5,4,3,3},再根据第二步,取最小的两个权值构成新树,如图:
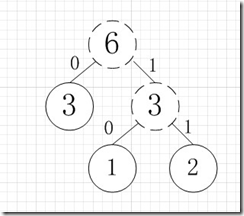
再依次建立哈夫曼树,如下图:
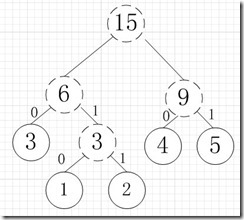
其中各个权值替换对应的字符即为下图:
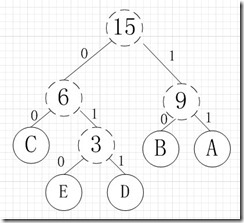
所以各字符对应的编码为:A->11,B->10,C->00,D->011,E->010
霍夫曼编码是一种无前缀编码。解码时不会混淆。其主要应用在数据压缩,加密解密等场合。
C语言代码实现:
http://www.cnblogs.com/Jezze/archive/2011/12/23/2299884.html
http://blog.csdn.net/qyee16/article/details/6664377
https://mitpress.mit.edu/sicp/full-text/sicp/book/node41.html#fig:huffman
http://www.cnblogs.com/mcgrady/p/3329825.html
1、概述
huffman编码是一种可变长编码( VLC:variable length coding))方式,于1952年由huffman提出。依据字符在需要编码文件中出现的概率提供对字符的唯一编码,并且保证了可变编码的平均编码最短,被称为最优二叉树,有时又称为最佳编码。
2、原理
在了解huffman树为最优二叉树时,先要明确下面几个概念:
路径长度:树中一个节点到另一个节点之间分支构成这两个节点之间的路径,路径上的分支数目为其路径长度。
树的路径长度:树根到每一个节点的路径长度之和 为 “l”。
节点的带权路径长度:节点到树根之间的路径长度与节点上权的乘积。
树的带权路径长度:所有节点的带权路径长度之和,记作
n
WPL = ∑wk * lk 。
k=1
n个节点,权值为{ w1, w2, - - -,wn },把此n个节点为叶子节点,构造一个带n个节点叶子节点的二叉树,每个叶子节点的带权路径长度为wi。
取节点a,b,c,d 其w[] = {2, 5, 7, 4},a=7 构造如下三棵树为例:

图1:wpl = 7*2 +5*2 + 2*2 + 4*2 = 36
图2:wpl = 7*3 + 5*3 + 2*1 + 4*2 = 46
图3:wpl = 7*1 + 5*2 + 2*3 + 4*3 = 35
可以证明(图3)其带权路径长度最短,就是huffman树。依次为两节点的连接线编码,左孩子为0,右孩子为1。那么图3就变成了(图33):

编码如下:a(0)、b(10)、c(110)、d(111)
不知道是否有人会问为什么a、b、c、d都是树的叶子节点,而不存在某个是父节点呢?试想,如果a是c、d的父节点,假设a的编码为0,其左右孩子是b、c,那么b,c的编码分别是00,和01,那么当出现诸如010001的压缩串时,可分别解释为caac,cbc,因为在出现a时,如果后面的编码为0,则不确定是解释为aa还是b了,出现歧义就出问题,所以字符只能出现在叶子节点。
在上面我们必须保证须编码的字符必须出现叶子节点,那我们怎么保证(图33)就是最短带权路径呢?我们下面一步步走下去构造huffman树,我们还假设a、b、c、d的带权为7、5、2,4。
3、构造huffman树过程

构造huffman树的哈夫曼算法如下:
(1)n节点的权值{w1、w2、·····,wn}构成n棵二叉树集合F={T1,T2,···,Tn},每棵二叉树Ti只有一个带权为Wi的根节点,左右孩子均空。
(2)在F中选取两棵根节点权值最小的作为树的左右孩子构造一棵新的二叉树,且置根节点的权值为左右孩子权值之和,在F中删除这两棵树,新二叉树之于F中
(3)重复(2),直到F中只有一棵树为止,这棵树就是huffman树。
上面就是以abcd四个节点构造huffman树的过程。
4、huffman代码
// Huffman coding.cpp : 定义控制台应用程序的入口点。
//Copyright@Qyee, 2011-7-30
#include "stdafx.h"
#include <iostream>
#include <Windows.h>
using namespace std;
//huffman tree节点定义
typedef struct
{
int weight; //保存权值
int parent, lchild, rchild; //保存左右孩子的节点值
}HuffmanNode, *HuffmanTree;
typedef char **HuffmanCode;
void HuffmanCoding(HuffmanTree &HT, int *w, int n); //Huffman编码函数
void select(HuffmanTree HT,int n, int &s1, int &s2);//选择书中节点值较小的两个节点
void Error(char* message); //显示错误信息
int w[] = {2, 5, 7, 4}; //各节点权值
int main(int argc, char* argv[])
{
HuffmanTree HT;
HuffmanCoding(HT, w, 6);
getchar(); //在win7系统,防止直接跳出,接收字符才执行return语句
return 0;
}
void HuffmanCoding(HuffmanTree &HT, int *w, int n)
{
if (n <= 1)
Error("code is small");
int m = 2 * n - 1; //n nodes create huffman tree need 2n-1 nodes
HT = (HuffmanNode*)malloc((m + 1) * sizeof(HuffmanNode));//Huffman tree的所有节点
int s1, s2; //record the two mini weights nodes
memset(HT, 0, (m + 1)* sizeof(HuffmanNode)); //对所有节点初始化为-0
//set the n nodes
for (int i = 1; i <= n; i++)
{
HT[i].weight = *w++; //初始化各节点权值
}
//创建Huffman tree
for(int i = n + 1; i <= m; ++i)
{
//选择剩余节点中权值较小的s1和s2
select(HT, i - 1, s1, s2);
HT[s1].parent = i;
HT[s2].parent = i;
HT[i].lchild = s1;
HT[i].rchild = s2;
HT[i].weight = HT[s1].weight + HT[s2].weight;
}
HuffmanCode HC;
int start, c, f;
HC = (HuffmanCode)malloc((n + 1) * sizeof(char*));
char* cd = (char*)malloc(n * sizeof(char));
cd[n - 1] = '\0';
for(int i = 1; i <= n; ++i)
{
start = n - 1;
for(c = i, f = HT[i].parent; f != 0; c = f, f = HT[f].parent)
if (HT[f].lchild == c)
cd[--start] = '0';
else
cd[--start] = '1';
HC[i] = (char*)malloc((n - start) * sizeof(char));
strcpy(HC[i], &cd[start]);
}
for (int i = 1; i <= n; i++)
{
cout<<HC[i]<<endl;
}
free(cd);
free(HC);
free(HT);
}
void Error(char* message)
{
fprintf(stderr, "Error: %s(5s will exit)", message);
cout<<"\n";
Sleep(5000);
exit(1);
}
void select(HuffmanTree HT, int n, int &s1, int &s2)
{
s1 = 1;
s2 = 1;
int min = 99999;
int i;
//选择未被使用的第一个节点,
for (i = 1; i <= n; ++i)
{
if (HT[i].parent == 0)
{
min = HT[i].weight;
break;
}
}
//find the mini s1
for (int p = 1; p <= n; ++p)
{
if(0 == HT[p].parent && min >= HT[p].weight)
{
s1 = p;
min = HT[p].weight;
}
}
//find the s2
min = 99999;
for (int q = 1; q <= n; ++q)
{
if(0 == HT[q].parent && min >= HT[q].weight )
{
if( q == s1)
continue;
s2 = q;
min = HT[q].weight;
}
}
}
5、代码流程

在一般的数据结构的书中,树的那章后面,著者一般都会介绍一下哈夫曼(HUFFMAN)树和哈夫曼编码。哈夫曼编码是哈夫曼树的一个应用。哈夫曼编码应用广泛,如JPEG中就应用了哈夫曼编码。 首先介绍什么是哈夫曼树。哈夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树。所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的 路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数)。树的带权路径长度记为WPL= (W1*L1+W2*L2+W3*L3+...+Wn*Ln),N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,...n)。可以证明哈夫曼树的WPL是最小的。
哈夫曼编码步骤:
一、对给定的n个权值{W1,W2,W3,...,Wi,...,Wn}构成n棵二叉树的初始集合F= {T1,T2,T3,...,Ti,...,Tn},其中每棵二叉树Ti中只有一个权值为Wi的根结点,它的左右子树均为空。(为方便在计算机上实现算 法,一般还要求以Ti的权值Wi的升序排列。)
二、在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树,新二叉树的根结点的权值为其左右子树的根结点的权值之和。
三、从F中删除这两棵树,并把这棵新的二叉树同样以升序排列加入到集合F中。
四、重复二和三两步,直到集合F中只有一棵二叉树为止。
简易的理解就是,假如我有A,B,C,D,E五个字符,出现的频率(即权值)分别为5,4,3,2,1,那么我们第一步先取两个最小权值作为左右子树构造一个新树,即取1,2构成新树,其结点为1+2=3,如图:

虚线为新生成的结点,第二步再把新生成的权值为3的结点放到剩下的集合中,所以集合变成{5,4,3,3},再根据第二步,取最小的两个权值构成新树,如图:

再依次建立哈夫曼树,如下图:

其中各个权值替换对应的字符即为下图:

所以各字符对应的编码为:A->11,B->10,C->00,D->011,E->010
霍夫曼编码是一种无前缀编码。解码时不会混淆。其主要应用在数据压缩,加密解密等场合。
C语言代码实现:
/*-------------------------------------------------------------------------
* Name: 哈夫曼编码源代码。
* Date: 2011.04.16
* Author: Jeffrey Hill+Jezze(解码部分)
* 在 Win-TC 下测试通过
* 实现过程:着先通过 HuffmanTree() 函数构造哈夫曼树,然后在主函数 main()中
* 自底向上开始(也就是从数组序号为零的结点开始)向上层层判断,若在
* 父结点左侧,则置码为 0,若在右侧,则置码为 1。最后输出生成的编码。
*------------------------------------------------------------------------*/
#include <stdio.h>
#include<stdlib.h>
#define MAXBIT 100
#define MAXVALUE 10000
#define MAXLEAF 30
#define MAXNODE MAXLEAF*2 -1
typedef struct
{
int bit[MAXBIT];
int start;
} HCodeType; /* 编码结构体 */
typedef struct
{
int weight;
int parent;
int lchild;
int rchild;
int value;
} HNodeType; /* 结点结构体 */
/* 构造一颗哈夫曼树 */
void HuffmanTree (HNodeType HuffNode[MAXNODE], int n)
{
/* i、j: 循环变量,m1、m2:构造哈夫曼树不同过程中两个最小权值结点的权值,
x1、x2:构造哈夫曼树不同过程中两个最小权值结点在数组中的序号。*/
int i, j, m1, m2, x1, x2;
/* 初始化存放哈夫曼树数组 HuffNode[] 中的结点 */
for (i=0; i<2*n-1; i++)
{
HuffNode[i].weight = 0;//权值
HuffNode[i].parent =-1;
HuffNode[i].lchild =-1;
HuffNode[i].rchild =-1;
HuffNode[i].value=i; //实际值,可根据情况替换为字母
} /* end for */
/* 输入 n 个叶子结点的权值 */
for (i=0; i<n; i++)
{
printf ("Please input weight of leaf node %d: \n", i);
scanf ("%d", &HuffNode[i].weight);
} /* end for */
/* 循环构造 Huffman 树 */
for (i=0; i<n-1; i++)
{
m1=m2=MAXVALUE; /* m1、m2中存放两个无父结点且结点权值最小的两个结点 */
x1=x2=0;
/* 找出所有结点中权值最小、无父结点的两个结点,并合并之为一颗二叉树 */
for (j=0; j<n+i; j++)
{
if (HuffNode[j].weight < m1 && HuffNode[j].parent==-1)
{
m2=m1;
x2=x1;
m1=HuffNode[j].weight;
x1=j;
}
else if (HuffNode[j].weight < m2 && HuffNode[j].parent==-1)
{
m2=HuffNode[j].weight;
x2=j;
}
} /* end for */
/* 设置找到的两个子结点 x1、x2 的父结点信息 */
HuffNode[x1].parent = n+i;
HuffNode[x2].parent = n+i;
HuffNode[n+i].weight = HuffNode[x1].weight + HuffNode[x2].weight;
HuffNode[n+i].lchild = x1;
HuffNode[n+i].rchild = x2;
printf ("x1.weight and x2.weight in round %d: %d, %d\n", i+1, HuffNode[x1].weight, HuffNode[x2].weight); /* 用于测试 */
printf ("\n");
} /* end for */
/* for(i=0;i<n+2;i++)
{
printf(" Parents:%d,lchild:%d,rchild:%d,value:%d,weight:%d\n",HuffNode[i].parent,HuffNode[i].lchild,HuffNode[i].rchild,HuffNode[i].value,HuffNode[i].weight);
}*///测试
} /* end HuffmanTree */
//解码
void decodeing(char string[],HNodeType Buf[],int Num)
{
int i,tmp=0,code[1024];
int m=2*Num-1;
char *nump;
char num[1024];
for(i=0;i<strlen(string);i++)
{
if(string[i]=='0')
num[i]=0;
else
num[i]=1;
}
i=0;
nump=&num[0];
while(nump<(&num[strlen(string)]))
{tmp=m-1;
while((Buf[tmp].lchild!=-1)&&(Buf[tmp].rchild!=-1))
{
if(*nump==0)
{
tmp=Buf[tmp].lchild ;
}
else tmp=Buf[tmp].rchild;
nump++;
}
printf("%d",Buf[tmp].value);
}
}
int main(void)
{
HNodeType HuffNode[MAXNODE]; /* 定义一个结点结构体数组 */
HCodeType HuffCode[MAXLEAF], cd; /* 定义一个编码结构体数组, 同时定义一个临时变量来存放求解编码时的信息 */
int i, j, c, p, n;
char pp[100];
printf ("Please input n:\n");
scanf ("%d", &n);
HuffmanTree (HuffNode, n);
for (i=0; i < n; i++)
{
cd.start = n-1;
c = i;
p = HuffNode[c].parent;
while (p != -1) /* 父结点存在 */
{
if (HuffNode[p].lchild == c)
cd.bit[cd.start] = 0;
else
cd.bit[cd.start] = 1;
cd.start--; /* 求编码的低一位 */
c=p;
p=HuffNode[c].parent; /* 设置下一循环条件 */
} /* end while */
/* 保存求出的每个叶结点的哈夫曼编码和编码的起始位 */
for (j=cd.start+1; j<n; j++)
{ HuffCode[i].bit[j] = cd.bit[j];}
HuffCode[i].start = cd.start;
} /* end for */
/* 输出已保存好的所有存在编码的哈夫曼编码 */
for (i=0; i<n; i++)
{
printf ("%d 's Huffman code is: ", i);
for (j=HuffCode[i].start+1; j < n; j++)
{
printf ("%d", HuffCode[i].bit[j]);
}
printf(" start:%d",HuffCode[i].start);
printf ("\n");
}
/* for(i=0;i<n;i++){
for(j=0;j<n;j++)
{
printf ("%d", HuffCode[i].bit[j]);
}
printf("\n");
}*/
printf("Decoding?Please Enter code:\n");
scanf("%s",&pp);
decodeing(pp,HuffNode,n);
getch();
return 0;
}
- 数据结构和算法系列16_哈夫曼树.zip (205.4 KB)
- 下载次数: 0
发表评论
-
FreeRTOS
2022-03-05 16:31 253Ref https://blog.csdn.net/weix ... -
串口通讯相关
2018-11-02 13:44 417https://bbs.csdn.net/wap/topics ... -
[转]C++验证IP是否可以PING通
2018-10-30 17:54 1346https://www.cnblogs.com/guoyz13 ... -
C++/MFC 換皮膚
2018-10-20 11:05 481https://blog.csdn.net/u01123991 ... -
WinCE 截屏 - C++ 代碼
2018-08-31 09:45 580// this function create a bmp ... -
Android NDK搭建環境
2017-11-27 13:25 593https://www.cnblogs.com/ut2016- ... -
8583协议相关
2017-10-17 13:38 5828583相关资料,整理中... -
Java高级应用之JNI
2017-06-19 09:00 609参考link http://www.cnblogs.com/l ... -
C++实现ping功能
2017-04-18 11:21 2176基础知识 ping的过程是向目的IP发送一个type=8的I ... -
OpenSSL 编译环境搭建
2017-03-27 15:01 9161 安裝VS2008到 c:\Program Files (x ... -
最优非对称加密填充(OAEP)
2017-03-25 14:53 1596OpenSSL命令---rsautl http://blog. ... -
[Platform Builder] 设置SVM OS build Env
2016-11-10 11:39 01 copy one OSDesign Project to ... -
[Windows] System Error Codes(GetLastError )0-----5999
2016-10-26 13:28 1886ERROR_SUCCESS 0 (0x0) T ... -
开源Windows驱动程序框架
2016-09-17 21:35 878转自 http://code.csdn.net/news/28 ... -
c/c++代码中执行cmd命令
2016-09-14 14:50 1926转自 http://blog.csdn.net/slixinx ... -
C#使用C++标准DLL实例(包含callback)
2016-09-11 19:44 1095C++编写标准Win32DLL如下 头文件 /***** ... -
C#调用C++的DLL搜集整理的所有数据类型转换方式
2016-09-09 16:07 974转自 http://www.cnblogs.com/zeroo ... -
WinCE CPU使用率计算 测试工具
2016-09-08 16:14 1006转自 http://blog.csdn.net/jan ... -
switch在C++与C#中的一些差异
2016-09-08 15:19 821参考链接 http://blog.csdn.net/weiwe ... -
C++ 鼠标模拟程序
2016-09-04 12:09 1623转自 http://blog.csdn.net/weixinh ...





相关推荐
运用哈夫曼算法构造哈夫曼树,并得到哈夫曼编码。 输入格式:10,5,21,18,8,13 二、实验目的 掌握哈夫曼算法。 三、实验内容及要求 1、构造哈夫曼树和哈夫曼编码的存储结构。 2、实现哈夫曼算法,实现哈夫曼树的存储...
哈夫曼树与哈夫曼编码是数据结构和算法领域中的重要概念,主要应用于数据压缩和效率优化。它们是基于贪心策略的高效算法,旨在最小化带权路径长度(WPL),从而达到最佳编码的效果。 哈夫曼树,又称为最优二叉树或...
### 哈夫曼树与哈夫曼编码详解 #### 一、哈夫曼树概述 **哈夫曼树**,又称最优二叉树,是一种带权路径长度最短的二叉树,其中的权值是指树中结点被赋予的数值。在哈夫曼树中,每个叶子结点代表一个字符或符号,...
### 哈夫曼树与哈夫曼编码详解 #### 一、哈夫曼树概述 **哈夫曼树(Huffman Tree)**是一种特殊类型的二叉树,它由美国计算机科学家大卫·哈夫曼(David A. Huffman)在1952年提出。哈夫曼树主要用于数据压缩,...
### 哈夫曼树与哈夫曼编码 #### 哈夫曼树的基本概念 哈夫曼树,又称作最优二叉树,是一种特殊的二叉树结构,在数据压缩领域有着重要的应用价值。它主要用于构建一种高效的数据压缩模型,通过减少数据传输或存储时...
总之,哈夫曼树与哈夫曼编码是数据压缩的基础,它们通过优化频率高的字符编码长度,提高了压缩效率。C++作为一门强大的编程语言,提供了丰富的库函数支持实现这些算法,使得在实际项目中应用哈夫曼编码成为可能。
《哈夫曼树与哈夫曼编码》 哈夫曼树(Huffman Tree),又称为最优二叉树,是一种特殊的二叉树结构,主要用于数据压缩和编码。它是由美国计算机科学家大卫·艾伦·哈夫曼(David A. Huffman)在1952年提出的,故以此...
《实验四 哈夫曼树与哈夫曼编码》 哈夫曼树(Huffman Tree),又称为最优二叉树,是一种特殊的二叉树,广泛应用于数据压缩领域,特别是在文本压缩中起到关键作用。它的构造基于哈夫曼编码(Huffman Coding),这是...
哈夫曼树(Huffman Tree)和哈夫曼编码(Huffman Coding)是数据压缩领域中的基础算法,它们主要用于无损数据...通过理解和实现哈夫曼树与哈夫曼编码,我们可以深入理解数据压缩的原理,并能设计出更高效的压缩算法。
【哈夫曼树与哈夫曼编码】 哈夫曼树是一种特殊的二叉树,由美国计算机科学家大卫·哈夫曼于1952年提出,主要用于数据压缩和编码。哈夫曼树是一种带权路径长度最短的二叉树,也被称作最优二叉树。在哈夫曼树中,频率...