- 浏览: 378748 次
- 性别:

- 来自: 苏州
-

文章分类
- 全部博客 (335)
- C++ (190)
- 设计模式 (43)
- 数据库技术 (5)
- 网络编程 (11)
- 自动化测试 (6)
- Linux (13)
- OpenSSL (10)
- MS Crypt API (5)
- SCM (2)
- English (4)
- Android (10)
- EMV规范 (1)
- Saturn Platform (0)
- C (10)
- SQL (2)
- ASP.NET (3)
- 英语口语学习 (3)
- 调试工具 (21)
- 编译技术 (5)
- UML (1)
- 项目管理 (5)
- 敏捷开发 (2)
- Http Server (6)
- 代码审查、代码分析 (5)
- 面试基础 (10)
- 重点知识 (16)
- STL (6)
- Efficient C++资料 (8)
- 数据结构和算法 (7)
- 读书笔记 (0)
- 开源项目 (4)
- 多线程 (2)
- Console App (6)
- 个人开源项目 (4)
- IBM DevelopWorks (4)
- Java (16)
- 内存泄漏相关调试和检测 (13)
- 软件测试相关技术 (2)
- C# (11)
- Apple Related (1)
- 软件测试和管理 (2)
- EMV (1)
- Python (1)
- Node.js (6)
- JavaScript (5)
- VUE (1)
- Frontend (1)
- Backend (4)
- RESTful API (3)
- Firebase (3)
最新评论
-
u013189503:
来个密码吧
[C++][Logging] 项目中写日志模块的实现 -
wyf_vc:
来个密码啊!!
[C++][Logging] 项目中写日志模块的实现
转自
http://blog.csdn.net/bjyfb/article/details/7519360
http://blog.csdn.net/bjyfb/article/details/7522000
二叉树遍历实例代码


二叉树并不是一种特殊的树,是一种独立的数据结构。下面是一些关于二叉树入门级的、纯理论的东东,高手请Alt+F4,千万别往下翻,会影响您的心情!
二叉树的分类
满二叉树:除最后一层无任何子节点外,每一层上的所有结点都有两个子结点。
完全二叉树:除了最下面一层,其他层结点都是饱满的,并且最下层上的结点都集中在该层最左边的若干位置上。(满二叉树也是完全二叉树)
非完全二叉树:既不是满二叉树,也非完全二叉树。
例:

二叉树的遍历
前序遍历(先根遍历):根左右。
后序遍历(后根遍历):左右根。
中序遍历(中根遍历):左跟右。
层次遍历:一层一层自左向右。
例:

图中前序遍历结果是:1,2,4,5,7,8,3,6;
图中中序遍历结果是:4,2,7,8,5,1,3,6;
图中后序遍历结果是:4,8,7,5,2,6,3,1;
图中层次遍历结果是:1,2,3,4,5,6,7,8;
树和二叉树的转换
将树的孩子结点转成二叉树的左子结点,树的兄弟结点转成二叉树的右子结点。
例:

二叉树的一些重要特性
1、在二叉树的第i层上最多有2^(n-1)个结点(i>=1);
例:以图1为例:任一图中第2层,最多只能有2个结点。验证正确!
2、深度为k的二叉树最多有2^k - 1个结点(K>=1);
例:以图1为例:图中所有二叉树深度为3,因此,该些二叉树最多有2^3 -1 = 7个结点,验证正确!
3、对任何一颗二叉树,如果其叶子结点数为n0,度为2的结点数为n2,则n0 = n2 + 1;
例:以图1为例:看最后一个非完全二叉树,图中所示,叶子结点n0 = 2;度为2的结点n2 = 1(结点2);则2 = 1 + 1。验证正确!
4、如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到⌊log2n⌋ + 1层,每层从左到右),则对任一结点i(1<=i<=n),(⌊⌋向下取整符号) 有:
如果i=1,则结点i无父节点,是二叉树的根;如果i>1,则父节点是⌊i/2⌋ ;
例:
以图1左侧的完全二叉树为例:若i = 3,则i > 1,⌊3/2⌋ = 1,3的根结点为1。验证 正确!
如果2i>n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
例:
以图1左侧的完全二叉树为例:若i = 3,因 n = 5,则2i>n,由此推出3为叶子结点。若i = 2,因 n = 5,则2i<n,由此推出2的左子结点为4。验证正确!
如果2i+1>n,则结点i无右子结点,否则,其右子结点是结点2i + 1。
例:
以图1左侧的完全二叉树为例:上一条否命题求出了左子树结点,而这条正好求出了右子树结点。结点i=2的右子树结点为5,验证正确!
查找二叉树(二叉排序树)
二叉排序树(Binary Sort Tree)又称二叉查找树(Binary Search Tree)。其定义为:二叉排序树或者是空树,或者是满足如下性质的二叉树:
①若它的左子树非空,则左子树上所有结点的值均小于根结点的值;
②若它的右子树非空,则右子树上所有结点的值均大于根结点的值;
③左、右子树本身又各是一棵二叉排序树。
例:
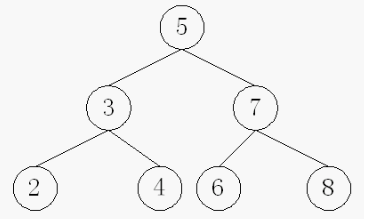
对排序二叉树的一些操作
查找:若根结点的关键字值等于查找的关键字,成功。
否则,若小于根结点的关键字值,递归查左子树。
若大于根结点的关键字值,递归查右子树。
若子树为空,查找不成功。
插入:分以下几种情况进行相应的处理:
①如果相同键值的结点已在查找二叉树中,则不再插入;
②如果查找二叉树为空树,则以新结点为查找二叉树;
③将要插入结点的键值与插入后的父结点的键值比较,就能确定新结点是父结点的左子结点,还是右子结点,并进行相应插入,新插入的结点一定是一个新添加的叶子结点。
删除:分以下几种情况进行相应的处理:
①若待删除的结点p是叶子结点,则直接删除该结点;
②若待删除的结点p只有一个子节点,则将这个子结点与待删除结点的父结点直接连接,然后删除节点p;
③若待删除的结点p有两个子结点,则在其左子树上,用中序遍历寻找关健值最大的结点s,用结点s的值代替结点p的值,然后删除节点s,结点s必属于上述①、②情况之一。
例:删除图1中的根结点5
首先,中序遍历结点5的左子树,获得最大的结点s=4,将p=5和s=4互换位置,发现要删除的p结点属于第①种情况,则直接删除p=5结点。
最优二叉树(哈夫曼树)
最优二叉树是带权路径长度最小的树。
基本术语
树的路径长度:是从树根到树中每一个结点的路径长度之和。在结点数目相同的二叉树中,完全二叉树的路径长度最短。
结点的权:根据应用的需要给树的结点赋的权值。
带权路径长度:结点到树根之间的路径长度与该结点上权的乘积,称为结点的带权路径长度。
树的带权路径长度(树的代价):树中所有叶结点的带权路径长度之和,称为树的代价。
构造哈夫曼树

哈弗曼编码
求出哈夫曼树后,以上图为例,只需人为规定左侧为0,右侧为1,那么结点23的编码是:00;结点11的编码是:010。哈夫曼编码是一种应用广泛且非常有效的数据压缩技术,该技术一般可将数据文件压缩掉20%-90%,其压缩效率取决于被压缩文件的特征。
线索二叉树
二叉树的遍历本质上是将一个复杂的非线性结构转换为线性结构,使每个结点都有了唯一前驱和后继(第一个结点无前驱,最后一个结点无后继)。对于二叉树的一个结点,查找其左右子女是方便的,其前驱后继只有在遍历中得到。为了容易找到前驱和后继,有两种方法。一是在结点结构中增加向前和向后的指针fwd和bkd,这种方法增加了存储开销,不可取;二是利用二叉树的空链指针。现将二叉树的结点结构重新定义如下:

对于标志域规定如下:
Lbit=0,Lchild是通常的指正;Lbit=1,Lchild是线索;
Rbit=0,Rchild是通常的指针;Rbit=1,Rchild是线索;
将二叉树转化为线索二叉树
第一步:将将二叉树的前序遍历、中序遍历、后序遍历的顺序写下来;
下图前序遍历顺序:A B D E H C F G I
中序遍历:D B H E A F C G I
后序遍历:D H E B F I G C A
第二步:参照遍历的顺序,找到各个结点对应的前驱和后驱,如下图:
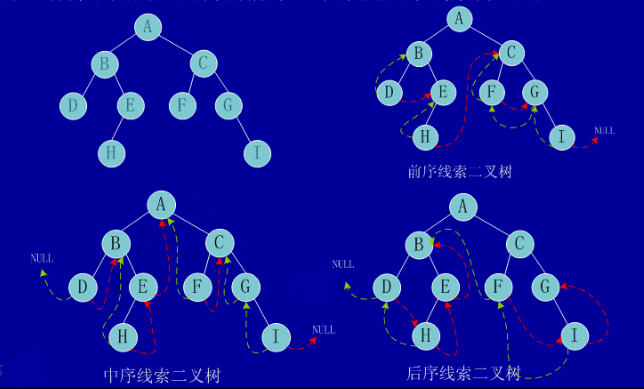
绿色线表示前驱;红色线表示后驱。
上面提到线索二叉树的使用就是为了方便的找到前驱和后驱,对于中序遍历,右指针为空的结点D E H F I,利用线索(红色箭头)可以直接标识出该结点的后驱;但对于右指针非空的普通的结点B、A、C、G,它的后继是右子树最左下的结点,比如B的后继结点为H,A的后继结点为F,因此,中序遍历中找后驱分为两种情况。
后序线索二叉树找后驱可分为三种情况,第一种:根结点后序为null;
第二种,如果一个结点为父结点的右孩子或父结点的左孩子(父结点没有右子树),他的后继就是父结点;比如C的后驱为A结点。
第三种,如果结点是父节点的左孩子,而且父结点有右孩子,那么后继为父结点的右子树按后序遍历列出的第一个结点。比如B结点的后继结点为F结点。
平衡二叉树
定义:一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。平衡二叉树的提出大大降低了操作的时间复杂度。
动态调平衡
LL型平衡旋转(单向右旋平衡处理)
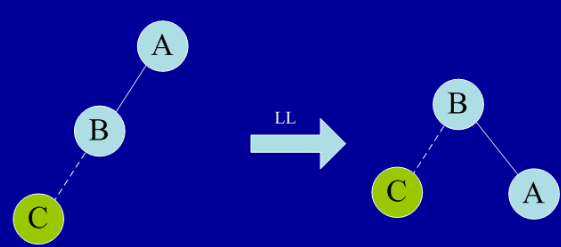
RR型平衡旋转(单向左旋转平衡处理)
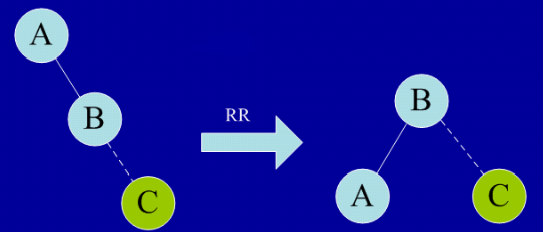
LR型平衡旋转(双向旋转,先左后右)

RL型平衡旋转(双向旋转,先右后左)

堆
再补充一个堆,其实一般所说的堆就是一棵完全二叉树。
定义:n个元素的序列{k1,k2,...,kn}当满足下列关系关系时,称为堆:
Ki <= K2i 且 Ki <= K2i+1或者Ki>=K2i且Ki>=K2i+1;
定义比较抽象,举例说明:
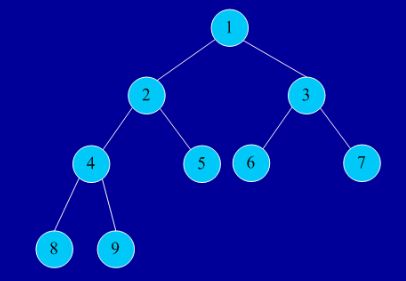
Ki <= K2i 且 Ki <= K2i+1:以上图为例,1结点 < 2结点且1结点 < 3结点,下面子树同样成立(孩子结点大于父结点),因此这类完全二叉树就被称为小根堆;
如果有一棵完全二叉树符合Ki>=K2i且Ki>=K2i+1(和上面类似,不演示例子),孩子结点小于父结点,这类二叉树被称为大根堆。
特性
对于结点i,i>=n/2时,表示结点i为叶子结点。
http://blog.csdn.net/bjyfb/article/details/7519360
http://blog.csdn.net/bjyfb/article/details/7522000
二叉树遍历实例代码
//BinaryTree.h
#ifndef BINARY_TREE_H
#define BINARY_TREE_H
#include <Windows.h>
#include <iostream>
using namespace std;
namespace BinaryTreeSpace
{
struct BinaryTreeNode
{
int nData;
BinaryTreeNode* pLeftChild;
BinaryTreeNode* pRightChild;
BinaryTreeNode()
{
nData = 0;
pLeftChild = NULL;
pRightChild = NULL;
}
};
enum EM_ORDER
{
EM_DLR = 0,
EM_LDR = 1,
EM_LRD = 2
};
class BinaryTree
{
public:
BinaryTree();
BinaryTreeNode* AddNode(int nData);
//前序遍历
void VisitTree_DLR(const BinaryTreeNode* pTree = NULL);
//中序遍历
void VisitTree_LDR(const BinaryTreeNode* pTree = NULL);
//后序遍历
void VisitTree_LRD(const BinaryTreeNode* pTree = NULL);
//打印树的信息
void PrintNode(EM_ORDER emType, const BinaryTreeNode* pNode);
//获取数的深度
int GetDepth(const BinaryTreeNode* pTree = NULL);
//获取到也节点的数量
int GetLeafCout(const BinaryTreeNode* pTree = NULL);
//获取到所有节点的数量
int GetNodeCout(const BinaryTreeNode* pTree = NULL);
const BinaryTreeNode* GetRoot() const
{
return m_pRootNode;
}
private:
BinaryTreeNode* m_pRootNode;
int m_nLeftCount;
int m_nRightCount;
int m_nTotelNode;
};
//////////////////////////////////////////////////////////////////////////
void BinaryTree_Test1();
void BinaryTree_Test2();
}
#endif
#include "BinaryTree.h"
namespace BinaryTreeSpace
{
#define GetTreeAddress(pTree) \
const BinaryTreeNode* pTemp = NULL;\
if (NULL == pTree)\
{\
pTemp = m_pRootNode;\
}\
else\
{\
pTemp = pTree;\
}\
#define PrintNodeInfo(emType) \
m_nLeftCount = 0;\
m_nRightCount = 0;\
m_nTotelNode = 0;\
PrintNode(emType, pTemp);\
cout << "\nm_LeftCount = " << m_nLeftCount << " m_RightCount = " << m_nRightCount <<" m_nTotelNode = " << m_nTotelNode << endl;\
BinaryTree::BinaryTree()
: m_pRootNode(NULL)
, m_nLeftCount(0)
, m_nRightCount(0)
, m_nTotelNode(0)
{ }
BinaryTreeNode* BinaryTree::AddNode(int nData)
{
if (NULL == m_pRootNode)
{
m_pRootNode = new BinaryTreeNode();
m_pRootNode->nData = nData;
return m_pRootNode;
}
else
{
BinaryTreeNode* pTempPtr = m_pRootNode;
BinaryTreeNode* pNewNode = new BinaryTreeNode();
pNewNode->nData = nData;
while (pTempPtr != NULL)
{
if (nData > pTempPtr->nData)
{
if (NULL == pTempPtr->pRightChild)
{
pTempPtr->pRightChild = pNewNode;
break;
}
else
{
pTempPtr = pTempPtr->pRightChild;
}
}
else
{
if (NULL == pTempPtr->pLeftChild)
{
pTempPtr->pLeftChild = pNewNode;
break;
}
else
{
pTempPtr = pTempPtr->pLeftChild;
}
}
};
return pNewNode;
}
}
void BinaryTree::VisitTree_DLR(const BinaryTreeNode* pTree)
{
cout << "前序遍历:" << endl;
GetTreeAddress(pTree);
PrintNodeInfo(EM_DLR);
}
void BinaryTree::VisitTree_LDR(const BinaryTreeNode* pTree)
{
cout << "中序遍历:" << endl;
GetTreeAddress(pTree);
PrintNodeInfo(EM_LDR);
}
void BinaryTree::VisitTree_LRD(const BinaryTreeNode* pTree)
{
cout << "后序遍历:" << endl;
GetTreeAddress(pTree);
PrintNodeInfo(EM_LRD);
}
void BinaryTree::PrintNode(EM_ORDER emType, const BinaryTreeNode* pNode)
{
if (pNode != NULL)
{
if (EM_DLR == emType)
{
m_nTotelNode++;
cout << " " << pNode->nData;
}
//Get Left Leaf
if (pNode->pLeftChild != NULL)
{
m_nLeftCount++;
PrintNode(emType, pNode->pLeftChild);
}
if (EM_LDR == emType)
{
m_nTotelNode++;
cout << " " << pNode->nData ;
}
//Get Right Leaf
if (pNode->pRightChild != NULL)
{
m_nRightCount++;
PrintNode(emType, pNode->pRightChild);
}
if (EM_LRD == emType)
{
m_nTotelNode++;
cout << " " << pNode->nData;
}
}
}
int BinaryTree::GetDepth(const BinaryTreeNode* pTree)
{
if (NULL == pTree)
{
return 0;
}
int nLeftCout = GetDepth(pTree->pLeftChild);
int nRightCout = GetDepth(pTree->pRightChild);
return (nLeftCout>nRightCout ? nLeftCout : nRightCout) + 1;
}
int BinaryTree::GetLeafCout(const BinaryTreeNode* pTree)
{
if (NULL == pTree)
{
return 0;
}
if (pTree->pLeftChild==NULL
&& pTree->pRightChild==NULL)
{
return 1;
}
return GetLeafCout(pTree->pLeftChild) + GetLeafCout(pTree->pRightChild);
}
int BinaryTree::GetNodeCout(const BinaryTreeNode* pTree)
{
if (NULL == pTree)
{
return 0;
}
return 1 + GetNodeCout(pTree->pLeftChild) + GetNodeCout(pTree->pRightChild);
}
void BinaryTree_Test1()
{
cout << "--------------------------------BinaryTree_Test1--------------------------------" << endl;
BinaryTree cBinaryTree;
BinaryTreeNode* pTemp = cBinaryTree.AddNode(1);
//////////////////////////////////////////////////////////////////////////
pTemp->pLeftChild = new BinaryTreeNode();
pTemp->pLeftChild->nData = 2;
pTemp->pLeftChild->pLeftChild = new BinaryTreeNode();
pTemp->pLeftChild->pLeftChild->nData = 4;
pTemp->pLeftChild->pRightChild = new BinaryTreeNode();
pTemp->pLeftChild->pRightChild->nData = 5;
pTemp->pLeftChild->pRightChild->pLeftChild = new BinaryTreeNode();
pTemp->pLeftChild->pRightChild->pLeftChild->nData = 7;
pTemp->pLeftChild->pRightChild->pLeftChild->pRightChild = new BinaryTreeNode();
pTemp->pLeftChild->pRightChild->pLeftChild->pRightChild->nData = 8;
//////////////////////////////////////////////////////////////////////////
pTemp->pRightChild = new BinaryTreeNode();
pTemp->pRightChild->nData = 3;
pTemp->pRightChild->pRightChild = new BinaryTreeNode();
pTemp->pRightChild->pRightChild->nData = 6;
cBinaryTree.VisitTree_DLR(pTemp);
cBinaryTree.VisitTree_LDR(pTemp);
cBinaryTree.VisitTree_LRD(pTemp);
cout << "树的深度为:" << cBinaryTree.GetDepth(pTemp) << endl;
cout << "树的节点数量为:" << cBinaryTree.GetNodeCout(pTemp) << endl;
cout << "树的叶节点数量为:" << cBinaryTree.GetLeafCout(pTemp) << endl;
cBinaryTree.VisitTree_DLR(pTemp->pLeftChild);
cBinaryTree.VisitTree_DLR(pTemp->pRightChild);
cBinaryTree.VisitTree_DLR(pTemp->pLeftChild->pRightChild);
cBinaryTree.VisitTree_DLR(pTemp->pLeftChild->pLeftChild);
}
void BinaryTree_Test2()
{
cout << "--------------------------------BinaryTree_Test2--------------------------------" << endl;
BinaryTree cBinaryTree;
int array[]={7,4,2,3,15,35,6,45,55,20,1,14,56,57,58};
for(int i = 0; i < sizeof(array)/sizeof(array[0]); i++)
{
cBinaryTree.AddNode(array[i]);
}
cBinaryTree.VisitTree_DLR(NULL);
cBinaryTree.VisitTree_LDR(NULL);
cBinaryTree.VisitTree_LRD(NULL);
cout << "树的深度为:" << cBinaryTree.GetDepth(cBinaryTree.GetRoot()) << endl;
cout << "树的节点数量为:" << cBinaryTree.GetNodeCout(cBinaryTree.GetRoot()) << endl;
cout << "树的叶节点数量为:" << cBinaryTree.GetLeafCout(cBinaryTree.GetRoot()) << endl;
}
}
#include "BinaryTree.h"
using namespace BinaryTreeSpace;
void main()
{
BinaryTree_Test1();
BinaryTree_Test2();
}
二叉树并不是一种特殊的树,是一种独立的数据结构。下面是一些关于二叉树入门级的、纯理论的东东,高手请Alt+F4,千万别往下翻,会影响您的心情!
二叉树的分类
满二叉树:除最后一层无任何子节点外,每一层上的所有结点都有两个子结点。
完全二叉树:除了最下面一层,其他层结点都是饱满的,并且最下层上的结点都集中在该层最左边的若干位置上。(满二叉树也是完全二叉树)
非完全二叉树:既不是满二叉树,也非完全二叉树。
例:

二叉树的遍历
前序遍历(先根遍历):根左右。
后序遍历(后根遍历):左右根。
中序遍历(中根遍历):左跟右。
层次遍历:一层一层自左向右。
例:

图中前序遍历结果是:1,2,4,5,7,8,3,6;
图中中序遍历结果是:4,2,7,8,5,1,3,6;
图中后序遍历结果是:4,8,7,5,2,6,3,1;
图中层次遍历结果是:1,2,3,4,5,6,7,8;
树和二叉树的转换
将树的孩子结点转成二叉树的左子结点,树的兄弟结点转成二叉树的右子结点。
例:

二叉树的一些重要特性
1、在二叉树的第i层上最多有2^(n-1)个结点(i>=1);
例:以图1为例:任一图中第2层,最多只能有2个结点。验证正确!
2、深度为k的二叉树最多有2^k - 1个结点(K>=1);
例:以图1为例:图中所有二叉树深度为3,因此,该些二叉树最多有2^3 -1 = 7个结点,验证正确!
3、对任何一颗二叉树,如果其叶子结点数为n0,度为2的结点数为n2,则n0 = n2 + 1;
例:以图1为例:看最后一个非完全二叉树,图中所示,叶子结点n0 = 2;度为2的结点n2 = 1(结点2);则2 = 1 + 1。验证正确!
4、如果对一颗有n个结点的完全二叉树的结点按层序编号(从第1层到⌊log2n⌋ + 1层,每层从左到右),则对任一结点i(1<=i<=n),(⌊⌋向下取整符号) 有:
如果i=1,则结点i无父节点,是二叉树的根;如果i>1,则父节点是⌊i/2⌋ ;
例:
以图1左侧的完全二叉树为例:若i = 3,则i > 1,⌊3/2⌋ = 1,3的根结点为1。验证 正确!
如果2i>n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i;
例:
以图1左侧的完全二叉树为例:若i = 3,因 n = 5,则2i>n,由此推出3为叶子结点。若i = 2,因 n = 5,则2i<n,由此推出2的左子结点为4。验证正确!
如果2i+1>n,则结点i无右子结点,否则,其右子结点是结点2i + 1。
例:
以图1左侧的完全二叉树为例:上一条否命题求出了左子树结点,而这条正好求出了右子树结点。结点i=2的右子树结点为5,验证正确!
查找二叉树(二叉排序树)
二叉排序树(Binary Sort Tree)又称二叉查找树(Binary Search Tree)。其定义为:二叉排序树或者是空树,或者是满足如下性质的二叉树:
①若它的左子树非空,则左子树上所有结点的值均小于根结点的值;
②若它的右子树非空,则右子树上所有结点的值均大于根结点的值;
③左、右子树本身又各是一棵二叉排序树。
例:

对排序二叉树的一些操作
查找:若根结点的关键字值等于查找的关键字,成功。
否则,若小于根结点的关键字值,递归查左子树。
若大于根结点的关键字值,递归查右子树。
若子树为空,查找不成功。
插入:分以下几种情况进行相应的处理:
①如果相同键值的结点已在查找二叉树中,则不再插入;
②如果查找二叉树为空树,则以新结点为查找二叉树;
③将要插入结点的键值与插入后的父结点的键值比较,就能确定新结点是父结点的左子结点,还是右子结点,并进行相应插入,新插入的结点一定是一个新添加的叶子结点。
删除:分以下几种情况进行相应的处理:
①若待删除的结点p是叶子结点,则直接删除该结点;
②若待删除的结点p只有一个子节点,则将这个子结点与待删除结点的父结点直接连接,然后删除节点p;
③若待删除的结点p有两个子结点,则在其左子树上,用中序遍历寻找关健值最大的结点s,用结点s的值代替结点p的值,然后删除节点s,结点s必属于上述①、②情况之一。
例:删除图1中的根结点5
首先,中序遍历结点5的左子树,获得最大的结点s=4,将p=5和s=4互换位置,发现要删除的p结点属于第①种情况,则直接删除p=5结点。
最优二叉树(哈夫曼树)
最优二叉树是带权路径长度最小的树。
基本术语
树的路径长度:是从树根到树中每一个结点的路径长度之和。在结点数目相同的二叉树中,完全二叉树的路径长度最短。
结点的权:根据应用的需要给树的结点赋的权值。
带权路径长度:结点到树根之间的路径长度与该结点上权的乘积,称为结点的带权路径长度。
树的带权路径长度(树的代价):树中所有叶结点的带权路径长度之和,称为树的代价。
构造哈夫曼树

哈弗曼编码
求出哈夫曼树后,以上图为例,只需人为规定左侧为0,右侧为1,那么结点23的编码是:00;结点11的编码是:010。哈夫曼编码是一种应用广泛且非常有效的数据压缩技术,该技术一般可将数据文件压缩掉20%-90%,其压缩效率取决于被压缩文件的特征。
线索二叉树
二叉树的遍历本质上是将一个复杂的非线性结构转换为线性结构,使每个结点都有了唯一前驱和后继(第一个结点无前驱,最后一个结点无后继)。对于二叉树的一个结点,查找其左右子女是方便的,其前驱后继只有在遍历中得到。为了容易找到前驱和后继,有两种方法。一是在结点结构中增加向前和向后的指针fwd和bkd,这种方法增加了存储开销,不可取;二是利用二叉树的空链指针。现将二叉树的结点结构重新定义如下:

对于标志域规定如下:
Lbit=0,Lchild是通常的指正;Lbit=1,Lchild是线索;
Rbit=0,Rchild是通常的指针;Rbit=1,Rchild是线索;
将二叉树转化为线索二叉树
第一步:将将二叉树的前序遍历、中序遍历、后序遍历的顺序写下来;
下图前序遍历顺序:A B D E H C F G I
中序遍历:D B H E A F C G I
后序遍历:D H E B F I G C A
第二步:参照遍历的顺序,找到各个结点对应的前驱和后驱,如下图:

绿色线表示前驱;红色线表示后驱。
上面提到线索二叉树的使用就是为了方便的找到前驱和后驱,对于中序遍历,右指针为空的结点D E H F I,利用线索(红色箭头)可以直接标识出该结点的后驱;但对于右指针非空的普通的结点B、A、C、G,它的后继是右子树最左下的结点,比如B的后继结点为H,A的后继结点为F,因此,中序遍历中找后驱分为两种情况。
后序线索二叉树找后驱可分为三种情况,第一种:根结点后序为null;
第二种,如果一个结点为父结点的右孩子或父结点的左孩子(父结点没有右子树),他的后继就是父结点;比如C的后驱为A结点。
第三种,如果结点是父节点的左孩子,而且父结点有右孩子,那么后继为父结点的右子树按后序遍历列出的第一个结点。比如B结点的后继结点为F结点。
平衡二叉树
定义:一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。平衡二叉树的提出大大降低了操作的时间复杂度。
动态调平衡
LL型平衡旋转(单向右旋平衡处理)

RR型平衡旋转(单向左旋转平衡处理)

LR型平衡旋转(双向旋转,先左后右)

RL型平衡旋转(双向旋转,先右后左)

堆
再补充一个堆,其实一般所说的堆就是一棵完全二叉树。
定义:n个元素的序列{k1,k2,...,kn}当满足下列关系关系时,称为堆:
Ki <= K2i 且 Ki <= K2i+1或者Ki>=K2i且Ki>=K2i+1;
定义比较抽象,举例说明:

Ki <= K2i 且 Ki <= K2i+1:以上图为例,1结点 < 2结点且1结点 < 3结点,下面子树同样成立(孩子结点大于父结点),因此这类完全二叉树就被称为小根堆;
如果有一棵完全二叉树符合Ki>=K2i且Ki>=K2i+1(和上面类似,不演示例子),孩子结点小于父结点,这类二叉树被称为大根堆。
特性
对于结点i,i>=n/2时,表示结点i为叶子结点。
- 常用数据结构--线性结构_二叉树.zip (1.2 MB)
- 下载次数: 0
- BinaryTree.zip (2 KB)
- 下载次数: 0
发表评论
-
FreeRTOS
2022-03-05 16:31 266Ref https://blog.csdn.net/weix ... -
串口通讯相关
2018-11-02 13:44 431https://bbs.csdn.net/wap/topics ... -
[转]C++验证IP是否可以PING通
2018-10-30 17:54 1369https://www.cnblogs.com/guoyz13 ... -
C++/MFC 換皮膚
2018-10-20 11:05 497https://blog.csdn.net/u01123991 ... -
WinCE 截屏 - C++ 代碼
2018-08-31 09:45 598// this function create a bmp ... -
Android NDK搭建環境
2017-11-27 13:25 620https://www.cnblogs.com/ut2016- ... -
8583协议相关
2017-10-17 13:38 6098583相关资料,整理中... -
Java高级应用之JNI
2017-06-19 09:00 619参考link http://www.cnblogs.com/l ... -
C++实现ping功能
2017-04-18 11:21 2210基础知识 ping的过程是向目的IP发送一个type=8的I ... -
OpenSSL 编译环境搭建
2017-03-27 15:01 9311 安裝VS2008到 c:\Program Files (x ... -
最优非对称加密填充(OAEP)
2017-03-25 14:53 1624OpenSSL命令---rsautl http://blog. ... -
[Platform Builder] 设置SVM OS build Env
2016-11-10 11:39 01 copy one OSDesign Project to ... -
[Windows] System Error Codes(GetLastError )0-----5999
2016-10-26 13:28 1899ERROR_SUCCESS 0 (0x0) T ... -
开源Windows驱动程序框架
2016-09-17 21:35 898转自 http://code.csdn.net/news/28 ... -
c/c++代码中执行cmd命令
2016-09-14 14:50 1950转自 http://blog.csdn.net/slixinx ... -
C#使用C++标准DLL实例(包含callback)
2016-09-11 19:44 1115C++编写标准Win32DLL如下 头文件 /***** ... -
C#调用C++的DLL搜集整理的所有数据类型转换方式
2016-09-09 16:07 991转自 http://www.cnblogs.com/zeroo ... -
WinCE CPU使用率计算 测试工具
2016-09-08 16:14 1034转自 http://blog.csdn.net/jan ... -
switch在C++与C#中的一些差异
2016-09-08 15:19 842参考链接 http://blog.csdn.net/weiwe ... -
C++ 鼠标模拟程序
2016-09-04 12:09 1641转自 http://blog.csdn.net/weixinh ...





相关推荐
二叉树是计算机科学中一种重要的数据结构,它在很多算法和问题解决中都有广泛应用,尤其是在数据存储和检索领域。二叉树的概念源自于它的基本结构:每个节点最多有两个子节点,通常分为左子节点和右子节点。这种特殊...
二叉树是计算机科学中一种重要的数据结构,它在很多算法和问题解决中扮演着核心角色。本资料主要探讨了二叉树的基本算法,包括如何建立二叉树、三种主要的遍历方法(前序、中序、后序)以及递归与非递归的应用,还有...
### 数据结构与算法(C#实现)系列---二叉树 #### 概述 本文档将详细介绍二叉树这一重要的...二叉树作为一种常用的数据结构,在实际开发中有着广泛的应用。理解并掌握二叉树的实现可以帮助开发者更好地解决复杂问题。
### Java常用数据结构详解 #### 一、线性表(顺序表) 线性表是数据结构中最基础的数据组织形式之一,通常分为顺序表和链表两种实现方式。本部分主要介绍顺序表,即通过数组来实现的一种线性表。 ##### 1. 顺序表...
数据结构中的二叉树是一种非线性数据结构,它由n(n>=0)个有限节点组成,每个节点最多有两个子节点,分别称为左子节点和右子节点。在这个问题中,二叉树被实现为二叉链表,其中每个节点包含一个数据元素和两个指向...
二叉树是一种常用的数据结构,广泛应用于计算机科学和信息技术领域。在本文中,我们将讨论二叉树的路径问题,并提供一个解决方案来找到二叉树根节点到叶节点的路径。 1. 数据结构 - 二叉树 二叉树是一种树形数据...
### 数据结构名词解释详解 #### 1. 数据 数据是对客观事物进行描述的符号,能够被计算机识别、处理。在计算机科学中,数据是信息化的基础,涵盖了文本、图像、音频等多种形式。 #### 2. 数据项 数据项是数据中不可...
### 数据结构与算法-二叉树的排序 #### 一、二叉树的基本概念与表示 二叉树是一种非线性的数据结构,每个节点最多有两个子节点,通常这两个子节点被称作左子节点和右子节点。在计算机科学中,二叉树经常用于构建...
数据结构中的二叉树是一种非常重要的抽象数据类型,它由结点构成,每个结点最多有两个子结点,通常称为左子结点和右子结点。在这个实验报告中,我们将深入探讨二叉树的存储实现、遍历方法以及相关的算法实现。 首先...
根据提供的文件信息,我们可以总结出以下关于“数据结构C语言二叉树实验代码”的相关知识点: ### 一、二叉树的基本概念 **二叉树(Binary Tree)**是一种非线性的数据结构,在计算机科学中有着广泛的应用。二叉树中...
在计算机科学中,**树(Tree)**是一种常用的数据结构,它由一系列结点组成,这些结点之间通过边连接,形成一种层次关系。树中的每个结点都可以有零个或多个子结点。树通常有一个特殊的结点,称为**根结点**,没有父...
数据结构是计算机科学中的核心课程,它探讨了如何在计算机中高效地组织和管理数据,以便于进行快速的检索、存储和处理。殷人昆教授的《数据结构》教材是这个领域的经典之作,广泛用于教学和自学。PPT形式的教材通常...
本教程“现代计算机常用数据结构和算法”旨在帮助学习者深入理解这些概念,并提升其编程能力。 数据结构主要包括数组、链表、栈、队列、树、图、哈希表等。数组是最基本的数据结构,它提供了一种方式来存储和访问...
这个大作业旨在让学生深入理解数据结构中的平衡二叉树原理,并能用Java这一常用编程语言实现相关算法。通过这个过程,学生不仅可以提升编程能力,还能掌握解决实际问题的方法,为今后的软件开发工作打下坚实基础。
数据结构是计算机科学中的核心课程,它探讨了如何在计算机中高效地组织和管理数据,以便进行快速查找、插入和删除等操作。唐发根版的数据结构PPT教程以其深入浅出的方式,为学习者提供了丰富的知识资源。下面将详细...
数据结构是计算机科学中的核心概念,它涉及到如何在内存中高效地组织和管理数据,以便进行快速检索、插入和删除等操作。严蔚敏教授编写的《数据结构--C语言描述》是一本经典教材,广泛应用于高校计算机专业教学。...
8. **递归与分治策略**:递归是数据结构中常用的思想,如二分查找、归并排序等。分治策略如快速排序、归并排序、大整数乘法等,能提高问题的解题效率。 9. **动态规划**:解决复杂问题的一种方法,如最短路径、背包...
3. **数据结构**:数组、链表、栈、队列、树(二叉树、AVL树、红黑树等)、图、散列表(哈希表)等,这些都是编程中常用的基础结构,它们各自有独特的特性和用途。 4. **递归与分治**:递归算法如斐波那契数列、...