Σ╕אπאבµ¡úµץ┤µץ░τתהσםבΦ┐¢σט╢Φ╜¼µםóΣ║לΦ┐¢σט╢∩╝ת
Φªבτג╣∩╝תΘשñΣ║לσןצΣ╜ש∩╝לσאעσ║ןµמעσטק
ΦºúΘחך∩╝תσ░זΣ╕אΣ╕¬σםבΦ┐¢σט╢µץ░ΘשñΣ╗ÑΣ║ל∩╝לσ╛קσט░τתהσץזσזםΘשñΣ╗ÑΣ║ל∩╝לΣ╛¥µ¡ñτ▒╗µמ¿τ¢┤σט░σץזτ¡יΣ║מΣ╕אµטצΘ¢╢µק╢Σ╕║µ¡ó∩╝לσאעσןצσ░זΘשñσ╛קτתהΣ╜שµץ░∩╝לσם│µםóτ«קΣ╕║Σ║לΦ┐¢σט╢µץ░τתהτ╗ףµ₧£
Σ╛כσªגµךך52µםóτ«קµטנΣ║לΦ┐¢σט╢µץ░∩╝לΦ«íτ«קτ╗ףµ₧£σªגσ¢╛∩╝ת
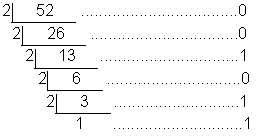
52ΘשñΣ╗Ñ2σ╛קσט░τתהΣ╜שµץ░Σ╛¥µ¼íΣ╕║∩╝ת0πאב0πאב1πאב0πאב1πאב1∩╝לσאעσ║ןµמעσטק∩╝לµיאΣ╗Ñ52σ»╣σ║פτתהΣ║לΦ┐¢σט╢µץ░σ░▒µר»110100πאג
τפ▒Σ║מΦ«íτ«קµ£║σזוΘד¿Φí¿τñ║µץ░τתהσ¡קΦךגσםץΣ╜םΘד╜µר»σ«תΘץ┐τתה∩╝לΣ╗Ñ2τתהσ╣גµ¼íσ▒ץσ╝א∩╝לµטצΦאו8Σ╜ם∩╝לµטצΦאו16Σ╜ם∩╝לµטצΦאו32Σ╜ם....πאג
Σ║מµר»∩╝לΣ╕אΣ╕¬Σ║לΦ┐¢σט╢µץ░τפ¿Φ«íτ«קµ£║Φí¿τñ║µק╢∩╝לΣ╜םµץ░Σ╕םΦ╢│2τתהσ╣גµ¼íµק╢∩╝לΘ½רΣ╜םΣ╕ךΦªבΦíÑΦ╢│ΦכÑσ╣▓Σ╕¬0πאגµ£¼µצחΘד╜Σ╗Ñ8Σ╜םΣ╕║Σ╛כπאגΘגúΣ╣ט∩╝ת
(52)10=(00110100)2
Σ║לπאבΦ┤ƒµץ┤µץ░Φ╜¼µםóΣ╕║Σ║לΦ┐¢σט╢
Φªבτג╣∩╝תσןצσןםσךáΣ╕א
ΦºúΘחך∩╝תσ░זΦ»ÑΦ┤ƒµץ┤µץ░σ»╣σ║פτתהµ¡úµץ┤µץ░σוטΦ╜¼µםóµטנΣ║לΦ┐¢σט╢∩╝לτה╢σנמσ»╣σו╢Γא£σןצΦíÑΓא¥∩╝לσזםσ»╣σןצΦíÑσנמτתהτ╗ףµ₧£σךá1σם│σן»
Σ╛כσªגΦªבµךך-52µםóτ«קµטנΣ║לΦ┐¢σט╢∩╝ת
1.σוטσןצσ╛ק52τתהΣ║לΦ┐¢σט╢∩╝ת00110100
2.σ»╣µיאσ╛קσט░τתהΣ║לΦ┐¢σט╢µץ░σןצσןם∩╝ת11001011
3.σ░זσןצσןםσנמτתהµץ░σא╝σךáΣ╕אσם│σן»∩╝ת11001100
σם│∩╝ת(-52)10=(11001100)2
Σ╕יπאבσ░ןµץ░Φ╜¼µםóΣ╕║Σ║לΦ┐¢σט╢
Φªבτג╣∩╝תΣ╣רΣ║לσןצµץ┤∩╝לµ¡úσ║ןµמעσטק
ΦºúΘחך∩╝תσ»╣Φó½Φ╜¼µםóτתהσ░ןµץ░Σ╣רΣ╗Ñ2∩╝לσןצσו╢µץ┤µץ░Θד¿σטז(0µטצ1)Σ╜£Σ╕║Σ║לΦ┐¢σט╢σ░ןµץ░Θד¿σטז∩╝לσןצσו╢σ░ןµץ░Θד¿σטז∩╝לσזםΣ╣רΣ╗Ñ2∩╝לσןטσןצσו╢µץ┤µץ░Θד¿σטזΣ╜£Σ╕║Σ║לΦ┐¢σט╢σ░ןµץ░Θד¿σטז∩╝לτה╢σנמσןצσ░ןµץ░Θד¿σטז∩╝לσזםΣ╣רΣ╗Ñ2∩╝לτ¢┤σט░σ░ןµץ░Θד¿σטזΣ╕║0µטצΦאוσ╖▓τ╗ןσמ╗σט░Σ║זΦ╢│σñƒΣ╜םµץ░πאגµ»ןµ¼íσןצτתהµץ┤µץ░Θד¿σטז∩╝לµליσוטσנמµ¼íσ║ןµמעσטק∩╝לσ░▒µ₧הµטנΣ║זΣ║לΦ┐¢σט╢σ░ןµץ░τתהσ║ןσטק
Σ╛כσªגµךך0.2Φ╜¼µםóΣ╕║Σ║לΦ┐¢σט╢∩╝לΦ╜¼µםóΦ┐חτ¿כσªגσ¢╛∩╝ת
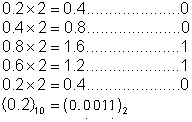
0.2Σ╣רΣ╗Ñ2∩╝לσןצµץ┤σנמσ░ןµץ░Θד¿σטזσזםΣ╣רΣ╗Ñ2∩╝לΦ┐נτ«ק4µ¼íσנמσ╛קσט░τתהµץ┤µץ░Θד¿σטזΣ╛¥µ¼íΣ╕║0πאב0πאב1πאב1∩╝לτ╗ףµ₧£σןטσןרµטנΣ║ז0.2∩╝ל
Φכѵ₧£0.2σזםΣ╣רΣ╗Ñ2σנמΣ╝תσ╛¬τמ»σטתσ╝אσºכτתה4µ¼íΦ┐נτ«ק∩╝לµיאΣ╗Ñ0.2Φ╜¼µםóΣ║לΦ┐¢σט╢σנמσ░זµר»0011τתהσ╛¬τמ»∩╝לσם│∩╝ת
(0.2)10=(0.0011 0011 0011 .....)2
σ╛¬τמ»τתהΣ╣ªσזשµצ╣µ│ץΣ╕║σ£¿σ╛¬τמ»σ║ןσטקτתהτ¼¼Σ╕אΣ╜םσעלµ£אσנמΣ╕אΣ╜םσטזσט½σךáΣ╕אΣ╕¬τג╣µáחµ│¿
σ¢¢πאבΣ║לΦ┐¢σט╢Φ╜¼µםóΣ╕║σםבΦ┐¢σט╢∩╝ת
 
µץ┤µץ░Σ║לΦ┐¢σט╢τפ¿µץ░σא╝Σ╣רΣ╗Ñ2τתהσ╣גµ¼íΣ╛¥µ¼íτ¢╕σךá∩╝לσ░ןµץ░Σ║לΦ┐¢σט╢τפ¿µץ░σא╝Σ╣רΣ╗Ñ2τתהΦ┤ƒσ╣גµ¼íτה╢σנמΣ╛¥µ¼íτ¢╕σךá∩╝ב
µ»פσªגσ░זΣ║לΦ┐¢σט╢110Φ╜¼µםóΣ╕║σםבΦ┐¢σט╢∩╝ת
ΘªצσוטΦíÑΘ╜נΣ╜םµץ░∩╝ל00000110∩╝לΘªצΣ╜םΣ╕║0∩╝לσטשΣ╕║µ¡úµץ┤µץ░∩╝לΘגúΣ╣טσ░זΣ║לΦ┐¢σט╢Σ╕¡τתהΣ╕יΣ╜םµץ░σטזσט½Σ║מΣ╕כΦ╛╣σ»╣σ║פτתהσא╝τ¢╕Σ╣רσנמτ¢╕σךáσ╛קσט░τתהσא╝Σ╕║µםóτ«קΣ╕║σםבΦ┐¢σט╢τתהτ╗ףµ₧£
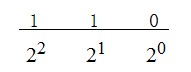

σªגµ₧£Σ║לΦ┐¢σט╢µץ░ΦíÑΦ╢│Σ╜םµץ░Σ╣כσנמΘªצΣ╜םΣ╕║1∩╝לΘגúΣ╣טσו╢σ»╣σ║פτתהµץ┤µץ░Σ╕║Φ┤ƒ∩╝לΘגúΣ╣טΘ£אΦªבσוטσןצσןםτה╢σנמσזםµםóτ«ק
µ»פσªג11111001∩╝לΘªצΣ╜םΣ╕║1∩╝לΘגúΣ╣טΘ£אΦªבσוטσ»╣σו╢σןצσןם∩╝לσם│∩╝ת-00000110
00000110,σ»╣σ║פτתהσםבΦ┐¢σט╢Σ╕║6∩╝לσ¢áµ¡ñ11111001σ»╣σ║פτתהσםבΦ┐¢σט╢σם│Σ╕║-6
µםóτ«קσו¼σ╝ןσן»Φí¿τñ║Σ╕║:
11111001=-00000110
              =-6
σªגµ₧£σ░זΣ║לΦ┐¢σט╢0.110Φ╜¼µםóΣ╕║σםבΦ┐¢σט╢∩╝ת
σ░זΣ║לΦ┐¢σט╢Σ╕¡τתהΣ╕יΣ╜םµץ░σטזσט½Σ║מΣ╕כΦ╛╣σ»╣σ║פτתהσא╝τ¢╕Σ╣רσנמτ¢╕σךáσ╛קσט░τתהσא╝Σ╕║µםóτ«קΣ╕║σםבΦ┐¢σט╢τתהτ╗ףµ₧£


σמƒµצח∩╝תhttp://52cpp.5d6d.com/thread-22-1-1.html
 
Φ╜¼Φח¬∩╝תσ¢╛µצחσ╣╢Φלג: Σ║לΦ┐¢σט╢Σ╕מσםבΦ┐¢σט╢Θק┤τתהΦ╜¼µםóµצ╣µ│ץ
 
 
 
 
 
 
 






τ¢╕σו│µמ¿Φםנ
2. **σםבΦ┐¢σט╢Φ╜¼µםóΣ╕║pΦ┐¢σט╢** (`ten_to_p`) ```cpp string ten_to_p(int nums, int p) { string res; while(nums) { int t = nums % p; if(t ) res.push_back(t + '0'); else res.push_back(t - 10 + 'A');...
Φ┐שτºםσ░ז32Σ╜םΣ║לΦ┐¢σט╢µץ░Φ╜¼σלצΣ╕║4Σ╕¬σו½Σ╜םΣ║לΦ┐¢σט╢µץ░σזםΦ╜¼µםóµטנσםבΦ┐¢σט╢τתהσ╜óσ╝ן∩╝לµר»Σ╕║Σ║זΣ╛┐Σ║מΣ║║τ▒╗Φ«░σ┐זσעלµףםΣ╜£πאג σ£¿σ«₧Θשוµץשσ¡ªΣ╕¡∩╝לσ¡ªτפƒΘ£אΦªבµמלµןíσםבΦ┐¢σט╢σעלΣ║לΦ┐¢σט╢Σ╣כΘק┤τתהΦ╜¼µםóπאגΣ╛כσªג∩╝לσ░זσםבΦ┐¢σט╢µץ░34Φ╜¼µםóΣ╕║Σ║לΦ┐¢σט╢µץ░∩╝לσן»Σ╗ÑΣ╜┐τפ¿τƒ¡Θשñµ│ץ∩╝לσם│34ΘשñΣ╗Ñ2...
2. **Σ║לΦ┐¢σט╢µץ░σט╢**∩╝תΦ»ªτ╗זΦ«▓ΦºúΣ║לΦ┐¢σט╢µץ░σט╢∩╝לσלוµכ¼Σ║לΦ┐¢σט╢µץ░τתהΦí¿τñ║πאבΦ┐נτ«קΦºהσטש∩╝טσªגσךáµ│ץπאבσחןµ│ץ∩╝יπאבΣ║לΦ┐¢σט╢Σ╕מσםבΦ┐¢σט╢Σ╣כΘק┤τתהΦ╜¼µםóπאג 3. **σו╢Σ╗צµץ░σט╢**∩╝תµי⌐σ▒ץσט░σו½Φ┐¢σט╢πאבσםבσו¡Φ┐¢σט╢τ¡יσ╕╕τפ¿µץ░σט╢∩╝לσ╣╢ΦºúΘחךσו╢σ£¿Φ«íτ«קµ£║Σ╕¡τתהσ║פτפ¿πאג 4. **Σ╜ם...
Θªצσוט∩╝לµטסΣ╗¼Σ╝תσ¢₧Θí╛σםבΦ┐¢σט╢µץ░σט╢∩╝לτה╢σנמσ╝ץσוÑΣ║לΦ┐¢σט╢∩╝לΘאתΦ┐חΣ║עσך¿σ╝ןµ╝פτñ║∩╝לΦ«⌐σ¡ªτפƒσ░¥Φ»ץσ░זσםבΦ┐¢σט╢µץ░Φ╜¼µםóΣ╕║Σ║לΦ┐¢σט╢πאגµ¡ñσñצ∩╝לΦ┐רΣ╝תΦ«¿Φ«║Σ║לΦ┐¢σט╢σ£¿Φ«íτ«קµ£║Σ╕¡τתהΘחםΦªבµאº∩╝לΣ╛כσªגσ£¿σ¡רσג¿σעלσñהτנזµץ░µם«µק╢τתהΦºעΦי▓πאגΘאתΦ┐חσ«לµטנΣ╕אΣ║¢τ╗דΣ╣áΘóר∩╝לσ¡ªτפƒσן»Σ╗ѵמלµןíσƒ║µ£¼...
2. µץ░µם«Φí¿τñ║Σ╕מΦ┐נτ«ק∩╝תµ╢╡τ¢צΣ║לΦ┐¢σט╢πאבσו½Φ┐¢σט╢πאבσםבσו¡Φ┐¢σט╢σעלσםבΦ┐¢σט╢Σ╣כΘק┤τתהΦ╜¼µםó∩╝לΣ╗ÑσןךΣ║לΦ┐¢σט╢τ╝צτáב∩╝טσªגASCIIτáבσעלµ▒יσ¡קτ╝צτáב∩╝יσעלµץ░σא╝Φ┐נτ«קτתהΣ║לΦ┐¢σט╢Φí¿τñ║µ│ץπאג 3. Θא╗Φ╛סΘק¿Σ╕מτ╗הσנטΘא╗Φ╛סτפ╡Φ╖»∩╝תΣ╗כτ╗םσƒ║µ£¼τתהΘא╗Φ╛סΘק¿∩╝טΣ╕מΘק¿πאבµטצΘק¿πאבΘ¥₧Θק¿πאבσ╝גµטצΘק¿...
Σ║לΦ┐¢σט╢µץ░Φ╜¼µםó∩╝תΣ║לΦ┐¢σט╢µץ░100101Φ╜¼µםóΣ╕║σםבΦ┐¢σט╢Σ╕║434.578125∩╝לΦ╜¼µםóΣ╕║σםבσו¡Φ┐¢σט╢Σ╕║1B2.94πאג\n\n**τ«אτ¡פΘóרΦºúµ₧נ**∩╝ת\n\n1. Φ«íτ«קµ£║τ╗הµטנΘד¿σטז∩╝תσלוµכ¼Φ┐נτ«קσש¿∩╝טΦ┤ƒΦ┤úµץ░µם«σñהτנז∩╝יπאבσ¡רσג¿σש¿∩╝טσ¡רσג¿µץ░µם«σעלµלחΣ╗ñ∩╝יπאבµמºσט╢σש¿∩╝טσםןΦ░דµץ┤Σ╕¬Φ«íτ«קµ£║...
28. **Σ║לΦ┐¢σט╢Σ╕מσםבΦ┐¢σט╢Φ╜¼µםó**∩╝תΣ║לΦ┐¢σט╢µץ░01100100τ¡יΣ║מσםבσו¡Φ┐¢σט╢µץ░64πאג 29. **Windows XPΣ╗╗σךíµáן**∩╝תµר╛τñ║σ╖▓σנ»σך¿σ╣╢µ¡úσ£¿µיºΦíלτתהτ¿כσ║ןσנם∩╝לσן»Σ╗Ñσ┐½Θאƒσטחµםóπאג 30. **Wordµץ░µם«ΘאןΦºזΦí¿**∩╝תWordΦí¿µá╝Σ╕¡Σ╕םΦד╜τ¢┤µמÑσט¢σ╗║µץ░µם«ΘאןΦºזΦí¿∩╝לΣ╜זσן»Σ╗Ñ...
2. **Σ║לΦ┐¢σט╢Σ╕מµץ░σט╢Φ╜¼µםó**∩╝תΦ«▓ΦºúΣ║לΦ┐¢σט╢πאבσו½Φ┐¢σט╢πאבσםבΦ┐¢σט╢σעלσםבσו¡Φ┐¢σט╢Σ╣כΘק┤τתהΦ╜¼µםó∩╝לΦ┐שµר»τנזΦºúΦ«íτ«קµ£║µץ░µם«Φí¿τñ║τתהσƒ║τíאπאג 3. **Θא╗Φ╛סΘק¿τפ╡Φ╖»**∩╝תΘרנΦ┐░σƒ║µ£¼τתהΘא╗Φ╛סΘק¿∩╝טσªגΣ╕מΘק¿πאבµטצΘק¿πאבΘ¥₧Θק¿∩╝יσןךσו╢τ╗הσנט∩╝לΣ╕║τנזΦºúµץ░σ¡קΘא╗Φ╛סσעלΦ«íτ«קµ£║τí¼Σ╗╢...
3. **Σ║לΦ┐¢σט╢σעלµץ░σט╢Φ╜¼µםó**∩╝תΦ«íτ«קµ£║τ│╗τ╗ƒΣ╗ÑΣ║לΦ┐¢σט╢Σ╕║σƒ║τíא∩╝לσ¢áµ¡ñτנזΦºúΣ║לΦ┐¢σט╢πאבσו½Φ┐¢σט╢πאבσםבΦ┐¢σט╢σעלσםבσו¡Φ┐¢σט╢Σ╣כΘק┤τתהΦ╜¼µםóΦח│σו│ΘחםΦªבπאגµ¡ñσñצ∩╝לσ¡ªτפƒΣ╗¼Φ┐רσ░זσ¡ªΣ╣áΣ║לΦ┐¢σט╢τ«קµ£»Φ┐נτ«ק∩╝לσªגσךáσחןΣ╣רΘשñπאג 4. **σ¡רσג¿σש¿σעלσ»הσ¡רσש¿**∩╝תΦ«íτ«קµ£║σזוσ¡רτפ▒σñºΘחן...
1. **µץ░µם«Φí¿τñ║**∩╝תΣ║לΦ┐¢σט╢πאבσו½Φ┐¢σט╢πאבσםבΦ┐¢σט╢σעלσםבσו¡Φ┐¢σט╢τתהΦ╜¼µםó∩╝לΣ╗Ñσןךµ╡«τג╣µץ░πאבΦíÑτáבπאבσמƒτáבσעלσןםτáבτתהµªגσ┐╡πאג 2. **Φ┐נτ«קσש¿**∩╝תσךáµ│ץσש¿πאבσחןµ│ץσש¿πאבΣ╣רµ│ץσש¿σעלΘשñµ│ץσש¿τתהσ╖ÑΣ╜£σמƒτנז∩╝לΣ╗Ñσןךτ«קµ£»Θא╗Φ╛סσםץσוד∩╝טALU∩╝יτתהσךƒΦד╜πאג 3. **µמºσט╢σש¿**∩╝ת...
6. Σ║לΦ┐¢σט╢σעלµץ░σט╢Φ╜¼µםó∩╝תΣ╗כτ╗םΣ║לΦ┐¢σט╢πאבσו½Φ┐¢σט╢πאבσםבΦ┐¢σט╢σעלσםבσו¡Φ┐¢σט╢Σ╣כΘק┤τתהΦ╜¼µםó∩╝לΣ╗ÑσןךΣ║לΦ┐¢σט╢ΦíÑτáבΦí¿τñ║µ│ץπאג 7. Θא╗Φ╛סτפ╡Φ╖»σƒ║τíא∩╝תσ╕דσ░פΣ╗úµץ░πאבτ╗הσנטΘא╗Φ╛סτפ╡Φ╖»σעלµק╢σ║ןΘא╗Φ╛סτפ╡Φ╖»τתהΦ«╛Φ«í∩╝לσªגΣ╕מΘק¿πאבµטצΘק¿πאבΘ¥₧Θק¿πאבΦ»סτáבσש¿πאבσ»הσ¡רσש¿τ¡יπאג 8. ...
2. µץ░σט╢Φ╜¼µםóΣ╕מτ╝צτáב∩╝תΦ«▓ΦºúΣ║לΦ┐¢σט╢πאבσו½Φ┐¢σט╢πאבσםבσו¡Φ┐¢σט╢Σ╗Ñσןךσ«דΣ╗¼Σ╕מσםבΦ┐¢σט╢Σ╣כΘק┤τתהΦ╜¼µםó∩╝לσנלµק╢µ╢יσןךASCIIτáבπאבBCDτáבτ¡יτ╝צτáבµצ╣σ╝ןπאג 3. CPUτ╗ףµ₧הΣ╕מσ╖ÑΣ╜£σמƒτנז∩╝תµ╖▒σוѵמóΦ«¿CPUτתהσזוΘד¿τ╗ףµ₧ה∩╝לσªגΦ┐נτ«קσש¿πאבµמºσט╢σש¿πאבσ»הσ¡רσש¿τ¡י∩╝לΣ╗ÑσןךµלחΣ╗ñτ│╗τ╗ƒσעל...
1. **µץ░µם«Φí¿τñ║Σ╕מΦ┐נτ«ק**∩╝תσלוµכ¼Σ║לΦ┐¢σט╢πאבσו½Φ┐¢σט╢πאבσםבΦ┐¢σט╢σעלσםבσו¡Φ┐¢σט╢Σ╣כΘק┤τתהΦ╜¼µםó∩╝לΣ║לΦ┐¢σט╢ΦíÑτáבΦí¿τñ║µ│ץτפ¿Σ║מµץ┤µץ░Φ┐נτ«ק∩╝לµ╡«τג╣µץ░Φí¿τñ║σןךΦ┐נτ«קΦºהσטש∩╝לΣ╗Ñσןךσנהτºםτ«קµ£»σעלΘא╗Φ╛סΦ┐נτ«קτ¼ªτתהτí¼Σ╗╢σ«₧τמ░πאג 2. **Φ«íτ«קµ£║τ│╗τ╗ƒτתהσ▒גµ¼íτ╗ףµ₧ה**∩╝תΣ╗מσ╛«µ₧╢µ₧הσט░...
2. **µץ░µם«Φí¿τñ║Σ╕מΦ┐נτ«ק**∩╝תΦ«▓ΦºúΣ║לΦ┐¢σט╢πאבσו½Φ┐¢σט╢πאבσםבσו¡Φ┐¢σט╢σעלσםבΦ┐¢σט╢Σ╣כΘק┤τתהΦ╜¼µםó∩╝לΣ╗Ñσןךµ╡«τג╣µץ░τתהΦí¿τñ║µצ╣µ│ץ∩╝טσªגIEEE754µáחσחז∩╝יπאגµ¡ñσñצ∩╝לΦ┐רΣ╝תµ╢יσןךτ«קµ£»Θא╗Φ╛סσםץσוד∩╝טALU∩╝יτתהΦ┐נτ«קσךƒΦד╜∩╝לσªגσךáσחןΣ╣רΘשñπאבτº╗Σ╜םσעלµ»פΦ╛דτ¡יπאג 3. **µלחΣ╗ñτ│╗τ╗ƒ**∩╝ת...
Σ╛כσªג∩╝לΣ║לΦ┐¢σט╢µץ░∩╝ט101.01∩╝י2τ¡יσנלΣ║מσםבΦ┐¢σט╢µץ░5.25∩╝לΦאלσםבΦ┐¢σט╢µץ░91Φ╜¼µםóΣ╕║Σ║לΦ┐¢σט╢µר»∩╝ט1011011∩╝י2πאגΦ╜¼µםóµצ╣µ│ץσלוµכ¼ΘשñΣ║לσןצΣ╜שµ│ץσעלΣ╣רΣ║לσןצµץ┤µ│ץπאג Φ«íτ«קµ£║τí¼Σ╗╢τ│╗τ╗ƒτפ▒Φ┐נτ«קσש¿πאבµמºσט╢σש¿πאבσ¡רσג¿σש¿∩╝טσלוµכ¼RAMσעלROM∩╝יπאבΦ╛ףσוÑΦ«╛σñחσעלΦ╛ףσח║Φ«╛σñח...
5. **µץ░σ¡קΣ┐íσן╖τתהΦí¿τñ║Σ╕מΦ╜¼µםó**∩╝תσלוµכ¼Σ║לΦ┐¢σט╢πאבσו½Φ┐¢σט╢πאבσםבΦ┐¢σט╢σעלσםבσו¡Φ┐¢σט╢Σ╣כΘק┤τתהΦ╜¼µםó∩╝לΣ╗ÑσןךΣ║לΦ┐¢σט╢τתהΦíÑτáבπאבσןםτáבσעלσמƒτáבΦí¿τñ║∩╝לτנזΦºúΦ┐שΣ║¢σ»╣Σ║מσñהτנזµץ░σ¡קΦ«íτ«קσעלΘפשΦ»»µúאµ╡כΦח│σו│ΘחםΦªבπאג 6. **Φהיσז▓µ│óσ╜ó**∩╝תΣ║זΦºúΣ╕ךσםחµק╢Θק┤πאבΣ╕כΘשםµק╢Θק┤πאב...
2. µץ░σט╢Φ╜¼µםóΣ╕מΣ┐íµב»τ╝צτáב∩╝תΦ«▓ΦºúΣ║לΦ┐¢σט╢πאבσו½Φ┐¢σט╢πאבσםבΦ┐¢σט╢σעלσםבσו¡Φ┐¢σט╢Σ╣כΘק┤τתהΦ╜¼µםó∩╝לΣ╗ÑσןךASCIIτáבπאבUnicodeτ╝צτáבσ£¿Φ«íτ«קµ£║Σ╕¡τתהσ║פτפ¿πאג 3. Φ«íτ«קµ£║Φ╜»Σ╗╢∩╝תµמóΦ«¿µףםΣ╜£τ│╗τ╗ƒτתהΣ╜£τפ¿∩╝לσªגWindowsπאבLinuxπאבMac OSτ¡י∩╝לΣ╗Ñσןךσ║פτפ¿Φ╜»Σ╗╢τתהσטזτ▒╗∩╝לσªג...
2. µץ░µם«Φí¿τñ║Σ╕מΦ┐נτ«ק∩╝תΦ«▓ΦºúΣ║לΦ┐¢σט╢πאבσו½Φ┐¢σט╢πאבσםבΦ┐¢σט╢σעלσםבσו¡Φ┐¢σט╢Σ╣כΘק┤τתהΦ╜¼µםó∩╝לΣ╗ÑσןךΣ║לΦ┐¢σט╢µץ░σ£¿Φ«íτ«קµ£║Σ╕¡τתהσ║פτפ¿πאגµ¡ñσñצ∩╝לΦ┐רΣ╝תµ╢יσןךµ╡«τג╣µץ░Φí¿τñ║πאבσ¡קτ¼ªτ╝צτáב∩╝טσªגASCIIσעלUnicode∩╝יΣ╗ÑσןךΣ╜םµףםΣ╜£τתהµªגσ┐╡πאג 3. µףםΣ╜£τ│╗τ╗ƒσƒ║τíא∩╝תΦºúΘחךµףםΣ╜£τ│╗τ╗ƒ...
3. **µץ░µם«Φí¿τñ║Σ╕מΦ┐נτ«ק**∩╝תΣ╗כτ╗םΣ║לΦ┐¢σט╢πאבσו½Φ┐¢σט╢πאבσםבΦ┐¢σט╢σעלσםבσו¡Φ┐¢σט╢Σ╣כΘק┤τתהΦ╜¼µםó∩╝לΣ╗ÑσןךΣ║לΦ┐¢σט╢ΦíÑτáבΦí¿τñ║µ│ץπאבµ╡«τג╣µץ░Φí¿τñ║µ│ץτ¡יπאגΦ┐רΣ╝תΦ«▓Φºúτ«קµ£»Θא╗Φ╛סσםץσוד∩╝טALU∩╝יσªגΣ╜ץµיºΦíלσךáσחןΣ╣רΘשñτ¡יσƒ║µ£¼Φ┐נτ«קπאג 4. **σ¡רσג¿τ│╗τ╗ƒ**∩╝תσלוµכ¼Σ╕╗σ¡ר∩╝טRAM∩╝יσעל...