- 浏览: 21228 次
-

文章分类
最新评论
八大内部排序:
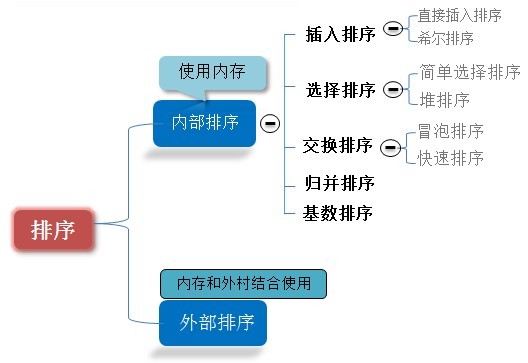
1.直接插入排序:时间复杂度O(n2),空间复杂度O(1),稳定的排序算法
2.希尔排序:时间复杂度O(nlogn),空间复杂度O(1),不稳定的排序算法
3.选择排序:时间复杂度O(n2),空间复杂度O(1),不稳定的排序算法
4.堆排序:时间复杂度O(nlogn),空间复杂度O(1),不稳定的排序算法
5.冒泡排序:时间复杂度O(n2),空间复杂度O(1),稳定的排序算法
6.快速排序:时间复杂度O(nlogn),空间复杂度O(nlogn),不稳定的排序算法
7.归并排序:时间复杂度O(log2n),空间复杂度O(n),稳定的排序算法
8.基数排序:时间复杂度O(d(n+r)),空间复杂度O(n+r),稳定的排序算法
r为基数,d为位数。则基数排序的时间复杂度为O(d(n+r))
八大排序算法比较:

注:直接选择是算法本身是稳定的,只是用顺序存储结构来表现时,会产生不稳定的情况,若用链表来实现,则是稳定的。
八大排序算法合集:

1.直接插入排序:时间复杂度O(n2),空间复杂度O(1),稳定的排序算法
/**
* 直接插入排序
* <ul>
* <li>从第一个元素开始,该元素可以认为已经被排序</li>
* <li>取出下一个元素,在已经排序的元素序列中从后向前扫描</li>
* <li>如果该元素(已排序)大于新元素,将该元素移到下一位置</li>
* <li>重复步骤3,直到找到已排序的元素小于或者等于新元素的位置</li>
* <li>步将新元素插入到该位置中</li>
* <li>重复步骤2</li>
* </ul>
* @param : arr
*/
public static void insertSort(int[] arr){
if(arr==null||arr.length<=1)
return;
int len = arr.length, temp, j;
for(int i=1;i<len;i++){
temp = arr[i];
for(j=i;j>0&&temp<arr[j-1];j--)
arr[j] = arr[j-1];
arr[j] = temp;
}
}
2.希尔排序:时间复杂度O(nlogn),空间复杂度O(1),不稳定的排序算法
/**
* 希尔排序
* @param arr
*/
public static void shellSort(int arr[]) {
if(arr==null||arr.length<=1)
return;
int i, j, gap;
int n = arr.length;
for (gap=n/2; gap>0; gap= gap/2) {
for (i = 0; i<gap; i++) { // 直接插入排序
for (j=i+gap; j<n; j=j+gap){
if (arr[j] < arr[j-gap]) {
int temp = arr[j];
int k = j-gap;
while (k>=0 && arr[k]>temp) {
arr[k+gap] = arr[k];
k = k-gap;
}
arr[k+gap] = temp;
}
}
}
}
}
3.选择排序:时间复杂度O(n2),空间复杂度O(1),不稳定的排序算法
/**
* 选择排序
* <li>在未排序序列中找到最小元素,存放到排序序列的起始位置</li>
* <li>再从剩余未排序元素中继续寻找最小元素,然后放到排序序列末尾。</li>
* <li>以此类推,直到所有元素均排序完毕。</li>
* @param numbers
*/
public static void selectSort(int[] arr){
if(arr==null||arr.length<=1)
return;
int minIndex = 0;
int temp = 0;
for(int i=0; i<arr.length-1;i++){
minIndex = i;
for(int j=i+1;j<arr.length;j++){
if(arr[j]<arr[minIndex])
minIndex = j;
}
if(minIndex!=i){
temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
}
}
4.堆排序:时间复杂度O(nlogn),空间复杂度O(1),不稳定的排序算法
/**
* 堆排序
* @param arr
*/
public static void heapSort(int[] arr) {
if (arr == null || arr.length <= 1)
return;
buildMaxHeap(arr);
for (int i = arr.length - 1; i >= 1; i--) {
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
maxHeap(arr, i, 0);
}
}
private static void buildMaxHeap(int[] arr) {
if (arr == null || arr.length <= 1) {
return;
}
int half = arr.length / 2;
for (int i = half; i >= 0; i--) {
maxHeap(arr, arr.length, i);
}
}
private static void maxHeap(int[] arr, int heapSize, int index) {
int left = index * 2 + 1;
int right = index * 2 + 2;
int largest = index;
if (left < heapSize && arr[left] > arr[index]) {
largest = left;
}
if (right < heapSize && arr[right] > arr[largest]) {
largest = right;
}
if (index != largest) {
int temp = arr[index];
arr[index] = arr[largest];
arr[largest] = temp;
maxHeap(arr, heapSize, largest);
}
}
5.冒泡排序:时间复杂度O(n2),空间复杂度O(1),稳定的排序算法
/**
* 冒泡排序
* <ul>
* <li>比较相邻的元素。如果第一个比第二个大,就交换他们两个。</li>
* <li>对每一对相邻元素做同样工作,从开始第一对到最后一对。最后的元素会是最大数。</li>
* <li>针对所有的元素重复以上的步骤,除了最后一个。</li>
* <li>持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。</li>
* </ul>
* @param : arr
*/
public static void bubbleSort(int[] arr){
if(arr==null||arr.length<=1)
return;
int len = arr.length, temp;
for(int i=1;i<len;i++){
for(int j=0;j<len-i;j++){
if(arr[j]>arr[j+1]){
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
6.快速排序:时间复杂度O(nlogn),空间复杂度O(nlogn),不稳定的排序算法
public static void quickSort(int[] arr) {
if(arr==null||arr.length<=1)
return;
subQuickSort(arr, 0, arr.length - 1);
}
/**
* 快速排序
* <ul>
* <li>从数列中挑出一个元素,称为“基准”</li>
* <li>重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分割之后,
* 该基准是它的最后位置。这个称为分割(partition)操作。</li>
* <li>递归地把小于基准值元素的子数列和大于基准值元素的子数列排序。</li>
* </ul>
* @param arr
* @param start
* @param end
*/
private static void subQuickSort(int[] arr, int start, int end){
if(arr==null||arr.length<=1)
return;
int s = start;
int e = end;
int value = arr[start];
while(s<e){
while(s<e && arr[e]>=value)
e--;
if(s<e){
int temp = arr[s];
arr[s] = arr[e];
arr[e] = temp;
}
while(s<e && arr[s]<=value)
s++;
if(s<e){
int temp = arr[s];
arr[s] = arr[e];
arr[e] = temp;
}
}
if(s>start)
subQuickSort(arr, start, s-1);
if(e<end)
subQuickSort(arr, e+1, end);
}
7.归并排序:时间复杂度O(log2n),空间复杂度O(n),稳定的排序算法
public static void mergeSort(int[] arr) {
if(arr==null||arr.length<=1)
return;
sortArray(arr, 0, arr.length - 1);
}
private static void sortArray(int[] arr, int start, int end) {
// 单个元素不需要排序,直接返回
if (start == end) {
return;
}
int sortSize = end - start + 1;
int seperate;
if (sortSize % 2 == 0) {
seperate = start + sortSize / 2 - 1;
} else {
seperate = start + sortSize / 2;
}
sortArray(arr, start, seperate);
sortArray(arr, seperate + 1, end);
mergeArray(arr, start, seperate, end);
}
private static void mergeArray(int[] arr, int start, int seperate, int end) {
int totalSize = end - start + 1;
int size1 = seperate - start + 1;
int size2 = end - seperate;
int[] array1 = new int[size1];
int[] array2 = new int[size2];
for (int i = 0; i < size1; i++) {
array1[i] = arr[start + i];
}
for (int i = 0; i < size2; i++) {
array2[i] = arr[seperate + 1 + i];
}
int mergeCount = 0;
int index1 = 0;
int index2 = 0;
while (mergeCount < totalSize) {
// 先检查有没有其中的一个数组已经处理完
if (index1 == size1) {
for (int i = index2; i < size2; i++) {
arr[start + mergeCount] = array2[i];
mergeCount++;
index2++;
}
} else if (index2 == size2) {
for (int i = index1; i < size1; i++) {
arr[start + mergeCount] = array1[i];
mergeCount++;
index1++;
}
} else {
int value1 = array1[index1];
int value2 = array2[index2];
if (value1 == value2) {
arr[start + mergeCount] = value1;
arr[start + mergeCount + 1] = value1;
mergeCount += 2;
index1++;
index2++;
} else if (value1 < value2) {
arr[start + mergeCount] = value1;
mergeCount++;
index1++;
} else if (value1 > value2) {
arr[start + mergeCount] = value2;
mergeCount++;
index2++;
}
}
}
}
8.基数排序:时间复杂度O(d(n+r)),空间复杂度O(n+r),稳定的排序算法
r为基数,d为位数。则基数排序的时间复杂度为O(d(n+r))
/**
* 基数排序
* @param arr: 待排列的数组
* @param digit:排列数值中最大值位数
*
*/
public static void radixSort(int[] arr, int digit) {
if(arr==null||arr.length<=1)
return;
final int radix = 10; // 基数
int i = 0, j = 0;
int begin = 0;
int end = arr.length-1;
int[] count = new int[radix]; // 存放各个桶的数据统计个数
int[] bucket = new int[end - begin + 1];
// 按照从低位到高位的顺序执行排序过程
for (int d = 1; d <= digit; d++) {
// 置空各个桶的数据统计
for (i = 0; i < radix; i++) {
count[i] = 0;
}
// 统计各个桶将要装入的数据个数
for (i = begin; i <= end; i++) {
j = getDigit(arr[i], d);
count[j]++;
}
// count[i]表示第i个桶的右边界索引
for (i = 1; i < radix; i++) {
count[i] = count[i] + count[i - 1];
}
// 将数据依次装入桶中
// 这里要从右向左扫描,保证排序稳定性
for (i = end; i >= begin; i--) {
j = getDigit(arr[i], d); // 求出关键码的第k位的数字, 例如:576的第3位是5
bucket[count[j] - 1] = arr[i]; // 放入对应的桶中,count[j]-1是第j个桶的右边界索引
count[j]--; // 对应桶的装入数据索引减一
}
// 将已分配好的桶中数据再倒出来,此时已是对应当前位数有序的表
for (i = begin, j = 0; i <= end; i++, j++) {
arr[i] = bucket[j];
}
}
}
// 获取x这个数的d位数上的数字
// 比如获取123的1位数,结果返回3
private static int getDigit(int x, int d) {
return ((x / (int)Math.pow(10, d)) % 10);
}
八大排序算法比较:

注:直接选择是算法本身是稳定的,只是用顺序存储结构来表现时,会产生不稳定的情况,若用链表来实现,则是稳定的。
八大排序算法合集:
public class Sort {
/**
* 直接插入排序
* <ul>
* <li>从第一个元素开始,该元素可以认为已经被排序</li>
* <li>取出下一个元素,在已经排序的元素序列中从后向前扫描</li>
* <li>如果该元素(已排序)大于新元素,将该元素移到下一位置</li>
* <li>重复步骤3,直到找到已排序的元素小于或者等于新元素的位置</li>
* <li>步将新元素插入到该位置中</li>
* <li>重复步骤2</li>
* </ul>
* @param : arr
*/
public static void insertSort(int[] arr){
if(arr==null||arr.length<=1)
return;
int len = arr.length, temp, j;
for(int i=1;i<len;i++){
temp = arr[i];
for(j=i;j>0&&temp<arr[j-1];j--)
arr[j] = arr[j-1];
arr[j] = temp;
}
}
/**
* 希尔排序
* @param arr
*/
public static void shellSort(int arr[]) {
if(arr==null||arr.length<=1)
return;
int i, j, gap;
int n = arr.length;
for (gap=n/2; gap>0; gap= gap/2) {
for (i = 0; i<gap; i++) { // 直接插入排序
for (j=i+gap; j<n; j=j+gap){
if (arr[j] < arr[j-gap]) {
int temp = arr[j];
int k = j-gap;
while (k>=0 && arr[k]>temp) {
arr[k+gap] = arr[k];
k = k-gap;
}
arr[k+gap] = temp;
}
}
}
}
}
/**
* 选择排序
* <li>在未排序序列中找到最小元素,存放到排序序列的起始位置</li>
* <li>再从剩余未排序元素中继续寻找最小元素,然后放到排序序列末尾。</li>
* <li>以此类推,直到所有元素均排序完毕。</li>
* @param numbers
*/
public static void selectSort(int[] arr){
if(arr==null||arr.length<=1)
return;
int minIndex = 0;
int temp = 0;
for(int i=0; i<arr.length-1;i++){
minIndex = i;
for(int j=i+1;j<arr.length;j++){
if(arr[j]<arr[minIndex])
minIndex = j;
}
if(minIndex!=i){
temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
}
}
/**
* 堆排序
* @param arr
*/
public static void heapSort(int[] arr) {
if (arr == null || arr.length <= 1) {
return;
}
buildMaxHeap(arr);
for (int i = arr.length - 1; i >= 1; i--) {
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
maxHeap(arr, i, 0);
}
}
private static void buildMaxHeap(int[] arr) {
if (arr == null || arr.length <= 1) {
return;
}
int half = arr.length / 2;
for (int i = half; i >= 0; i--) {
maxHeap(arr, arr.length, i);
}
}
private static void maxHeap(int[] arr, int heapSize, int index) {
int left = index * 2 + 1;
int right = index * 2 + 2;
int largest = index;
if (left < heapSize && arr[left] > arr[index]) {
largest = left;
}
if (right < heapSize && arr[right] > arr[largest]) {
largest = right;
}
if (index != largest) {
int temp = arr[index];
arr[index] = arr[largest];
arr[largest] = temp;
maxHeap(arr, heapSize, largest);
}
}
/**
* 冒泡排序
* <ul>
* <li>比较相邻的元素。如果第一个比第二个大,就交换他们两个。</li>
* <li>对每一对相邻元素做同样工作,从开始第一对到最后一对。最后的元素会是最大数。</li>
* <li>针对所有的元素重复以上的步骤,除了最后一个。</li>
* <li>持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。</li>
* </ul>
* @param : arr
*/
public static void bubbleSort(int[] arr){
if(arr==null||arr.length<=1)
return;
int len = arr.length, temp;
for(int i=1;i<len;i++){
for(int j=0;j<len-i;j++){
if(arr[j]>arr[j+1]){
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
public static void quickSort(int[] arr) {
if(arr==null||arr.length<=1)
return;
subQuickSort(arr, 0, arr.length - 1);
}
/**
* 快速排序
* <ul>
* <li>从数列中挑出一个元素,称为“基准”</li>
* <li>重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分割之后,
* 该基准是它的最后位置。这个称为分割(partition)操作。</li>
* <li>递归地把小于基准值元素的子数列和大于基准值元素的子数列排序。</li>
* </ul>
* @param arr
* @param start
* @param end
*/
private static void subQuickSort(int[] arr, int start, int end){
if(arr==null||arr.length<=1)
return;
int s = start;
int e = end;
int value = arr[start];
while(s<e){
while(s<e && arr[e]>=value)
e--;
if(s<e){
int temp = arr[s];
arr[s] = arr[e];
arr[e] = temp;
}
while(s<e && arr[s]<=value)
s++;
if(s<e){
int temp = arr[s];
arr[s] = arr[e];
arr[e] = temp;
}
}
if(s>start)
subQuickSort(arr, start, s-1);
if(e<end)
subQuickSort(arr, e+1, end);
}
public static void mergeSort(int[] arr) {
if(arr==null||arr.length<=1)
return;
sortArray(arr, 0, arr.length - 1);
}
private static void sortArray(int[] arr, int start, int end) {
// 单个元素不需要排序,直接返回
if (start == end) {
return;
}
int sortSize = end - start + 1;
int seperate;
if (sortSize % 2 == 0) {
seperate = start + sortSize / 2 - 1;
} else {
seperate = start + sortSize / 2;
}
sortArray(arr, start, seperate);
sortArray(arr, seperate + 1, end);
mergeArray(arr, start, seperate, end);
}
private static void mergeArray(int[] arr, int start, int seperate, int end) {
int totalSize = end - start + 1;
int size1 = seperate - start + 1;
int size2 = end - seperate;
int[] array1 = new int[size1];
int[] array2 = new int[size2];
for (int i = 0; i < size1; i++) {
array1[i] = arr[start + i];
}
for (int i = 0; i < size2; i++) {
array2[i] = arr[seperate + 1 + i];
}
int mergeCount = 0;
int index1 = 0;
int index2 = 0;
while (mergeCount < totalSize) {
// 先检查有没有其中的一个数组已经处理完
if (index1 == size1) {
for (int i = index2; i < size2; i++) {
arr[start + mergeCount] = array2[i];
mergeCount++;
index2++;
}
} else if (index2 == size2) {
for (int i = index1; i < size1; i++) {
arr[start + mergeCount] = array1[i];
mergeCount++;
index1++;
}
} else {
int value1 = array1[index1];
int value2 = array2[index2];
if (value1 == value2) {
arr[start + mergeCount] = value1;
arr[start + mergeCount + 1] = value1;
mergeCount += 2;
index1++;
index2++;
} else if (value1 < value2) {
arr[start + mergeCount] = value1;
mergeCount++;
index1++;
} else if (value1 > value2) {
arr[start + mergeCount] = value2;
mergeCount++;
index2++;
}
}
}
}
/**
* 基数排序
* @param arr: 待排列的数组
* @param digit:排列数值中最大值位数
*
*/
public static void radixSort(int[] arr, int digit) {
if(arr==null||arr.length<=1)
return;
final int radix = 10; // 基数
int i = 0, j = 0;
int begin = 0;
int end = arr.length-1;
int[] count = new int[radix]; // 存放各个桶的数据统计个数
int[] bucket = new int[end - begin + 1];
// 按照从低位到高位的顺序执行排序过程
for (int d = 1; d <= digit; d++) {
// 置空各个桶的数据统计
for (i = 0; i < radix; i++) {
count[i] = 0;
}
// 统计各个桶将要装入的数据个数
for (i = begin; i <= end; i++) {
j = getDigit(arr[i], d);
count[j]++;
}
// count[i]表示第i个桶的右边界索引
for (i = 1; i < radix; i++) {
count[i] = count[i] + count[i - 1];
}
// 将数据依次装入桶中
// 这里要从右向左扫描,保证排序稳定性
for (i = end; i >= begin; i--) {
j = getDigit(arr[i], d); // 求出关键码的第k位的数字, 例如:576的第3位是5
bucket[count[j] - 1] = arr[i]; // 放入对应的桶中,count[j]-1是第j个桶的右边界索引
count[j]--; // 对应桶的装入数据索引减一
}
// 将已分配好的桶中数据再倒出来,此时已是对应当前位数有序的表
for (i = begin, j = 0; i <= end; i++, j++) {
arr[i] = bucket[j];
}
}
}
// 获取x这个数的d位数上的数字
// 比如获取123的1位数,结果返回3
private static int getDigit(int x, int d) {
return ((x / (int)Math.pow(10, d)) % 10);
}
// 打印完整序列
public static void printArr(int[] arr) {
for (int value : arr) {
System.out.print(value + "\t");
}
System.out.println();
}
public static void main(String[] args) {
int[] arr = { 50, 123, 543, 187, 49, 30, 0, 2, 11, 100,2000,3002,1001};
System.out.print("排序前:\t");
printArr(arr);
insertSort(arr);
shellSort(arr);
selectSort(arr);
heapSort(arr);
bubbleSort(arr);
quickSort(arr);
mergeSort(arr);
radixSort(arr,4);
System.out.print("排序后:\t");
printArr(arr);
}
}
发表评论
-
Java中的format相关知识小结
2016-04-29 00:33 5691.Java中format相关的类结构: 2. ... -
Java中String类总结
2016-04-18 22:48 637Java中String类总结 1.String类继承了Seri ... -
常用查找算法的Java实现
2016-04-20 21:26 153151.顺序查找 /**顺序查找平均时间复杂度 O(n) * ... -
Java数组使用注意事项
2016-04-16 19:21 10331.数组必须使用new分配内存空间后才可使用,并进行默认的初始 ... -
Java中不引入第三个变量实现两个变量值的交换
2016-04-16 18:09 985int a,b; a=5;b=10; ... -
Java基本数据类型
2016-04-16 17:26 568数据类型内存空间取值� ... -
Java标识符
2016-04-16 13:45 8141.java中的标识符有字母、数字、下划线、美元符号组成。 2 ... -
Java环境变量配置
2016-04-16 12:30 698Windows操作系统下: 我的电脑-属性-高级-环境变量-系 ...






相关推荐
这里我们主要关注Java实现的七大经典排序算法:冒泡排序、插入排序、选择排序、希尔排序、快速排序、归并排序以及堆排序。 1. 冒泡排序(Bubble Sort): 冒泡排序是最简单的排序方法之一,它通过重复遍历待排序的...
本文将深入探讨标题"常用排序算法java演示"中涉及的知识点,包括排序算法的原理、Java实现方式以及其在实际应用中的图形演示。 首先,让我们逐一了解几种常见的排序算法: 1. **冒泡排序(Bubble Sort)**:这是一...
本篇文章将详细讲解标题中提到的六种常见排序算法的Java实现。 1. **冒泡排序**:冒泡排序是最基础的排序算法之一,它通过不断交换相邻的逆序元素来逐渐将较大的元素“浮”到数组的前端。在Java中,冒泡排序的基本...
本资源"常用各种排序算法Java的实现_差不多了__.rar"显然是一个包含了各种经典排序算法Java实现的压缩文件,对于学习和理解这些算法的开发者来说极具价值。 首先,我们来概述一下常见的排序算法: 1. 冒泡排序:是...
### 十大常用排序算法(Java实现) #### 冒泡排序 **定义与原理:** 冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地...
以上就是Java中实现的一些常用排序算法,它们各有优缺点,适用于不同的场景。理解并熟练掌握这些排序算法,有助于优化代码性能,提高编程能力。在实际开发中,应根据具体需求选择合适的排序算法,以达到最佳的效率和...
这里我们主要关注Java实现的排序算法,并结合一个PPT的动画演示来探讨其中的插入排序、直接插入排序和希尔排序。 首先,让我们深入理解插入排序。插入排序是一种简单的排序算法,其基本思想是将未排序的元素逐个...
虽然树形选择排序和堆排序在这次实现中未涵盖,但理解这四种排序算法的基本原理和Java实现方式对于提升编程技能至关重要。 首先,让我们来看看插入排序。插入排序是一种简单直观的排序算法,它的工作原理类似于人们...
### 常用排序算法分析与实现(Java版) #### 插入排序 **1. 直接插入排序** 直接插入排序是一种简单的排序方法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并...
这个名为"常用排序算法JAVA版"的压缩包文件很可能包含了Java实现的各种经典排序算法,如冒泡排序、选择排序、插入排序、快速排序、归并排序、堆排序等。 1. **冒泡排序**:是最简单的排序算法之一,通过不断交换...
以上就是六种常用的内部排序算法在Java语言中的实现。理解这些排序算法的原理和性能特点,有助于在实际编程中选择合适的排序方法,提高程序效率。对于面试或者笔试,熟练掌握这些算法将大大提高你的竞争力。在实践中...
冒泡排序和快速排序是两种基础但广泛使用的数据排序算法。冒泡排序由于其简单直观的特性,易于理解和实现,而快速排序则以其较高的效率在数据量较大时展现出优势。 首先,让我们来看冒泡排序算法。冒泡排序通过重复...
常用排序算法的Java实现源码,包括冒泡排序,快速排序,直接插入排序,希尔排序,直接选择排序,堆排序,归并排序,基数排序,计数排序。
在计算机科学中,排序算法是数据处理的重要组成部分,它们用于将一组无序的数据按照特定顺序进行排列。这里我们将深入探讨八大排序算法,并结合Java语言来理解它们的实现原理。 1. 冒泡排序(Bubble Sort) 冒泡...
在编程领域,排序算法是计算机科学中的核心概念,特别是在Java这样的高级编程语言中。排序算法是用来组织和优化数据结构的关键工具,使得数据按照特定规则(如升序或降序)排列。以下是对Java中几种常见排序算法的...
本资源提供了五种经典的排序算法的Java实现,包括选择排序(Selection Sort)、插入排序(Insertion Sort)、希尔排序(Shell Sort)、归并排序(Merge Sort)以及快速排序(Quick Sort)。 1. **选择排序**:选择排序是一种...
学习资料如"Java常用排序算法程序员必须掌握的8大排序算法Java开发Java经验技巧共16页.pdf"可以提供详细的讲解和示例,帮助你更好地理解和实践这些算法。同时,这些排序算法不仅限于Java,也广泛应用于Python、C语言...
### Java常用八大排序算法详解 #### 一、直接插入排序 **基本思想:** 直接插入排序的基本思路是在要排序的一组数中,假设前面 (n-1) [n>=2] 个数已经排好顺序,现在要把第 n 个数插入到前面的有序数列中,使得这 ...
这篇博客“常用排序算法小结(附Java实现)”提供了一种深入理解并掌握常见排序算法的途径,尤其对于Java开发者来说非常实用。文章可能涵盖了如冒泡排序、选择排序、插入排序、快速排序、归并排序、堆排序等多种经典...
本资料包聚焦于"Java常用排序算法"和"程序员必须掌握的8大排序算法",并深入探讨了"二分法查找"这一高效搜索技术。 首先,我们来看八大排序算法。这些算法包括: 1. **冒泡排序**:最简单的排序方法,通过不断交换...