CAP定理（CAP theorem）

在计算机科学中, CAP定理（CAP theorem）, 又被称作 布鲁尔定理（Brewer's theorem）, 它指出对于一个分布式计算系统来说，不可能同时满足以下三点:

• 一致性(Consistency) (所有节点在同一时间具有相同的数据)
• 可用性(Availability) (保证每个请求不管成功或者失败都有响应)
• 分隔容忍(Partition tolerance) (系统中任意信息的丢失或失败不会影响系统的继续运作)

CAP理论的核心是：一个分布式系统不可能同时很好的满足一致性，可用性和分区容错性这三个需求，最多只能同时较好的满足两个。

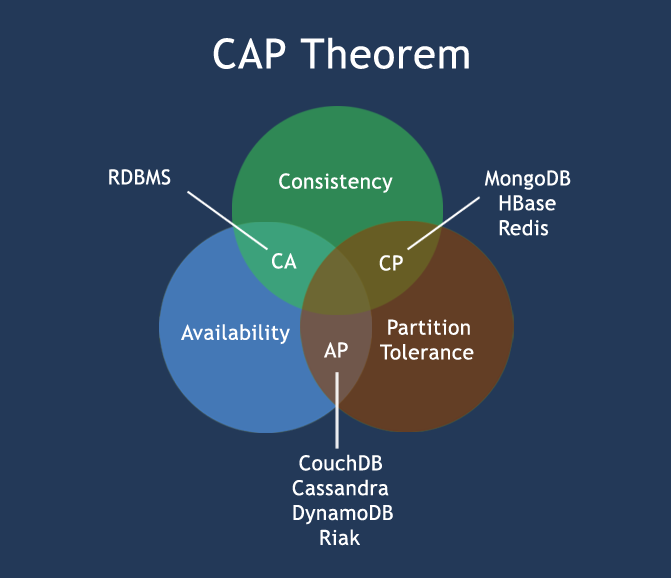
因此，根据 CAP 原理将 NoSQL 数据库分成了满足 CA 原则、满足 CP 原则和满足 AP 原则三 大类：

• CA - 单点集群，满足一致性，可用性的系统，通常在可扩展性上不太强大。
• CP - 满足一致性，分区容忍必的系统，通常性能不是特别高。
• AP - 满足可用性，分区容忍性的系统，通常可能对一致性要求低一些。