http://blog.csdn.net/pi9nc/article/details/11401625
原文地址:Toward More Realistic Pathfinding by Marco Pinter
A Faster Implementation of the Standard A*
作者实现的快速A*算法是使用一个虚拟的matrix嵌套在地图方格上,matrix为固定大小60*60,matrix和地图方格对齐方式为:matrix的正中心点(30,30)与起点终点的正中间点M重叠,示意图见下:
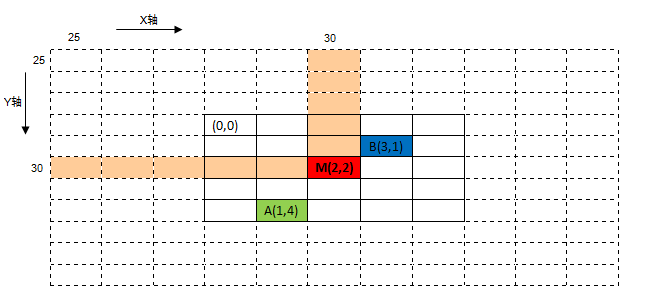
示意图中的实线方格为地图坐标体系,虚线方格为matrix的坐标,A点为起点,B点为终点,M点为AB的中间点。下面演算一下这两个坐标体系间的变换,非常简单,公式中的A.x表示地图坐标体系中的X轴坐标值,A.x'表示matrix中的值。
M点在地图中为(2,2),在matrix中为(30,30),即:M.x=2, M.y=2, M.x'=30, M.y' = 30。A点在matrix中的坐标值计算方法:
A.x' = A.x + (30 - M.x) = 1 + (30 - 2) = 29
A.y' = A.y + (30 - M.y) = 4 + (30 - 2) = 32
B点为:
B.x' = B.x + (30 - M.x) = 3 + (30 - 2) = 31
B.y' = B.y + (30 - M.y) = 1 + (30 - 2) = 29
Smoothing the A* Path
路径平滑处理算法是在寻路算法完成后执行的,该算法使用一个 Walkable(pointA, pointB) 函数检测路径上的两个 waypoint 是否可直接到达,如果是则取消两点中间的 waypoint,具体算法为:
A = 起点
B = 路径上的第一个 waypoint,即起点A的下一个 waypoint
while (B->next != NULL)
if Walkable(A, B->next)
// 可通行,移除B,B点后移
temp = B
B = B->next
delete temp from the path
else
// 不可通行,将两点后移
A = B
B = B->next
Walkable(pointA, pointB) 函数检测路径是否可通行的方法为:将物体沿路径每次移动一个单位(比如:0.1个单元格),然后检测物体的中心点以及4个顶点(物体被视为正方形,4个顶点的坐标由中心点坐标和物体宽度决定)所在的单元格是否为障碍物,只要有一个是则返回false,如果整个路径都没有碰到障碍物则返回true,参见原文中的 FIGURE 3。
这个简单平滑处理算法类似于“line of sight(视线机制)”,中间路径点被逐个跳过一直到最后一个能从当前位置看到的点。该算法虽然简单,但很真实、准确,因为它提供了基于物体的宽度进行障碍物检测的机制,同时也很容易和后面介绍的 the realistic turning methods 结合。
Legal Turns: The Directional A* Algorithm
带方向的A*算法在节点的XY轴基础上增加了一个第3维度“方向(orientation)”,其取值为8个基本的地理指向:N, S, E, W, NE, NW, SE, SW,比如,某个节点可表示为:[X = 92, Y = 142, orientation = NW]。节点数量也因此扩大8倍,从一个节点到达另一个节点的可能路径数变为原来的64倍,因为在起点可以有8个不同的方向,到达终点时也可以是这8个方向中的任意一个。
Directional A*算法的计算过程不再只是简单地查看子节点q是否可通过就行了,还得计算是否存在一条从父节点p到子节点q的曲线(curved path)存在,需要将物体在p、q点的方向以及转弯半径(turning radius)考虑在内;如果存在这样一条曲线路径还得移动过程中检查是否会碰上障碍物。只有所有这些条件都满足的情况下才认为子节点是有效的。給定物体的大小和转弯半径,就可以使用这个算法得到一个完整的有效路径。
Directional Curved Paths
给定物体的起点和终点以及物体在起点和终点的方向,从起点到终点可以有4条不同的路径(参见原文图9)。这些路径都是由3段线路构成:起点所在圆的弧线、中间直线、终点所在圆的弧线。
计算这些路径的关键在于获得物体离开起点圆的点Q1和进入终点圆的点Q2的坐标和方向,即为求解中间直线与两圆的切点。存在两种情况:一种是物体在两个圆上的转动方向相同,另一种是转动方向不同。具体算法原文中有详细描述。
The modified heuristic
Directional A* 算法需要新的 heuristic 值计算方法,需要将中间点的方向考虑在内,朝向目标点的中间点更佳,同时也必须将转弯半径考虑进去。显而易见,heuristic 的值就是从中间点以当前速度方向到达目标点的最短弧线距离,具体方法见“Adding Realistic Turns”部分。
如果在寻路过程中为每个中间点算一次 heuristic 值,那么将是一笔不小的系统开销;通过建立一个 heuristic table 就免除这个动态计算开销。heuristic table 存放以“任意角度”到达距当前点10个单元格距离内“任意点”的弧线路径长度值。需要注意的是,“任意角度”和“任意点”都不是“任意”的,“任意角度”指的是[0, pi)范围内单位大小为 pi/8 的8个角度(速度方向与当前点到目标点方向间的夹角值范围为[0, pi]);“任意点”指的是精度为 1/64 单元格的地图坐标上的关键点,10个单元格内一共有 640 个这样的点。
计算时只需要将中间点的方向和到目标点的距离近似到 heuristic table 上就可以查询到中间点的 heuristic 值,因为 heuristic 值本身的意义就是一个到目标点的 cost 估计值,因此不要求十分精确。
因为 heuristic table 中存放的是弧线路径长度,所以如果转弯半径发生变化,heuristic table 就需要重新生成。
Using a hit-check table
获得物体从起点移动到终点的最短路径后(即上面的 curved path),我们需要知道物体沿该路径移动会和那些单元格发生“hit”接触。为了避免重复计算,可以建立一个 hit-check table来记录物体沿路径移动会 hit 的单元格。
物体在起点和终点可以有8个方向,在 Directional-48 算法中共有48个目标点,因此共有 8*8*48 = 3072 条最短路径,需要为这3027条路径都分别建立 hit-check table。
为单条路径建立 hit-check table 的方法为:将物体沿路径每次移动一个单位长度,然后标记物体中心点和4个顶点所在单元格为 hit 状态(见下图)。需要注意的是,hit-check table 是绑定物体的大小和转弯半径的,也就是说如果这两个参数开发变化 hit-check table 就需要重新计算!
此外,hit-check table 计算是基于物体的起点位于单元格的中心位置的前提,然而实际情况却不一定符合该前提;如果起点不在单元格中心位置并且我们需要检查起点与周围邻接点的 hit 状态,那么就需要动态地检查路径是否可行,而不能基于 hit-check table,因为在这种情况下 hit-check table 可能是不正确的。

Fixed-Angle Character Art
Directional A* 算法的计算过程都是假设物体可以沿任意角度进行移动,而不是固定的8个或者16个方向;大多数非3D的游戏都属于后者,因此就需要对路径进行修正,幸运的是路径修正并不十分复杂。
圆弧的修正算法:
1. 首先,可以想象为在圆外绘制了一个外切的等角八边行(之所以是八边形是和算法中了物体只能沿8个基本方向移动相对照的,很容易扩展到16个),八边形的每一个边对应2个直角三角形(见原文图示15),每个直角三角形位于圆内的锐角为 pi/8,其对应的直角边长度为 r * tan(pi/8);
2. 将弧线的起点和终点从圆周上延伸到上述八边形上,然后重新计算两点在八边形上的距离;
直线的修正算法:
1. 首先,若线段斜度为 pi/8 的整数倍(或为“无限”接近整数倍),则不用进行修正;
2. 对于非标准角度的线段,使用2条标准角度的直线与原线段构成的折线来替代原线段(见原文图示15),要求是与原线段最接近的2条标准角度的直线;
直线修正算法涉及到小学几何学知识,此处稍微温故一下:
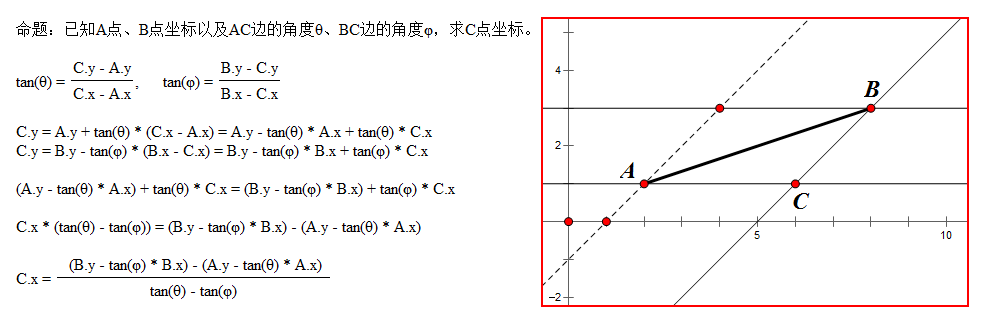
圆弧路径使用原来的"line segment"保存修正后的路径信息,实际就是更新了一下路径的长度,物体在路径移动的详细位置信息可以在实际移动过程中动态计算获得。直线路径修正后则扩展成了2条相接的线段,所以从起点A移动到终点B最多需要4个"line segment"来保存构成路径的线段。
A Better Smoothing Pass
Smoothing-48 算法可以为使用普通 Non-Directional A* Search 算法获得的路径进行平滑优化,使得路径到达 Directional-48 生成的弧线路径效果。Smoothing-48 算法实际是一个快速版的 Directional-48,区别在于 Smoothing-48 是沿着已生成的路径进行处理,它只对路径上 waypoint 之间的路径进行处理,通常是 waypoint 和它前面2、3个单元格距离的 waypoint 之间的路径,因此 Smoothing-48 并不会产生新的 waypoint。
Smoothing-48 算法对 heuristic 值的计算方法进行了调整,倾向于能够保持原有路径方向的路径,该算法会尝试每个 waypoint 的各个方向,以及所有2、3个单元格距离的 waypoint 之间的路径,从而找到一条最佳路径。
混合使用 Non-Directional A* Search 和 Smoothing-48 算法既可以到达 Directional-48 的路径效果,也可以大大降低计算量,Performance and Hybrid Solutions 章节提供了具体的实现方法。
如果原始路径中有 illegal turn,并且沿着原始路径不存在 legal ways 来完成转弯,那么 Smoothing-48 算法也只能失败,因为 Smoothing-48 并不能产生一条完全不同的路径,此时只能使用 Directional Search 或者 Hybrid Method 来找到有效的弧线路径。
Path Failure and Timeslicing
A * 以及其派生寻路算法的最大缺陷在于如果路径寻找失败那么将造成极糟的计算消耗,为了减轻这个问题必须要把失败的可能降到最低。可以通过把地图划分成小的区域,并提前计算好任意两个区域之间的通行状况,只需要一个 bit 位就可记录两个区域间的通行情况。在开始执行寻路前先检查该区域通行表,如果两个区域之间无法通行则立即出错返回,反之则正常执行寻路。
寻路过程中的 timeslicing 问题是指当执行一个很慢的寻路计算时,其它物体的寻路请求就会被挂起直到该慢寻路计算完。为了降低慢寻路对性能的影响,可以创建两个 matrices,其中一个用来处理较少发生的慢寻路计算,另一个则负责处理快速寻路请求,即为多线程模式。
Performance and Hybrid Solutions
混合寻路算法:
1. 先使用 Non-Directional-4 进行简单寻路,如果失败则结束;
2. 使用 Smoothing-48 算法对路径进行处理,如果成功则跳到第6步,否则找到最远能达到的路径点 ia,接着做第3步;
3. 再次使用 Smoothing-48 算法从终点往起点方向回溯,找到能到达的最远路径点 ib;
4. 路径点 ia 和 ib 之间是需要重新寻找路径的部分,如果两点在X轴或者Y轴的坐标距离超过12个单元格,则失败返回,
否则从 ia 和 ib 点背向后移直到两点的坐标距离在水平或者垂直方向上超过12个单元格;
5. 在上面的 ia 和 ib 之间执行 Direction-8 寻路,如果失败则结束,成功则将3段路径连接起来构成新路径;
6. 最后对找到的路径执行基本的 Smoothing 处理;
混合寻路算法的优点在于提供高效的寻路机制,避免寻路失败产生的高计算开销,同时使用 Smoothing-48 算法可以保证路径平滑和有效。
Speed and Other Movement Restrictions
速度对路径选择的影响是一个比较复杂的问题,如原文图22中所示,寻路算法找到的绿线表示的距离最短的路径(有很多弯道),但对用加速、减速较满的物体来说,图中的蓝线路径才是最快的,因为它只需要转2次弯,而且大部分路径线段都是可以高速移动的直线。
解决这个问题的一个简单方法就是将速度作为一个因素加入到 cost 计算公式中,并加大转弯的 cost 值,这将 penalize turning,因为转弯是需要减速的(该问题产生的前提)。不过这个方法只对 Directional-24 和 Directional-48 有效,并不适用于 Directional-8,因为后者会产生太多的弯道从而影响准确性。
People Movement and Friendly-Collision Avoidance
Fluid turning radius
目前讲到的 Directional Search 算法都是基于固定转弯半径和物体大小的,而现实中的情况是物体的转弯半径通常是由其速度决定的,是一个动态值,尤其是对于“人物”对象,很容易减速然后转个小弯。
在转弯半径可变的情况下寻路是异常复杂的,需要更多的内存来存放一定范围内转弯半径对应的中间数据表,同时在正式的寻路算法中还需要增加新的维度来追踪速度,并且计算弯道路径和过弯速度时需要将加速度大小考虑进去。
下面提供了2个简单的解决办法:
1. 先执行 standard A* search,然后在转弯前物体适当减速;
2. 设置一个很小的转弯半径,然后执行 Directional search,加大对转弯的“惩罚”,这样有利于不需要过多小弯的路径;
Friendly-collision avoidance
对于物体间需要保持“友好”状态的游戏,需要一些措施来避免物体发生碰撞,并继续朝目标行进。一个有效的方法是:每隔大约半秒计算一次每个物体沿当前路径在2秒后移动到的地图单元格,然后检查哪些物体可能会发生碰撞。如果预期发生碰撞,那么物体应立即开始减速,并找一条能够绕开会发生碰撞单元格的新路线。一旦路径不再发生交叉,物体就可以重新加速。
理想情况下,物体应该总是选择右手边来绕行,从而避免物体面对面时发生“绕行冲突”的情况(就和我们现实中的情况一样)。尽管如此,物体任然可能由于相距太近而发生碰撞,这时候物体应该足够聪明能停下来,朝右手边绕行,如果没有足够的空间可通过则先后退一步,等等。
程序代码分析
源程序中的函数 SetupDirOffsets() 为Directional-48 算法中的48个邻接节点建立了相对于当前位置的坐标偏移索引表,48个邻接节点的顺序见下图:
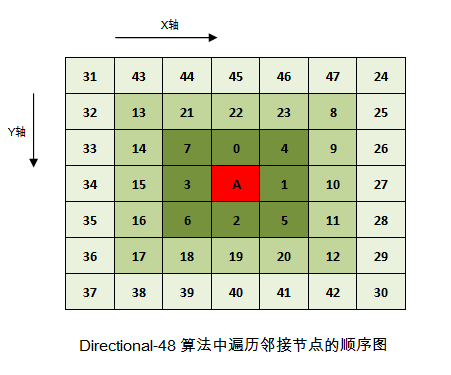
基于这个坐标偏移索引表就可以轻松得到任何一个邻接节点的坐标位置,比如第17邻接点相对于A点的坐标偏移值为:[-2, 2],那么其坐标值为:[A.x - 2, A.y + 2]








相关推荐
Mitigate the risks involved in migrating away from a proprietary database platform toward MariaDB’s open source database engine. This book will help you assess the risks and the work involved, and ...
Moore是NetFPGA SUME的主要发起人和作者,他们分别来自剑桥大学和斯坦福大学,并在IEEE Micro上发表了一篇题为“NetFPGA SUME: Toward 100 Gbps as Research Commodity”的经典论文,详细介绍了这一项目。...
《TGIF-QA: Toward Spatio-Temporal Reasoning in Visual Question Answering》这篇论文则是深入探讨了VQA在视频领域的拓展,并提供了在时空推理上的三重重要贡献。 首先,论文提出了三个针对视频VQA的新任务,这些...
Indium gallium nitride (InGaN)-based light-emitting diodes (LEDs) are considered a promising candidate for red-green-blue (RGB) micro displays. Currently, the blue and green LEDs are efficient, while ...
智能制造转型是当前工业发展的重要方向,它依托于人工智能、工业互联网等先进技术,将传统的制造系统升级为能够自主学习和适应的智能系统。新一代智能制造,意味着制造过程中的数据获取、处理、分析和应用将更加智能...
- **高效性**:SweetDroid的设计考虑到了存储和计算开销的问题,通过优化算法和数据结构,使得系统在执行过程中引入的额外开销较小。 #### 实验验证 为了验证SweetDroid的有效性和实用性,研究团队在其上千个...
一氧化氮对铝胁迫下不同小麦基因型根系AsA-GSH循环的影响,孙成亮,刘立娟,以2个小麦基因型鉴-864(耐性)和扬麦-5号(敏感)为材料,在水培条件下研究了铝胁迫下一氧化氮(NO)对抗坏血酸(AsA)-谷胱甘肽(GSH)循�
Structured ultrashort-pulse laser beams, and in particular eigenmodes of the paraxial Helmholtz equation, are currently extensively studied for novel potential applications in various fields, e.g., ...
奈达代表作书名Toward a Science of Translating译成"翻译科学探索"引起译论界高度的关注和激烈争论。译文"翻译科学探索"中的两个词——"翻译科学"和"探索",都值得很好的商榷。Toward a Science of Translating的...
Although semantic-based composition approaches have brought some comprehensive advantages such as higher precisions and recalls, they are far from the real practice and hard to be applied in real-...
The discriminant validity of the stroop color and word test: Toward a cost-effective strategy to distinguish subgroups of disruptive preadolescents PsycholoEy in the Schools Volume 31. April 1994 ...
思科CCNA学习笔记 思科CCNA学习笔记是网络工程师的必备知识,涵盖了计算机网络的基本概念、OSI与TCP/IP协议框架、IP报文传输过程、传输层功能、TCP与UDP对比等内容。以下是该笔记的详细知识点: 一、OSI与TCP/IP...
The life of the self: Toward a new psychology. New York: Basic Books, 190 pp., [dollar]6.95 414 Book Reviews the importance of having a thorough knowledge of various assessment instruments, a ...
As the flat panel displays (Liquid Crystal Displays, AMOLED, etc.) reach near perfection in their viewing qualities and display areas, it is natural to seek the next level of displays, including 3D ...
Oracle Database 10g Release 2是Oracle公司在2004年至2005年间备受赞誉的一款数据库管理系统,获得了多项业界大奖,包括eWeek分析师选择奖、2004年I.E.读者首选最佳数据库管理系统、CRN五星级推荐、DM Review 2005...
### Mean Shift: A Robust Approach Toward Feature Space Analysis #### 概述 本文由Dorin Comaniciu和Peter Meer撰写,发表于2002年5月的《IEEE Transactions on Pattern Analysis and Machine Intelligence》...
We report a quantum key distribution (QKD) system that uses light-emitting-diodes (LEDs) at 1310 nm as optical sources. Compared to the normally used laser diodes (LDs), LEDs are easier to manufacture...
在重排序算法下抽取重要度高的RDF语句形成摘要,用户可以设定摘要长度。通过建立本体摘要原型系统进行实验,实验结果表明,该摘要方法能够为用户提供满足其偏好的最优摘要本体,利于用户理解本体,不但方便了语义...
等几何分析(Isogeometric Analysis)是一种有限元分析的新方法,这一概念最早在2005年由T.J.R. Hughes等人提出。该方法利用非均匀有理B样条(NURBS)作为基础函数,构建精确的几何模型,并在分析中进行细化和/或...