首先,先复习一下二叉树的一些基本知识
树:是一种非线性数据结构。
二叉树:是每个结点最多有两个子树的有序树
根节点:最上面的节点
叶节点:没有子树的节点
深度:二叉树的层数,就是高度。
 右图就是一个二叉树,A为根节点,D、E、F为叶节点,深度为2
右图就是一个二叉树,A为根节点,D、E、F为叶节点,深度为2
那么什么是哈弗曼树呢?
哈夫曼树是最优二叉树,何为最优二叉树?就是每个叶节点到根节点的路径都是唯一且最短的。节点的权值越大则离根节点越远。其中,权值一般是该节点内容出现的频率。
大家可能会有疑问,为什么哈弗曼树是最优的呢?为什么可以起到压缩文件的作用呢?
我们学过的线性数据结构有数组、链表和栈,当数据以这种数据结构存储的时候,我们搜索数据就要依次遍历直至找到该数据。而哈夫曼树就简化了遍历的过程,我们在建哈夫曼树的规则是:
1.将数组数据从小到大排序。
2.生成一个新的节点,该节点的权值是最小的节点的权值和,该节点是最小两个节点的父节点。
3.在数组数据中除去最小的两个节点,加上新的节点。
4.排序
5.依次循环,只剩一个节点,该节点则为根节点。
因此,当我们在查找某个数据的时候,只要从根节点开始遍历,大于根节点在左子树,小于根节点在右子树。很快就可以找到。
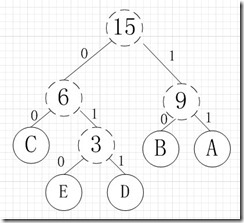
而且,在存储数据的时候利用哈夫曼树也可以对数据进行压缩。例如:A B C D E 这几个字母,他们的权值分别是5,4,3,2,1.我们在进行存储的时候就可以如图利用他们的哈弗曼编码对数据进行压缩。
下面是我写的哈弗曼编码的java代码,其中实现了建树,和遍历输出哈弗曼编码
package Sameple0505哈弗曼树;
/**
* 实现哈弗曼树的主要类
* @author Administrator
*
*/
public class Test{
private Node[] leaf =null;//该树的叶节点数组
private int length=0;//叶节点数组的长度
private int size=0;
private int count=0;//用来记录用户输入元素的个数
private Node result =null;//初始化Node
public Node getRoot(){
return result;
}
public Test(int size){
this.size=size;
leaf=new Node[this.size];
}
public Test(){}
/**
* 给叶节点数组添加值
* @param data 添加进来的叶节点内容
* @param weight 添加进来的叶节点的权值
*/
public void addNode(Object data,int weight){
Node temp =new Node(data,weight);
leaf[length++]=temp;
}
/**
* 给节点进行冒泡排序,从小到大排序,返回排好序的数组
* @param nodes
* @return
*/
public Node[] SortNode(Node[] nodes){
for(int i=0;i<nodes.length;i++){
for(int j=i+1;j<nodes.length;j++){
if(nodes[i].getwgt()>nodes[j].getwgt()){
Node tem=nodes[i];
nodes[i]=nodes[j];
nodes[j]=tem;
}
}
}
return nodes;
}
/**
* 建立哈弗曼树,从下往上建树
* @return
*/
public Node createTree(){
//判断哈弗曼树是否建好,如果建好则只剩根节点,length为1
while(length>1){
leaf=SortNode(leaf);//先按权值排序
//新节点的权值为左右节点之和
result=new Node(leaf[0].getwgt()+leaf[1].getwgt());
//分别给左右节点设置父节点
leaf[0].setFather(result);
leaf[1].setFather(result);
result.setRight(leaf[0]);//第二个元素为左节点,左边大,右边小
leaf[0].setPosition(0);//添加位置参数
result.setLeft(leaf[1]);//设置第一个元素为右节点
leaf[1].setPosition(1);//添加位置参数
leaf=newNode(leaf, 2);
length--;
leaf[length-1]=result;
}
System.out.println(result.getwgt());
return result;
}
/**
* 建树过程中不断减少的的数组
* @param nodes 新的数组
* @param num 减少的个数
* @return
*/
public Node[] newNode(Node[] nodes,int num){
Node[] newnodes=new Node[nodes.length-num+1];
for (int i = 0; i < nodes.length-num; i++) {
newnodes[i]=nodes[i+num];
}
return newnodes;
}
/**
* 从根节点开始遍历哈弗曼树,打印出叶节点上字母的哈弗曼编码
* @param args
*/
public void printhfm(Node leaf){
if (leaf.getLeft()==null&&leaf.getRight()==null) {
//输出叶节点的内容
System.out.println(leaf.getData()+"的哈弗曼编码是: ");
String posString="";//储存哈弗曼编码
while(leaf.getFather()!=null){
posString=leaf.getPosition()+posString;
leaf=leaf.getFather();
}
System.out.println(posString);
}else {
printhfm(leaf.getLeft());
printhfm(leaf.getRight());
}
}
/**
*包装方法
*/
public void showcode(){
Node temp=createTree();
printhfm(temp);
}
}
这是哈夫曼树的节点类:
package Sameple0505哈弗曼树;
/**
* 二叉树节点类
* @author 邵珂
*
*/
public class Node {
private Object data;//节点的内容
private int weight;//节点的权值
private Node father=null;//父节点
private Node left=null;//左孩子
private Node right=null;//右孩子
private String position=null;//设置该节点在父节点的位置,左边添加1,右边添加0
/**
* 重写构造方法,创建叶节点时使用
* @param data 传入的叶节点的内容
* @param weight 叶节点的权值
*/
public Node(Object data,int weight) {
this.data = data;
this.weight=weight;
}
/**
* 重写构造方法,创建非叶结点时使用
* @param weight 权值
*/
public Node(int weight){
this.weight=weight;
}
/**
* 默认的构造方法
*/
public Node(){}
/**
* 返回该节点存储的内容
* @return
*/
public Object getData() {
return data;
}
/**
* 返回该节点的权值
* @return
*/
public int getwgt(){
return weight;
}
/**
* 返回该节点的父节点
* @return
*/
public Node getFather() {
return father;
}
/**
* 设置该节点的父节点
* @param father 父节点
*/
public void setFather(Node father) {
this.father = father;
}
/**
* 返回该节点的左孩子
* @return
*/
public Node getLeft() {
return left;
}
/**
* 设置该节点的左孩子
* @param left
*/
public void setLeft(Node left) {
this.left = left;
}
/**
* 返回该节点的右孩子
* @return
*/
public Node getRight() {
return right;
}
/**
* 设置该节点的右孩子
* @param right
*/
public void setRight(Node right) {
this.right = right;
}
/**
* 获取该节点是处于父节点的左边还是右边
* @return
*/
public String getPosition() {
return position;
}
/**
* 设置该节点是在父节点的左边还是右边,左边传1,右边传0
* @param position
*/
public void setPosition(int position) {
this.position = ""+position;
}
}






相关推荐
哈夫曼树是一种在计算机科学中广泛使用的数据结构,尤其在数据压缩领域有着重要的应用。本实验报告主要探讨了如何运用哈夫曼树对文本文件进行编码和解压缩,以实现无损数据压缩。 首先,我们需要理解哈夫曼树的基本...
哈夫曼树(Huffman Tree),也称为最优二叉树,是数据压缩领域中的一个重要概念。它是基于贪心策略的一种数据结构,用于构建一种特殊的二叉树,使得带权路径长度最短,从而达到编码效率最高。哈夫曼树的核心思想是...
哈夫曼树的应用——数据结构课程设计 哈夫曼树是一种特殊的二叉树,它的每个叶子节点都对应一个权值,树的构建是根据权值的大小进行排序的。哈夫曼树的应用非常广泛,例如数据压缩、编码、解码等。 在数据结构课程...
"数据结构哈夫曼树PPT学习教案.pptx" 哈夫曼树是一种特殊的二叉树,它的带权路径长度最小。哈夫曼树的构造是数据结构中的一种重要算法,广泛应用于数据压缩、编码和决策树等领域。 一、基本术语 在哈夫曼树中,...
哈夫曼树是一种特殊的二叉树,用于解决数据编码和压缩问题,特别是在数据通信和文件压缩领域广泛应用。哈夫曼编码是一种高效的前缀编码方法,它根据数据出现频率分配最短的二进制码,频繁出现的字符拥有较短的编码,...
数据结构课程设计的目标是让学生能够灵活运用所学的数据结构知识,特别是哈夫曼树这一重要概念,来解决实际问题。哈夫曼树是一种特殊的二叉树,常用于数据压缩和编码,通过构建最小带权路径长度的二叉树,使得频率高...
数据结构中的哈夫曼树(Huffman Tree),也称为最优二叉树,是一种特殊的二叉树,主要用于数据的编码压缩。哈夫曼树是通过哈夫曼编码(Huffman Coding)来实现的,这是一种用于无损数据压缩的算法。在这个算法中,...
哈夫曼树与哈夫曼编码是数据结构和算法领域中的一个重要概念,广泛应用于数据压缩、文本编码以及优先队列等场景。哈夫曼编码是一种特殊的前缀编码方法,能够为字符提供一种高效的二进制表示,使得频繁出现的字符具有...
哈夫曼树及哈夫曼编码译码的实现 哈夫曼树是一种特殊的二叉树,它的每个节点的权重是其所有子节点的权重之和。哈夫曼树的应用非常广泛,如数据压缩、编码、译码等。 哈夫曼树的存储结构 哈夫曼树的存储结构可以...
从终端读入字符集大小n,以及n个字符和n个权值,建立哈夫曼树并将它存于文件hfmTree中.将已在内存中的哈夫曼树以直观的方式(比如树)显示在终端上; 2.利用已经建好的哈夫曼树(如不在内存,则从文件htmTree中读入...
### 数据结构:哈夫曼树上机实验 #### 实验目的 本次实验旨在通过实际编程操作,加深学生对哈夫曼树(又称最优二叉树)的理解与掌握,熟悉哈夫曼树的构造过程及其应用。 #### 实验背景 哈夫曼树是一种带权路径长度...
根据给定的文件信息,我们可以深入探讨哈夫曼树(Huffman Tree)的基本操作与实现。哈夫曼树是一种在编码领域广泛应用的数据结构,主要用于数据压缩中的编码算法,特别是无损数据压缩。以下是对该代码及其功能的详细...
哈夫曼树的编译码器 哈夫曼树是一种特殊的二叉树,它的叶子结点权值和内部结点权值的关系满足某些特定的条件,常用于数据压缩和编码。在本文中,我们将使用 C 语言实现哈夫曼树的编译码器,包括建立哈夫曼树、...
哈夫曼树是一种特殊的二叉树,也称为最优二叉树或最小带权路径长度树。在信息编码领域,哈夫曼树常用于创建哈夫曼编码,这是一种用于数据压缩的有效方法。它通过构建一种特殊的树结构,使得树中每个叶子节点代表一个...
根据给定的信息,本文将详细解析哈夫曼树的实现及其相关知识点,包括类的定义、构造过程以及编码方法。 ### 哈夫曼树的基本概念 哈夫曼树(Huffman Tree),又称最优二叉树,是一种带权路径长度最短的二叉树,在...
哈夫曼树(Huffman Tree)和哈夫曼编码(Huffman Coding)是数据压缩领域中的基础算法,它们主要用于无损数据压缩。哈夫曼编码是一种可变长度的前缀编码,通过为每个字符分配一个唯一的二进制码,使得出现频率高的...
void HuffmanCoding(HuffmanTree &HT,HuffmanCode &HC,int *w,int num)//w存放n个字符的权值(均>0),构造哈夫曼树HT,并求出n个字符的哈弗曼编码HC { int i,m,c,s1,s2,start,f; HuffmanTree p; char* cd; if...
哈夫曼树程序设计问题 哈夫曼树是一种特殊的二叉树,它的每个节点的权重都是其左右子树的权重之和。哈夫曼树的主要应用是用于数据压缩,特别是文本压缩。哈夫曼树的构建过程是从叶子节点开始,逐渐构建树形结构,...
哈夫曼树(Huffman Tree),也称为最优二叉树,是数据压缩中的一种关键算法。它是基于贪心策略构建的,用于实现哈夫曼编码(Huffman Coding),这是一种无损数据压缩方法。在C++中实现哈夫曼树压缩与解压涉及到几个...
哈夫曼树是一种特殊的二叉树,主要用于数据压缩和编码,尤其在文本传输中能有效减少数据量。它的构建基于赫夫曼编码的概念,通过构建一个具有特定特性的二叉树来实现对字符的编码和解码。 哈夫曼树的构造过程可以...