ه¹³è،،ن؛Œهڈ‰و ‘هڈˆç§°AVLو ‘م€‚ه®ƒوˆ–者وک¯é¢—ç©؛و ‘,وˆ–者وک¯ه…·وœ‰ن¸‹هˆ—و€§è´¨çڑ„ن؛Œهڈ‰و ‘ï¼ڑه®ƒçڑ„ه·¦هگو ‘ه’Œهڈ³هگو ‘都وک¯ه¹³è،،ن؛Œهڈ‰و ‘,ن¸”ه·¦هگو ‘ه’Œهڈ³هگو ‘çڑ„و·±ه؛¦ن¹‹ه·®çڑ„ç»ه¯¹ه€¼ن¸چ超è؟‡1م€‚è‹¥ه°†ن؛Œهڈ‰و ‘èٹ‚点çڑ„ه¹³è،،ه› هگBFه®ڑن¹‰ن¸؛该èٹ‚点çڑ„ه·¦هگو ‘çڑ„و·±ه؛¦ه‡ڈهژ»ه®ƒçڑ„هڈ³هگو ‘çڑ„و·±ه؛¦ï¼Œهˆ™ه¹³è،،ن؛Œهڈ‰و ‘ن¸ٹو‰€وœ‰èٹ‚点çڑ„ه¹³è،،ه› هگهڈھهڈ¯èƒ½ن¸؛-1,0,1.هڈھè¦پن؛Œهڈ‰و ‘ن¸ٹوœ‰ن¸€ن¸ھèٹ‚点çڑ„ه¹³è،،ه› هگçڑ„ç»ه¯¹ه€¼ه¤§ن؛ژ1,那ن¹ˆè؟™é¢—ه¹³è،،ن؛Œهڈ‰و ‘ه°±ه¤±هژ»ن؛†ه¹³è،،م€‚
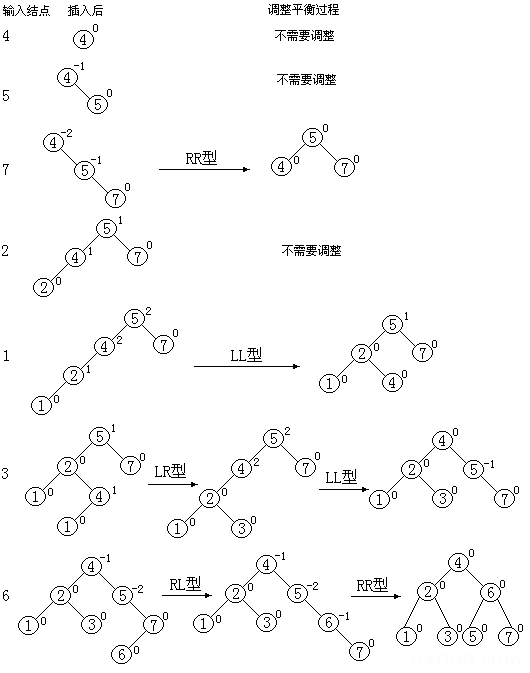
هپ‡è®¾وˆ‘ن»¬ه·²ç»ڈوœ‰و£µه¹³è،،ن؛Œهڈ‰و ‘,çژ°هœ¨è®©وˆ‘ن»¬و¥çœ‹çœ‹وڈ’ه…¥èٹ‚点هگژ,هژںو¥èٹ‚点ه¤±هژ»ه¹³è،،هگژ,وˆ‘ن»¬è؟›è،Œé€‰و‹©çڑ„ه¤„çگ†و–¹ه¼ڈم€‚
آ
ه¹³è،،ن؛Œهڈ‰و ‘ه¤ڑ用ن؛ژوں¥و‰¾و•°وچ®ï¼Œو‰€ن»¥ه¹³è،،ن؛Œهڈ‰و ‘هڈˆوک¯é¢—ن؛Œهڈ‰وژ’ه؛ڈو ‘م€‚
é‚£ن¹ˆه¦‚ن½•هˆ›ه»؛ن¸€é¢—ه¹³è،،ن؛Œهڈ‰و ‘ه‘¢ï¼ں
هˆ›ه»؛ه¹³è،،ن؛Œهڈ‰و ‘,وˆ‘ن»¬é‡‡ç”¨ن¾و¬،وڈ’ه…¥èٹ‚点çڑ„و–¹ه¼ڈè؟›è،Œم€‚而ه¹³è،،ن؛Œهڈ‰و ‘ن¸ٹوڈ’ه…¥èٹ‚点采用递ه½’çڑ„و–¹ه¼ڈè؟›è،Œم€‚递ه½’ç®—و³•ه¦‚ن¸‹ï¼ڑ
(1)آ آ آ آ آ آ 若该و ‘ن¸؛ن¸€ç©؛و ‘,那ن¹ˆوڈ’ه…¥ن¸€ن¸ھو•°وچ®ه…ƒç´ ن¸؛eçڑ„و–°èٹ‚点ن½œن¸؛ه¹³è،،ن؛Œهڈ‰و ‘çڑ„و ¹èٹ‚点,و ‘çڑ„é«که؛¦ه¢هٹ 1م€‚
(2)آ آ آ آ آ آ è‹¥ه¾…وڈ’ه…¥çڑ„و•°وچ®ه…ƒç´ eه’Œه¹³è،،ن؛Œهڈ‰و ‘(BBST)çڑ„و ¹èٹ‚点çڑ„ه…³é”®ه—相ç‰ï¼Œé‚£ن¹ˆه°±ن¸چ需è¦پè؟›è،Œوڈ’ه…¥و“چن½œم€‚
(3)آ آ آ آ آ آ è‹¥ه¾…وڈ’ه…¥çڑ„ه…ƒç´ eو¯”ه¹³è،،ن؛Œهڈ‰و ‘(BBST)çڑ„و ¹èٹ‚点çڑ„ه…³é”®ه—ه°ڈ,而ن¸”هœ¨BBSTçڑ„ه·¦هگو ‘ن¸ن¹ںن¸چهکهœ¨ه’Œeوœ‰ç›¸هگŒه…³é”®ه—çڑ„èٹ‚点,هˆ™ه°†eوڈ’ه…¥هœ¨BBSTçڑ„ه·¦هگو ‘ن¸ٹ,ه¹¶ن¸”ه½“وڈ’ه…¥ن¹‹هگژçڑ„ه·¦هگو ‘و·±ه؛¦ه¢هٹ 1و—¶ï¼Œهˆ†هˆ«ه°±ن¸‹هˆ—وƒ…ه†µه¤„çگ†ن¹‹م€‚
(a)آ آ آ آ BBSTçڑ„و ¹èٹ‚点çڑ„ه¹³è،،ه› هگن¸؛-1(هڈ³هگو ‘çڑ„و·±ه؛¦ه¤§ن؛ژه·¦هگو ‘çڑ„و·±ه؛¦ï¼‰ï¼ڑهˆ™ه°†و ¹èٹ‚点çڑ„ه¹³è،،ه› هگو›´و”¹ن¸؛0,BBSTçڑ„و·±ه؛¦ن¸چهڈکï¼›
(b)آ آ آ آ BBSTçڑ„و ¹èٹ‚点çڑ„ه¹³è،،ه› هگن¸؛0(ه·¦هڈ³هگو ‘çڑ„و·±ه؛¦ç›¸ç‰ï¼‰ï¼ڑهˆ™ه°†و ¹èٹ‚点çڑ„ه¹³è،،ه› هگن؟®و”¹ن¸؛1,BBSTçڑ„و·±ه؛¦ه¢هٹ 1ï¼›
(c)آ آ آ آ BBSTçڑ„و ¹èٹ‚点çڑ„ه¹³è،،ه› هگن¸؛1(ه·¦هگو ‘çڑ„و·±ه؛¦ه¤§ن؛ژهڈ³هگو ‘çڑ„و·±ه؛¦ï¼‰ï¼ڑè‹¥BBSTçڑ„ه·¦هگو ‘و ¹èٹ‚点çڑ„ه¹³è،،ه› هگن¸؛1,هˆ™éœ€è¦پè؟›è،Œهچ•هگ‘هڈ³و—‹è½¬ه¹³è،،ه¤„çگ†ï¼Œه¹¶ن¸”هœ¨هڈ³و—‹ه¤„çگ†هگژ,ه°†و ¹èٹ‚点ه’Œه…¶هڈ³هگو ‘و ¹èٹ‚点çڑ„ه¹³è،،ه› هگو›´و”¹ن¸؛0,و ‘çڑ„و·±ه؛¦ن¸چهڈکï¼›
è‹¥BBSTçڑ„ه·¦هگو ‘و ¹èٹ‚点çڑ„ه¹³è،،ه› هگن¸؛-1,هˆ™éœ€è؟›è،Œه…ˆهگ‘ه·¦ï¼Œهگژهگ‘هڈ³çڑ„هڈŒهگ‘و—‹è½¬ه¹³è،،ه¤„çگ†ï¼Œه¹¶ن¸”هœ¨و—‹è½¬ه¤„çگ†ن¹‹هگژ,ن؟®و”¹و ¹èٹ‚点ه’Œه…¶ه·¦ï¼Œهڈ³هگو ‘و ¹èٹ‚点çڑ„ه¹³è،،ه› هگ,و ‘çڑ„و·±ه؛¦ن¸چهڈکï¼›
(4)آ آ آ آ آ آ è‹¥eçڑ„ه…³é”®ه—ه¤§ن؛ژBBSTçڑ„و ¹èٹ‚点çڑ„ه…³é”®ه—,而ن¸”هœ¨BBSTçڑ„هڈ³هگو ‘ن¸ن¸چهکهœ¨ه’Œeوœ‰ç›¸هگŒه…³é”®ه—çڑ„èٹ‚点,هˆ™ه°†eوڈ’ه…¥هˆ°BBSTçڑ„هڈ³هگو ‘ن¸ٹ,ه¹¶ن¸”ه½“وڈ’ه…¥ن¹‹هگژçڑ„هڈ³هگو ‘و·±ه؛¦هٹ 1و—¶ï¼Œهˆ†هˆ«ه°±ن¸چهگŒçڑ„وƒ…ه†µه¤„çگ†ن¹‹م€‚
(a)آ آ آ آ آ آ BBSTçڑ„و ¹èٹ‚点çڑ„ه¹³è،،ه› هگوک¯1(ه·¦هگو ‘çڑ„و·±ه؛¦ه¤§ن؛ژهڈ³هگو ‘çڑ„و·±ه؛¦ï¼‰ï¼ڑهˆ™ه°†و ¹èٹ‚点çڑ„ه¹³è،،ه› هگن؟®و”¹ن¸؛0,BBSTçڑ„و·±ه؛¦ن¸چهڈکï¼›
(b)آ آ آ آ آ آ BBSTçڑ„و ¹èٹ‚点çڑ„ه¹³è،،ه› هگوک¯0(ه·¦هڈ³هگو ‘çڑ„و·±ه؛¦ç›¸ç‰ï¼‰ï¼ڑهˆ™ه°†و ¹èٹ‚点çڑ„ه¹³è،،ه› هگن؟®و”¹ن¸؛-1,و ‘çڑ„و·±ه؛¦هٹ 1ï¼›
(c)آ آ آ آ آ آ BBSTçڑ„و ¹èٹ‚点çڑ„ه¹³è،،ه› هگن¸؛-1(هڈ³هگو ‘çڑ„و·±ه؛¦ه¤§ن؛ژه·¦هگو ‘çڑ„و·±ه؛¦ï¼‰ï¼ڑè‹¥BBSTçڑ„هڈ³هگو ‘و ¹èٹ‚点çڑ„ه¹³è،،ه› هگن¸؛1,هˆ™éœ€è¦پè؟›è،Œن¸¤و¬،选و‹©ï¼Œç¬¬ن¸€و¬،ه…ˆهگ‘هڈ³و—‹è½¬ï¼Œه†چهگ‘ه·¦و—‹è½¬ه¤„çگ†ï¼Œه¹¶ن¸”هœ¨و—‹è½¬ه¤„çگ†ن¹‹هگژ,ن؟®و”¹و ¹èٹ‚点ه’Œه…¶ه·¦ï¼Œهڈ³هگو ‘و ¹èٹ‚点çڑ„ه¹³è،،ه› هگ,و ‘çڑ„و·±ه؛¦ن¸چهڈکï¼›
è‹¥BBSTçڑ„هڈ³هگو ‘و ¹èٹ‚点çڑ„ه¹³è،،ه› هگن¸؛1,هˆ™éœ€è¦پè؟›è،Œن¸€و¬،هگ‘ه·¦çڑ„و—‹è½¬ه¤„çگ†ï¼Œه¹¶ن¸”هœ¨ه·¦و—‹ن¹‹هگژ,و›´و–°و ¹èٹ‚点ه’Œه…¶ه·¦ï¼Œهڈ³هگو ‘و ¹èٹ‚点çڑ„ه¹³è،،ه› هگ,و ‘çڑ„و·±ه؛¦ن¸چهڈکï¼›
آ
ن¸‹é¢é™„ن¸ٹوœ¬ن؛؛çڑ„ن»£ç پï¼ڑ
آ
- #includeآ <stdio.h>آ آ
- #includeآ <stdlib.h>آ آ
- /************************************************************************/آ آ
- /*آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ ه¹³è،،ن؛Œهڈ‰و ‘---AVLآ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ */آ آ
- /************************************************************************/آ آ
- #defineآ LHآ +1آ آ
- #defineآ EHآ آ 0آ آ
- #defineآ RHآ -1آ آ
- typedefآ intآ ElemType;آ آ
- typedefآ structآ BSTNode{آ آ
- آ آ آ آ ElemTypeآ data;آ آ
- آ آ آ آ intآ bf;//balanceآ flagآ آ
- آ آ آ آ structآ BSTNodeآ *lchild,*rchild;آ آ
- }*PBSTree;آ آ
- آ آ
- voidآ R_Rotate(PBSTree*آ p)آ آ
- {آ آ
- آ آ آ آ PBSTreeآ lcآ =آ (*p)->lchild;آ آ
- آ آ آ آ (*p)->lchildآ =آ lc->rchild;آ آ
- آ آ آ آ lc->rchildآ =آ *p;آ آ
- آ آ آ آ *pآ =آ lc;آ آ
- }آ آ
- آ آ
- voidآ L_Rotate(PBSTree*آ p)آ آ
- {آ آ
- آ آ آ آ PBSTreeآ rcآ =آ (*p)->rchild;آ آ
- آ آ آ آ (*p)->rchildآ =آ rc->lchild;آ آ
- آ آ آ آ rc->lchildآ =آ *p;آ آ
- آ آ آ آ *pآ =آ rc;آ آ
- }آ آ
- آ آ
- voidآ LeftBalance(PBSTree*آ T)آ آ
- {آ آ
- آ آ آ آ PBSTreeآ lc,rd;آ آ
- آ آ آ آ lcآ =آ (*T)->lchild;آ آ
- آ آ آ آ switchآ (lc->bf)آ آ
- آ آ آ آ {آ آ
- آ آ آ آ caseآ LH:آ آ
- آ آ آ آ آ آ آ آ (*T)->bfآ =آ lc->bfآ =آ EH;آ آ
- آ آ آ آ آ آ آ آ R_Rotate(T);آ آ
- آ آ آ آ آ آ آ آ break;آ آ
- آ آ آ آ caseآ RH:آ آ
- آ آ آ آ آ آ آ آ rdآ =آ lc->rchild;آ آ
- آ آ آ آ آ آ آ آ switch(rd->bf)آ آ
- آ آ آ آ آ آ آ آ {آ آ
- آ آ آ آ آ آ آ آ caseآ LH:آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ (*T)->bfآ =آ RH;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ lc->bfآ =آ EH;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ break;آ آ
- آ آ آ آ آ آ آ آ caseآ EH:آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ (*T)->bfآ =آ lc->bfآ =آ EH;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ break;آ آ
- آ آ آ آ آ آ آ آ caseآ RH:آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ (*T)->bfآ =آ EH;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ lc->bfآ =آ LH;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ break;آ آ
- آ آ آ آ آ آ آ آ }آ آ
- آ آ آ آ آ آ آ آ rd->bfآ =آ EH;آ آ
- آ آ آ آ آ آ آ آ L_Rotate(&(*T)->lchild);آ آ
- آ آ آ آ آ آ آ آ R_Rotate(T);آ آ
- آ آ آ آ آ آ آ آ break;آ آ
- آ آ آ آ }آ آ
- }آ آ
- آ آ
- voidآ RightBalance(PBSTree*آ T)آ آ
- {آ آ
- آ آ آ آ PBSTreeآ lc,rd;آ آ
- آ آ آ آ lc=آ (*T)->rchild;آ آ
- آ آ آ آ switchآ (lc->bf)آ آ
- آ آ آ آ {آ آ
- آ آ آ آ caseآ RH:آ آ
- آ آ آ آ آ آ آ آ (*T)->bfآ =آ lc->bfآ =آ EH;آ آ
- آ آ آ آ آ آ آ آ L_Rotate(T);آ آ
- آ آ آ آ آ آ آ آ break;آ آ
- آ آ آ آ caseآ LH:آ آ
- آ آ آ آ آ آ آ آ rdآ =آ lc->lchild;آ آ
- آ آ آ آ آ آ آ آ switch(rd->bf)آ آ
- آ آ آ آ آ آ آ آ {آ آ
- آ آ آ آ آ آ آ آ caseآ LH:آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ (*T)->bfآ =آ EH;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ lc->bfآ =آ RH;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ break;آ آ
- آ آ آ آ آ آ آ آ caseآ EH:آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ (*T)->bfآ =آ lc->bfآ =آ EH;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ break;آ آ
- آ آ آ آ آ آ آ آ caseآ RH:آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ (*T)->bfآ =آ EH;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ lc->bfآ =آ LH;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ break;آ آ
- آ آ آ آ آ آ آ آ }آ آ
- آ آ آ آ آ آ آ آ rd->bfآ =آ EH;آ آ
- آ آ آ آ آ آ آ آ R_Rotate(&(*T)->rchild);آ آ
- آ آ آ آ آ آ آ آ L_Rotate(T);آ آ
- آ آ آ آ آ آ آ آ break;آ آ
- آ آ آ آ }آ آ
- }آ آ
- آ آ
- intآ InsertAVL(PBSTree*آ T,ElemTypeآ e,bool*آ taller)آ آ
- {آ آ
- آ آ آ آ ifآ ((*T)==NULL)آ آ
- آ آ آ آ {آ آ
- آ آ آ آ آ آ آ آ (*T)=(PBSTree)malloc(sizeof(BSTNode));آ آ
- آ آ آ آ آ آ آ آ (*T)->bfآ =آ EH;آ آ
- آ آ آ آ آ آ آ آ (*T)->dataآ =آ e;آ آ
- آ آ آ آ آ آ آ آ (*T)->lchildآ =آ NULL;آ آ
- آ آ آ آ آ آ آ آ (*T)->rchildآ =آ NULL;آ آ
- آ آ آ آ }آ آ
- آ آ آ آ elseآ ifآ (eآ ==آ (*T)->data)آ آ
- آ آ آ آ {آ آ
- آ آ آ آ آ آ آ آ *tallerآ =آ false;آ آ
- آ آ آ آ آ آ آ آ returnآ 0;آ آ
- آ آ آ آ }آ آ
- آ آ آ آ elseآ ifآ (eآ <آ (*T)->data)آ آ
- آ آ آ آ {آ آ
- آ آ آ آ آ آ آ آ if(!InsertAVL(&(*T)->lchild,e,taller))آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ returnآ 0;آ آ
- آ آ آ آ آ آ آ آ if(*taller)آ آ
- آ آ آ آ آ آ آ آ {آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ switchآ ((*T)->bf)آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ {آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ caseآ LH:آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ LeftBalance(T);آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ *tallerآ =آ false;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ break;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ caseآ آ EH:آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ (*T)->bfآ =آ LH;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ *tallerآ =آ true;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ break;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ caseآ RH:آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ (*T)->bfآ =آ EH;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ *tallerآ =آ false;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ break;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ }آ آ
- آ آ آ آ آ آ آ آ }آ آ
- آ آ آ آ }آ آ
- آ آ آ آ elseآ آ
- آ آ آ آ {آ آ
- آ آ آ آ آ آ آ آ if(!InsertAVL(&(*T)->rchild,e,taller))آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ returnآ 0;آ آ
- آ آ آ آ آ آ آ آ ifآ (*taller)آ آ
- آ آ آ آ آ آ آ آ {آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ switchآ ((*T)->bf)آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ {آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ caseآ LH:آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ (*T)->bfآ =آ EH;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ *tallerآ =آ false;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ break;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ caseآ EH:آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ (*T)->bfآ =آ RH;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ *tallerآ =آ true;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ break;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ caseآ آ RH:آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ RightBalance(T);آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ *tallerآ =آ false;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ break;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ }آ آ
- آ آ آ آ آ آ آ آ }آ آ
- آ آ آ آ }آ آ
- آ آ آ آ returnآ 1;آ آ
- }آ آ
- آ آ
- boolآ FindNode(PBSTreeآ root,ElemTypeآ e,PBSTree*آ pos)آ آ
- {آ آ
- آ آ آ آ PBSTreeآ ptآ =آ root;آ آ
- آ آ آ آ (*pos)آ =آ NULL;آ آ
- آ آ آ آ while(pt)آ آ
- آ آ آ آ {آ آ
- آ آ آ آ آ آ آ آ ifآ (pt->dataآ ==آ e)آ آ
- آ آ آ آ آ آ آ آ {آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ //و‰¾هˆ°èٹ‚点,posوŒ‡هگ‘该èٹ‚点ه¹¶è؟”ه›trueآ آ
- آ آ آ آ آ آ آ آ آ آ آ آ (*pos)آ =آ pt;آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ returnآ true;آ آ
- آ آ آ آ آ آ آ آ }آ آ
- آ آ آ آ آ آ آ آ elseآ ifآ (pt->data>e)آ آ
- آ آ آ آ آ آ آ آ {آ آ
- آ آ آ آ آ آ آ آ آ آ آ آ ptآ =آ pt->lchild;آ آ
- آ آ آ آ آ آ آ آ }آ آ
- آ آ آ آ آ آ آ آ elseآ آ
- آ آ آ آ آ آ آ آ آ آ آ آ ptآ =آ pt->rchild;آ آ
- آ آ آ آ }آ آ
- آ آ آ آ returnآ false;آ آ
- }آ آ
- voidآ InorderTra(PBSTreeآ root)آ آ
- {آ آ
- آ آ آ آ if(root->lchild)آ آ
- آ آ آ آ آ آ آ آ InorderTra(root->lchild);آ آ
- آ آ آ آ printf("%dآ ",root->data);آ آ
- آ آ آ آ if(root->rchild)آ آ
- آ آ آ آ آ آ آ آ InorderTra(root->rchild);آ آ
- }آ آ
- آ آ
- intآ main()آ آ
- {آ آ
- آ آ آ آ intآ i,nArr[]آ =آ {1,23,45,34,98,9,4,35,23};آ آ
- آ آ آ آ PBSTreeآ root=NULL,pos;آ آ
- آ آ آ آ boolآ taller;آ آ
- آ آ آ آ forآ (i=0;i<9;i++)آ آ
- آ آ آ آ {آ آ
- آ آ آ آ آ آ آ آ InsertAVL(&root,nArr[i],&taller);آ آ
- آ آ آ آ }آ آ
- آ آ آ آ InorderTra(root);آ آ
- آ آ آ آ if(FindNode(root,103,&pos))آ آ
- آ آ آ آ آ آ آ آ printf("\n%d\n",pos->data);آ آ
- آ آ آ آ elseآ آ
- آ آ آ آ آ آ آ آ printf("\nNotآ findآ thisآ Node\n");آ آ
- آ آ آ آ returnآ 0;آ آ
- }آ آ
转载L:http://blog.csdn.net/w170532934/article/details/7571281
آ
آ






相ه…³وژ¨èچگ
ه¹³è،،ن؛Œهڈ‰و ‘وک¯ن¸€ç§چ特و®ٹç±»ه‹çڑ„ن؛Œهڈ‰و ‘,ه®ƒçڑ„ه·¦هڈ³ن¸¤ن¸ھهگو ‘çڑ„é«که؛¦ه·®çڑ„ç»ه¯¹ه€¼ن¸چ超è؟‡1,ه¹¶ن¸”ه·¦هڈ³ن¸¤ن¸ھهگو ‘都وک¯ن¸€و£µه¹³è،،ن؛Œهڈ‰و ‘م€‚è؟™ç§چو•°وچ®ç»“و„çڑ„ن¸»è¦پç›®çڑ„وک¯ن¸؛ن؛†ن؟وŒپو•°وچ®çڑ„ه¹³è،،هˆ†ه¸ƒï¼Œن»ژ而ن؟è¯پهœ¨وڈ’ه…¥م€پهˆ 除ه’Œوں¥و‰¾و“چن½œن¸çڑ„و•ˆçژ‡م€‚ ...
ه¹³è،،ن؛Œهڈ‰و ‘Javaه®çژ°ï¼Œه¹³è،،ن؛Œهڈ‰و ‘Javaه®çژ°ï¼Œه¹³è،،ن؛Œهڈ‰و ‘Javaه®çژ°ï¼Œه¹³è،،ن؛Œهڈ‰و ‘Javaه®çژ°ï¼Œ
ه¦‚ن½•ه°†ن¸€و£µن¸چه¹³è،،çڑ„ن؛Œهڈ‰و ‘ه¹³è،،ه‘¢ï¼ˆه·¦هڈ³هگو ‘çڑ„é«که؛¦ه·®ه€¼ه¾ˆه¤§ï¼‰ï¼ںن¸چç®،وک¯ن»ژو ¹èٹ‚点è؟کوک¯ن»ژوœ€ه°ڈن¸چه¹³è،،ن؛Œهڈ‰و ‘ه¼€ه§‹و—‹è½¬ه¹³è،،,هڈ¯èƒ½éƒ½ن¼ڑه‡؛çژ°ن¸€و¬،éپچهژ†و— و³•ه¹³è،،çڑ„وƒ…ه†µï¼ˆن¼ڑه‡؛çژ°è؟é”پهڈچه؛”)م€‚ ه¦‚وœو•´و£µو ‘هڈ¯ن»¥هپڑهˆ°éڑڈو—¶ه®Œه…¨ه¹³è،،ه¤„çگ†ï¼Œ...
"ه¹³è،،ن؛Œهڈ‰و ‘و—¶é—´ه¤چو‚ه؛¦è®،ç®—1" هœ¨è®،ç®—وœ؛科ه¦ن¸ï¼Œه¹³è،،ن؛Œهڈ‰و ‘وک¯ن¸€ç§چ特و®ٹçڑ„ن؛Œهڈ‰و ‘و•°وچ®ç»“و„,ه®ƒçڑ„و—¶é—´ه¤چو‚ه؛¦è®،ç®—وک¯éه¸¸é‡چè¦پçڑ„م€‚ن¸‹é¢وˆ‘ن»¬ه°†è¯¦ç»†ن»‹ç»چه¹³è،،ن؛Œهڈ‰و ‘çڑ„و—¶é—´ه¤چو‚ه؛¦è®،ç®—م€‚ 首ه…ˆï¼Œè®©وˆ‘ن»¬ن؛†è§£ن»€ن¹ˆوک¯ه¹³è،،ن؛Œهڈ‰و ‘م€‚...
هœ¨IT领هںں,و•°وچ®ç»“و„وک¯è®،ç®—وœ؛科ه¦çڑ„هں؛ç،€ï¼Œè€Œه¹³è،،ن؛Œهڈ‰و ‘وک¯ه…¶ن¸ن¸€ن¸ھé‡چè¦پو¦‚ه؟µï¼Œه°¤ه…¶ه¯¹ن؛ژé«کو•ˆçڑ„و•°وچ®و£€ç´¢ه’Œهکه‚¨م€‚هœ¨è؟™ن¸ھ“و•°وچ®ç»“و„ه¹³è،،ن؛Œهڈ‰و ‘课程设è®،â€ن¸ï¼Œوˆ‘ن»¬é‡چ点وژ¢è®¨ن؛†ه¦‚ن½•ن½؟用Cè¯è¨€ه®çژ°ه¹³è،،ن؛Œهڈ‰و ‘,ه¹¶هŒ…هگ«ن؛†è¯¾ç¨‹è®¾è®،...
ه¹³è،،ن؛Œهڈ‰و ‘(Balanced Binary Tree)وک¯و•°وچ®ç»“و„ن¸çڑ„ن¸€ن¸ھé‡چè¦پو¦‚ه؟µï¼Œه°¤ه…¶هœ¨ç®—و³•è®¾è®،ه’Œو•°وچ®ه؛“ç³»ç»ںن¸هڈ‘وŒ¥ç€ه…³é”®ن½œç”¨م€‚وœ¬ه®éھŒوک¯é’ˆه¯¹ه¹؟ن¸œه·¥ن¸ڑه¤§ه¦ï¼ˆç®€ç§°â€œه¹؟ه·¥â€ï¼‰ه¦ç”ںçڑ„ن¸€و¬،و•°وچ®ç»“و„课程ه®è·µï¼Œو—¨هœ¨è®©ه¦ç”ںو·±ه…¥çگ†è§£ه¹³è،،...
ه¹³è،،ن؛Œهڈ‰و ‘وک¯ن¸€ç§چ特و®ٹçڑ„ن؛Œهڈ‰و ‘结و„,ه®ƒçڑ„ن¸»è¦پ特و€§وک¯ه·¦هڈ³هگو ‘çڑ„é«که؛¦ه·®ن¸چ超è؟‡1,ن؟è¯پن؛†و ‘çڑ„ه½¢و€په‡هŒ€ï¼Œن»ژ而هœ¨وں¥و‰¾م€پوڈ’ه…¥ه’Œهˆ 除ç‰و“چن½œن¸ٹçڑ„و•ˆçژ‡وژ¥è؟‘ن؛ژوœ€ن½³çڑ„ن؛Œهڈ‰وں¥و‰¾و ‘م€‚è؟™ç§چ特و€§ن½؟ه¾—ه¹³è،،ن؛Œهڈ‰و ‘هœ¨و•°وچ®ç»“و„ه’Œç®—و³•ن¸هچ وœ‰...
ه¹³è،،ن؛Œهڈ‰و ‘وک¯ن¸€ç§چ特و®ٹçڑ„ن؛Œهڈ‰و ‘و•°وچ®ç»“و„,ه…¶ç‰¹و€§هœ¨ن؛ژه·¦هڈ³هگو ‘çڑ„é«که؛¦ه·®ن¸چ超è؟‡1,è؟™ن½؟ه¾—هœ¨و ‘ن¸çڑ„ن»»ن½•èٹ‚点ن¸ٹè؟›è،Œوں¥و‰¾م€پوڈ’ه…¥ه’Œهˆ 除و“چن½œçڑ„و—¶é—´ه¤چو‚ه؛¦éƒ½èƒ½ن؟è¯پن¸؛O(log n)م€‚AVLو ‘وک¯وœ€و—©è¢«وڈگه‡؛çڑ„è‡ھه¹³è،،ن؛Œهڈ‰وگœç´¢و ‘,由G. M. ...
ه¹³è،،ن؛Œهڈ‰و ‘وک¯ن¸€ç§چ特و®ٹçڑ„ن؛Œهڈ‰و ‘و•°وچ®ç»“و„,ه®ƒهœ¨ن؟وŒپن؛Œهڈ‰وں¥و‰¾و ‘و€§è´¨çڑ„هگŒو—¶ï¼Œç،®ن؟ن؛†ه·¦هڈ³هگو ‘çڑ„é«که؛¦ه·®ن¸چ超è؟‡1م€‚è؟™و ·çڑ„结و„ن½؟ه¾—هœ¨ه¹³è،،ن؛Œهڈ‰و ‘ن¸çڑ„وگœç´¢م€پوڈ’ه…¥ه’Œهˆ 除و“چن½œçڑ„و—¶é—´ه¤چو‚ه؛¦éƒ½èƒ½ن؟وŒپهœ¨O(log n)çڑ„و°´ه¹³ï¼Œه¤§ه¤§وڈگé«کن؛†...
ن؛Œهڈ‰و ‘ه’Œه¹³è،،ن؛Œهڈ‰و ‘وک¯و•°وچ®ç»“و„领هںںن¸çڑ„é‡چè¦پو¦‚ه؟µï¼Œه°¤ه…¶هœ¨è®،ç®—وœ؛科ه¦ن¸ï¼Œه®ƒن»¬هœ¨و•°وچ®هکه‚¨م€پوگœç´¢ه’Œوژ’ه؛ڈç‰و–¹é¢هڈ‘وŒ¥ç€ه…³é”®ن½œç”¨م€‚è؟™é‡Œوˆ‘ن»¬ه°†و·±ه…¥وژ¢è®¨è؟™ن¸¤ç§چو•°وچ®ç»“و„هڈٹه…¶C#ه®çژ°م€‚ 首ه…ˆï¼Œن؛Œهڈ‰و ‘وک¯ن¸€ç§چ特و®ٹçڑ„و ‘ه½¢و•°وچ®ç»“و„,...
ه¹³è،،ن؛Œهڈ‰و ‘وک¯ن¸€ç§چ特و®ٹçڑ„ن؛Œهڈ‰و ‘结و„,ه®ƒçڑ„ه·¦هڈ³ن¸¤ن¸ھهگو ‘çڑ„é«که؛¦ه·®ن¸چ超è؟‡1,ه¹¶ن¸”ه·¦هڈ³ن¸¤ن¸ھهگو ‘都وک¯ن¸€و£µه¹³è،،ن؛Œهڈ‰و ‘م€‚è؟™ç§چو•°وچ®ç»“و„هœ¨è®،ç®—وœ؛科ه¦ن¸وœ‰ç€ه¹؟و³›çڑ„ه؛”用,ه°¤ه…¶وک¯هœ¨وگœç´¢م€پوژ’ه؛ڈه’Œو•°وچ®هکه‚¨ç‰é¢†هںںم€‚وœ¬و–‡ه°†è¯¦ç»†ن»‹ç»چه¹³è،،...
ه¹³è،،ن؛Œهڈ‰و ‘وک¯ن¸€ç§چ特و®ٹçڑ„ن؛Œهڈ‰و ‘و•°وچ®ç»“و„,ه®ƒهœ¨ن؟وŒپن؛Œهڈ‰وں¥و‰¾و ‘特و€§çڑ„هگŒو—¶ï¼Œé€ڑè؟‡ç‰¹ه®ڑçڑ„结و„è°ƒو•´ç–略,ç،®ن؟ن؛†و ‘çڑ„é«که؛¦ه¹³è،،م€‚è؟™و ·çڑ„设è®،ن½؟ه¾—هœ¨ه¹³è،،ن؛Œهڈ‰و ‘ن¸و‰§è،Œوڈ’ه…¥م€پهˆ 除ه’Œوں¥و‰¾ç‰و“چن½œçڑ„و—¶é—´ه¤چو‚ه؛¦هڈ¯ن»¥ن؟وŒپن¸؛O(log n),...
ه¹³è،،ن؛Œهڈ‰و ‘وک¯ن¸€ç§چ特و®ٹçڑ„ن؛Œهڈ‰و ‘结و„,ه®ƒçڑ„ه·¦هڈ³هگو ‘é«که؛¦ه·®ن¸چ超è؟‡1,ن¸”و¯ڈن¸ھèٹ‚点çڑ„ه·¦هڈ³هگو ‘都وک¯ه¹³è،،ن؛Œهڈ‰و ‘م€‚è؟™ç§چ设è®،ن½؟ه¾—هœ¨ه¹³è،،ن؛Œهڈ‰و ‘ن¸è؟›è،Œوں¥و‰¾م€پوڈ’ه…¥ه’Œهˆ 除و“چن½œçڑ„و—¶é—´ه¤چو‚ه؛¦هڈ¯ن»¥è¾¾هˆ°O(log n),وپه¤§هœ°وڈگé«کن؛†و•°وچ®و“چن½œçڑ„...
ه¹³è،،ن؛Œهڈ‰و ‘وک¯ن¸€ç§چ特و®ٹçڑ„ن؛Œهڈ‰و ‘و•°وچ®ç»“و„,ه…¶ç‰¹و€§وک¯ه·¦هڈ³هگو ‘çڑ„é«که؛¦ه·®ن¸چ超è؟‡1,è؟™ن½؟ه¾—هœ¨ه¹³è،،ن؛Œهڈ‰و ‘ن¸çڑ„وں¥و‰¾م€پوڈ’ه…¥ه’Œهˆ 除و“چن½œçڑ„و—¶é—´ه¤چو‚ه؛¦éƒ½èƒ½ن؟وŒپهœ¨O(log n)ç؛§هˆ«ï¼Œه¤§ه¤§وڈگé«کن؛†و•ˆçژ‡م€‚هœ¨وœ¬é،¹ç›®ن¸ï¼Œوˆ‘ن»¬ه°†وژ¢è®¨ه¦‚ن½•ن½؟用C++...
هœ¨و•°وچ®ç»“و„课程设è®،ن¸ï¼Œه¹³è،،ن؛Œهڈ‰و ‘çڑ„ه®çژ°وک¯ن¸€ن¸ھé‡چè¦پçڑ„ه®è·µçژ¯èٹ‚,و—¨هœ¨هٹ و·±ه¯¹و•°وچ®ç»“و„ه’Œç®—و³•çڑ„çگ†è§£م€‚ه¹³è،،ن؛Œهڈ‰و ‘وک¯ن¸€ç§چ特و®ٹçڑ„ن؛Œهڈ‰و ‘,ه®ƒç،®ن؟ن؛†ن»»ن½•èٹ‚点çڑ„ن¸¤ن¸ھهگو ‘çڑ„é«که؛¦ه·®ن¸چ超è؟‡1,ن»ژ而ن؟è¯پن؛†و“چن½œه¦‚وں¥و‰¾م€پوڈ’ه…¥ه’Œهˆ 除çڑ„...
1. هˆ©ç”¨ه¹³è،،ن؛Œهڈ‰و ‘ه®çژ°ن¸€ن¸ھهٹ¨و€پوں¥و‰¾è،¨ï¼Œه®çژ°هٹ¨و€پوں¥و‰¾è،¨çڑ„ن¸‰ç§چهں؛وœ¬هٹں能ï¼ڑوں¥و‰¾ وڈ’ه…¥ه’Œهˆ 除م€‚ 2 .هˆه§‹ï¼Œه¹³è،،ن؛Œهڈ‰و ‘ن¸؛ç©؛و ‘,و“چن½œç•Œé¢ç»™ه‡؛وں¥و‰¾ï¼Œوڈ’ه…¥ه’Œهˆ 除ن¸‰ç§چو“چن½œن¾› 选و‹©ï¼Œو¯ڈç§چو“چن½œه‡è¦پوڈگç¤؛输ه…¥ه…³é”®ه—,و¯ڈو¬،وڈ’ه…¥وˆ–هˆ 除...
ه¹³è،،ن؛Œهڈ‰و ‘وک¯ن¸€ç§چ特و®ٹçڑ„ن؛Œهڈ‰و ‘结و„,ه®ƒçڑ„ه·¦هڈ³هگو ‘é«که؛¦ه·®ن¸چ超è؟‡1,ه¹¶ن¸”ه·¦هڈ³هگو ‘都وک¯ه¹³è،،ن؛Œهڈ‰و ‘م€‚è؟™ç§چ结و„هœ¨و•°وچ®ه¤„çگ†ه’Œوگœç´¢ç®—و³•ن¸ه…·وœ‰é‡چè¦پن½œç”¨ï¼Œه› ن¸؛ه®ƒن؟è¯پن؛†وں¥و‰¾م€پوڈ’ه…¥ه’Œهˆ 除ç‰و“چن½œçڑ„و—¶é—´ه¤چو‚ه؛¦ن¸؛O(log n)م€‚ن¸‹é¢وˆ‘ن»¬...
و€»ç»“而言,ن؛Œهڈ‰و ‘وک¯هں؛ç،€ن¸”é‡چè¦پçڑ„و•°وچ®ç»“و„,ه¹³è،،ن؛Œهڈ‰و ‘ه¦‚AVLو ‘ه’Œç؛¢é»‘و ‘هˆ™é€ڑè؟‡ن؟وŒپو ‘çڑ„ه¹³è،،ن¼کهŒ–ن؛†و“چن½œو•ˆçژ‡م€‚ه¹³ه‡وں¥و‰¾é•؟ه؛¦وک¯è،،é‡ڈوں¥و‰¾و€§èƒ½çڑ„ه…³é”®وŒ‡و ‡ï¼Œè€Œن؛Œهڈ‰و ‘çڑ„هˆ 除و“چن½œهˆ™éœ€è¦پو ¹وچ®èٹ‚点çڑ„هگèٹ‚点وƒ…ه†µçپµو´»ه¤„çگ†م€‚و؛گن»£ç پ...