1.做课设的时候看了很多资料,结果很多讲的不清楚,这里转载一篇最好的,最通俗易懂的文章
转载地址: http://blog.csdn.net/lycb_gz/article/details/8201987
5.3.2 循环冗余校验检错方案
奇偶校验码只能校验一位错误,本节所要介绍的循环冗余校验码(CRC)的检错能力更强,可以检出多位错误。
1. CRC校验原理
CRC校验原理其实是很简单的问题,其根本思想就是先在要发送的帧后面附加一个二进制数(这个数就是校验码),生成一个新帧发送给接收端。
例如: 要发送 1 校验码100000001111(crc-12)
新帧就是1+100000001111 -> 1100000001111
当然,校验码不是随意的,它要使所生成的新帧能与发送端和接收端共同选定的某个特定数整除(注意,这里不是直接采用二进制除法,而是采用一种称之为“模2除法”)。到达接收端后,再把接收到的新帧除以(同样采用“模2除法”)这个选定的除数。
因为在发送端发送数据帧之前就已通过附加一个数,做了“去余”处理(也就已经能整除了),所以结果应该是没有余数。如果有余数,则表明该帧在传输过程中出现了差错。
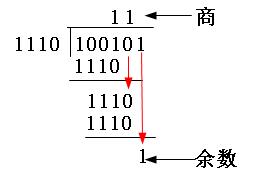
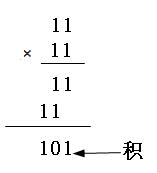
【说明】“模2除法”与“算术除法”类似,但它既不向上位借位,也不比较除数和被除数的相同位数值的大小,只要以相同位数进行相除即可。模2加法运算为:1+1=0,0+1=1,0+0=0,无进位,也无借位;模2减法运算为:1-1=0,0-1=1,1-0=1,0-0=0,也无进位,无借位。相当于二进制中的逻辑异或运算。也就是比较后,两者对应位相同则结果为“0”,不同则结果为“1”。如100101除以1110,结果得到商为11,余数为1,如图5-9左图所示。如11×11=101,如图5-9右图所示。
图5-9 “模2除法”和“模2乘法”示例
CRC校验原理步骤:
(1)先选择(可以随机选择,也可按标准选择,具体在后面介绍)一个用于在接收端进行校验时,对接收的帧进行除法运算的除数(是二进制比较特串,通常是以多项方式表示,所以CRC又称多项式编码方法,这个多项式也称之为“生成多项式”)。
(2)看所选定的除数二进制位数(假设为k位),然后在要发送的数据帧(假设为m位)后面加上k-1位“0”,然后以这个加了k-1个“0“的新帧(一共是m+k-1位)以“模2除法”方式除以上面这个除数,所得到的余数(也是二进制的比特串)就是该帧的CRC校验码,也称之为FCS(帧校验序列)。但要注意的是,余数的位数一定要是比除数位数只能少一位,哪怕前面位是0,甚至是全为0(附带好整除时)也都不能省略。
(3)再把这个校验码附加在原数据帧(就是m位的帧,注意不是在后面形成的m+k-1位的帧)后面,构建一个新帧发送到接收端,最后在接收端再把这个新帧以“模2除法”方式除以前面选择的除数,如果没有余数,则表明该帧在传输过程中没出错,否则出现了差错。
通过以上介绍,大家一定可以理解CRC校验的原理,并且不再认为很复杂吧。
从上面可以看出,CRC校验中有两个关键点:一是要预先确定一个发送端和接收端都用来作为除数的二进制比特串(或多项式);二是把原始帧与上面选定的除进行二进制除法运算,计算出FCS。前者可以随机选择,也可按国际上通行的标准选择,但最高位和最低位必须均为“1”,如在IBM的SDLC(同步数据链路控制)规程中使用的CRC-16(也就是这个除数一共是17位)生成多项式g(x)= x16 + x15 + x2 +1(对应二进制比特串为:11000000000000101);而在ISO HDLC(高级数据链路控制)规程、ITU的SDLC、X.25、V.34、V.41、V.42等中使用CCITT-16生成多项式g(x)=x16 + x15 + x5 +1(对应二进制比特串为:11000000000100001)。
2. CRC校验码的计算示例
由以上分析可知,既然除数是随机,或者按标准选定的,所以CRC校验的关键是如何求出余数,也就是CRC校验码。
下面以一个例子来具体说明整个过程。现假设选择的CRC生成多项式为G(X) = X4 + X3 + 1,要求出二进制序列10110011的CRC校验码。下面是具体的计算过程:
(1)首先把生成多项式转换成二进制数,由G(X) = X4 + X3 + 1可以知道(,它一共是5位(总位数等于最高位的幂次加1,即4+1=5),然后根据多项式各项的含义(多项式只列出二进制值为1的位,也就是这个二进制的第4位、第3位、第0位的二进制均为1,其它位均为0)很快就可得到它的二进制比特串为11001。
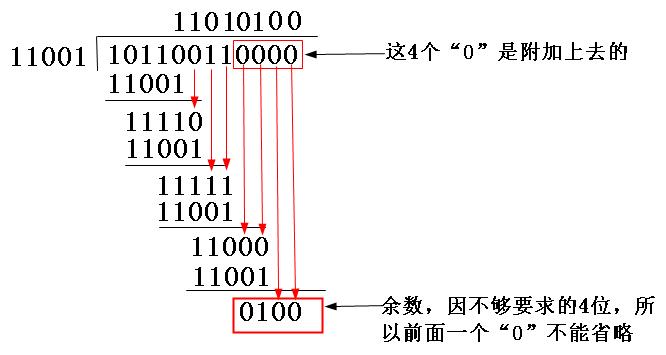
(2)因为生成多项式的位数为5,根据前面的介绍,得知CRC校验码的位数为4(校验码的位数比生成多项式的位数少1)。因为原数据帧10110011,在它后面再加4个0,得到101100110000,然后把这个数以“模2除法”方式除以生成多项式,得到的余数,即CRC校验码为0100,如图5-10所示。注意参考前面介绍的“模2除法”运算法则。
图5-10 CRC校验码计算示例
(3)把上步计算得到的CRC校验码0100替换原始帧101100110000后面的四个“0”,得到新帧101100110100。再把这个新帧发送到接收端。
(4)当以上新帧到达接收端后,接收端会把这个新帧再用上面选定的除数11001以“模2除法”方式去除,验证余数是否为0,如果为0,则证明该帧数据在传输过程中没有出现差错,否则出现了差错。
通过以上CRC校验原理的剖析和CRC校验码的计算示例的介绍,大家应该对这种看似很复杂的CRC校验原理和计算方法应该比较清楚了。
下面大家做一个练习,假设CRC生成多项式为G(X) = X5 + X4 +X+1,要发送的二进制序列为100101110,求CRC校验码是多少。
2.CRC-12 源代码
准备工作: CRC-12生成多项式 x12+x3+x2+x+1; 对应 0x180F;
代码:
package CRC;
public class CRC12 {
public static String resultBinaryCRC=null; //crc用二进制表示
public static String messageBinary=null; //结果用二进制表示
public static String messageOct=null; //结果用十进制表示
public static int a = 0x180f; // 生成多项式
public static int CRCBIT = 12;
public static void main(String [] args){
String message="2";
CRC12 a=new CRC12();
a.doCalculate(message);
}
public void doCalculate(String Num)
{
String crcTemp = null;//余数
Boolean flag = true;
int number = Integer.valueOf(Num); // 发送的数据的十进制表示
int nextNumber = number << CRCBIT; // 变成了被除数
int NumberMinus = Integer.toBinaryString(nextNumber).length()- Integer.toBinaryString(a).length();// 找出被除数比除数多几个0
int nextNumberString12 = nextNumber >> NumberMinus; // 得到前13位的数值
// 前13位与除数做异或运算
while (NumberMinus >=0)
{
if (flag == true) //设置boolean目的是保证只运行一次代码
{
crcTemp = Integer.toBinaryString(nextNumberString12);
flag = false;
}
if (crcTemp.length() == 13) //余数补0,直到凑齐13位,然后再与生成多项式模2运算
{
nextNumberString12 = Integer.parseInt(crcTemp, 2) ^ a; // 余数与生成多项式异或运算
crcTemp = Integer.toBinaryString(nextNumberString12); // 将余数变成二进制表示
}
if(NumberMinus>0)
{crcTemp = crcTemp + "0";}
NumberMinus--;
}
int k=12-crcTemp.length(); //根据余数的位数,补0变成12位
StringBuilder resultCrc=new StringBuilder(); //创建最终结果的StringBuilder
resultCrc.append(Integer.toBinaryString(Integer.parseInt(Num)));
for(int i=0;i<k;i++) //余数不足12位,要补前导0,补齐12位
{
resultCrc.append("0");
}
resultCrc.append(crcTemp);
setMessageBinary(resultCrc.toString());
setResultBinaryCRC(crcTemp);
int temp=Integer.parseInt(messageBinary,2); //二进制变成十进制表示
String aaa=Integer.toHexString(temp);
setMessageOct(aaa);
System.out.println("你发送的数据十进制表示"+Num);
System.out.println("你发送的数据二进制表示"+Integer.toBinaryString(number));
System.out.println("校验码"+this.getResultBinaryCRC());
System.out.println("最终发送数据二进制表示是"+this.getMessageBinary());
System.out.println("最终发送数据十进制表示是"+this.getMessageOct());
}
public String getResultBinaryCRC() {
return resultBinaryCRC;
}
public void setResultBinaryCRC(String resultBinaryCRC) {
CRC12.resultBinaryCRC = resultBinaryCRC;
}
public String getMessageBinary() {
return messageBinary;
}
public void setMessageBinary(String messageBinary) {
CRC12.messageBinary = messageBinary;
}
public String getMessageOct() {
return messageOct;
}
public void setMessageOct(String messageOct) {
CRC12.messageOct = messageOct;
}
}






相关推荐
堆排序详细图解(通俗易懂)+排序算法----堆排序(超详细)堆排序详细图解(通俗易懂)+排序算法----堆排序(超详细)堆排序详细图解(通俗易懂)+排序算法----堆排序(超详细)堆排序详细图解(通俗易懂)+排序算法...
通过这个"通俗易懂版"的学习资源,你将能够深入理解每种设计模式的原理,掌握如何在实际项目中应用它们,提升代码的可维护性和复用性。阅读《设计模式_20090916.pdf》文档,结合具体的代码示例,相信你将能够更好地...
本篇将通俗易懂地介绍几种常见的设计模式,并提供相关的Java代码示例。 首先,设计模式主要分为三大类:创建模式、结构模式和行为模式。 **创建模式**关注的是对象的创建。例如: 1. **工厂模式**(Factory ...
本资源“通俗易懂的Java设计模式”旨在帮助初学者和有一定经验的开发者更好地理解和应用这些模式。 首先,设计模式的基本分类包括创建型、结构型和行为型三大类。创建型设计模式如单例(Singleton)、工厂方法...
非常好的通俗易懂的开关电源原理与维修12.zip
很详细 又不啰嗦的 ppt教程 通俗易懂不啰嗦
### 通俗易懂的Java IO讲解 在Java中,输入输出流(IO)是一个非常重要的概念,它涉及到了数据如何从一个地方传输到另一个地方。本文将深入浅出地介绍Java IO的基础概念,并通过实例帮助读者更好地理解这些概念。 ...
个人在学习ORACLE过程当中记录下来的学习笔记,通俗易懂,适合想快速了解ORACLE基本语法的朋友
### Delta-Sigma调制原理详解 #### 一、Delta-Sigma调制概述 Delta-Sigma (ΔΣ) 调制技术是一种广泛应用于模数转换器(ADC)和数模转换器(DAC)的设计方法。它以其简单的硬件实现、优秀的线性度以及出色的信噪比性能...
Language Integrated Query 是C#的一个强大特性,允许在代码中直接编写查询,支持对各种数据源(如数据库、集合等)进行操作。 7. **异步编程** 引入了async和await关键字,使得开发者能轻松编写非阻塞式的异步...
最全面的搜索引擎技术,含源代码,通俗易懂
本文通过通俗易懂的语言介绍了ARM中断处理的基本原理及其特有的中断嵌套概念。通过了解中断信号如何被处理器识别、处理,以及中断控制器如何管理多个中断源,读者可以更好地理解ARM架构下的中断机制,并为开发基于...
信捷PLC上位机源代码例子,modbusTCP通信,通俗易懂,C#源代码。
这是2009年5月份编辑完毕的一个高清PDF,采用通俗易懂的代码例子,揭开设计模式的神秘面纱。 1)如果您是一个代码的初学者,通过本书。您就明白什么事一段优秀的代码。 2)如果您是一个代码高手,通过本书,您将更...
java的资源。里面有很通俗易懂,容易入学入门的课件;一些上机题,一份考试题模板
单片机原理与应用是电子工程领域中的基础知识,尤其对于初学者来说,理解单片机的工作原理和操作方法至关重要。本教程旨在为初学者提供一个简单易懂的单片机学习平台,帮助他们轻松入门。教程作者以自身的学习经验为...
在编译阶段,Java源代码文件(.java)被编译成字节码文件(.class),这些字节码文件由JVM解释执行。Java环境变量配置包括设置JAVA-HOME环境变量,指向JDK的安装目录,以及配置Path和ClassPath环境变量,以便操作...
信捷PLC上位机Modbus TCP通信C#源代码实例,易懂教程,信捷PLC上位机Modbus TCP通信C#源代码实例,入门级的通俗易懂范例,信捷PLC上位机源代码例子,modbusTCP通信,通俗易懂,C#源代码。 ,信捷PLC; 上位机; modbus...
信捷PLC上位机Modbus TCP通信C#源代码实例解析,信捷PLC上位机源代码例子,modbusTCP通信,通俗易懂,C#源代码。 ,核心关键词:信捷PLC上位机源代码例子; modbusTCP通信; 通俗易懂; C#源代码;,"信捷PLC通信:Modbus ...
计算机组成原理是计算机科学与技术领域的一门基础课程,它主要研究计算机系统中硬件部分的结构、工作原理以及数据在计算机内部的表示和处理方式。本PPT课件旨在为初学者提供一个清晰易懂的学习路径,帮助理解复杂的...