Breadth-First Search Traversal Algorithm

Breadth-first search is a way to find all the vertices reachable from the a given source vertex, s. Like depth first search, BFS traverse a connected component of a given graph and defines a spanning tree. Intuitively, the basic idea of the breath-first search is this: send a wave out from source s. The wave hits all vertices 1 edge from s. From there, the wave hits all vertices 2 edges from s. Etc. We use FIFO queue Q to maintain the wavefront: v is in Q if and only if wave has hit v but has not come out of v yet.

 

Overall Strategy of BFS Algorithm

Breadth-first search starts at a given vertex s, which is at level 0. In the first stage, we visit all the vertices that are at the distance of one edge away. When we visit there, we paint as "visited," the vertices adjacent to the start vertex s - these vertices are placed into level 1. In the second stage, we visit all the new vertices we can reach at the distance of two edges away from the source vertex s. These new vertices, which are adjacent to level 1 vertices and not previously assigned to a level, are placed into level 2, and so on. The BFS traversal terminates when every vertex has been visited.

To keep track of progress, breadth-first-search colors each vertex. Each vertex of the graph is in one of three states:

1. Undiscovered;
2. Discovered but not fully explored; and
3. Fully explored.

The state of a vertex, u, is stored in a color variable as follows:

1. color[u] = White - for the "undiscovered" state,
2. color [u] = Gray - for the "discovered but not fully explored" state, and
3. color [u] = Black - for the "fully explored" state.

The BFS(G, s) algorithm develops a breadth-first search tree with the source vertex, s, as its root. The parent or predecessor of any other vertex in the tree is the vertex from which it was first discovered. For each vertex, v, the parent of v is placed in the variable π[v]. Another variable, d[v], computed by BFS contains the number of tree edges on the path from s to v. The breadth-first search uses a FIFO queue, Q, to store gray vertices.

 

Algorithm: Breadth-First Search Traversal

BFS(V, E, s)

1.         for each u in V − {s}             ▷ for each vertex u in V[G] except s.
2.             do color[u] ← WHITE
3.                 d[u] ← infinity
4.                 π[u] ← NIL
5.         color[s] ← GRAY                 ▷ Source vertex discovered
6.         d[s] ← 0                               ▷ initialize
7.         π[s] ← NIL                           ▷ initialize
8.         Q ← {}                                ▷ Clear queue Q
9.         ENQUEUE(Q, s)
10        while Q is non-empty
11.             do u ← DEQUEUE(Q)                      ▷ That is, u = head[Q]
12.                 for each v adjacent to u                  ▷ for loop for every node along with edge.
13.                         do if color[v] ← WHITE        ▷ if color is white you've never seen it before
14.                                 then  color[v] ← GRAY
15.                                          d[v] ← d[u] + 1
16.                                          π[v] ← u
17.                                          ENQUEUE(Q, v)
18.                 DEQUEUE(Q)
19.         color[u] ← BLACK

 

 

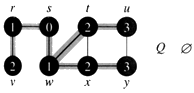
Example: The following figure (from CLRS) illustrates the progress of breadth-first search on the undirected sample graph.

a. After initialization (paint every vertex white, set d[u] to infinity for each vertex u,  and set the parent of every vertex to be NIL), the source vertex is discovered in line 5. Lines 8-9 initialize Q to contain just the source vertex s.

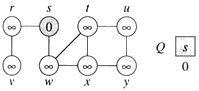
b. The algorithm discovers all vertices 1 edge from s i.e., discovered all vertices (w and r) at level 1.

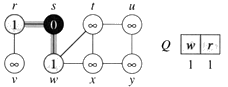
c.

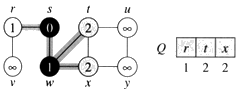
d. The algorithm discovers all vertices 2 edges from s i.e., discovered all vertices (t, x, and v) at level 2.

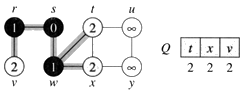
e.

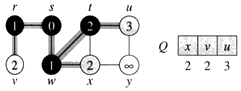
f.

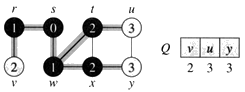
g. The algorithm discovers all vertices 3 edges from s i.e., discovered all vertices (u and y) at level 3.

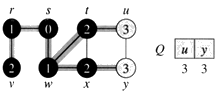
h.

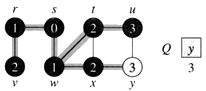
i. The algorithm terminates when every vertex has been fully explored.

 

Analysis

• The while-loop in breadth-first search is executed at most |V| times. The reason is that every vertex enqueued at most once. So, we have O(V).

• The for-loop inside the while-loop is executed at most |E| times if G is a directed graph or 2|E| times if G is undirected. The reason is that every vertex dequeued at most once and we examine (u, v) only when u is dequeued. Therefore, every edge examined at most once if directed, at most twice if undirected. So, we have O(E).

Therefore, the total running time for breadth-first search traversal is O(V + E).

 

Lemma 22.3 (CLRS)    At any time during the execution of BFS suppose that Q contains the vertices {v₁, v₂, ..., v_r} with v₁ at the head and v_r at the tail. Then d[v₁] ≤ d[v₂] ≤ ... ≤ d[v_r] ≤ d[v₁] + 1.

Let v be any vertex in V[G].  If v is reachable from s then let δ(s, v) be the minimum number of edges in E[G] that must be traversed to go from vertex s to vertex v. If v is not reachable from s then let δ(s, v) = ∞.

Theorem 22.5 (CLRS)    If BFS is run on graph G from a source vertex s in V[G] then for all v in V[G], d[v] = δ(s, v) and if v ≠ s is reachable from sthen one of the shortest paths from s to v is a shortest path from s to π[v] followed by the edge from π[v] to v.

BFS builds a tree called a breadth-first-tree containing all vertices reachable from s. The set of edges in the tree (called tree edges) contain (π[v], v) for all v where π[v] ≠ NIL.

If v is reachable from s then there is a unique path of tree edges from s to v. Print-Path(G, s, v) prints the vertices along that path in O(|V|) time.

Print-Path(G, s, v)

if v = s
        then print s
        else   if π[v] ← NIL
                then  print "no path exists from " s "to" v"
                else   Print-Path(G, s, π[v])
                        print v

 

Algorithms based on BFS

Based upon the BFS, there are O(V + E)-time algorithms for the following problems:

• Testing whether graph is connected.

• Computing a spanning forest of graph.

• Computing, for every vertex in graph, a path with the minimum number of edges between start vertex and current vertex or reporting that no such path exists.

• Computing a cycle in graph or reporting that no such cycle exists.

 

In our course, we will use BFS in the following:

• Prim's MST algorithm. (CLRS, Chapter 23.)

• Dijkstra's single source shortest path algorithm. (CLRS, Chapter 24.)

 

 

Some Applications of BFS

 

1. Bipartite Graph

We define bipartite graph as follows: A bipartite graph is an undirected graph G = (V, E) in which V can be partitioned into two sets V₁ and V₂such that (u, v) E implies either u in V₁ and v in V₂ or u in V₂ and v in V₁. That is, all edges go between the two sets V₁ and V₂.
In other to determine if a graph G = (V, E) is bipartite, we perform a BFS on it with a little modification such that whenever the BFS is at a vertexu and encounters a vertex v that is already 'gray' our modified BSF should check to see if the depth of both u and v are even, or if they are both odd. If either of these conditions holds which implies d[u] and d[v] have the same parity, then the graph is not bipartite. Note that this modification does not change the running time of BFS and remains O(V + E).
Formally, to check if the given graph is bipartite, the algorithm traverse the graph labeling the vertices 0, 1, or 2 corresponding to unvisited, partition 1 and partition 2 nodes. If an edge is detected between two vertices in the same partition, the algorithm returns.

 

ALGORITHM: BIPARTITE (G, S)

For each vertex u in V[G] − {s}
   do color[u] ← WHITE
        d[u] ← ∞
        partition[u] ← 0
color[s] ← GRAY
partition[s] ← 1
d[s] ← 0
Q ← [s]
while Queue 'Q' is non-empty
      do u ← head [Q]
         for each v in Adj[u] do
                if partition [u] ← partition [v]
                   then   return 0
                 else
                       if color[v] ← WHITE then
                            then color[v] ← gray
                                   d[v] = d[u] + 1
                                   partition[v] ← 3 − partition[u]
                                   ENQUEUE (Q, v)
           DEQUEUE (Q)
Color[u] ← BLACK
Return 1

Correctness

As Bipartite (G, S) traverse the graph it labels the vertices with a partition number consisted with the graph being bipartite. If at any vertex, algorithm detects an inconsistency, it shows with an invalid return value. Partition value of u will always be a valid number as it was enqueued at some point and its partition was assigned at that point. At line 19, partition of v will unchanged if it already set, otherwise it will be set to a value opposite to that of vertex u.

Analysis

The lines added to BFS algorithm take constant time to execute and so the running time is the same as that of BFS which is O(V + E).

 

2. Diameter of Tree

The diameter of a tree T = (V, E) is the largest of all shortest-path distance in the tree and given by max[dist(u, v)]. As we have mentioned that BSF can be use to compute, for every vertex in graph, a path with the minimum number of edges between start vertex and current vertex. It is quite easy to compute the diameter of a tree. For each vertex in the tree, we use BFS algorithm to get a shortest-path. By using a global variable length, we record the largest of all shortest-paths.

ALGORITHM: TREE_DIAMETER (T)

maxlength ← 0
for s ← 0 to s < |V[T]|
      do temp ← BSF(T, S)
            if maxlength < temp
                   maxlength ← temp
                   increment s by 1
return maxlength

 

Analysis

This will clearly takes O(V(V + E)) time.

 

From: http://www.personal.kent.edu/~rmuhamma/Algorithms/MyAlgorithms/GraphAlgor/breadthSearch.htm