信息论中的熵借鉴与物理学里的概念,物理学里熵来自于热力学第二定律,描述了功与热的转化,公式上是温度(不是温度变化值)除热量变化值所得的商,标志热量转化为功的程度,物质微观热运动时,混乱程度的标志。看得出来在封闭的系统中是一个熵是增加的。
熵是混乱和无序的度量 。熵值越大,混乱无序的程度越大。生命是高度的有序,智慧是高度的有序,局部的有序是可能的,但必须以其他地方的更大无序为代价,生命和智慧算作负熵。更多详细的内容,百度百科 上说的挺不错的。
信息论首先定义信息就是消除不确定性的东西,一系列的概念及所能表现的性质相当完备和一致,不得不佩服这些开创者的洞察力和跨域的综合能力。
任意随机事件的自信息量定义为该事件发生概率的对数的负值。设I(xi)=-log p(xi) 事件xi 的概率为p(xi),对于离散符号集合,定义熵为
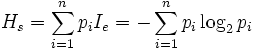
首先,熵值是对应于一个系统或符号集合而言,并不是求对一个符号的熵,当所有的符号出现概率相同的时候,对应的熵值最大,因为我们对下一个将出现什么符号的不确定程度越大。
对于离散随机变量x和任意函数f, 我们有H(f(x))<=H(x),即对原始信号的任何处理都不能增加熵(也就是信息量)。另外,任意改变事件的标记,不会影响这组符号的熵,因为熵只与每个符号的出现概率有关,而与符号本身无关。
我们记P(f(x))为f(x)出现的概率,那么H(f(x))= E[log1/p(f(x))], H(x) = E[log1/p(x)];
其中p(f(x))>= p(x),f(x)的离散值数目<=x,所以H(f(x)) <= H(x).
而对于连续的随机变量的情况,上述不一定成立,因为f(x)后的积分值很可能会发生变化,所以最后的熵值往往是不同的,因为f(x)与x是一一对应的,如果因此而说f(x)和x具有不同的内在无序性是没有意义的,除非加入某些随机性后,比如函数映射时随机改变映射之间的位置。
实际应用中,相对熵和熵之间的差值对我们来说更加重要。
相对熵,用经常使用的比值来定义
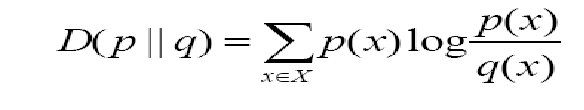 ,还有一个形式是E q(x)log q(x)/p(x).
,还有一个形式是E q(x)log q(x)/p(x).
那么交叉熵就是H(X, q) = H(X) + D(p||q) = - E p(x) log q(x), 其中X~p(x), q(X)用于近似p(x)的概率分布,它的概念用来衡量估值模型与真实概率分布间差异情况。
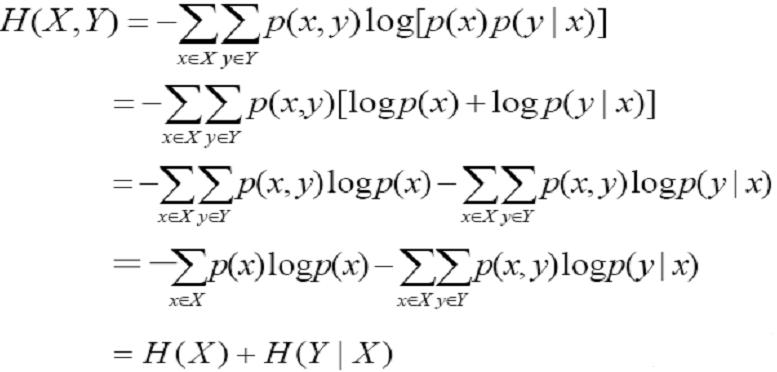
这时候互传信息量为 I(X;Y) = H(X) - H(X|Y),展开式子又可得下式。
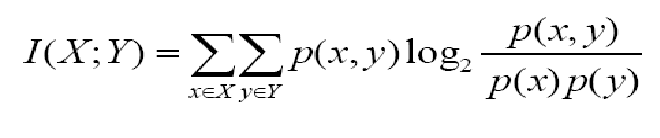
可以认为它就是联合概率分布与各自概率乘积之间的相对熵,衡量的是x,y的分布于统计独立的差别程度。
注意上面的交叉熵和互传信息量都不服从全部度量性质,联合熵总是比单独的熵要大,显然不确定性越大。
-----------------------
后记一些关于熵的内容(Added at 2009-09-28)
热力学第二定律是一个经验公式,当前还没有观察到违反它的现象发生。熵的概念最早来自描述能量在空间中分布的均匀程度,能量分布得越均匀,熵就越大,当然其过程来自于对热力学过程的研究。
虽然热力学第一定律描述能量守恒,但第二定律表明内能不如机械能,电能好用,它只能部分用于做功,表明能量的品质是在降级,这就是能量的耗散与退化。熵就被引入来描述能量耗散过程。
比较不均匀的状态是比较有序的状态,从微观的角度来讲,热传递过程也是从比较有序的状态变成比较无序的状态,例如,温度高的物体说明其分子运动比较剧烈,这是一种秩序,达到热平衡后两者温度一致,热运动没有区别了,变成无序。所以说熵是表征系统无序程度的物理量。
熵作为一个数学物理量,当然有正负之分,只不过在孤立系统中其总是大于等于0,特别是物理上。例如生命就可以说是靠负熵维持的。顺带附上一片有趣的日志,别人理解描述的深刻的多。
http://buguang.spaces.live.com/blog/cns!846EA6D78FBE7773!1330.entry
分享到:






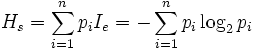
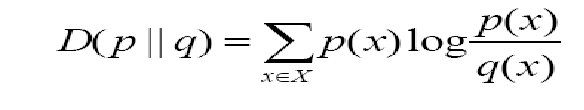 ,还有一个形式是E q(x)log q(x)/p(x).
,还有一个形式是E q(x)log q(x)/p(x).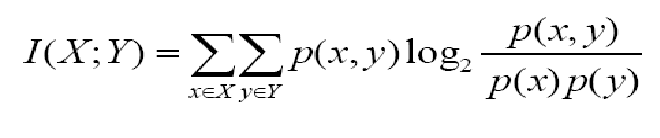



相关推荐
信息熵则衡量了信息的不确定性,可以反映课堂活动的多样性和复杂性。类别频度图、互动曲线和迁移矩阵则是Flanders分析的可视化工具,能清晰展示不同行为的出现频率和模式。 S-T分析,即时间序列分析,是一种追踪和...
在决策树算法中,我们需要计算决策属性的信息熵和条件属性的信息增益,然后选择具有最大信息增益的属性作为当前节点的测试属性。 六、朴素贝叶斯分类 朴素贝叶斯分类是指使用贝叶斯定理来分类数据的过程。在朴素...
信息熵越小,表示数据集分类的确定性越高,信息增益越大,表明该特征对分类的贡献越大。 3. **数据集与特征**:实验选择了是否打网球的数据集,包含14组记录,通过天气、气温、湿度和风这四个属性进行分类。每个...
- Flanders分析:这是一种分析课堂互动的方法,计算信息熵,理解信息传递的效率。 - 类别频度图和迁移矩阵:绘制这些图形来可视化不同行为的频率和转换关系。 - S-T分析:分析教学过程中的时间序列变化,画出S-T...
1. **回归分析**:如逻辑回归(Logistic Regression)用于二分类问题,决策树(如ID3算法)则通过信息熵选择最佳属性进行划分,人工神经网络(如BP神经网络)则模拟人脑神经元结构进行复杂问题建模。 2. **模型评价...
- **信息论**:讲解信息熵、互信息、条件熵等概念,它们在衡量数据的不确定性以及选择模型复杂度时起着重要作用。 - **核方法**:如高斯核(RBF)、多项式核等,这些是支持向量机和其他非线性分类器的核心。 - **...
它通过信息熵和信息增益来选择最佳分割属性,递归地划分数据空间,最终形成易于理解的决策规则。 3. Naive Bayes算法:这是一种基于贝叶斯定理的简单但强大的分类算法,假设各特征之间相互独立。在文本分类和垃圾...
### C++特征工程学习笔记 #### 1. 特征工程概述 特征工程(Feature Engineering)是机器学习项目中至关重要的一步,它涉及到从原始数据中选择、转换和创建特征,目的是为了使这些特征能够更好地匹配机器学习算法,...
信息熵是衡量数据集纯度的一个指标,而信息增益则是指选择某个属性后数据集纯度的提升程度。构建决策树时,从根节点开始,逐步选择信息增益最大的属性作为划分标准,直到满足停止条件。决策树模型易于解释,能够处理...
这些笔记可能包括决策树的构造过程、剪枝策略、信息熵和信息增益的计算、以及如何处理连续值和缺失值等问题。 C#标签表明这部分内容可能是用C#编程语言实现C4.5算法的讲解或示例代码。C#是一种面向对象的编程语言,...
8. **熵编码**:包括特征提起和量化,是无损压缩的一种,旨在根据数据的统计特性减少信息熵,降低数据冗余。 9. **图像编码的子图像块大小**:通常使用8x8的M×M块,便于处理和压缩。 10. **霍夫曼编码**:一种变...
我所了解的有关人工智能/数据科学/机器学习/统计建模/模式识别/您想要称呼本笔记内容的一切。 所有这些之间的界线都非常模糊,但是它们都试图回答相同的问题:“我们如何从数据中学习?” 机器学习基本上只是花哨的...