LeetCode 78 - Subsets

Given a set of distinct integers, S, return all possible subsets.

Note:

• Elements in a subset must be in non-descending order.
• The solution set must not contain duplicate subsets.

For example,
If S = [1,2,3], a solution is:

[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

 

其实就是Power Set.

Solution 1:

DFS, Recursive

public List<List<Integer>> subsets(int[] S) {
    List<List<Integer>> result = new ArrayList<>();
    Arrays.sort(S);
    getSubsets(result, new ArrayList<Integer>(), S, 0);
    return result;
}
private void getSubsets(List<List<Integer>> result, List<Integer> list, int[] S, int start) {
    result.add(new ArrayList<Integer>(list));
    for(int i=start; i<S.length; i++) {
        list.add(S[i]);
        getSubsets(result, list, S, i+1);
        list.remove(list.size()-1);
    }
}

 

vector<vector<int>> subsets(vector<int>& nums) {
    vector<vector<int>> res;
    vector<int> list;
    sort(nums.begin(), nums.end());
    function<void(int)> backtrack = [&](int start) {
        res.push_back(list);
        for(int i=start; i<nums.size(); i++) {
            list.push_back(nums[i]);
            backtrack(i+1);
            list.pop_back();
        }
    };
    backtrack(0);
    return res;
}

 

Solution 2:

BFS, Iterative.

public List<List<Integer>> subsets(int[] S) {
    List<List<Integer>> result = new ArrayList<>();
    Arrays.sort(S);
    result.add(new ArrayList<Integer>());
    for(int item: S) {
        List<List<Integer>> newResult = new ArrayList<>(result);
        for(List<Integer> list: result) {
            List<Integer> newList = new ArrayList<>(list);
            newList.add(item);
            newResult.add(newList);
        }
        result = newResult;
    }
    return result;
}

Output:

[[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]] 

vector<vector<int>> subsets(vector<int>& nums) {
    vector<vector<int>> res;
    res.push_back(vector<int>());
    sort(nums.begin(), nums.end());
    for(int num:nums) {
        int n = res.size();
        for(int i=0; i<n; i++) {
            auto list = res[i];
            list.push_back(num);
            res.push_back(list);
        }
    }
    return res;
}

 

Solution 3:

Bitmap, binary representation

In S, 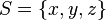, a 1 in the position corresponding to the location in the set indicates the presence of the element. So {x, y} = 110.

For the whole power set of S we get:

• { } = 000 (Binary) = 0 (Decimal)
• {x} = 100 = 4
• {y} = 010 = 2
• {z} = 001 = 1
• {x, y} = 110 = 6
• {x, z} = 101 = 5
• {y, z} = 011 = 3
• {x, y, z} = 111 = 7

public List<List<Integer>> subsets(int[] S) {
    List<List<Integer>> result = new ArrayList<>();
    Arrays.sort(S);
    int n = S.length;
    int size = (int)Math.pow(2, n);
    for(int i=0; i<size; i++) {
        List<Integer> list = new ArrayList<>();
        for(int j=0; j<n; j++) {
            if((i>>>j & 1) == 1) {
                list.add(S[j]);
            }
        }
        result.add(list);
    }
    return result;
}

 

vector<vector<int>> subsets(vector<int>& nums) {
    int n = nums.size();
    int size = pow(2, n);
    sort(nums.begin(), nums.end());
    vector<vector<int>> res;
    for(int i=0; i<size; i++) {
        vector<int> v;
        for(int j=0; j<n; j++) {
            if(i&(1<<j)) v.push_back(nums[j]);
        }
        res.push_back(v);
    }
    return res;
}

    

Time Complexity: O(n2^n)

 

Reference:

http://rosettacode.org/wiki/Power_set#Java