From: http://cslibrary.stanford.edu/110/BinaryTrees.html

Binary Trees

by Nick Parlante

This article introduces the basic concepts of binary trees, and then works through a series of practice problems with solution code in C/C++ and Java. Binary trees have an elegant recursive pointer structure, so they are a good way to learn recursive pointer algorithms.

Contents

Section 1. Binary Tree Structure -- a quick introduction to binary trees and the code that operates on them 
Section 2. Binary Tree Problems -- practice problems in increasing order of difficulty 
Section 3. C Solutions -- solution code to the problems for C and C++ programmers 
Section 4. Java versions -- how binary trees work in Java, with solution code

Stanford CS Education Library -- #110

This is article #110 in the Stanford CS Education Library. This and other free CS materials are available at the library (http://cslibrary.stanford.edu/). That people seeking education should have the opportunity to find it. This article may be used, reproduced, excerpted, or sold so long as this paragraph is clearly reproduced. Copyright 2000-2001, Nick Parlante, [e-mail].

Related CSLibrary Articles

• Linked List Problems (http://cslibrary.stanford.edu/105/) -- a large collection of linked list problems using various pointer techniques (while this binary tree article concentrates on recursion)
• Pointer and Memory (http://cslibrary.stanford.edu/102/) -- basic concepts of pointers and memory
• The Great Tree-List Problem (http://cslibrary.stanford.edu/109/) -- a great pointer recursion problem that uses both trees and lists

Section 1 -- Introduction To Binary Trees

A binary tree is made of nodes, where each node contains a "left" pointer, a "right" pointer, and a data element. The "root" pointer points to the topmost node in the tree. The left and right pointers recursively point to smaller "subtrees" on either side. A null pointer represents a binary tree with no elements -- the empty tree. The formal recursive definition is: a binary tree is either empty (represented by a null pointer), or is made of a single node, where the left and right pointers (recursive definition ahead) each point to a binary tree. 
 

 
 

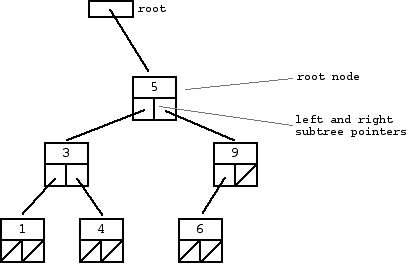
A "binary search tree" (BST) or "ordered binary tree" is a type of binary tree where the nodes are arranged in order: for each node, all elements in its left subtree are less-or-equal to the node (<=), and all the elements in its right subtree are greater than the node (>). The tree shown above is a binary search tree -- the "root" node is a 5, and its left subtree nodes (1, 3, 4) are <= 5, and its right subtree nodes (6, 9) are > 5. Recursively, each of the subtrees must also obey the binary search tree constraint: in the (1, 3, 4) subtree, the 3 is the root, the 1 <= 3 and 4 > 3. Watch out for the exact wording in the problems -- a "binary search tree" is different from a "binary tree".

The nodes at the bottom edge of the tree have empty subtrees and are called "leaf" nodes (1, 4, 6) while the others are "internal" nodes (3, 5, 9).

Binary Search Tree Niche

Basically, binary search trees are fast at insert and lookup. The next section presents the code for these two algorithms. On average, a binary search tree algorithm can locate a node in an N node tree in order lg(N) time (log base 2). Therefore, binary search trees are good for "dictionary" problems where the code inserts and looks up information indexed by some key. The lg(N) behavior is the average case -- it's possible for a particular tree to be much slower depending on its shape.

Strategy

Some of the problems in this article use plain binary trees, and some use binary search trees. In any case, the problems concentrate on the combination of pointers and recursion. (See the articles linked above for pointer articles that do not emphasize recursion.)

For each problem, there are two things to understand...

• The node/pointer structure that makes up the tree and the code that manipulates it
• The algorithm, typically recursive, that iterates over the tree

When thinking about a binary tree problem, it's often a good idea to draw a few little trees to think about the various cases.

Typical Binary Tree Code in C/C++

As an introduction, we'll look at the code for the two most basic binary search tree operations -- lookup() and insert(). The code here works for C or C++. Java programers can read the discussion here, and then look at the Java versions in Section 4.

In C or C++, the binary tree is built with a node type like this...

struct node { 
    int data; 
    struct node* left; 
    struct node* right; 
} 
 

Lookup()

Given a binary search tree and a "target" value, search the tree to see if it contains the target. The basic pattern of the lookup() code occurs in many recursive tree algorithms: deal with the base case where the tree is empty, deal with the current node, and then use recursion to deal with the subtrees. If the tree is a binary search tree, there is often some sort of less-than test on the node to decide if the recursion should go left or right.

/* 
 Given a binary tree, return true if a node 
 with the target data is found in the tree. Recurs 
 down the tree, chooses the left or right 
 branch by comparing the target to each node. 
*/ 
static int lookup(struct node* node, int target) { 
  // 1. Base case == empty tree 
  // in that case, the target is not found so return false 
  if (node == NULL) { 
    return(false); 
  } 
  else { 
    // 2. see if found here 
    if (target == node->data) return(true); 
    else { 
      // 3. otherwise recur down the correct subtree 
      if (target < node->data) return(lookup(node->left, target)); 
      else return(lookup(node->right, target)); 
    } 
  } 
} 
 

The lookup() algorithm could be written as a while-loop that iterates down the tree. Our version uses recursion to help prepare you for the problems below that require recursion.

Pointer Changing Code

There is a common problem with pointer intensive code: what if a function needs to change one of the pointer parameters passed to it? For example, the insert() function below may want to change the root pointer. In C and C++, one solution uses pointers-to-pointers (aka "reference parameters"). That's a fine technique, but here we will use the simpler technique that a function that wishes to change a pointer passed to it will return the new value of the pointer to the caller. The caller is responsible for using the new value. Suppose we have a change() function that may change the the root, then a call to change() will look like this...

// suppose the variable "root" points to the tree 
root = change(root);

We take the value returned by change(), and use it as the new value for root. This construct is a little awkward, but it avoids using reference parameters which confuse some C and C++ programmers, and Java does not have reference parameters at all. This allows us to focus on the recursion instead of the pointer mechanics. (For lots of problems that use reference parameters, see CSLibrary #105, Linked List Problems, http://cslibrary.stanford.edu/105/).

Insert()

Insert() -- given a binary search tree and a number, insert a new node with the given number into the tree in the correct place. The insert() code is similar to lookup(), but with the complication that it modifies the tree structure. As described above, insert() returns the new tree pointer to use to its caller. Calling insert() with the number 5 on this tree...

    2 
   / \ 
  1   10

returns the tree...

    2 
   / \ 
  1   10 
     / 
    5

The solution shown here introduces a newNode() helper function that builds a single node. The base-case/recursion structure is similar to the structure in lookup() -- each call checks for the NULL case, looks at the node at hand, and then recurs down the left or right subtree if needed.

/* 
 Helper function that allocates a new node 
 with the given data and NULL left and right 
 pointers. 
*/ 
struct node* NewNode(int data) { 
  struct node* node = new(struct node);    // "new" is like "malloc" 
  node->data = data; 
  node->left = NULL; 
  node->right = NULL;

  return(node); 
} 
 

/* 
 Give a binary search tree and a number, inserts a new node 
 with the given number in the correct place in the tree. 
 Returns the new root pointer which the caller should 
 then use (the standard trick to avoid using reference 
 parameters). 
*/ 
struct node* insert(struct node* node, int data) { 
  // 1. If the tree is empty, return a new, single node 
  if (node == NULL) { 
    return(newNode(data)); 
  } 
  else { 
    // 2. Otherwise, recur down the tree 
    if (data <= node->data) node->left = insert(node->left, data); 
    else node->right = insert(node->right, data);

    return(node); // return the (unchanged) node pointer 
  } 
} 
 

The shape of a binary tree depends very much on the order that the nodes are inserted. In particular, if the nodes are inserted in increasing order (1, 2, 3, 4), the tree nodes just grow to the right leading to a linked list shape where all the left pointers are NULL. A similar thing happens if the nodes are inserted in decreasing order (4, 3, 2, 1). The linked list shape defeats the lg(N) performance. We will not address that issue here, instead focusing on pointers and recursion.

Section 2 -- Binary Tree Problems

Here are 14 binary tree problems in increasing order of difficulty. Some of the problems operate on binary search trees (aka "ordered binary trees") while others work on plain binary trees with no special ordering. The next section, Section 3, shows the solution code in C/C++. Section 4 gives the background and solution code in Java. The basic structure and recursion of the solution code is the same in both languages -- the differences are superficial.

Reading about a data structure is a fine introduction, but at some point the only way to learn is to actually try to solve some problems starting with a blank sheet of paper. To get the most out of these problems, you should at least attempt to solve them before looking at the solution. Even if your solution is not quite right, you will be building up the right skills. With any pointer-based code, it's a good idea to make memory drawings of a a few simple cases to see how the algorithm should work.

1. build123()

This is a very basic problem with a little pointer manipulation. (You can skip this problem if you are already comfortable with pointers.) Write code that builds the following little 1-2-3 binary search tree...

    2 
   / \ 
  1   3

Write the code in three different ways...

• a: by calling newNode() three times, and using three pointer variables
• b: by calling newNode() three times, and using only one pointer variable
• c: by calling insert() three times passing it the root pointer to build up the tree

(In Java, write a build123() method that operates on the receiver to change it to be the 1-2-3 tree with the given coding constraints. See Section 4.)

struct node* build123() { 
 

2. size()

This problem demonstrates simple binary tree traversal. Given a binary tree, count the number of nodes in the tree.

int size(struct node* node) { 
 

3. maxDepth()

Given a binary tree, compute its "maxDepth" -- the number of nodes along the longest path from the root node down to the farthest leaf node. The maxDepth of the empty tree is 0, the maxDepth of the tree on the first page is 3.

int maxDepth(struct node* node) { 
 

4. minValue()

Given a non-empty binary search tree (an ordered binary tree), return the minimum data value found in that tree. Note that it is not necessary to search the entire tree. A maxValue() function is structurally very similar to this function. This can be solved with recursion or with a simple while loop.

int minValue(struct node* node) { 
 

5. printTree()

Given a binary search tree (aka an "ordered binary tree"), iterate over the nodes to print them out in increasing order. So the tree...

       4 
      / \ 
     2   5 
    / \ 
   1   3

Produces the output "1 2 3 4 5". This is known as an "inorder" traversal of the tree.

Hint: For each node, the strategy is: recur left, print the node data, recur right.

void printTree(struct node* node) { 
 

6. printPostorder()

Given a binary tree, print out the nodes of the tree according to a bottom-up "postorder" traversal -- both subtrees of a node are printed out completely before the node itself is printed, and each left subtree is printed before the right subtree. So the tree...

       4 
      / \ 
     2   5 
    / \ 
   1   3

Produces the output "1 3 2 5 4". The description is complex, but the code is simple. This is the sort of  bottom-up traversal that would be used, for example, to evaluate an expression tree where a node is an operation like '+' and its subtrees are, recursively, the two subexpressions for the '+'.

void printPostorder(struct node* node) { 
 

7. hasPathSum()

We'll define a "root-to-leaf path" to be a sequence of nodes in a tree starting with the root node and proceeding downward to a leaf (a node with no children). We'll say that an empty tree contains no root-to-leaf paths. So for example, the following tree has exactly four root-to-leaf paths:

              5 
             / \ 
            4   8 
           /   / \ 
          11  13  4 
         /  \      \ 
        7    2      1

Root-to-leaf paths: 
   path 1: 5 4 11 7 
   path 2: 5 4 11 2 
   path 3: 5 8 13 
   path 4: 5 8 4 1

For this problem, we will be concerned with the sum of the values of such a path -- for example, the sum of the values on the 5-4-11-7 path is 5 + 4 + 11 + 7 = 27.

Given a binary tree and a sum, return true if the tree has a root-to-leaf path such that adding up all the values along the path equals the given sum. Return false if no such path can be found. (Thanks to Owen Astrachan for suggesting this problem.)

int hasPathSum(struct node* node, int sum) { 
 

8. printPaths()

Given a binary tree, print out all of its root-to-leaf paths as defined above. This problem is a little harder than it looks, since the "path so far" needs to be communicated between the recursive calls. Hint: In C, C++, and Java, probably the best solution is to create a recursive helper function printPathsRecur(node, int path[], int pathLen), where the path array communicates the sequence of nodes that led up to the current call. Alternately, the problem may be solved bottom-up, with each node returning its list of paths. This strategy works quite nicely in Lisp, since it can exploit the built in list and mapping primitives. (Thanks to Matthias Felleisen for suggesting this problem.)

Given a binary tree, print out all of its root-to-leaf paths, one per line.

void printPaths(struct node* node) { 
 

9. mirror()

Change a tree so that the roles of the left and right pointers are swapped at every node.

 So the tree... 
       4 
      / \ 
     2   5 
    / \ 
   1   3

 is changed to... 
       4 
      / \ 
     5   2 
        / \ 
       3   1

The solution is short, but very recursive. As it happens, this can be accomplished without changing the root node pointer, so the return-the-new-root construct is not necessary. Alternately, if you do not want to change the tree nodes, you may construct and return a new mirror tree based on the original tree.

void mirror(struct node* node) { 
 

10. doubleTree()

For each node in a binary search tree, create a new duplicate node, and insert the duplicate as the left child of the original node. The resulting tree should still be a binary search tree.

 So the tree... 
    2 
   / \ 
  1   3

 is changed to... 
       2 
      / \ 
     2   3 
    /   / 
   1   3 
  / 
 1

As with the previous problem, this can be accomplished without changing the root node pointer.

void doubleTree(struct node* node) { 
 

11. sameTree()

Given two binary trees, return true if they are structurally identical -- they are made of nodes with the same values arranged in the same way. (Thanks to Julie Zelenski for suggesting this problem.)

int sameTree(struct node* a, struct node* b) { 
 

12. countTrees()

This is not a binary tree programming problem in the ordinary sense -- it's more of a math/combinatorics recursion problem that happens to use binary trees. (Thanks to Jerry Cain for suggesting this problem.)

Suppose you are building an N node binary search tree with the values 1..N. How many structurally different  binary search trees are there that store those values? Write a recursive function that, given the number of distinct values, computes the number of structurally unique binary search trees that store those values. For example, countTrees(4) should return 14, since there are 14  structurally unique binary search trees that store 1, 2, 3, and 4. The base case is easy, and the recursion is short but dense. Your code should not construct any actual trees; it's just a counting problem.

int countTrees(int numKeys) { 
  
 

Binary Search Tree Checking (for problems 13 and 14)

This background is used by the next two problems: Given a plain binary tree, examine the tree to determine if it meets the requirement to be a binary search tree. To be a binary search tree, for every node, all of the nodes in its left tree must be <= the node, and all of the nodes in its right subtree must be > the node. Consider the following four examples...

a.  5   -> TRUE 
   / \ 
  2   7 
 

b.  5   -> FALSE, because the 6 is not ok to the left of the 5 
   / \ 
  6   7 
 

c.   5  -> TRUE 
    / \ 
   2   7 
  / 
 1

d.   5  -> FALSE, the 6 is ok with the 2, but the 6 is not ok with the 5 
    / \ 
   2   7 
  / \ 
 1   6

For the first two cases, the right answer can be seen just by comparing each node to the two nodes immediately below it. However, the fourth case shows how checking the BST quality may depend on nodes which are several layers apart -- the 5 and the 6 in that case. 
 

13 isBST() -- version 1

Suppose you have helper functions minValue() and maxValue() that return the min or max int value from a non-empty tree (see problem 3 above). Write an isBST() function that returns true if a tree is a binary search tree and false otherwise. Use the helper functions, and don't forget to check every node in the tree. It's ok if your solution is not very efficient. (Thanks to Owen Astrachan for the idea of having this problem, and comparing it to problem 14)

Returns true if a binary tree is a binary search tree.

int isBST(struct node* node) { 
 

14. isBST() -- version 2

Version 1 above runs slowly since it traverses over some parts of the tree many times. A better solution looks at each node only once. The trick is to write a utility helper function isBSTRecur(struct node* node, int min, int max) that traverses down the tree keeping track of the narrowing min and max allowed values as it goes, looking at each node only once. The initial values for min and max should be INT_MIN and INT_MAX -- they narrow from there.

/* 
 Returns true if the given tree is a binary search tree 
 (efficient version). 
*/ 
int isBST2(struct node* node) { 
  return(isBSTRecur(node, INT_MIN, INT_MAX)); 
}

/* 
 Returns true if the given tree is a BST and its 
 values are >= min and <= max. 
*/ 
int isBSTRecur(struct node* node, int min, int max) { 
 

15. Tree-List

The Tree-List problem is one of the greatest recursive pointer problems ever devised, and it happens to use binary trees as well. CLibarary #109http://cslibrary.stanford.edu/109/  works through the Tree-List problem in detail and includes solution code in C and Java. The problem requires an understanding of binary trees, linked lists, recursion, and pointers. It's a great problem, but it's complex. 
  
 

Section 3 -- C/C++ Solutions

Make an attempt to solve each problem before looking at the solution -- it's the best way to learn.

1. Build123() Solution (C/C++)

// call newNode() three times 
struct node* build123a() { 
  struct node* root = newNode(2); 
  struct node* lChild = newNode(1); 
  struct node* rChild = newNode(3);

  root->left = lChild; 
  root->right= rChild;

  return(root); 
}

// call newNode() three times, and use only one local variable 
struct node* build123b() { 
  struct node* root = newNode(2); 
  root->left = newNode(1); 
  root->right = newNode(3);

  return(root); 
} 
 

/* 
 Build 123 by calling insert() three times. 
 Note that the '2' must be inserted first. 
*/ 
struct node* build123c() { 
  struct node* root = NULL; 
  root = insert(root, 2); 
  root = insert(root, 1); 
  root = insert(root, 3); 
  return(root); 
} 
 

2. size() Solution (C/C++)

/* 
 Compute the number of nodes in a tree. 
*/ 
int size(struct node* node) { 
  if (node==NULL) { 
    return(0); 
  } else { 
    return(size(node->left) + 1 + size(node->right)); 
  } 
} 
 

3. maxDepth() Solution (C/C++)

/* 
 Compute the "maxDepth" of a tree -- the number of nodes along 
 the longest path from the root node down to the farthest leaf node. 
*/ 
int maxDepth(struct node* node) { 
  if (node==NULL) { 
    return(0); 
  } 
  else { 
    // compute the depth of each subtree 
    int lDepth = maxDepth(node->left); 
    int rDepth = maxDepth(node->right);

    // use the larger one 
    if (lDepth > rDepth) return(lDepth+1); 
    else return(rDepth+1); 
  } 
} 
 

4. minValue() Solution (C/C++)

/* 
 Given a non-empty binary search tree, 
 return the minimum data value found in that tree. 
 Note that the entire tree does not need to be searched. 
*/ 
int minValue(struct node* node) { 
  struct node* current = node;

  // loop down to find the leftmost leaf 
  while (current->left != NULL) { 
    current = current->left; 
  }

  return(current->data); 
} 
 

5. printTree() Solution (C/C++)

/* 
 Given a binary search tree, print out 
 its data elements in increasing 
 sorted order. 
*/ 
void printTree(struct node* node) { 
  if (node == NULL) return;

  printTree(node->left); 
  printf("%d ", node->data); 
  printTree(node->right); 
} 
 

6. printPostorder() Solution (C/C++)

/* 
 Given a binary tree, print its 
 nodes according to the "bottom-up" 
 postorder traversal. 
*/ 
void printPostorder(struct node* node) { 
  if (node == NULL) return;

  // first recur on both subtrees 
  printTree(node->left); 
  printTree(node->right);

  // then deal with the node 
  printf("%d ", node->data); 
} 
 

7. hasPathSum() Solution (C/C++)

/* 
 Given a tree and a sum, return true if there is a path from the root 
 down to a leaf, such that adding up all the values along the path 
 equals the given sum.

 Strategy: subtract the node value from the sum when recurring down, 
 and check to see if the sum is 0 when you run out of tree. 
*/ 
int hasPathSum(struct node* node, int sum) { 
  // return true if we run out of tree and sum==0 
  if (node == NULL) { 
    return(sum == 0); 
  } 
  else { 
  // otherwise check both subtrees 
    int subSum = sum - node->data; 
    return(hasPathSum(node->left, subSum) || 
           hasPathSum(node->right, subSum)); 
  } 
} 
 

8. printPaths() Solution (C/C++)

/* 
 Given a binary tree, print out all of its root-to-leaf 
 paths, one per line. Uses a recursive helper to do the work. 
*/ 
void printPaths(struct node* node) { 
  int path[1000];

  printPathsRecur(node, path, 0); 
}

/* 
 Recursive helper function -- given a node, and an array containing 
 the path from the root node up to but not including this node, 
 print out all the root-leaf paths. 
*/ 
void printPathsRecur(struct node* node, int path[], int pathLen) { 
  if (node==NULL) return;

  // append this node to the path array 
  path[pathLen] = node->data; 
  pathLen++;

  // it's a leaf, so print the path that led to here 
  if (node->left==NULL && node->right==NULL) { 
    printArray(path, pathLen); 
  } 
  else { 
  // otherwise try both subtrees 
    printPathsRecur(node->left, path, pathLen); 
    printPathsRecur(node->right, path, pathLen); 
  } 
}

// Utility that prints out an array on a line. 
void printArray(int ints[], int len) { 
  int i; 
  for (i=0; i<len; i++) { 
    printf("%d ", ints[i]); 
  } 
  printf("\n"); 
} 
 

9. mirror() Solution (C/C++)

/* 
 Change a tree so that the roles of the 
 left and right pointers are swapped at every node.

 So the tree... 
       4 
      / \ 
     2   5 
    / \ 
   1   3

 is changed to... 
       4 
      / \ 
     5   2 
        / \ 
       3   1 
*/ 
void mirror(struct node* node) { 
  if (node==NULL) { 
    return; 
  } 
  else { 
    struct node* temp;

    // do the subtrees 
    mirror(node->left); 
    mirror(node->right);

    // swap the pointers in this node 
    temp = node->left; 
    node->left = node->right; 
    node->right = temp; 
  } 
} 
 

10. doubleTree() Solution (C/C++)

/* 
 For each node in a binary search tree, 
 create a new duplicate node, and insert 
 the duplicate as the left child of the original node. 
 The resulting tree should still be a binary search tree.

 So the tree... 
    2 
   / \ 
  1   3

 Is changed to... 
       2 
      / \ 
     2   3 
    /   / 
   1   3 
  / 
 1

*/ 
void doubleTree(struct node* node) { 
  struct node* oldLeft;

  if (node==NULL) return;

  // do the subtrees 
  doubleTree(node->left); 
  doubleTree(node->right);

  // duplicate this node to its left 
  oldLeft = node->left; 
  node->left = newNode(node->data); 
  node->left->left = oldLeft; 
} 
 

11. sameTree() Solution (C/C++)

/* 
 Given two trees, return true if they are 
 structurally identical. 
*/ 
int sameTree(struct node* a, struct node* b) { 
  // 1. both empty -> true 
  if (a==NULL && b==NULL) return(true);

  // 2. both non-empty -> compare them 
  else if (a!=NULL && b!=NULL) { 
    return( 
      a->data == b->data && 
      sameTree(a->left, b->left) && 
      sameTree(a->right, b->right) 
    ); 
  } 
  // 3. one empty, one not -> false 
  else return(false); 
} 
  
 

12. countTrees() Solution (C/C++)

/* 
 For the key values 1...numKeys, how many structurally unique 
 binary search trees are possible that store those keys.

 Strategy: consider that each value could be the root. 
 Recursively find the size of the left and right subtrees. 
*/ 
int countTrees(int numKeys) {

  if (numKeys <=1) { 
    return(1); 
  } 
  else { 
    // there will be one value at the root, with whatever remains 
    // on the left and right each forming their own subtrees. 
    // Iterate through all the values that could be the root... 
    int sum = 0; 
    int left, right, root;

    for (root=1; root<=numKeys; root++) { 
      left = countTrees(root - 1); 
      right = countTrees(numKeys - root);

      // number of possible trees with this root == left*right 
      sum += left*right; 
    }

    return(sum); 
  } 
} 
  
 

13. isBST1() Solution (C/C++)

/* 
 Returns true if a binary tree is a binary search tree. 
*/ 
int isBST(struct node* node) { 
  if (node==NULL) return(true);

  // false if the max of the left is > than us

  // (bug -- an earlier version had min/max backwards here) 
  if (node->left!=NULL && maxValue(node->left) > node->data) 
    return(false);

  // false if the min of the right is <= than us 
  if (node->right!=NULL && minValue(node->right) <= node->data) 
    return(false);

  // false if, recursively, the left or right is not a BST 
  if (!isBST(node->left) || !isBST(node->right)) 
    return(false);

  // passing all that, it's a BST 
  return(true); 
} 
  
 

14. isBST2() Solution (C/C++)

/* 
 Returns true if the given tree is a binary search tree 
 (efficient version). 
*/ 
int isBST2(struct node* node) { 
  return(isBSTUtil(node, INT_MIN, INT_MAX)); 
}

/* 
 Returns true if the given tree is a BST and its 
 values are >= min and <= max. 
*/ 
int isBSTUtil(struct node* node, int min, int max) { 
  if (node==NULL) return(true);

  // false if this node violates the min/max constraint 
  if (node->data<min || node->data>max) return(false);

  // otherwise check the subtrees recursively, 
  // tightening the min or max constraint 
  return 
    isBSTUtil(node->left, min, node->data) && 
    isBSTUtil(node->right, node->data+1, max) 
  ); 
} 
 

15. TreeList Solution (C/C++)

The solution code in C and Java to the great Tree-List recursion problem is in CSLibrary #109  http://cslibrary.stanford.edu/109/

Section 4 -- Java Binary Trees and Solutions

In Java, the key points in the recursion are exactly the same as in C or C++. In fact, I created the Java solutions by just copying the C solutions, and then making the syntactic changes. The recursion is the same, however the outer structure is slightly different.

In Java, we will have a BinaryTree object that contains a single root pointer. The root pointer points to an internal Node class that behaves just like the node struct in the C/C++ version. The Node class is private -- it is used only for internal storage inside the BinaryTree and is not exposed to clients. With this OOP structure, almost every operation has two methods: a one-line method on the BinaryTree that starts the computation, and a recursive method that works on the Node objects. For the lookup() operation, there is a BinaryTree.lookup() method that the client uses to start a lookup operation. Internal to the BinaryTree class, there is a private recursive lookup(Node) method that implements the recursion down the Node structure. This second, private recursive method is basically the same as the recursive C/C++ functions above -- it takes a Node argument and uses recursion to iterate over the pointer structure.

Java Binary Tree Structure

To get started, here are the basic definitions for the Java BinaryTree class, and the lookup() and insert() methods as examples...

// BinaryTree.java 
public class BinaryTree { 
  // Root node pointer. Will be null for an empty tree. 
  private Node root; 
 

  /* 
   --Node-- 
   The binary tree is built using this nested node class. 
   Each node stores one data element, and has left and right 
   sub-tree pointer which may be null. 
   The node is a "dumb" nested class -- we just use it for 
   storage; it does not have any methods. 
  */ 
  private static class Node { 
    Node left; 
    Node right; 
    int data;

    Node(int newData) { 
      left = null; 
      right = null; 
      data = newData; 
    } 
  }

  /** 
   Creates an empty binary tree -- a null root pointer. 
  */ 
  public void BinaryTree() { 
    root = null; 
  } 
 

  /** 
   Returns true if the given target is in the binary tree. 
   Uses a recursive helper. 
  */ 
  public boolean lookup(int data) { 
    return(lookup(root, data)); 
  } 
 

  /** 
   Recursive lookup  -- given a node, recur 
   down searching for the given data. 
  */ 
  private boolean lookup(Node node, int data) { 
    if (node==null) { 
      return(false); 
    }

    if (data==node.data) { 
      return(true); 
    } 
    else if (data<node.data) { 
      return(lookup(node.left, data)); 
    } 
    else { 
      return(lookup(node.right, data)); 
    } 
  } 
 

  /** 
   Inserts the given data into the binary tree. 
   Uses a recursive helper. 
  */ 
  public void insert(int data) { 
    root = insert(root, data); 
  } 
 

  /** 
   Recursive insert -- given a node pointer, recur down and 
   insert the given data into the tree. Returns the new 
   node pointer (the standard way to communicate 
   a changed pointer back to the caller). 
  */ 
  private Node insert(Node node, int data) { 
    if (node==null) { 
      node = new Node(data); 
    } 
    else { 
      if (data <= node.data) { 
        node.left = insert(node.left, data); 
      } 
      else { 
        node.right = insert(node.right, data); 
      } 
    }

    return(node); // in any case, return the new pointer to the caller 
  } 
 

OOP Style vs. Recursive Style

From the client point of view, the BinaryTree class demonstrates good OOP style -- it encapsulates the binary tree state, and the client sends messages like lookup() and insert() to operate on that state. Internally, the Node class and the recursive methods do not demonstrate OOP style. The recursive methods like insert(Node) and lookup (Node, int) basically look like recursive functions in any language. In particular, they do not operate against a "receiver" in any special way. Instead, the recursive methods operate on the arguments that are passed in which is the classical way to write recursion. My sense is that the OOP style and the recursive style do not be combined nicely for binary trees, so I have left them separate. Merging the two styles would be especially awkward for the "empty" tree (null) case, since you can't send a message to the null pointer. It's possible to get around that by having a special object to represent the null tree, but that seems like a distraction to me. I prefer to keep the recursive methods simple, and use different examples to teach OOP.

Java Solutions

Here are the Java solutions to the 14 binary tree problems. Most of the solutions use two methods:a one-line OOP method that starts the computation, and a recursive method that does the real operation. Make an attempt to solve each problem before looking at the solution -- it's the best way to learn.

1. Build123() Solution (Java)

/** 
 Build 123 using three pointer variables. 
*/ 
public void build123a() { 
  root = new Node(2); 
  Node lChild = new Node(1); 
  Node rChild = new Node(3);

  root.left = lChild; 
  root.right= rChild; 
}

/** 
 Build 123 using only one pointer variable. 
*/ 
public void build123b() { 
  root = new Node(2); 
  root.left = new Node(1); 
  root.right = new Node(3); 
} 
 

/** 
 Build 123 by calling insert() three times. 
 Note that the '2' must be inserted first. 
*/ 
public void build123c() { 
  root = null; 
  root = insert(root, 2); 
  root = insert(root, 1); 
  root = insert(root, 3); 
} 
 

2. size() Solution (Java)

/** 
 Returns the number of nodes in the tree. 
 Uses a recursive helper that recurs 
 down the tree and counts the nodes. 
*/ 
public int size() { 
  return(size(root)); 
}

private int size(Node node) { 
  if (node == null) return(0); 
  else { 
    return(size(node.left) + 1 + size(node.right)); 
  } 
} 
 

3. maxDepth() Solution (Java)

/** 
 Returns the max root-to-leaf depth of the tree. 
 Uses a recursive helper that recurs down to find 
 the max depth. 
*/ 
public int maxDepth() { 
  return(maxDepth(root)); 
}

private int maxDepth(Node node) { 
  if (node==null) { 
    return(0); 
  } 
  else { 
    int lDepth = maxDepth(node.left); 
    int rDepth = maxDepth(node.right);

    // use the larger + 1 
    return(Math.max(lDepth, rDepth) + 1); 
  } 
} 
 

4. minValue() Solution (Java)

/** 
 Returns the min value in a non-empty binary search tree. 
 Uses a helper method that iterates to the left to find 
 the min value. 
*/ 
public int minValue() { 
 return( minValue(root) ); 
} 
 

/** 
 Finds the min value in a non-empty binary search tree. 
*/ 
private int minValue(Node node) { 
  Node current = node; 
  while (current.left != null) { 
    current = current.left; 
  }

  return(current.data); 
}

5. printTree() Solution (Java)

/** 
 Prints the node values in the "inorder" order. 
 Uses a recursive helper to do the traversal. 
*/ 
public void printTree() { 
 printTree(root); 
 System.out.println(); 
}

private void printTree(Node node) { 
 if (node == null) return;

 // left, node itself, right 
 printTree(node.left); 
 System.out.print(node.data + "  "); 
 printTree(node.right); 
} 
 

6. printPostorder() Solution (Java)

/** 
 Prints the node values in the "postorder" order. 
 Uses a recursive helper to do the traversal. 
*/ 
public void printPostorder() { 
 printPostorder(root); 
 System.out.println(); 
}

public void printPostorder(Node node) { 
  if (node == null) return;

  // first recur on both subtrees 
  printPostorder(node.left); 
  printPostorder(node.right);

  // then deal with the node 
 System.out.print(node.data + "  "); 
} 
 

7. hasPathSum() Solution (Java)

/** 
 Given a tree and a sum, returns true if there is a path from the root 
 down to a leaf, such that adding up all the values along the path 
 equals the given sum.

 Strategy: subtract the node value from the sum when recurring down, 
 and check to see if the sum is 0 when you run out of tree. 
*/ 
public boolean hasPathSum(int sum) { 
 return( hasPathSum(root, sum) ); 
}

boolean hasPathSum(Node node, int sum) { 
  // return true if we run out of tree and sum==0 
  if (node == null) { 
    return(sum == 0); 
  } 
  else { 
  // otherwise check both subtrees 
    int subSum = sum - node.data; 
    return(hasPathSum(node.left, subSum) || hasPathSum(node.right, subSum)); 
  } 
} 
 

8. printPaths() Solution (Java)

/** 
 Given a binary tree, prints out all of its root-to-leaf 
 paths, one per line. Uses a recursive helper to do the work. 
*/ 
public void printPaths() { 
  int[] path = new int[1000]; 
  printPaths(root, path, 0); 
}

/** 
 Recursive printPaths helper -- given a node, and an array containing 
 the path from the root node up to but not including this node, 
 prints out all the root-leaf paths. 
*/ 
private void printPaths(Node node, int[] path, int pathLen) { 
  if (node==null) return;

  // append this node to the path array 
  path[pathLen] = node.data; 
  pathLen++;

  // it's a leaf, so print the path that led to here 
  if (node.left==null && node.right==null) { 
    printArray(path, pathLen); 
  } 
  else { 
  // otherwise try both subtrees 
    printPaths(node.left, path, pathLen); 
    printPaths(node.right, path, pathLen); 
  } 
}

/** 
 Utility that prints ints from an array on one line. 
*/ 
private void printArray(int[] ints, int len) { 
  int i; 
  for (i=0; i<len; i++) { 
   System.out.print(ints[i] + " "); 
  } 
  System.out.println(); 
} 
 

9. mirror() Solution (Java)

/** 
 Changes the tree into its mirror image.

 So the tree... 
       4 
      / \ 
     2   5 
    / \ 
   1   3

 is changed to... 
       4 
      / \ 
     5   2 
        / \ 
       3   1

 Uses a recursive helper that recurs over the tree, 
 swapping the left/right pointers. 
*/ 
public void mirror() { 
  mirror(root); 
}

private void mirror(Node node) { 
  if (node != null) { 
    // do the sub-trees 
    mirror(node.left); 
    mirror(node.right);

    // swap the left/right pointers 
    Node temp = node.left; 
    node.left = node.right; 
    node.right = temp; 
  } 
} 
 

10. doubleTree() Solution (Java)

/** 
 Changes the tree by inserting a duplicate node 
 on each nodes's .left. 
  
 

 So the tree... 
    2 
   / \ 
  1   3

 Is changed to... 
       2 
      / \ 
     2   3 
    /   / 
   1   3 
  / 
 1

 Uses a recursive helper to recur over the tree 
 and insert the duplicates. 
*/ 
public void doubleTree() { 
 doubleTree(root); 
}

private void doubleTree(Node node) { 
  Node oldLeft;

  if (node == null) return;

  // do the subtrees 
  doubleTree(node.left); 
  doubleTree(node.right);

  // duplicate this node to its left 
  oldLeft = node.left; 
  node.left = new Node(node.data); 
  node.left.left = oldLeft; 
} 
 

11. sameTree() Solution (Java)

/* 
 Compares the receiver to another tree to 
 see if they are structurally identical. 
*/ 
public boolean sameTree(BinaryTree other) { 
 return( sameTree(root, other.root) ); 
}

/** 
 Recursive helper -- recurs down two trees in parallel, 
 checking to see if they are identical. 
*/ 
boolean sameTree(Node a, Node b) { 
  // 1. both empty -> true 
  if (a==null && b==null) return(true);

  // 2. both non-empty -> compare them 
  else if (a!=null && b!=null) { 
    return( 
      a.data == b.data && 
      sameTree(a.left, b.left) && 
      sameTree(a.right, b.right) 
    ); 
  } 
  // 3. one empty, one not -> false 
  else return(false); 
} 
 

12. countTrees() Solution (Java)

/** 
 For the key values 1...numKeys, how many structurally unique 
 binary search trees are possible that store those keys?

 Strategy: consider that each value could be the root. 
 Recursively find the size of the left and right subtrees. 
*/ 
public static int countTrees(int numKeys) { 
  if (numKeys <=1) { 
    return(1); 
  } 
  else { 
    // there will be one value at the root, with whatever remains 
    // on the left and right each forming their own subtrees. 
    // Iterate through all the values that could be the root... 
    int sum = 0; 
    int left, right, root;

    for (root=1; root<=numKeys; root++) { 
      left = countTrees(root-1); 
      right = countTrees(numKeys - root);

      // number of possible trees with this root == left*right 
      sum += left*right; 
    }

    return(sum); 
  } 
} 
 

13. isBST1() Solution (Java)

/** 
 Tests if a tree meets the conditions to be a 
 binary search tree (BST). 
*/ 
public boolean isBST() { 
  return(isBST(root)); 
}

/** 
 Recursive helper -- checks if a tree is a BST 
 using minValue() and maxValue() (not efficient). 
*/ 
private boolean isBST(Node node) { 
  if (node==null) return(true);

  // do the subtrees contain values that do not 
  // agree with the node? 
  if (node.left!=null && maxValue(node.left) > node.data) return(false); 
  if (node.right!=null && minValue(node.right) <= node.data) return(false);

  // check that the subtrees themselves are ok 
  return( isBST(node.left) && isBST(node.right) ); 
} 
  
 

14. isBST2() Solution (Java)

/** 
 Tests if a tree meets the conditions to be a 
 binary search tree (BST). Uses the efficient 
 recursive helper. 
*/ 
public boolean isBST2() { 
 return( isBST2(root, Integer.MIN_VALUE, Integer.MAX_VALUE) ); 
}

/** 
  Efficient BST helper -- Given a node, and min and max values, 
  recurs down the tree to verify that it is a BST, and that all 
  its nodes are within the min..max range. Works in O(n) time -- 
  visits each node only once. 
*/ 
private boolean isBST2(Node node, int min, int max) { 
  if (node==null) { 
    return(true); 
  } 
  else { 
   // left should be in range  min...node.data 
    boolean leftOk = isBST2(node.left, min, node.data);

    // if the left is not ok, bail out 
    if (!leftOk) return(false);

    // right should be in range node.data+1..max 
    boolean rightOk = isBST2(node.right, node.data+1, max);

    return(rightOk); 
  } 
}