Reservoir Sampling - Choose K Numbers with Uniform Probability

Given that you receive one number at a time(streaming numbers), choose K numbers with uniform probability.

题目要求从n个input中random sample k个数 （k<=n)

其中n是未知的，input是以online的形式获得的。即给定一个function getInput(),
调用这个function每次可以获得一个数，取完为止，但是你不知道一共有多少个数。

要求：
1. 返回 k个数，保证randomness
2. 可用的memory只有k，即最多只能存k个数，所以不能把n个数都存下来，再random sample

 

其实就是Reservoir Sampling.

Wikipedia上的伪代码如下：

array R[k];    // result
integer i, j;

// fill the reservoir array
for each i in 1 to k do
    R[i] := S[i]
done;

// replace elements with gradually decreasing probability
for each i in k+1 to length(S) do
    j := random(1, i);   // important: inclusive range
    if j <= k then
        R[j] := S[i]
    fi
done

 

Java语言的实现如下：

public int[] samplingK(Scanner s, int k) {
	int[] res = new int[k];
	int i = 0;
	while (i < k) {
		res[i++] = s.nextInt();
	}
	Random r = new Random();
	while(s.hasNext()) {
		int num = s.nextInt();
		int rand = r.nextInt(i+1); // important: 0~i inclusive range 
		if(rand < k) {
			res[rand] = num;
		}
	}
	return res;
}

 

C语言的实现如下：

int i;
int b[k];

// All numbers are 100% sure to be chosen, if n=k
for (i = 0; i < k; i++)
    b[i] = getInput();

// Or if n > k, let's keep trying until no more input
while (stillHaveMoreInput() == true) {
    int t = getInput();
    i++;

    // The new number has k / i chance to be chosen
    if (rand(i) < k) {
        // OK, now we hit the k/i chance
        // Current number is chosen
        // But which old one should be replaced?
        // Each of the old one has equal chance 1/k
        b[rand(k)] = t;
    }    
}

以下是Google的一位工程师写的详细描述：

文章来自这里：http://gregable.com/2007/10/reservoir-sampling.html

Reservoir Sampling

Another, more complex option is reservoir sampling. First, you want to make a reservoir (array) of 1,000 elements and fill it with the first 1,000 elements in your stream. That way if you have exactly 1,000 elements, the algorithm works. This is the base case.

Next, you want to process the i'th element (starting with i = 1,001) such that at the end of processing that step, the 1,000 elements in your reservoir are randomly sampled amongst the i elements you've seen so far. How can you do this? Start with i = 1,001. With what probability after the 1001'th step should element 1,001 (or any element for that matter) be in the set of 1,000 elements? The answer is easy: 1,000/1,001. So, generate a random number between 0 and 1, and if it is less than 1,000/1,001 you should take element 1,001. In other words, choose to add element 1,001 to your reservoir with probability 1,000/1,001. If you choose to add it (which you likely will), then replace any element in the reservoir chosen randomly. I've shown that this produces a 1,000/1,001 chance of selecting the 1,001'th element, but what about the 2nd element in the list? The 2nd element is definitely in the reservoir at step 1,000 and the probability of it getting removed is the probability of element 1,001 getting selected multiplied by the probability of #2 getting randomly chosen as the replacement candidate. That probability is 1,000/1,001 * 1/1,000 = 1/1,001. So, the probability that #2 survives this round is 1 - that or 1,000/1,001.

This can be extended for the i'th round - keep the i'th element with probability 1,000/i and if you choose to keep it, replace a random element from the reservoir. It is pretty easy to prove that this works for all values of i using induction. It obviously works for the i'th element based on the way the algorithm selects the i'th element with the correct probability outright. The probability any element before this step being in the reservoir is1,000/(i-1). The probability that they are removed is 1,000/i * 1/1,000 = 1/i. The probability that each element sticks around given that they are already in the reservoir is (i-1)/i and thus the elements' overall probability of being in the reservoir after i rounds is 1,000/(i-1) * (i-1)/i = 1,000/i.

This ends up a little complex, but works just the same way as the random assigned numbers above.

 

 

 

Weighted Reservoir Sampling Variation
Now take the same problem above but add an extra challenge: How would you sample from a weighted distribution where each element has a given weight associated with it in the stream? This is sorta tricky. Pavlos S. Efraimidis figured out the solution in 2005 in a paper titled Weighted Random Sampling with a Reservoir. It works similarly to the assigning a random number solution above.

As you process the stream, assign each item a "key". For each item in the stream i, let 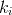 be the item's "key", let  be the weight of that item and let  be a random number between 0 and 1. The "key", 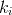, is a random number to the n'th root where n is weight of that item in the stream: . Now, simply keep the top n elements ordered by their keys, where n is the size of your sample. Easy.

To see how this works, lets start with non-weighted elements (ie: weight = 1).  is always 1, so the key is simply a random number and this algorithm degrades into the simple algorithm mentioned above.

Now, how does it work with weights? The probability of choosing i over j is the probability that 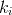 > 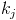.  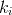can have any value from 0 - 1. However, it's more likely to be closer to 1 the higher w is. We can see what the distribution of this looks like when comparing to a weight 1 element by integrating k over all values of random numbers from 0 - 1. You get something like this:

k =

 

If w = 1, k = 1 / 2. If w = 9, k = 9 / 10. When replacing against a weight 1 element, an item of weight 5 would have a 50% chance and an element of weight 9 would have a 90% chance. Similar math works for two elements of non-zero weight.

Distributed Reservoir Sampling Variation
This is the problem that got me researching the weighted sample above. In both of the above algorithms, I can process the stream in O(N) time where N is length of the stream, in other words: in a single pass. If I want to break break up the problem on say 10 machines and solve it close to 10 times faster, how can I do that?

The answer is to have each of the 10 machines take roughly 1/10th of the input to process and generate their own reservoir sample from their subset of the data using the weighted variation above. Then, a final process must take the 10 output reservoirs and merge them.

The trick is that the final process must use the original "key" weights computed in the first pass. For example, If one of your 10 machines processed only 10 items in a size-10 sample, and the other 10 machines each processed 1 million items, you would expect that the one machine with 10 items would likely have smaller keys and hence be less likely to be selected in the final output. If you recompute keys in the final process, then all of the input items would be treated equally when they shouldn't.

 

如果想用Hadoop处理分布式处理的情况下，可以参考这里：

http://had00b.blogspot.com/2013/07/random-subset-in-mapreduce.html

MSDN里也有个很好的文章：

http://blogs.msdn.com/b/spt/archive/2008/02/05/reservoir-sampling.aspx

A simple random sampling strategy to produce a sample without replacement from a stream of data - that is, in one pass: O(N)

Want to sample s instances - uniformly at random without replacement - from a population size of n records, where n is not known.

Figuring out n would require 2 passes. Reservoir sampling achieves this in 1 pass. 
A reservoir R here is simply an array of size s. Let D be data stream of size n

Algorithm:

• Store first s elements into R.
• for each element in position k = s+1 to n ,
  • accept it with probability s/k
  • if accepted, choose a random element from R to replace.

Partial analysis:

Base case is trivial. For the k+1st case, the probability a given element i with position <= k is in R is s/k. The prob. i is replaced is the probability k+1st element is chosen multiplied by i being chosen to be replaced, which is: s/(k+1) * 1/s = 1/(k+1), and prob that i is not replaced is k/k+1.

So any given element's probability of lasting after k+1 rounds is: (chosen in k steps, and not removed in k steps)

= s/k * k/(k+1), which is s/(k+1).

So, when k+1 = n, any element is present with probability s/n.

Distributing Reservoir Sampling

It is very simple to distribute the reservoir sampling algorithm to n nodes.

Split the data stream into n partitions, one for each node. Apply reservoir sampling with reservoir size s, the final reservoir size, on each of the partitions. Finally, aggregate each reservoir into a final reservoir sample by carrying out reservoir sampling on them.

Lets say you split data of size n into 2 nodes, where each partition is of size n/2. Sub-reservoirs R1 and R2 are each of size s.

Probability that a record will be in sub-reservoir is: 
s / (n/2) = 2s/n

The Probability that a record will end up in the final reservoir given it is in a sub-reservoir is: s/(2s) = 1/2.

It follows that the probability any given record will end up in the final reservoir is: 
2s/n * 1/2 = s/n