(转)最长回文字串算法

来自（http://blog.163.com/zhaohai_1988/blog/static/2095100852012716105847112/）

 

最长回文子串 

 

 

 

    最长回文子串是最初我在网易笔试的时候遇见的，当时天真的把原字符串S倒转过来成为S‘，以为这样就将问题转化成为了求S和S’的最长公共子串的问题，而这个问题是典型的DP问题，我也在前面的文章中介绍了3中解决这个问题的方法。但是非常可惜，后来才知道这个算法是不完善的。那么到底为什么呢？听我慢慢道来。

S=“c a b a”  那么  S' = “a b a c”, 这样的情况下 S和 S‘的最长公共子串是aba。没有错误。

    但是当 S=“abacdfgdcaba”， 那么S’ = “abacdgfdcaba”。 这样S和S‘的最长公共子串是abacd。很明显abacd并不是S的最长回文子串，它甚至连回文都不是。

    现在是不是都明白为什么最长回文子串不能转化成为最长公共子串问题了。当原串S中含有一个非回文的串的反序串的时候，最长公共子串的解法就是不正确的。正如上一个例子中S既含有abacd，又含有abacd的反串cdaba，并且abacd又不是回文，所以转化成为最长公共子串的方法不能成功。除非每次我们求出一个最长公共子串的时候，我们检查一下这个子串是不是一个回文，如果是，那这个子串就是原串S的最长回文子串；如果不是，那么就去求下一个次长公共子串，以此类推。

 

最长回文子串有很多方法，分别是1暴力法，2 动态规划， 3 从中心扩展法，4 著名的manacher算法。下面我将分别介绍几种方法。

 

方法一 暴力法

遍历字符串S的每一个子串，去判断这个子串是不是回文，是回文的话看看长度是不是比最大的长度maxlength大。遍历每一个子串的方法要O（N2），判断每一个子串是不是回文的时间复杂度是O(N)，所以暴利方法的总时间复杂度是O（N3）。

 

方法二 动态规划 时间复杂度O(N2), 空间复杂度O(N2)

    动态规划就是暴力法的进化版本，我们没有必要对每一个子串都重新计算，看看它是不是回文。我们可以记录一些我们需要的东西，就可以在O（1）的时间判断出该子串是不是一个回文。这样就比暴力法节省了O（N）的时间复杂度哦，嘿嘿，其实优化很简单吧。

P（i，j）为1时代表字符串Si到Sj是一个回文，为0时代表字符串Si到Sj不是一个回文。

P（i，j）= P（i+1，j-1）（如果S[i] = S[j]）。这是动态规划的状态转移方程。

P（i，i）= 1，P（i，i+1）= if（S[i]= S[i+1]）

string longestPalindromeDP(string s){

  intn = s.length();

  intlongestBegin =0;

  intmaxLen =1;

  booltable[1000][1000]={false};

  for(inti =0; i < n; i++){

    table[i][i]=true;//前期的初始化

  }

  for(inti = 0; i < n-1; i++) {

    if(s[i] == s[i+1]) {

      table[i][i+1] = true; //前期的初始化

      longestBegin = i;

      maxLen = 2;

    }

  }

  for(intlen = 3; len <= n; len++) {

    for(inti = 0; i < n-len+1; i++) {

      intj = i+len-1;

      if(s[i] == s[j] && table[i+1][j-1]) {

        table[i][j] = true;

        longestBegin = i;

        maxLen = len;

      }

    }

  }

  returns.substr(longestBegin, maxLen);

}

 

方法三 中心扩展法

    这个算法思想其实很简单啊，时间复杂度为O（N2），空间复杂度仅为O（1）。就是对给定的字符串S，分别以该字符串S中的每一个字符C为中心，向两边扩展，记录下以字符C为中心的回文子串的长度。但是有一点需要注意的是，回文的情况可能是 a b a，也可能是 a b b a。

string expandAroundCenter(string s,intc1,intc2){

  intl = c1, r = c2;

  intn = s.length();

  while(l >=0&& r <= n-1&& s[l]== s[r]){

    l--;

    r++;

  }

  returns.substr(l+1, r-l-1);

}

string longestPalindromeSimple(string s){

  intn = s.length();

  if(n ==0)return"";

  string longest = s.substr(0,1);  // a single char itself is a palindrome

  for(inti = 0; i < n-1; i++) {

    string p1 = expandAroundCenter(s, i, i);

    if(p1.length() > longest.length())

      longest = p1;

    string p2 = expandAroundCenter(s, i, i+1);

    if(p2.length() > longest.length())

      longest = p2;

  }

  returnlongest;

}

  方法四 传说中的Manacher算法。时间复杂度O(N)

    这个算法有一个很巧妙的地方，它把奇数的回文串和偶数的回文串统一起来考虑了。这一点一直是在做回文串问题中时比较烦的地方。这个算法还有一个很好的地方就是充分利用了字符匹配的特殊性，避免了大量不必要的重复匹配。

    算法大致过程是这样。先在每两个相邻字符中间插入一个分隔符，当然这个分隔符要在原串中没有出现过。一般可以用‘#’分隔。这样就非常巧妙的将奇数长度回文串与偶数长度回文串统一起来考虑了（见下面的一个例子，回文串长度全为奇数了），然后用一个辅助数组P记录以每个字符为中心的最长回文串的信息。P［id］记录的是以字符str［id］为中心的最长回文串，当以str［id］为第一个字符，这个最长回文串向右延伸了P［id］个字符。
    原串：    w aa bwsw f d
    新串:           #  w  # a # a #  b  # w # s # w #  f  # d #
辅助数组P：1  2  1 2 3 2 1  2  1  2 1 4 1 2 1  2 1 2 1

这里有一个很好的性质，P［id］-1就是该回文子串在原串中的长度（包括‘#’）。如果这里不是特别清楚，可以自己拿出纸来画一画，自己体会体会。当然这里可能每个人写法不尽相同，不过我想大致思路应该是一样的吧。

现在的关键问题就在于怎么在O（n）时间复杂度内求出P数组了。只要把这个P数组求出来，最长回文子串就可以直接扫一遍得出来了。

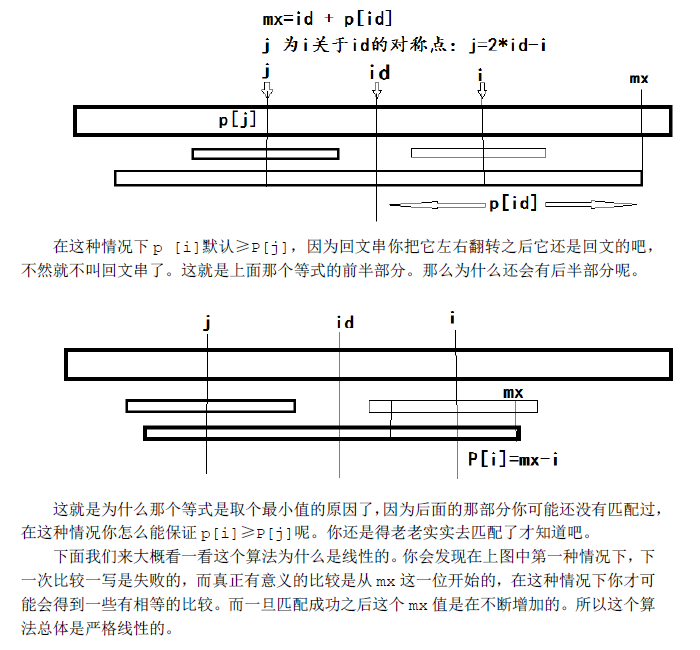
    那么怎么计算P[i]呢？该算法增加两个辅助变量（其实一个就够了，两个更清晰）id和mx，其中id表示最大回文子串中心的位置，mx则为id+P[id]，也就是最大回文子串的边界。

    然后可以得到一个非常神奇的结论，这个算法的关键点就在这里了：如果mx > i，那么

P[i] >= MIN(P[2 * id - i], mx - i)。就是这个串卡了我非常久。实际上如果把它写得复杂一点，理解起来会简单很多：

 

//记j = 2 * id - i，也就是说 j 是 i 关于 id 的对称点。
if (mx - i > P[j]) 
    P[i] = P[j];
else /* P[j] >= mx - i */
    P[i] = mx - i; // P[i] >= mx - i，取最小值，之后再匹配更新。

当 mx - i > P[j] 的时候，以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中，由于 i 和 j 对称，以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中，所以必有 P[i] = P[j]。

当 P[j] > mx - i 的时候，以S[j]为中心的回文子串不完全包含于以S[id]为中心的回文子串中，但是基于对称性可知，也就是说以S[i]为中心的回文子串，其向右至少会扩张到mx的位置，也就是说 P[i] >= mx - i。至于mx之后的部分是否对称，就只能老老实实去匹配了。

由于这个算法是线性从前往后扫的。那么当我们准备求P［i］的时候，i以前的P［j］我们是已经得到了的。我们用mx记在i之前的回文串中，延伸至最右端的位置。同时用id这个变量记下取得这个最优mx时的id值。（注：为了防止字符比较的时候越界，我在这个加了‘#’的字符串之前还加了另一个特殊字符‘$’，故我的新串下标是从1开始的）

#include<vector>
#include<iostream>
usingnamespace std;

constint N=300010;
int n, p[N];
char s[N], str[N];

#define _min(x, y)((x)<(y)?(x):(y))

void kp()
{
int i;
int mx =0;
int id;
for(i=n; str[i]!=0; i++)
str[i]=0;//没有这一句有问题。。就过不了ural1297，比如数据：ababa aba
for(i=1; i<n; i++)
{
if( mx > i )
p[i]= _min( p[2*id-i], p[id]+id-i );
else
p[i]=1;
for(; str[i+p[i]]== str[i-p[i]]; p[i]++)
;
if( p[i]+ i > mx )
{
mx = p[i]+ i;
id = i;
}
}
}

void init()
{
int i, j, k;
str[0]='$';
str[1]='#';
for(i=0; i<n; i++)
{
str[i*2+2]= s[i];
str[i*2+3]='#';
}
n = n*2+2;
s[n]=0;
}

int main()
{
int i, ans;
while(scanf("%s", s)!=EOF)
{
n = strlen(s);
init();
kp();
ans =0;
for(i=0; i<n; i++)
if(p[i]>ans)
ans = p[i];
printf("%d\n", ans-1);
}
return0;
}

 

if( mx > i)

p[i]=MIN( p[2*id-i], mx-i);

 

就是当前面比较的最远长度mx>i的时候，P［i］有一个最小值。这个算法的核心思想就在这里，为什么P数组满足这样一个性质呢?

（下面的部分为图片形式）