Reference: https://web.cs.ship.edu/~tbriggs/dynamic/
The Integer Knapsack problem is a famous rubrick in Computer Science. The problem has a simple brute-force solution. However, solving large instances of this problem requires considerable work (run-time).
The problem is often given as a story:
| Item | Size | Value |
| 1 - ring | 1 | 15 |
| 2 - candelabra | 5 | 10 |
| 3 - radio | 3 | 9 |
| 4 - elvis | 4 | 5 |
The problem is, which items should the thief take? If the knapsack were large enough, the thief could take all of the items and run. But, that is not the case (the problem states that the knapsack cannot hold all of the items). There are three types of "thieves" that we shall consider: a greedy thief, a foolish and slow thief, and a wise thief. Each of these thieves have a knapsack that can old a total size of 8.
The greedy thief breaks into the window, and sees the items. He makes a mental list of the items available, and grabs the most expensive item first. The ring goes in first, leaving a capacity of 7, and a value of 15. Next, he grabs the candelabra, leaving a knapsack of size 2 and a value of 25. No other items will fit in his knapsack, so he leaves.
The foolish and slow thief climbs in the window, and sees the items. This thief was a programmer, downsized as part of the "dot-bomb" blowout. Possessing a solid background in boolean logic, he figures that he can simply compute all combinations of the objects and choose the best. So, he starts going through the binary combinations of objects - all 2^5 of them. While he is still drawing the truth table, the police show up, and arrest him. Although his solution would certainly have given him the best answer, it just took long to compute.
The wise thief appears, and observes the items. He notes that an empty knapsack has a value of 0. Further, he notes that a knapsack can either contain each item, or not. Further, his decision to include an item will be based on a quick calculation - either the knapsack with some combination of the previous items will be worth more, or else the knapsack of a size that will fit the current item was worth more. So, he does this quick computation, and figures out that the best knapsack he can take is made up of items 1,3, and 4, for a total value of 29.
Greedy Algorithms
The mistake the first thief made was that he was too greedy. He took the items in non-decreasing order by their value. He ended up with a knapsack that was not completely filled. Not having a knapsack filled completely does not necessarily imply that the solution will be bad, but it is often the case.
One advantage to this technique is that it can be done very quickly. The amount of work for this solution is relative to how many objects the thief has to look at. In the worst case, how many items would this be? How much work is involved?
The greedy algorithm does not work for this version of the problem; but there is another closely related version. Suppose that instead of objects, there were piles of dust. The first pile was platinum dust, the second pile was gold, and the third pile were silver dust. In this version of the problem, the thief will fill his sack with as much as the sack will hold. If there were still capacity, the thief will next fill the sack with gold, and finally, silver. This version of the problem is often called the "Continuous Knapsack" problem.
Q: What key difference is there in the continuous problem that makes a greedy solution work?
Brute Force
The mistake the second thief in our rubric made was to try to enumerate all of the possible choices. There are 25 combinations in this example. Expressed more generally, there are 2n combinations of items that the thief can choose. This can be expressed as the power set of the items. Algorithms that require enumeration of this set will require exponential work: O(2n). Clearly, as the size of the set increases, the amount of work will increase exponentially.
Dynamic Programming
The wise thief used a technique that is known as "dynamic programming." In this case, a table was made to track "the best knapsack so far." The complete table that is show in subsequent examples is for demonstration purposes. In the following example, there is a column that indicates a range of values from 0 to the 9. This corresponds to the "target weight" of the knapsack. The table stops at the maximum capacity of the knapsack. There are then n+1 columns, one each for the items that can be selected.
The first column is initialized to zero. Logically, this corresponds to a knapsack with zero items having zero worth. The first row is also initialized to zero, corresponding to a knapsack of zero capacity.
Finally, the values of the table are filled in, from left to right, and from top to bottom. For each cell item, the total worth of a knapsack is determined as either the worth of a knapsack without the current item (expressed as the value directly to the left of the current value), or it is the value of the knapsack with the current item added into it.
| Items> Capacity |
i:1 15/1 |
i:2 10/5 |
i:3 9/3 |
i:4 5/4 |
|
| 0 | 0^ | 0^ | 0^ | 0^ | 0^ |
| 1 | 0^ | 15^ | 15^ | 15^ | 15^ |
| 2 | 0^ | 15^ | 15^ | 15^ | 15^ |
| 3 | 0^ | 15^ | 15^ | 15< | 15^ |
| 4 | 0^ | 15^ | 15^ | 24^ | 24< |
| 5 | 0^ | 15^ | 15< | 24^ | 24< |
| 6 | 0^ | 15^ | 25^ | 25< | 25< |
| 7 | 0^ | 15^ | 25^ | 25< | 25< |
| 8 | 0^ | 15^ | 25^ | 25< | 29^ |
Observe in the previous example, the knapsack starts at zero, and the computation continues down the first column. Since the first item has a size of one, a knapsack of value 15 can be made for all of the columns. The next column shows that knapsacks less than size 5 can only be made using an empty knapsack or else using only the first item. For knapsacks over size six, then a decision must be made: is it better to build a knapsack with both items, or only with one of them.
What makes this different than the greedy algorithm happens when processing the third item. First, notice that the best knapsack that can be made, up until size four, does not include the third item. Then, when the capacity of the knapsack increases enough to hold the third item, the value changes - the value of the knapsack now includes the second and third items, for a total value of 25. Finally, when the capacity is large enough to hold all three items, then the capacity is grown to hold all three items. However, following the same pattern for the fourth item, it is apparent that algorithm works by showing that including the fourth item in place of any other item is not required.
A More Concise Definition
Let S={s1,s2,..sn} be a set of weights, and V={v1,v2,..vn}. Let t be a target capacity, representing the largest total weight the knapsack can hold. A solution to the knapsack problem is:
![]() and
and ![]()
The solution will be the one with the maximum value, ,and the minimum weight. The group {0,1} serves to indicate that the item is either in the knapsack, or it is not.
Recurrence Relation
One approach to solving this problem is to break the problem down in terms of its sub-problems. Consider trying to build a knapsack of size W. The question to answer is, should item i be included in the knapsack or not. Including item i should make a knapsack of higher value than all previous knapsacks of size W. But, if the knapsack is already at size W, including item i will make the knapsack too large. So, the solution has to examine a knapsack of size W-wi. Specifically, consider a knapsack of size W-wi that does not include item i. To decide if the item should be included in the knapsack, compare the values of the knapsack of size W that does not include the current item; and the value of a knapsack of size W-wi + the value of item i. If the worth of the knapsack is increased by taking including the item, that item i will be included in the knapsack, and its overall value will be increased. So, a recurrence relation can be developed:

Solving this recursive version of the knapsack problem will return the correct answer, but will be very inefficient. Note that it will repeatedly solve the same set of sub-problems, generating a series of recursive calls that will grow as the recursive Fibonacci sequence did.
Memoization
The dynamic programming version of this problem is essentially a memoization approach to solving this problem. Instead of repeatedly solving the same sub-problems, create a table that contains the results of previous evaluations of the sub-problems, and using that to increase the speed of the solution. The table must contain k rows (the target capacity), and i columns (the number of items). Ignoring boundary conditions, each cell of the table can be computed using the following function:
max( T[i-1,j], vi + T[i-1, j-wi] )
It is this memoization approach that leads to the final pseudo-code solution to the problem:
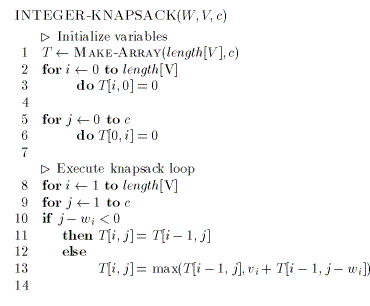
This pseudo-code is extremely similar to the previous recurrence relation. The major difference is that this algorithm starts at the smallest knapsack and grows to fill the final table. The recurrence relation starts at the largest solution and solves to the smallest.
Run-Time Analysis
The run-time of this knapsack will depend on the size of the table. Its two factors were k rows (determined by the target capacity), and the n columns (the number of items in the set. So, the run-time of this version will be θ(k*n). Caution should be observed here: k is not a constant, and its size may be considerably larger than the number of items in the set. This is a type of algorithm that exhibits pseudo-polynomial time.
pseudo-polynomial time
def. An algorithm whose runtime is bound not only on the size of the input (e.g. n items), but also on the magnitude of the inputs of the problem.
One approach to "fixing" this problem is the Approximate Knapsack Problem.
Why Study the Knapsack Problem?
Since most people are not thieves, the knapsack problem may not seem to of much practical import. The knapsack-problem was used as the basis for acryptographic system (that has since been broken). However, the problem arises in several constraint satisfacation problems (CSP). Consider any problem where the solution depends on selecting some number of items whose values are maximized (or minimized), and whoose weight is equal to a target value.
Java Source Code
public int integerKnapsack(int[] weights, int[] values, int capacity) {
int[][] d = new int[weights.length+1][capacity+1];
for(int i=1; i<=weights.length; i++) {
for(int j=1; j<=capacity; j++) {
if(weights[i-1] > j) {
d[i][j] = d[i-1][j];
} else {
d[i][j] = Math.max(d[i-1][j], d[i-1][j-weights[i-1]]+values[i-1]);
}
}
}
return d[weights.length][capacity];
}
public void testIntegerKnapsack() {
int[] weights = {1,5,3,4};
int[] values = {15,10,9,5};
int capacity = 8;
int maxValue = integerKnapsack(weights, values, capacity);
System.out.println(maxValue);
}
Reference:







相关推荐
5. 整数背包问题(Integer Knapsack) 整数背包问题是背包问题的一种,要求在不超过背包容量的前提下,选择若干物品使得总价值最大。这个问题可以通过动态规划方法,在多项式时间内解决。 6. 编辑距离(Edit Distance...
2)Dynamic Programming is an algorithm design method that can be used when the solution to a problem may be viewed as the result of a sequence of decisions and this algorithm is a very useful technique...
在MATLAB中实现这些功能时,通常会用到动态规划(Dynamic Programming)方法,因为这种方法能够有效地找到最优解,并且时间复杂度相对较低。具体来说,我们可以创建一个二维数组,其中每一行代表一个物品,每一列...
Qt 采用http通信json解析读取天气
岗位晋升360度调查表.doc
合法辞退员工的N种方式.pptx
大模型、Agent、具身智能及人形机器人学习全路径规划.pdf
华润万家员工手册.doc
招聘需求分析.xls
内容概要:本文详细介绍了基于‘光伏(PV)+蓄电池+负载’架构的双有源桥DC-DC变换器仿真方法及其在Matlab 2021b中的具体实现。首先解析了光伏系统的MPPT控制,通过扰动观察法使光伏板始终处于最大功率点。接着讨论了蓄电池的恒流充放电控制,利用PI控制器确保电池的安全和高效运作。然后阐述了双有源桥DC-DC变换器的闭环控制机制,借助PID控制器维持系统输出电压的稳定性。最后,文章展示了如何在Matlab Simulink环境下构建完整的仿真模型,涵盖各模块间的电气连接与信号交互,为新能源系统的优化提供了理论和技术支持。 适合人群:从事电力电子、新能源系统设计的研究人员和工程师,尤其是那些需要深入了解光伏储能系统工作原理的人群。 使用场景及目标:适用于希望掌握光伏储能系统中关键组件如MPPT、恒流充放电控制及双有源桥DC-DC变换器的设计与仿真的技术人员。目标是在实际工程项目中提高系统的效率和可靠性。 其他说明:文中提供的代码片段和建模思路有助于读者更好地理解和实践相关技术,同时也强调了一些常见的陷阱和调试技巧,帮助避免潜在的问题。
线性代数
内容概要:本文详细介绍了不同类型电机的调速方法,重点探讨了直流电机双闭环调速、永磁同步电机电流滞环闭环调速以及异步电机滞环电流调速。文中不仅提供了每种调速方法的基本原理和技术特点,还附带了相应的代码示例进行辅助解释。此外,文章对永磁同步电机的电流滞环调速与SVPWM调速进行了对比,指出了各自的优劣之处。最后,强调了在实际应用中选择合适调速方案的重要性。 适合人群:从事电机控制系统设计与开发的技术人员,尤其是有一定电机控制基础的研发人员。 使用场景及目标:适用于需要深入了解电机调速机制及其应用场景的专业人士。目标是帮助读者掌握不同电机调速方法的特点,以便在实际工程中做出最优选择。 其他说明:文章通过具体的代码实例展示了调速方法的实际应用,使读者能够更好地理解和实践相关技术。同时提醒读者在实际调试过程中要注意参数设置和硬件条件的影响。
人员晋升推荐表.xls
员工生日关怀方案
内容概要:本文详细介绍了对国际知名大厂的三个逆向ADC电路(SAR ADC、Sigma-Delta ADC和Pipeline ADC)进行深入剖析。作者通过Cadence Virtuoso平台研究了这些电路的标准单元库设计,探讨了各个电路的关键技术和实现细节。对于24bit Sigma-Delta ADC,重点讨论了其调制器部分的时钟相位分配和噪声整形技术;对于16bit SAR ADC,则关注其比较器阵列的独特设计以及动态锁存比较器的应用;而对于14bit Pipeline ADC,着重分析了其级间放大器设计和电荷共享技术。此外,文中还提到了在将这些设计适配到自家工艺过程中遇到的问题及其解决方案,如电容寄生效应、时序约束调整、运放结构优化等。 适合人群:从事模拟集成电路设计的专业人士,尤其是对ADC设计感兴趣的工程师和技术研究人员。 使用场景及目标:帮助读者深入了解高精度ADC的工作原理和设计技巧,掌握逆向工程技术在实际项目中的应用,提高对不同工艺节点下ADC设计的理解和适应能力。 其他说明:文中提供了大量具体的代码片段和仿真命令,便于读者理解和实践。同时,作者分享了许多宝贵的经验教训,强调了在逆向工程中需要注意的技术细节和潜在风险。
内容概要:本文详细介绍了大型立体仓库智能物流系统的构建与优化。该项目涉及一万多个库位、一百多台输送机和八台堆垛机,采用了西门子PLC作为控制核心,通过无线网桥与WCS和WMS系统对接。文章重点讲解了梯形图编程和功能块的应用,如输送机启停控制、堆垛机移动控制、路径规划、无线通讯处理以及异常处理机制。此外,还探讨了设备协同、逻辑优化、任务分配算法和速度曲线规划等方面的技术细节。 适合人群:从事工业自动化、智能仓储系统设计与开发的工程师和技术爱好者。 使用场景及目标:适用于智能仓储系统的设计、实施和维护,旨在提高系统的稳定性、效率和可维护性。 其他说明:文中提供了大量实际项目中的代码示例和调试经验,有助于读者理解和应用相关技术。
新员工月工作总结表.xlsx
内容概要:本文详细介绍了基于西门子S7-1500 PLC的汽车电子零件装配线集成解决方案。主要内容涵盖伺服轴控制、阿特拉斯拧紧枪控制、康耐视视觉检测系统以及HMI界面的设计与实现。文中展示了如何利用SCL语言将多种工业设备(如HMI、伺服电机、六轴机器人等)的功能封装为标准化功能块,从而提高系统的模块化程度和可复用性。同时,还分享了一些实际项目中的调试经验和优化技巧,如通过调整加减速曲线避免机械振动、设置扭矩保持时间和视觉检测的防抖定时器等。 适合人群:从事自动化控制领域的工程师和技术人员,尤其是熟悉PLC编程和工业自动化设备集成的专业人士。 使用场景及目标:适用于汽车制造行业的生产线控制系统设计与实施。主要目标是帮助工程师快速掌握如何使用SCL语言构建高效稳定的PLC控制系统,提升生产效率和产品质量。 其他说明:文中不仅提供了详细的代码示例,还结合具体的应用场景进行了深入剖析,有助于读者更好地理解和应用相关技术。此外,强调了模块化编程的优势,如减少重复劳动、便于维护升级等。
内容概要:本文详细介绍了如何在STM32、AT32和GD32等Cortex-M系列MCU上实现串口IAP(In Application Programming)Bootloader,支持远程升级及RS485升级。主要内容涵盖Bootloader的工作原理、内存分配、通信协议设计、Flash写入操作以及跳转应用程序的关键步骤。文中提供了具体的代码示例,如Bootloader主循环、RS485收发控制、Flash写入、CRC校验等,并分享了多个实战经验和注意事项,确保数据传输的可靠性。 适合人群:从事嵌入式系统开发的技术人员,尤其是对STM32、AT32、GD32等国产MCU有一定了解并希望掌握串口IAP技术的研发人员。 使用场景及目标:适用于需要远程升级固件的嵌入式项目,帮助开发者避免现场升级带来的不便,提高设备维护效率。目标是让读者能够独立实现一个可靠的串口IAP Bootloader,掌握RS485通信和Flash编程的关键技术。 其他说明:文中提到的代码和配置已在GitHub上提供,方便读者下载和实践。同时,作者分享了许多实战经验和常见问题解决方案,有助于减少开发过程中可能出现的问题。
线性代数