3.1、摘要
在前面两篇文章中,分别介绍和讨论了朴素贝叶斯分类与贝叶斯网络两种分类算法。这两种算法都以贝叶斯定理为基础,可以对分类及决策问题进行概率推断。在这一篇文章中,将讨论另一种被广泛使用的分类算法——决策树(decision tree)。相比贝叶斯算法,决策树的优势在于构造过程不需要任何领域知识或参数设置,因此在实际应用中,对于探测式的知识发现,决策树更加适用。
3.2、决策树引导
通俗来说,决策树分类的思想类似于找对象。现想象一个女孩的母亲要给这个女孩介绍男朋友,于是有了下面的对话:
女儿:多大年纪了?
母亲:26。
女儿:长的帅不帅?
母亲:挺帅的。
女儿:收入高不?
母亲:不算很高,中等情况。
女儿:是公务员不?
母亲:是,在税务局上班呢。
女儿:那好,我去见见。
这个女孩的决策过程就是典型的分类树决策。相当于通过年龄、长相、收入和是否公务员对将男人分为两个类别:见和不见。假设这个女孩对男人的要求是:30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员,那么这个可以用下图表示女孩的决策逻辑(声明:此决策树纯属为了写文章而YY的产物,没有任何根据,也不代表任何女孩的择偶倾向,请各位女同胞莫质问我^_^):
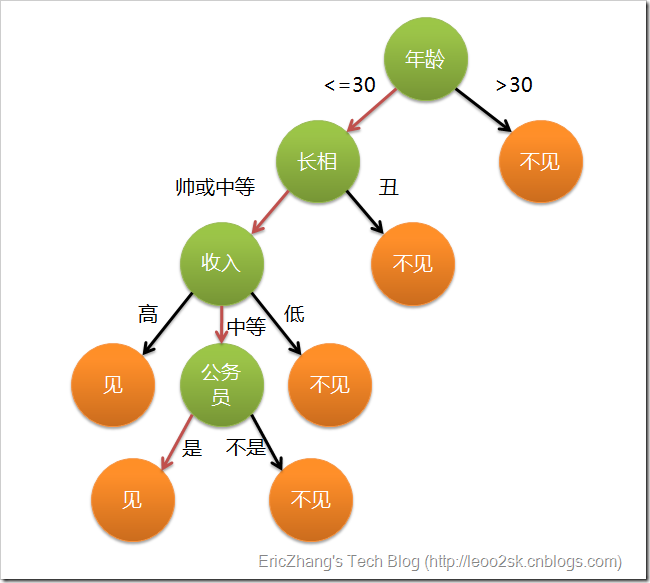
上图完整表达了这个女孩决定是否见一个约会对象的策略,其中绿色节点表示判断条件,橙色节点表示决策结果,箭头表示在一个判断条件在不同情况下的决策路径,图中红色箭头表示了上面例子中女孩的决策过程。
这幅图基本可以算是一颗决策树,说它“基本可以算”是因为图中的判定条件没有量化,如收入高中低等等,还不能算是严格意义上的决策树,如果将所有条件量化,则就变成真正的决策树了。
有了上面直观的认识,我们可以正式定义决策树了:
决策树(decision tree)是一个树结构(可以是二叉树或非二叉树)。其每个非叶节点表示一个特征属性上的测试,每个分支代表这个特征属性在某个值域上的输出,而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始,测试待分类项中相应的特征属性,并按照其值选择输出分支,直到到达叶子节点,将叶子节点存放的类别作为决策结果。
可以看到,决策树的决策过程非常直观,容易被人理解。目前决策树已经成功运用于医学、制造产业、天文学、分支生物学以及商业等诸多领域。知道了决策树的定义以及其应用方法,下面介绍决策树的构造算法。
3.3、决策树的构造
不同于贝叶斯算法,决策树的构造过程不依赖领域知识,它使用属性选择度量来选择将元组最好地划分成不同的类的属性。所谓决策树的构造就是进行属性选择度量确定各个特征属性之间的拓扑结构。
构造决策树的关键步骤是分裂属性。所谓分裂属性就是在某个节点处按照某一特征属性的不同划分构造不同的分支,其目标是让各个分裂子集尽可能地“纯”。尽可能“纯”就是尽量让一个分裂子集中待分类项属于同一类别。分裂属性分为三种不同的情况:
1、属性是离散值且不要求生成二叉决策树。此时用属性的每一个划分作为一个分支。
2、属性是离散值且要求生成二叉决策树。此时使用属性划分的一个子集进行测试,按照“属于此子集”和“不属于此子集”分成两个分支。
3、属性是连续值。此时确定一个值作为分裂点split_point,按照>split_point和<=split_point生成两个分支。
构造决策树的关键性内容是进行属性选择度量,属性选择度量是一种选择分裂准则,是将给定的类标记的训练集合的数据划分D“最好”地分成个体类的启发式方法,它决定了拓扑结构及分裂点split_point的选择。
属性选择度量算法有很多,一般使用自顶向下递归分治法,并采用不回溯的贪心策略。这里介绍ID3和C4.5两种常用算法。
3.3.1、ID3算法
从信息论知识中我们直到,期望信息越小,信息增益越大,从而纯度越高。所以ID3算法的核心思想就是以信息增益度量属性选择,选择分裂后信息增益最大的属性进行分裂。下面先定义几个要用到的概念。
设D为用类别对训练元组进行的划分,则D的熵(entropy)表示为:
其中pi表示第i个类别在整个训练元组中出现的概率,可以用属于此类别元素的数量除以训练元组元素总数量作为估计。熵的实际意义表示是D中元组的类标号所需要的平均信息量。
现在我们假设将训练元组D按属性A进行划分,则A对D划分的期望信息为:
而信息增益即为两者的差值:
ID3算法就是在每次需要分裂时,计算每个属性的增益率,然后选择增益率最大的属性进行分裂。下面我们继续用SNS社区中不真实账号检测的例子说明如何使用ID3算法构造决策树。为了简单起见,我们假设训练集合包含10个元素:
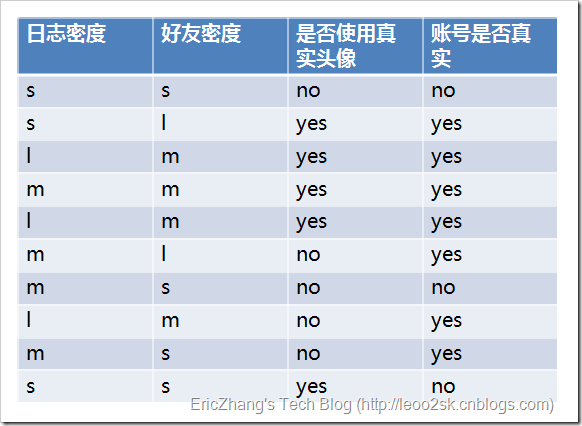
其中s、m和l分别表示小、中和大。
设L、F、H和R表示日志密度、好友密度、是否使用真实头像和账号是否真实,下面计算各属性的信息增益。
因此日志密度的信息增益是0.276。
用同样方法得到H和F的信息增益分别为0.033和0.553。
因为F具有最大的信息增益,所以第一次分裂选择F为分裂属性,分裂后的结果如下图表示:
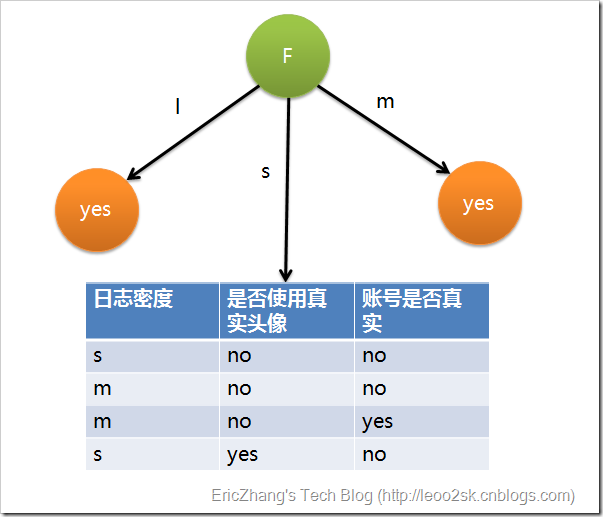
在上图的基础上,再递归使用这个方法计算子节点的分裂属性,最终就可以得到整个决策树。
上面为了简便,将特征属性离散化了,其实日志密度和好友密度都是连续的属性。对于特征属性为连续值,可以如此使用ID3算法:
先将D中元素按照特征属性排序,则每两个相邻元素的中间点可以看做潜在分裂点,从第一个潜在分裂点开始,分裂D并计算两个集合的期望信息,具有最小期望信息的点称为这个属性的最佳分裂点,其信息期望作为此属性的信息期望。
3.3.2、C4.5算法
ID3算法存在一个问题,就是偏向于多值属性,例如,如果存在唯一标识属性ID,则ID3会选择它作为分裂属性,这样虽然使得划分充分纯净,但这种划分对分类几乎毫无用处。ID3的后继算法C4.5使用增益率(gain ratio)的信息增益扩充,试图克服这个偏倚。
C4.5算法首先定义了“分裂信息”,其定义可以表示成:
其中各符号意义与ID3算法相同,然后,增益率被定义为:
C4.5选择具有最大增益率的属性作为分裂属性,其具体应用与ID3类似,不再赘述。
3.4、关于决策树的几点补充说明
3.4.1、如果属性用完了怎么办
在决策树构造过程中可能会出现这种情况:所有属性都作为分裂属性用光了,但有的子集还不是纯净集,即集合内的元素不属于同一类别。在这种情况下,由于没有更多信息可以使用了,一般对这些子集进行“多数表决”,即使用此子集中出现次数最多的类别作为此节点类别,然后将此节点作为叶子节点。
3.4.2、关于剪枝
在实际构造决策树时,通常要进行剪枝,这时为了处理由于数据中的噪声和离群点导致的过分拟合问题。剪枝有两种:
先剪枝——在构造过程中,当某个节点满足剪枝条件,则直接停止此分支的构造。
后剪枝——先构造完成完整的决策树,再通过某些条件遍历树进行剪枝。
关于剪枝的具体算法这里不再详述,有兴趣的可以参考相关文献。
张洋 http://www.cnblogs.com/leoo2sk/archive/2010/09/19/decision-tree.html








相关推荐
朴素贝叶斯分类是一种基于概率理论的分类算法,它的核心思想源自贝叶斯定理。贝叶斯定理允许我们在已知某一条件下另一个事件发生的概率时,反向计算出在该事件发生条件下另一条件的概率。在分类问题中,这被用来预测...
在"DecisionTree"压缩包中,可能包含了实现决策树的Java源代码,包括数据结构定义、决策树构建函数、特征选择算法、训练和预测接口等。通过阅读和理解这些代码,可以进一步掌握决策树的实现细节。 总之,决策树是一...
标题"Decision Tree Excel 插件,决策树"所涉及的知识点主要包括: 1. **决策树概念**:决策树是一种图形表示方法,由节点和边组成,其中每个内部节点代表一个特征或属性测试,每个分支代表测试的一种结果,而叶...
在Python中实现决策树算法,首先需要导入相关的库,如`sklearn.tree`和`sklearn.datasets`。`sklearn.tree`包含了决策树模型的构建和评估工具,而`sklearn.datasets`可以用来加载数据集,如鸢尾花(Iris)数据集,这...
接着,实现决策树的核心类`DecisionTree`,这个类应包含以下关键功能: 1. **初始化**:设置决策树的参数,如最大深度、最小样本数等。 2. **训练**:根据输入的训练集,使用选定的分裂策略(如ID3、C4.5或CART)...
资源中包括决策树分类算法、朴素贝叶斯分类算法、人工神经网络分类算法的代码(.ipynb,.py)和案例股票价格波动分析的数据(.csv),建议使用jupyter notebook打开.ipynb文件,体验更佳 1、资源配合博文《【python...
decision-tree-js, ID3决策树的小型JavaScript实现 decision-tree-js决策树与随机森林分类器算法的小型JavaScript实现算法。随机森林演示在线演示:http://fiddle.jshell.net/7WsMf/show/light/ 决策树演示在线演示...
决策树算法基于一系列规则对数据进行分割,通过构建树状结构来做出预测或决策。在遥感领域,决策树可以用来解析影像数据,如识别地物类型、估计植被覆盖度、检测变化等。"batch"一词指的是这种算法的批量处理能力,...
决策树算法是一种既可用于分类也有用于回归的监督机器学习算法,优点是易于理解和实现,并且能够在较短时间内对大数据进行较为准确的分析和预测。决策树算法的原理是基于训练数据集构建一个树状决策树模型,即一个 ...
《神经网络算法与实现——基于Java语言 代码实例》是一本深入探讨神经网络编程的书籍,专注于使用Java语言实现各种神经网络模型。本书通过实际的代码示例,为读者提供了理解神经网络工作原理以及如何在Java环境下...
二叉决策树是一种广泛应用的机器学习算法,尤其在分类问题中表现出色。它通过一系列基于特征的简单规则来做出决定...通过深入研究`decisionTree.m`,可以更好地理解和应用决策树算法,同时为其他机器学习任务提供基础。
3.1 决策树(decision tree)算法
本实验报告主要关注的是决策树算法的实践应用,旨在帮助学生理解其分类原理和实现过程。 实验原理基于决策树学习和分类,决策树通过不断选择最优属性进行划分,以最大化信息增益或基尼指数,直到所有样本属于同一...
这个算法由Ross Quinlan在1986年提出,是构建决策树的基础方法之一,为后来的C4.5和CART等决策树算法奠定了基础。ID3的主要思想是通过信息熵和信息增益来选择最优属性进行划分,逐步构建决策树。 1. **决策树的基本...
决策树(Decision Tree)是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。由于这种决策分支画...
基于MapReduce实现决策树算法的知识点 基于MapReduce实现决策树算法是一种使用MapReduce框架来实现决策树算法的方法。在这个方法中,主要使用Mapper和Reducer来实现决策树算法的计算。下面是基于MapReduce实现决策...
决策树是一种广泛应用于数据挖掘和机器学习的算法,它的核心思想是通过一系列的规则划分,将数据集分割成不同的类别。在这个案例中,我们将详细探讨如何利用Python来实现决策树对鸢尾花数据集的分类,并对其进行可视...
在这个"决策树(DecisionTree)项目"中,我们将深入探讨如何使用Python实现决策树算法。 首先,Python中的`sklearn`库提供了方便的接口来实现决策树模型。`sklearn.tree`模块包含了`DecisionTreeClassifier`和`...
`rpart`库是基于R的`rpart`包的一个Python接口,而`sklearn`库的`tree`模块虽然没有直接实现C5.0,但可以使用其决策树算法作为近似替代。 3. **模型构建**:使用C5.0函数训练决策树模型。在`rpart`中,调用`rpart()...
决策树算法是数据挖掘和机器学习领域中一个非常重要的分类方法,它通过一系列规则对数据集进行分治,直到每个分支都对应一个单一的类别为止。决策树是基于监督学习方法实现的,这意味着它需要一个事先已标记的数据集...