K Best（二分搜索）

K Best

Time Limit: 8000MS		Memory Limit: 65536K
Total Submissions: 5288		Accepted: 1431
Case Time Limit: 2000MS		Special Judge

Description

Demy has n jewels. Each of her jewels has some value v_i and weight w_i.

Since her husband John got broke after recent financial crises, Demy has decided to sell some jewels. She has decided that she would keep k best jewels for herself. She decided to keep such jewels that their specific value is as large as possible. That is, denote the specific value of some set of jewels S = {i₁, i₂, …, i_k} as

.

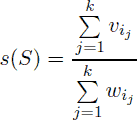Demy would like to select such k jewels that their specific value is maximal possible. Help her to do so.

Input

The first line of the input file contains n — the number of jewels Demy got, and k — the number of jewels she would like to keep (1 ≤ k ≤ n ≤ 100 000).

The following n lines contain two integer numbers each — v_i and w_i (0 ≤ v_i ≤ 10⁶, 1 ≤ w_i ≤ 10⁶, both the sum of all v_i and the sum of all w_i do not exceed 10⁷).

Output

Output k numbers — the numbers of jewels Demy must keep. If there are several solutions, output any one.

Sample Input

3 2
1 1
1 2
1 3

Sample Output

1 2

 

       题意：

       给出 N ， K，代表有 N 颗宝石，要求从中选择 K 颗，使等式 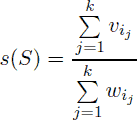  的 S 值达到最大，输出应该选择哪几颗宝石。

 

       思路：

       二分搜索。求 v - s * w >= 0 情况下前 K 个的最大值。二分 S 后，对 v - s * w 由大到小排序即可。double 输入是 %lf。

      

       AC：

#include <cstdio>
#include <algorithm>
#include <cstring>

using namespace std;

typedef struct {
    double v, w, h;
    int num;
}node;

const int INF = 10000005;

node jew[100005];
int n, k;

int cmp(node a, node b) { return a.h > b.h; }

bool C(double s) {
        for (int i = 0 ; i < n; ++i)
                jew[i].h = jew[i].v - s * jew[i].w;

        sort(jew, jew + n, cmp);

        double sum = 0;
        for (int i = 0; i < k; ++i)
                sum += jew[i].h;

        return sum >= 0;
}

void solve() {
        double l = 0, r = INF;

        for (int i = 0; i < 50; ++i) {
                double mid = (l + r) / 2;
                if (C(mid)) l = mid;
                else r = mid;
        }

        for (int i = 0 ; i < k; ++i) {
                printf("%d", jew[i].num);
                i == k - 1 ? printf("\n") : printf(" ");
        }
}

int main () {
        scanf("%d%d", &n, &k);

        for (int i = 0; i < n; ++i) {
                scanf("%lf%lf", &jew[i].v, &jew[i].w);
                jew[i].num = i + 1;
        }

        solve();

        return 0;
}