算法杂货铺——k均值聚类(K-means)（转 ）

4.1、摘要

      在前面的文章中，介绍了三种常见的分类算法。分类作为一种监督学习方法，要求必须事先明确知道各个类别的信息，并且断言所有待分类项都有一个类别与之对应。但是很多时候上述条件得不到满足，尤其是在处理海量数据的时候，如果通过预处理使得数据满足分类算法的要求，则代价非常大，这时候可以考虑使用聚类算法。聚类属于无监督学习，相比于分类，聚类不依赖预定义的类和类标号的训练实例。本文首先介绍聚类的基础——距离与相异度，然后介绍一种常见的聚类算法——k均值和k中心点聚类，最后会举一个实例：应用聚类方法试图解决一个在体育界大家颇具争议的问题——中国男足近几年在亚洲到底处于几流水平。

4.2、相异度计算

      在正式讨论聚类前，我们要先弄清楚一个问题：如何定量计算两个可比较元素间的相异度。用通俗的话说，相异度就是两个东西差别有多大，例如人类与章鱼的相异度明显大于人类与黑猩猩的相异度，这是能我们直观感受到的。但是，计算机没有这种直观感受能力，我们必须对相异度在数学上进行定量定义。

      设，其中X，Y是两个元素项，各自具有n个可度量特征属性，那么X和Y的相异度定义为：，其中R为实数域。也就是说相异度是两个元素对实数域的一个映射，所映射的实数定量表示两个元素的相异度。

      下面介绍不同类型变量相异度计算方法。

4.2.1、标量

      标量也就是无方向意义的数字，也叫标度变量。现在先考虑元素的所有特征属性都是标量的情况。例如，计算X={2,1,102}和Y={1,3,2}的相异度。一种很自然的想法是用两者的欧几里得距离来作为相异度，欧几里得距离的定义如下：

      

      其意义就是两个元素在欧氏空间中的集合距离，因为其直观易懂且可解释性强，被广泛用于标识两个标量元素的相异度。将上面两个示例数据代入公式，可得两者的欧氏距离为：

      

      除欧氏距离外，常用作度量标量相异度的还有曼哈顿距离和闵可夫斯基距离，两者定义如下：

      曼哈顿距离：

      闵可夫斯基距离：

      欧氏距离和曼哈顿距离可以看做是闵可夫斯基距离在p=2和p=1下的特例。另外这三种距离都可以加权，这个很容易理解，不再赘述。

      下面要说一下标量的规格化问题。上面这样计算相异度的方式有一点问题，就是取值范围大的属性对距离的影响高于取值范围小的属性。例如上述例子中第三个属性的取值跨度远大于前两个，这样不利于真实反映真实的相异度，为了解决这个问题，一般要对属性值进行规格化。所谓规格化就是将各个属性值按比例映射到相同的取值区间，这样是为了平衡各个属性对距离的影响。通常将各个属性均映射到[0,1]区间，映射公式为：

      

      其中max(ai)和min(ai)表示所有元素项中第i个属性的最大值和最小值。例如，将示例中的元素规格化到[0,1]区间后，就变成了X’={1,0,1}，Y’={0,1,0}，重新计算欧氏距离约为1.732。

4.2.2、二元变量

      所谓二元变量是只能取0和1两种值变量，有点类似布尔值，通常用来标识是或不是这种二值属性。对于二元变量，上一节提到的距离不能很好标识其相异度，我们需要一种更适合的标识。一种常用的方法是用元素相同序位同值属性的比例来标识其相异度。

      设有X={1,0,0,0,1,0,1,1}，Y={0,0,0,1,1,1,1,1}，可以看到，两个元素第2、3、5、7和8个属性取值相同，而第1、4和6个取值不同，那么相异度可以标识为3/8=0.375。一般的，对于二元变量，相异度可用“取值不同的同位属性数/单个元素的属性位数”标识。

      上面所说的相异度应该叫做对称二元相异度。现实中还有一种情况，就是我们只关心两者都取1的情况，而认为两者都取0的属性并不意味着两者更相似。例如在根据病情对病人聚类时，如果两个人都患有肺癌，我们认为两个人增强了相似度，但如果两个人都没患肺癌，并不觉得这加强了两人的相似性，在这种情况下，改用“取值不同的同位属性数/(单个元素的属性位数-同取0的位数)”来标识相异度，这叫做非对称二元相异度。如果用1减去非对称二元相异度，则得到非对称二元相似度，也叫Jaccard系数，是一个非常重要的概念。

4.2.3、分类变量

      分类变量是二元变量的推广，类似于程序中的枚举变量，但各个值没有数字或序数意义，如颜色、民族等等，对于分类变量，用“取值不同的同位属性数/单个元素的全部属性数”来标识其相异度。

4.2.4、序数变量

      序数变量是具有序数意义的分类变量，通常可以按照一定顺序意义排列，如冠军、亚军和季军。对于序数变量，一般为每个值分配一个数，叫做这个值的秩，然后以秩代替原值当做标量属性计算相异度。

4.2.5、向量

      对于向量，由于它不仅有大小而且有方向，所以闵可夫斯基距离不是度量其相异度的好办法，一种流行的做法是用两个向量的余弦度量，其度量公式为：

      

      其中||X||表示X的欧几里得范数。要注意，余弦度量度量的不是两者的相异度，而是相似度！

4.3、聚类问题

      在讨论完了相异度计算的问题，就可以正式定义聚类问题了。

      所谓聚类问题，就是给定一个元素集合D，其中每个元素具有n个可观察属性，使用某种算法将D划分成k个子集，要求每个子集内部的元素之间相异度尽可能低，而不同子集的元素相异度尽可能高。其中每个子集叫做一个簇。

      与分类不同，分类是示例式学习，要求分类前明确各个类别，并断言每个元素映射到一个类别，而聚类是观察式学习，在聚类前可以不知道类别甚至不给定类别数量，是无监督学习的一种。目前聚类广泛应用于统计学、生物学、数据库技术和市场营销等领域，相应的算法也非常的多。本文仅介绍一种最简单的聚类算法——k均值（k-means）算法。

4.4、K-means算法及其示例

      k均值算法的计算过程非常直观：

      1、从D中随机取k个元素，作为k个簇的各自的中心。

      2、分别计算剩下的元素到k个簇中心的相异度，将这些元素分别划归到相异度最低的簇。

      3、根据聚类结果，重新计算k个簇各自的中心，计算方法是取簇中所有元素各自维度的算术平均数。

      4、将D中全部元素按照新的中心重新聚类。

      5、重复第4步，直到聚类结果不再变化。

      6、将结果输出。

      由于算法比较直观，没有什么可以过多讲解的。下面，我们来看看k-means算法一个有趣的应用示例：中国男足近几年到底在亚洲处于几流水平？

      今年中国男足可算是杯具到家了，几乎到了过街老鼠人人喊打的地步。对于目前中国男足在亚洲的地位，各方也是各执一词，有人说中国男足亚洲二流，有人说三流，还有人说根本不入流，更有人说其实不比日韩差多少，是亚洲一流。既然争论不能解决问题，我们就让数据告诉我们结果吧。

      下图是我采集的亚洲15只球队在2005年-2010年间大型杯赛的战绩（由于澳大利亚是后来加入亚足联的，所以这里没有收录）。

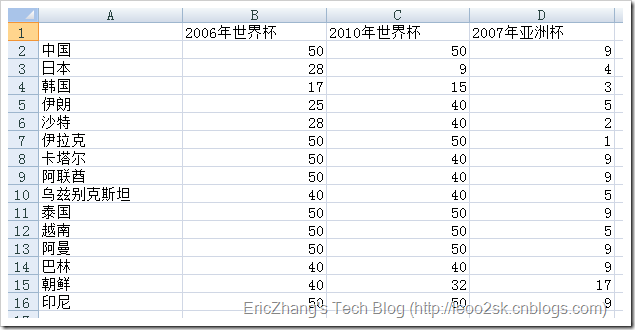
      其中包括两次世界杯和一次亚洲杯。我提前对数据做了如下预处理：对于世界杯，进入决赛圈则取其最终排名，没有进入决赛圈的，打入预选赛十强赛赋予40，预选赛小组未出线的赋予50。对于亚洲杯，前四名取其排名，八强赋予5，十六强赋予9，预选赛没出现的赋予17。这样做是为了使得所有数据变为标量，便于后续聚类。

      下面先对数据进行[0,1]规格化，下面是规格化后的数据：

      接着用k-means算法进行聚类。设k=3，即将这15支球队分成三个集团。

      现抽取日本、巴林和泰国的值作为三个簇的种子，即初始化三个簇的中心为A：{0.3, 0, 0.19}，B：{0.7, 0.76, 0.5}和C：{1, 1, 0.5}。下面，计算所有球队分别对三个中心点的相异度，这里以欧氏距离度量。下面是我用程序求取的结果：

      从做到右依次表示各支球队到当前中心点的欧氏距离，将每支球队分到最近的簇，可对各支球队做如下聚类：

      中国C，日本A，韩国A，伊朗A，沙特A，伊拉克C，卡塔尔C，阿联酋C，乌兹别克斯坦B，泰国C，越南C，阿曼C，巴林B，朝鲜B，印尼C。

      第一次聚类结果：

      A：日本，韩国，伊朗，沙特；

      B：乌兹别克斯坦，巴林，朝鲜；

      C：中国，伊拉克，卡塔尔，阿联酋，泰国，越南，阿曼，印尼。

      下面根据第一次聚类结果，调整各个簇的中心点。

      A簇的新中心点为：{(0.3+0+0.24+0.3)/4=0.21, (0+0.15+0.76+0.76)/4=0.4175, (0.19+0.13+0.25+0.06)/4=0.1575} = {0.21, 0.4175, 0.1575}

      用同样的方法计算得到B和C簇的新中心点分别为{0.7, 0.7333, 0.4167}，{1, 0.94, 0.40625}。

      用调整后的中心点再次进行聚类，得到：

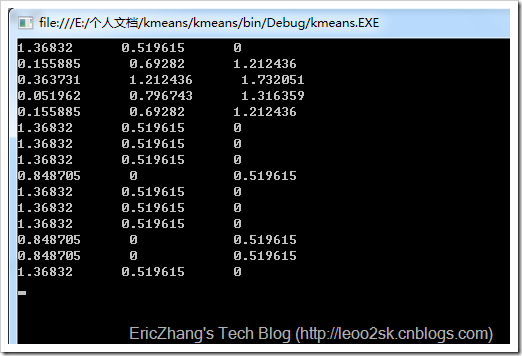
      第二次迭代后的结果为：

      中国C，日本A，韩国A，伊朗A，沙特A，伊拉克C，卡塔尔C，阿联酋C，乌兹别克斯坦B，泰国C，越南C，阿曼C，巴林B，朝鲜B，印尼C。

      结果无变化，说明结果已收敛，于是给出最终聚类结果：

      亚洲一流：日本，韩国，伊朗，沙特

      亚洲二流：乌兹别克斯坦，巴林，朝鲜

      亚洲三流：中国，伊拉克，卡塔尔，阿联酋，泰国，越南，阿曼，印尼

      看来数据告诉我们，说国足近几年处在亚洲三流水平真的是没有冤枉他们，至少从国际杯赛战绩是这样的。

      其实上面的分析数据不仅告诉了我们聚类信息，还提供了一些其它有趣的信息，例如从中可以定量分析出各个球队之间的差距，例如，在亚洲一流队伍中，日本与沙特水平最接近，而伊朗则相距他们较远，这也和近几年伊朗没落的实际相符。另外，乌兹别克斯坦和巴林虽然没有打进近两届世界杯，不过凭借预算赛和亚洲杯上的出色表现占据B组一席之地，而朝鲜由于打入了2010世界杯决赛圈而有幸进入B组，可是同样奇迹般夺得2007年亚洲杯的伊拉克却被分在三流，看来亚洲杯冠军的分量还不如打进世界杯决赛圈重啊。其它有趣的信息，有兴趣的朋友可以进一步挖掘。

 

大家可以加我个人微信号：scccdgf

 

更多：http://blog.csdn.net/wbj01100