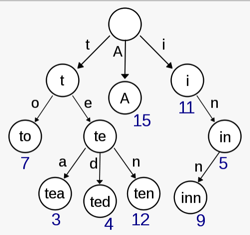
TrieцаСя╝МхПИхПлхБЪхЙНч╝АцаСцИЦшАЕцШпхнЧхЕ╕цаСя╝МцШпф╕АчзНцЬЙх║ПчЪДцаСуАВф╗Очй║хнЧчмжф╕▓чЪДца╣х╝АхзЛя╝Мх╛Аф╕ЛщБНхОЖхИ░цЯРф╕кшКВчВ╣я╝МчбохоЪф║Жхп╣х║ФчЪДхнЧчмжф╕▓я╝Мф╣Ях░▒цШпшп┤я╝Мф╗╗цДПф╕Аф╕кшКВчВ╣чЪДцЙАцЬЙхнРхнЩщГ╜хЕ╖хдЗчЫ╕хРМчЪДхЙНч╝АуАВцпПф╕Ацг╡TrieцаСщГ╜хПпф╗ешвлчЬЛхБЪцШпф╕Аф╕кчоАхНХчЙИчЪДчбохоЪцЬЙщЩРчК╢цАБчЪДшЗкхКицЬ║я╝ИDFAя╝Мdeterministic finite automatonя╝Йя╝Мф╣Ях░▒цШпшп┤я╝Мхп╣ф║Оф╕Аф╕кф╗╗цДПч╗ЩхоЪчЪДх▒Юф║ОшпешЗкхКицЬ║чЪДчК╢цАБ(тСа)хТМф╕Аф╕кх▒Юф║ОшпешЗкхКицЬ║хнЧцпНшбичЪДхнЧчмж(тСб)я╝МщГ╜хПпф╗еца╣цНоч╗ЩхоЪчЪДш╜мчз╗хЗ╜цХ░(тСв)ш╜мхИ░ф╕Лф╕Аф╕кчК╢цАБхО╗уАВхЕ╢ф╕ня╝Ъ
- тСа хп╣ф║ОTrieцаСф╕нчЪДцпПф╕Аф╕кшКВчВ╣щГ╜чбохоЪф║Жф╕Аф╕кшЗкхКицЬ║чЪДчК╢цАБя╝Ы
- тСб ч╗ЩхоЪф╕Аф╕кх▒Юф║ОшпешЗкхКицЬ║хнЧцпНшбичЪДхнЧчмжя╝МхЬихЫ╛ф╕нхПпф╗ечЬЛхИ░ца╣цНоф╕НхРМчЪДхнЧчмжх╜вцИРчЪДхИЖцФпя╝Ы
- тСв ф╗Ох╜УхЙНшКВчВ╣ш┐ЫхЕеф╕Лф╕Ах▒ВцмбшКВчВ╣чЪДш┐ЗчиЛч╗Пш┐ЗчК╢цАБш╜мчз╗хЗ╜цХ░х╛ЧхЗ║уАВ
ф╕Аф╕кщЭЮх╕╕х╕╕шзБчЪДх║ФчФих░▒цШпцРЬч┤вцПРчд║я╝МхЬицРЬч┤вцбЖф╕нш╛УхЕецРЬч┤вф┐бцБпчЪДхЙНч╝Ая╝МхжВтАЬф╣Мщ▓БтАЭя╝МцПРчд║тАЬф╣Мщ▓БцЬищ╜РтАЭя╝ЫхЖНцЬЙх░▒цШпш╛УхЕец│ХчЪДшБФцГ│хКЯшГ╜я╝Мф╣ЯцШпф╕Аца╖чЪДщБУчРЖуАВ
хТМф║МхПЙцРЬч┤вцаСя╝Иbinary search treeя╝ЙчЫ╕цпФ
ф║МхПЙцРЬч┤вцаСхПИхПлхБЪф║МхПЙцОТх║ПцаСя╝МхоГц╗бш╢│я╝Ъ
- ф╗╗цДПшКВчВ╣хжВцЮЬх╖жхнРцаСф╕Нф╕║чй║я╝Мх╖жхнРцаСцЙАцЬЙшКВчВ╣чЪДхА╝щГ╜х░Пф║Оца╣шКВчВ╣чЪДхА╝я╝Ы
- ф╗╗цДПшКВчВ╣хжВцЮЬхП│хнРцаСф╕Нф╕║чй║я╝МхП│хнРцаСцЙАцЬЙшКВчВ╣чЪДхА╝щГ╜хдзф║Оца╣шКВчВ╣чЪДхА╝я╝Ы
- х╖жхП│хнРцаСф╣ЯщГ╜цШпф║МхПЙцРЬч┤вцаСя╝Ы
- цЙАцЬЙшКВчВ╣чЪДхА╝щГ╜ф╕НчЫ╕хРМуАВ
хЕ╢хоЮф║МхПЙцРЬч┤вцаСчЪДф╝ШхК┐х╖▓ч╗ПхЬиф╕ОцЯецЙ╛уАБцПТхЕечЪДцЧ╢щЧ┤хдНцЭВх║жф╕Кф║Жя╝МщАЪх╕╕хПкцЬЙO(log n)я╝Мх╛ИхдЪщЫЖхРИщГ╜цШпщАЪш┐ЗхоГцЭехоЮчО░чЪДуАВхЬиш┐ЫшбМцПТхЕечЪДцЧ╢хАЩя╝МхоЮш┤иф╕КцШпч╗ЩцаСц╖╗хКацЦ░чЪДхП╢хнРшКВчВ╣я╝МщБ┐хЕНф║ЖшКВчВ╣чз╗хКия╝МцРЬч┤вуАБцПТхЕехТМхИащЩдчЪДхдНцЭВх║жчнЙф║ОцаСчЪДщлШх║жя╝Мх▒Юф║ОO(log n)я╝МцЬАхЭПцГЕхЖ╡ф╕ЛцХ┤цг╡цаСцЙАцЬЙчЪДшКВчВ╣щГ╜хПкцЬЙф╕Аф╕кхнРшКВчВ╣я╝МхоМхЕихПШцИРф╕Аф╕кч║┐цАзшбия╝МхдНцЭВх║жцШпO(n)уАВ
TrieцаСхЬицЬАхЭПцГЕхЖ╡ф╕ЛцЯецЙ╛шжБх┐лш┐Зф║МхПЙцРЬч┤вцаСя╝МхжВцЮЬцРЬч┤вхнЧчмжф╕▓щХ┐х║жчФиmцЭешбичд║чЪДшпЭя╝МхоГхПкцЬЙO(m)я╝МщАЪх╕╕цГЕхЖ╡я╝ИцаСчЪДшКВчВ╣ф╕кцХ░шжБш┐Ьхдзф║ОцРЬч┤вхнЧчмжф╕▓чЪДщХ┐х║жя╝Йф╕ЛшжБш┐Ьх░Пф║ОO(n)уАВ
цИСф╗мч╗ЩTrieцаСф╕╛ф╛ЛхнРщГ╜цШпцЛ┐хнЧчмжф╕▓ф╕╛ф╛ЛчЪДя╝МхЕ╢хоЮхоГцЬмш║лхп╣keyчЪДщАВхоЬцАзцШпцЬЙф╕еца╝шжБц▒ВчЪДя╝МхжВцЮЬkeyцШпц╡очВ╣цХ░чЪДшпЭя╝Мх░▒хПпшГ╜хп╝шЗ┤цХ┤ф╕кTrieцаСх╖ищХ┐цЧацпФя╝МшКВчВ╣хПпшп╗цАзф╣ЯщЭЮх╕╕х╖оя╝Мш┐ЩчзНцГЕхЖ╡ф╕ЛцШпф╕НщАВхоЬчФиTrieцаСцЭеф┐ЭхнШцХ░цНочЪДя╝ЫшАМф║МхПЙцРЬч┤вцаСх░▒ф╕НхнШхЬиш┐Щф╕кщЧощвШуАВ
хТМHashшбичЫ╕цпФ
шАГшЩСф╕Аф╕ЛHashшбищФохЖ▓чкБчЪДщЧощвШуАВHashшбищАЪх╕╕цИСф╗мшп┤хоГчЪДхдНцЭВх║жцШпO(1)я╝МхЕ╢хоЮф╕еца╝шп┤ш╡╖цЭеш┐ЩцШпцОеш┐СхоМч╛ОчЪДHashшбичЪДхдНцЭВх║жя╝МхПжхдЦш┐ШщЬАшжБшАГшЩСхИ░hashхЗ╜цХ░цЬмш║лщЬАшжБщБНхОЖцРЬч┤вхнЧчмжф╕▓я╝МхдНцЭВх║жцШпO(m)уАВхЬиф╕НхРМщФошвлцШах░ДхИ░тАЬхРМф╕Аф╕кф╜Нч╜отАЭя╝ИшАГшЩСclosed hashingя╝Мш┐ЩтАЬхРМф╕Аф╕кф╜Нч╜отАЭхПпф╗ечФ▒ф╕Аф╕кцЩощАЪщУ╛шбицЭехПЦф╗гя╝ЙчЪДцЧ╢хАЩя╝МщЬАшжБш┐ЫшбМцЯецЙ╛чЪДхдНцЭВх║жхПЦхЖ│ф║Ош┐ЩтАЬхРМф╕Аф╕кф╜Нч╜отАЭф╕ЛшКВчВ╣чЪДцХ░чЫоя╝МхЫацндя╝МхЬицЬАхЭПцГЕхЖ╡ф╕Ля╝МHashшбиф╣ЯцШпхПпф╗ецИРф╕║ф╕Ах╝ахНХхРСщУ╛шбичЪДя╝Ихп╣ф║ОHashхЖ▓чкБщЧощвШя╝Мшп╖щШЕшп╗уАКHash Collision DoSщЧощвШуАЛя╝ЙуАВ
TrieцаСхПпф╗ецпФш╛ГцЦ╣ф╛┐хЬ░цМЙчЕзkeyчЪДхнЧцпНх║ПцЭецОТх║Пя╝ИцХ┤цг╡цаСхЕИх║ПщБНхОЖф╕Ацмбх░▒хе╜ф║Жя╝Йя╝Мш┐ЩцШпч╗ЭхдзхдЪцХ░HashшбицШпф╕НхРМчЪДя╝ИHashшбиф╕АшИмхп╣ф║Оф╕НхРМчЪДkeyцЭешп┤цШпцЧах║ПчЪДя╝ЙуАВ
хЬиш╛ГчРЖцГ│чЪДцГЕхЖ╡ф╕Ля╝МHashшбихПпф╗еф╗еO(1)чЪДщАЯх║жш┐ЕщАЯхС╜ф╕нчЫоцаЗя╝МхжВцЮЬш┐Щх╝ашбищЭЮх╕╕хдзя╝МщЬАшжБцФ╛хИ░чгБчЫШф╕КчЪДшпЭя╝МHashшбичЪДцЯецЙ╛шо┐щЧохЬичРЖцГ│цГЕхЖ╡ф╕ЛхПкщЬАшжБф╕АцмбхН│хПпя╝Ыф╜ЖцШпTrieцаСшо┐щЧочгБчЫШчЪДцХ░чЫощЬАшжБчнЙф║ОшКВчВ╣ц╖▒х║жуАВ
х╛ИхдЪцЧ╢хАЩTrieцаСцпФHashшбищЬАшжБцЫ┤хдЪчЪДчй║щЧ┤я╝МцИСф╗мшАГшЩСш┐ЩчзНф╕Аф╕кшКВчВ╣хнШцФ╛ф╕Аф╕кхнЧчмжчЪДцГЕхЖ╡чЪДшпЭя╝МхЬиф┐ЭхнШф╕Аф╕кхнЧчмжф╕▓чЪДцЧ╢хАЩя╝Мц▓бцЬЙхКЮц│ХцККхоГф┐ЭхнШцИРф╕Аф╕кхНХчЛмчЪДхЭЧуАВTrieцаСчЪДшКВчВ╣хОЛч╝йхПпф╗ецШОцШ╛ч╝Ушзгш┐Щф╕кщЧощвШя╝МхРОщЭвф╝Ъшо▓хИ░уАВ
хТМхРОч╝АцаСчЫ╕цпФ
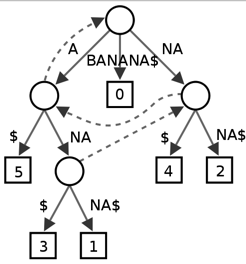
хРОч╝АцаСхОЛч╝йхнШхВиф║Жф╕Ацо╡цЦЗцЬмчЪДцЙАцЬЙхПпшГ╜чЪДхРОч╝Ая╝МхжВч╗ЩхоЪхНХшпНтАЬbananaтАЭя╝МхПпшГ╜чЪДхРОч╝АхМЕцЛмя╝ЪaуАБnaуАБanaуАБnanaуАБananaуАБbananaш┐ЩхЗачзНя╝Мф╕КхЫ╛х╖▓ч╗Пх░ЖцЙАцЬЙхПпшГ╜хЕищГицФ╛хЬицаСф╕ншбичд║хЗ║цЭеф║Жя╝МтАЬ$тАЭшбичд║ф╕Аф╕кхРОч╝АчЪДч╗УцЭЯя╝МхРМцЧ╢я╝Мш┐ШхБЪхИ░ф║Жх░╜щЗПчЪДхИЖцФпхОЛч╝йя╝ИхИЖцФпхОЛч╝йчЪДшп┤цШОхЬиф╕ЛцЦЗф╕нф╣ЯцЬЙцПРхПКя╝ЙуАВхп╣ф║Оч╗ЩхоЪщХ┐х║жф╕║nчЪДцЦЗцЬмцЮДщАахРОч╝АцаСя╝МхоГчЪДхоЪф╣ЙшжБчВ╣хМЕцЛмя╝Ъ
- цаСцЬЙnф╕кхП╢хнРшКВчВ╣я╝МхИЖхИлф╗О1хИ░nцЭехС╜хРНя╝Ы
- щЩдф║Жца╣шКВчВ╣я╝МцЙАцЬЙчЪДщЭЮхП╢хнРшКВчВ╣шЗ│х░СцЬЙф╕дф╕кхнйхнРя╝Ы
- цпПф╕АцЭбш╛╣ф╗гшбихОЯцЦЗцЬмчЪДф╕Аф╕кщЭЮчй║хнРф╕▓я╝Ы
- ф╕НхнШхЬиф╕дцЭбш╛╣ф╗ехРМф╕Аф╕кхнЧчмжх╝Аф╕▓цаЗшо░ф╕Фф╗ехРМф╕Аф╕кхнЧчмжч╗Ух░╛я╝Ы
- хЬиф╗Оца╣шКВчВ╣хИ░хП╢хнР i чЪДш╖пх╛Дф╕Кя╝Мш┐ЮцОецЙАцЬЙхнЧчмжф╕▓цаЗшо░х╜вцИРчЪДхнЧчмжф╕▓я╝МщГ╜шбичд║ф║Жф╕Аф╕кхОЯцЦЗцЬмчЪДхРОч╝АхнРф╕▓уАВ
┬а
цЮДщАахРОч╝АцаСца╣цНоцЦЗцЬмщХ┐х║жщЬАшжБц╢ИшАЧч║┐цАзчЪДцЧ╢щЧ┤уАВхТМTrieцаСчЫ╕цпФя╝МхРОч╝АцаСхБЪхИ░ф║ЖчФичй║щЧ┤цНвцЧ╢щЧ┤я╝МшАГшЩСхЕицЦЗцРЬч┤вчЪДцГЕхЖ╡я╝МхРОч╝АцаСцККцЙАцЬЙхПпшГ╜чЪДхРОч╝АхнРф╕▓щГ╜ч┤вх╝ХхМЦф║Жя╝Мх░▒щБ┐хЕНф║ЖTrieцаСц╖▒х║жщБНхОЖцХ┤цг╡цаСчЪДш┐ЗчиЛуАВхЬичоЧц│ХщвШф╕ншо╕хдЪхЕ│ф║ОтАЬхЙНч╝АхнРф╕▓тАЭщЧощвШф╕Кя╝МцИСф╗мч╗Пх╕╕ф╜┐чФиTrieцаСцЭец▒Вшзгя╝Мф╜ЖцШпхжВцЮЬщЧощвШф╗Еф╗Ец╢ЙхПКтАЬхнРф╕▓тАЭя╝Мх╛Ах╛АщАЙчФихРОч╝АцаСя╝ЫхПжхдЦя╝Мш┐ШцЬЙф╕Аф╕кщЗНшжБчЪДф╜┐чФихЬицЦЗцЬмхОЛч╝йчоЧц│Хф╕Кя╝МщАЪш┐ЗхРОч╝АцаСхПпф╗ецЙ╛хИ░щЗНхдНчОЗщлШчЪДцЦЗцЬмя╝МхоЮчО░щЗНхдНцЦЗцЬмцК╜хПЦя╝МцФ╛хИ░хнЧхЕ╕цШах░Дшбиф╕нхО╗уАВ
TrieцаСчЪДцФ╣ш┐Ы
1. цМЙф╜НTrieцаСя╝ИBitwise Trieя╝Йя╝ЪхОЯчРЖф╕КхТМцЩощАЪTrieцаСх╖оф╕НхдЪя╝МхПкф╕Нш┐ЗцЩощАЪTrieцаСхнШхВичЪДцЬАх░ПхНХф╜НцШпхнЧчмжя╝Мф╜ЖцШпBitwise TrieхнШцФ╛чЪДцШпф╜НшАМх╖▓уАВф╜НцХ░цНочЪДхнШхПЦчФ▒CPUцМЗф╗дф╕АцмбчЫ┤цОехоЮчО░я╝Мхп╣ф║Оф║Мш┐ЫхИ╢цХ░цНоя╝МхоГчРЖшо║ф╕КшжБцпФцЩощАЪTrieцаСх┐луАВ
2. шКВчВ╣хОЛч╝йуАВ
- тСа хИЖцФпхОЛч╝йя╝Ъхп╣ф║Очи│хоЪчЪДTrieцаСя╝МхЯ║цЬмф╕КщГ╜цШпцЯецЙ╛хТМшп╗хПЦцУНф╜Ья╝МхоМхЕихПпф╗ецККф╕Аф║ЫхИЖцФпш┐ЫшбМхОЛч╝йуАВф╛ЛхжВя╝МхЙНхЫ╛ф╕нцЬАхП│ф╛зхИЖцФпчЪДinnхПпф╗ечЫ┤цОехОЛч╝йцИРф╕Аф╕кшКВчВ╣тАЬinnтАЭя╝МшАМф╕НщЬАшжБф╜Ьф╕║ф╕Ацг╡х╕╕шзДчЪДхнРцаСхнШхЬиуАВRadixцаСх░▒цШпца╣цНош┐Щф╕кхОЯчРЖцЭешзгхЖ│TrieцаСш┐Зц╖▒щЧощвШчЪДуАВ
- тСб шКВчВ╣цШах░Дшбия╝Ъш┐ЩчзНцЦ╣х╝Пф╣ЯцШпхЬиTrieцаСчЪДшКВчВ╣хПпшГ╜х╖▓ч╗ПхЗаф╣ОхоМхЕичбохоЪчЪДцГЕхЖ╡ф╕ЛщЗЗчФичЪДя╝МщТИхп╣TrieцаСф╕ншКВчВ╣чЪДцпПф╕Аф╕кчК╢цАБя╝МхжВцЮЬчК╢цАБцА╗цХ░щЗНхдНх╛ИхдЪчЪДшпЭя╝МщАЪш┐Зф╕Аф╕кхЕГч┤аф╕║цХ░хнЧчЪДхдЪч╗┤цХ░ч╗Дя╝ИцпФхжВTriple Array Trieя╝ЙцЭешбичд║я╝Мш┐Щца╖хнШхВиTrieцаСцЬмш║лчЪДчй║щЧ┤х╝АщФАф╝Ъх░Пф╕Аф║Ыя╝МшЩ╜шп┤х╝ХхЕеф║Жф╕Ах╝ащвЭхдЦчЪДцШах░ДшбиуАВ
цЦЗчлач│╗цЬмф║║хОЯхИЫя╝Мш╜мш╜╜шп╖ф┐ЭцМБхоМцХ┤цАзх╣╢ц│ицШОхЗ║шЗкуАКхЫЫчБлчЪДхФахПиуАЛ










чЫ╕хЕ│цОишНР
хнЧхЕ╕цаСя╝Мф╣Яшвлчз░ф╕║TrieцаСцИЦхЙНч╝АцаСя╝МцШпф╕АчзНщлШцХИчЪДцХ░цНоч╗УцЮДя╝Мх░дхЕ╢щАВчФиф║ОхнЧчмжф╕▓чЫ╕хЕ│чЪДцЯецЙ╛хТМцПТхЕецУНф╜ЬуАВхЬишобчоЧцЬ║чзСхнжщвЖхЯЯя╝МхоГшвлх╣┐ц│Ых║ФчФихЬихнЧхЕ╕уАБцРЬч┤вх╝ХцУОуАБшЗкхКишбехЕихКЯшГ╜ф╗ехПКIPш╖пчФ▒чнЙцЦ╣щЭвуАВTrieцаСчЪДца╕х┐Гф╝ШхК┐хЬиф║ОхЕ╢шГ╜хдЯщАЪш┐З...
TrieцаСя╝Мф╣Яшвлчз░ф╕║хЙНч╝АцаСцИЦхнЧхЕ╕цаСя╝МцШпф╕АчзНцХ░цНоч╗УцЮДя╝Мф╕╗шжБчФиф║ОщлШцХИхЬ░хнШхВихТМцгАч┤вхнЧчмжф╕▓уАВхЬиTrieцаСф╕ня╝МцпПф╕кшКВчВ╣ф╗гшбиф╕Аф╕кхнЧчмжф╕▓чЪДхЙНч╝Ая╝МшАМф╗Оца╣шКВчВ╣хИ░цЯРф╕кшКВчВ╣чЪДш╖пх╛Дф╕КчЪДш╛╣ф╗гшбиф║Жш┐Щф╕кшКВчВ╣цЙАф╗гшбичЪДхнЧчмжф╕▓уАВш┐ЩчзНч╗УцЮДчЙ╣хИлщАВхРИ...
чЫ╕хп╣цЭешп┤я╝МTrieцаСцШпф╕АчзНцпФш╛ГчоАхНХчЪДцХ░цНоч╗УцЮДуАВчРЖшзгш╡╖цЭецпФш╛ГчоАхНХя╝Мф╜ЖцШпчоАхНХчЪДф╕Ьше┐ф╣Ях╛Чф╗ШхЗ║ф╗гф╗╖уАВцХЕTrieцаСф╣ЯцЬЙхоГчЪДч╝║чВ╣я╝МTrieцаСчЪДхЖЕхнШц╢ИшАЧщЭЮх╕╕хдзуАВ TrieцаСчЪДхЯ║цЬмцАзш┤ихПпф╗ех╜Тч║│ф╕║я╝Ъ 1. ца╣шКВчВ╣ф╕НхМЕхРлхнЧчмжя╝МщЩдца╣шКВчВ╣хдЦцпП...
**цХ░цНоч╗УцЮДхоЮщкМцКехСКтАФтАФTrieцаС** TrieцаСя╝МхПИчз░ф╕║хЙНч╝АцаСцИЦхнЧхЕ╕цаСя╝МцШпф╕АчзНчФиф║ОхнШхВихнЧчмжф╕▓чЪДцЬЙцХИцХ░цНоч╗УцЮДуАВхоГщАЪш┐Зх░ЖхнЧчмжф╕▓чЪДхнЧчмжхИЖшзгх╣╢хнШхВихЬицаСчЪДшКВчВ╣ф╕ня╝МцЭехоЮчО░щлШцХИчЪДхнЧчмжф╕▓цЯецЙ╛уАБцПТхЕехТМхИащЩдцУНф╜ЬуАВхЬиTrieцаСф╕ня╝МцпПф╕к...
### ITчмФшпХщЭвшпХ--TrieцаС...TrieцаСцШпф╕АчзНщЭЮх╕╕щЗНшжБчЪДцХ░цНоч╗УцЮДя╝МхЬиф┐бцБпцгАч┤вуАБхнЧчмжф╕▓хМ╣щЕНчнЙщвЖхЯЯцЬЙчЭАх╣┐ц│ЫчЪДх║ФчФия╝МхРМцЧ╢ф╣ЯцШпх╛ИхдЪчоЧц│ХхТМхдНцЭВцХ░цНоч╗УцЮДчЪДхЯ║чбАуАВцОМцПбTrieцаСф╕Нф╗ЕцЬЙхКйф║ОшзгхЖ│хоЮщЩЕщЧощвШя╝Мф╣ЯшГ╜цПРхНЗф╕кф║║хЬиITщвЖхЯЯчЪДчлЮф║ЙхКЫуАВ
хЬиш┐Щф╕кшп╛шо╛ф╕ня╝М`file.cpp`х╛ИхПпшГ╜цШпхоЮчО░TrieцаСцХ░цНоч╗УцЮДхПКхЕ╢цУНф╜ЬчЪДц║Рф╗гчаБцЦЗф╗╢уАВхПпшГ╜хМЕцЛмцПТхЕехНХшпНуАБхИащЩдхНХшпНуАБцЯецЙ╛хНХшпНуАБцШ╛чд║цЙАцЬЙф╗ечЙ╣хоЪхЙНч╝Ах╝Ахд┤чЪДхНХшпНчнЙхКЯшГ╜уАВC++цШпхоЮчО░ш┐Щч▒╗чоЧц│ХчЪДх╕╕чФич╝ЦчиЛшпншиАя╝МхоГцПРф╛Ыф║Жф╕░хпМчЪДцОзхИ╢...
TrieцаСя╝Мф╣Ячз░ф╕║хЙНч╝АцаСцИЦхнЧхЕ╕цаСя╝МцШпф╕АчзНчФиф║ОхнШхВихнЧчмжф╕▓цХ░цНоч╗УцЮДуАВхоГхИйчФихнЧчмжф╕▓щЧ┤чЪДхЕмхЕ▒хЙНч╝АцЭехЗПх░СцЙАщЬАчЪДхнШхВичй║щЧ┤я╝Мф╜┐х╛ЧцЯецЙ╛хнЧчмжф╕▓цЫ┤хКащлШцХИуАВTrieцаСхЬих╛ИхдЪх║ФчФиф╕нщГ╜цЬЙх╣┐ц│ЫчЪДх║ФчФия╝МхжВцЛ╝хЖЩцгАцЯеуАБшЗкхКишбехЕихКЯшГ╜чнЙуАВ #### ...
чФиCхоЮчО░чЪДцХ░цНоч╗УцЮДTrieцаСчоЧц│Х хоЮщкМчЪДхЗ╜цХ░чЪДtrieцаСчЪДцПТхЕе цРЬч┤вхТМхИащЩд
ч╗╝ф╕КцЙАш┐░я╝МщАЪш┐ЗTrieцаСцХ░цНоч╗УцЮДхТМJavaч╝ЦчиЛя╝МцИСф╗мхПпф╗ецЮДх╗║ф╕Аф╕кщлШцХИчЪДцРЬч┤вцПРчд║ч│╗ч╗Яя╝МцибцЛЯш░╖цнМхТМчЩ╛х║жчЪДцРЬч┤вф╜УщкМуАВш┐Щц╢ЙхПКхИ░TrieцаСчЪДцПТхЕехТМцЯецЙ╛цУНф╜Ья╝Мф╗ехПКф╕ОчФицИ╖чХМщЭвф║дф║ТчЪДщА╗ш╛СхдДчРЖуАВхЬихоЮщЩЕх╝АхПСф╕ня╝МцИСф╗мш┐ШщЬАшжБхЕ│ц│ицАзшГ╜ф╝ШхМЦ...
TrieцаСя╝МхПИчз░ф╕║хнЧхЕ╕цаСя╝МцШпф╕АчзНчЙ╣цоКчЪДцаСх╜вцХ░цНоч╗УцЮДя╝Мф╕╗шжБчФиф║ОщлШцХИхЬ░хнШхВихТМцгАч┤вхнЧчмжф╕▓уАВхоГчЪДшо╛шобчЫочЪДцШпщАЪш┐ЗхИйчФихнЧчмжф╕▓чЪДхЕмхЕ▒хЙНч╝АцЭехЗПх░СхнЧчмжф╕▓цпФш╛ГчЪДцмбцХ░я╝Мф╗ОшАМцПРщлШцЯешпвцХИчОЗуАВTrieцаСчЪДца╕х┐ГчЙ╣чВ╣цШпя╝Ъ 1. ца╣шКВчВ╣ф╕НхМЕхРл...
**хУИх╕М Trie цаСя╝ИHashTrieя╝Йф╕ОхнЧхЕ╕цаСя╝ИTrieцаСя╝Йшпжшзг** хУИх╕М Trie цаСя╝Мф╣Ячз░ф╕║ HashTrie цИЦшАЕцШпхУИх╕МхМЦчЪД Trie цаСя╝МцШпф╕АчзНч╗УхРИф║ЖхУИх╕МшбихТМ Trie цХ░цНоч╗УцЮДчЙ╣чВ╣чЪДцХ░цНоч╗УцЮДуАВхоГхЬи Trie цаСчЪДхЯ║чбАф╕Кх╝ХхЕеф║ЖхУИх╕МхЗ╜цХ░я╝МцПРщлШф║Ж...
**TrieцаС**я╝МхПИчз░ф╕║**хнЧхЕ╕цаС**цИЦ**хЙНч╝АцаС**я╝МцШпф╕АчзНчФиф║ОщлШцХИхнШхВихТМцгАч┤вхнЧчмжф╕▓чЪДцаСх╜вцХ░цНоч╗УцЮДуАВхоГщАЪш┐ЗхИйчФихнЧчмжф╕▓ф╣ЛщЧ┤чЪДхЕмхЕ▒хЙНч╝АцЭехЗПх░СцЯешпвцЧ╢щЧ┤я╝Мф╗ОшАМцПРщлШцРЬч┤вцХИчОЗуАВхЬишп╕хжВцЦЗцЬмч╝Цш╛СхЩиуАБцРЬч┤вх╝ХцУОуАБшЗкхКишбехЕичнЙхКЯшГ╜ф╕нщЭЮх╕╕...
чоЧц│ХхоЮчО░я╝МC++хоЮчО░trieцаСя╝МхоМцИРшпечоЧц│ХчЪДхоЮчО░я╝Мш┐РчФиш┐РчФи
цА╗ч╗Уя╝МDoubleArrayTrieцШпф╕АчзНщлШцХИчЪДхнЧчмжф╕▓цЯецЙ╛цХ░цНоч╗УцЮДя╝МхоГчЪДшо╛шобхТМхоЮчО░ч╗УхРИф║ЖTrieцаСчЪДчЙ╣цАзх╣╢ш┐ЫшбМф║Жф╝ШхМЦя╝МщАВчФиф║ОщЬАшжБх┐лщАЯхдДчРЖхдзщЗПхнЧчмжф╕▓чЪДхЬ║цЩпуАВхЬихоЮщЩЕх║ФчФиф╕ня╝Мф║ЖшзгхТМцОМцПбDATчЪДхОЯчРЖхТМф╜┐чФицЦ╣ц│Хя╝Мхп╣ф║ОцПРхНЗхнЧчмжф╕▓хдДчРЖчЪД...
Trie цаСя╝Мф╣Ячз░ф╕║хнЧхЕ╕цаСя╝МцШпф╕АчзНцаСх╜вцХ░цНоч╗УцЮДя╝МчФиф║ОщлШцХИхнШхВихТМцЯешпвхнЧчмжф╕▓уАВхЕ╢ца╕х┐ГцАЭцГ│цШпчй║щЧ┤цНвцЧ╢щЧ┤я╝МхН│щАЪш┐ЗхНачФицЫ┤хдЪчЪДхнШхВичй║щЧ┤цЭецНвхПЦцЯешпвщАЯх║жчЪДцПРщлШуАВ Trie цаСчЪДхЯ║цЬмч╗УцЮДцШпф╕Аф╕кшКВчВ╣цХ░ч╗Дя╝МцпПф╕кшКВчВ╣хп╣х║Фф╕Аф╕кхнЧчмжя╝Мф╗Оца╣...
TrieцаСцШпф╕АчзНчФиф║ОщлШцХИхнШхВихТМцгАч┤вхнЧчмжф╕▓цХ░цНочЪДцХ░цНоч╗УцЮДя╝МчЙ╣хИлщАВчФиф║ОцЮДх╗║шпНхЕ╕уАВхп╣ф║Оч╗ЩхоЪчЪДхнЧчмжф╕▓╬▒1, ╬▒2, тАж, ╬▒nя╝МхЬиTrieцаСф╕нцРЬч┤вцЬАхдЪхПкщЬАшжБч╗Пш┐ЗnцмбхМ╣щЕНхН│хПпхоМцИРф╕АцмбцЯецЙ╛я╝Мш┐Щф╜┐х╛ЧхоГцИРф╕║ф╕нцЦЗхМ╣щЕНхИЖшпНчоЧц│Хф╕ншпНхЕ╕чЪДф╕АчзН...
ACM TrieцаС цибцЭ┐,хнЧхЕ╕цаСцибцЭ┐я╝МцХ░цНоч╗УцЮД
TrieцаСя╝МхПИчз░хнЧхЕ╕цаСцИЦхЙНч╝АцаСя╝МцШпф╕АчзНчФиф║ОщлШцХИхнШхВихТМцгАч┤вхнЧчмжф╕▓чЪДцХ░цНоч╗УцЮДуАВхоГчЪДф╕╗шжБчЙ╣чВ╣цШпшГ╜хдЯх┐лщАЯцЯецЙ╛ф╕Аф╕кхнЧчмжф╕▓цШпхРжцШпхПжф╕Аф╕кхнЧчмжф╕▓чЪДхЙНч╝Ая╝Мш┐Щхп╣ф║ОхдДчРЖхдзщЗПхнЧчмжф╕▓чЪДщЧощвШщЭЮх╕╕цЬЙчФиуАВхЬищвШчЫоцППш┐░ф╕нцПРхИ░чЪДPOJ1056уАБPOJ...
хЬишобчоЧцЬ║чзСхнжщвЖхЯЯя╝МTrieцаСя╝ИхПИчз░хЙНч╝АцаСцИЦхнЧхЕ╕цаСя╝ЙцШпф╕АчзНчФиф║ОхнШхВихЕ╖цЬЙхЕ▒хРМхЙНч╝АчЪДхнЧчмжф╕▓чЪДщлШцХИцХ░цНоч╗УцЮДуАВхоГх╣┐ц│Ых║ФчФиф║ОхРДчзНхЬ║цЩпя╝МхжВшЗкхКишбехЕиуАБцЛ╝хЖЩцгАцЯеф╗ехПКIPш╖пчФ▒шбичнЙуАВцЬмцЦЗх░Жшпжч╗Жф╗Лч╗НхжВф╜ХхЬиC/C++ф╕нхоЮчО░ф╕Аф╕кхЯ║цЬмчЪДTrie...