1 дЇМеИЖжЯ•жЙЊ/жКШеНКжЯ•жЙЊ
жАЭжГ≥пЉЪеЬ®жЬЙеЇПжХ∞зїДдЄ≠жЯ•жЙЊжЯРдЄАзЙєеЃЪеЕГзі†зЪДжРЬ糥зЃЧж≥ХгАВжРЬзі†ињЗз®ЛдїОжХ∞зїДзЪДдЄ≠йЧіеЕГзі†еЉАеІЛпЉМе¶ВжЮЬдЄ≠йЧіеЕГзі†ж≠£е•љжШѓи¶БжЯ•жЙЊзЪДеЕГзі†пЉМеИЩжРЬзі†ињЗз®ЛзїУжЭЯпЉЫе¶ВжЮЬжЯРдЄАзЙєеЃЪеЕГзі†е§ІдЇОжИЦиАЕе∞ПдЇОдЄ≠йЧіеЕГзі†пЉМеИЩеЬ®жХ∞зїДе§ІдЇОжИЦе∞ПдЇОдЄ≠йЧіеЕГзі†зЪДйВ£дЄАеНКдЄ≠жЯ•жЙЊпЉМиАМдЄФиЈЯеЉАеІЛдЄАж†ЈдїОдЄ≠йЧіеЕГзі†еЉАеІЛжѓФиЊГгАВ
жЧґйЧіе§НжЭВеЇ¶пЉЪжКШеНКжРЬ糥жѓПжђ°жККжРЬ糥еМЇеЯЯеЗПе∞СдЄАеНКпЉМжЧґйЧіе§НжЭВеЇ¶дЄЇ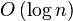 жИЦlog2(n)гАВпЉИж≥®жДПlog2(n)еТМlog(n)еЕґеЃЮжШѓеРМж†ЈзЪДе§НжЭВеЇ¶пЉМеЫ†дЄЇеЃГдїђдєЛйЧідїЕдїЕеЈЃдЇЖдЄАдЄ™еЄЄйЗПз≥їжХ∞иАМеЈ≤пЉЙгАВпЉИnдї£и°®йЫЖеРИдЄ≠еЕГзі†зЪДдЄ™жХ∞пЉЙ
жИЦlog2(n)гАВпЉИж≥®жДПlog2(n)еТМlog(n)еЕґеЃЮжШѓеРМж†ЈзЪДе§НжЭВеЇ¶пЉМеЫ†дЄЇеЃГдїђдєЛйЧідїЕдїЕеЈЃдЇЖдЄАдЄ™еЄЄйЗПз≥їжХ∞иАМеЈ≤пЉЙгАВпЉИnдї£и°®йЫЖеРИдЄ≠еЕГзі†зЪДдЄ™жХ∞пЉЙ
з©ЇйЧіе§НжЭВеЇ¶пЉЪ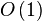 гАВиЩљдї•йАТељТ嚥еЉПеЃЪдєЙпЉМдљЖжШѓе∞ЊйАТељТпЉМеПѓжФєеЖЩдЄЇеЊ™зОѓгАВ
гАВиЩљдї•йАТељТ嚥еЉПеЃЪдєЙпЉМдљЖжШѓе∞ЊйАТељТпЉМеПѓжФєеЖЩдЄЇеЊ™зОѓгАВ
йАВзФ®иМГеЫіпЉЪдЉШзВєжШѓжѓФиЊГжђ°жХ∞е∞СпЉМжЯ•жЙЊйАЯеЇ¶ењЂпЉМеє≥еЭЗжАІиГље•љпЉЫеЕґзЉЇзВєжШѓи¶Бж±ВеЊЕжЯ•и°®дЄЇжЬЙеЇПи°®пЉМдЄФжПТеЕ•еИ†йЩ§еЫ∞йЪЊгАВеЫ†ж≠§пЉМжКШеНКжЯ•жЙЊжЦєж≥ХйАВзФ®дЇОдЄНзїПеЄЄеПШеК®иАМжЯ•жЙЊйҐСзєБзЪДжЬЙеЇПеИЧи°®гАВ
жЬАе§ЪжЬАе∞СпЉЪеЕГзі†жЬЙеЇПжЧґжКШеНКжЯ•жЙЊпЉЪжЬАе§Ъ![]() +1жђ°пЉМжЬАе∞С1жђ°пЉЫеЕГзі†жЧ†еЇПеП™иГљй°ЇеЇПжЯ•жЙЊпЉЪжЬАе§Ъnжђ°пЉМжЬАе∞С1жђ°
+1жђ°пЉМжЬАе∞С1жђ°пЉЫеЕГзі†жЧ†еЇПеП™иГљй°ЇеЇПжЯ•жЙЊпЉЪжЬАе§Ъnжђ°пЉМжЬАе∞С1жђ°
public class BinarySearch {
/**
* дЇМеИЖжЯ•жЙЊзЃЧж≥ХпЉМйЭЮйАТељТ
*
* @param srcArray жЬЙеЇПжХ∞зїД
* @param des жЯ•жЙЊеЕГзі†
* @return desзЪДжХ∞зїДдЄЛж†ЗпЉМж≤°жЙЊеИ∞ињФеЫЮ-1
*/
public static int binarySearch(int[] srcArray, int des)
{
int low = 0;
int high = srcArray.length-1;
while(low <= high)
{
int middle = (low + high)/2;
if(des == srcArray[middle])
{
return middle;
}
else if(des <srcArray[middle])
{
high = middle - 1;
}
else
{
low = middle + 1;
}
}
return -1;
}
public static void main(String[] args)
{
int[] src = new int[] {1, 3, 5, 7, 8, 9};
System.out.println(binarySearch(src, 3));
}
}
 
//жКШеНКжЯ•жЙЊйАТељТзЃЧж≥Х
//жߕ胥жИРеКЯињФеЫЮиѓ•еѓєи±°зЪДдЄЛж†ЗеЇПеПЈпЉМ姱賕жЧґињФеЫЮ-1гАВ
int BiSearch2(int r[],int low,int high,int k)
{
if(low>high)
return -1;
else
{
int mid=(low+high)/2;
if(r[mid]==k)
return mid;
else
if(r[mid]<k)
return BiSearch2(r,mid+1,high,k);
else
return BiSearch2(r,low,mid-1,k);
}
}
 
public static void main(String[] args) {
int r[]={1,2,3,4,5};
System.out.println(BiSearch2(r,1,5,5));
}
 
еПВиАГпЉЪhttp://zh.wikipedia.org/wiki/%E6%8A%98%E5%8D%8A%E6%90%9C%E7%B4%A2%E7%AE%97%E6%B3%95
http://www.2cto.com/kf/201212/172713.html
2 дЇМеПЙжОТеЇПж†С
¬†еПИзІ∞дЇМеПЙжЯ•жЙЊ(жРЬ糥)ж†С(Binary Search Tree)гАВеЕґеЃЪдєЙдЄЇпЉЪдЇМеПЙжОТеЇПж†СжИЦиАЕжШѓз©Їж†СпЉМжИЦиАЕжШѓжї°иґ≥е¶ВдЄЛжАІиі®зЪДдЇМеПЙж†СпЉЪ
вС†иЛ•еЃГзЪДеЈ¶е≠Рж†СйЭЮз©ЇпЉМеИЩеЈ¶е≠Рж†СдЄКжЙАжЬЙзїУзВєзЪДеАЉеЭЗе∞ПдЇОж†єзїУзВєзЪДеАЉпЉЫвС°иЛ•еЃГзЪДеП≥е≠Рж†СйЭЮз©ЇпЉМеИЩеП≥е≠Рж†СдЄКжЙАжЬЙзїУзВєзЪДеАЉеЭЗе§ІдЇОж†єзїУзВєзЪДеАЉпЉЫ
вСҐеЈ¶гАБеП≥е≠Рж†СжЬђиЇЂеПИеРДжШѓдЄАж£µдЇМеПЙжОТеЇПж†СгАВ







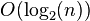



зЫЄеЕ≥жО®иНР
4. **ж†єжЯ•жЙЊзЃЧж≥Х**пЉЪеѓїжЙЊеЗљжХ∞зЪДйЫґзВєпЉМе¶ВдЇМеИЖж≥ХгАБзЙЫй°њ-жЛЙеЉЧж£Ѓж≥Хз≠ЙгАВињЩдЇЫжЦєж≥ХеЬ®иІ£еЖ≥жЦєз®Лж±ВиІ£йЧЃйҐШжЧґйЭЮеЄЄжЬЙзФ®пЉМJavaеПѓдї•йАЪињЗињ≠дї£еЃЮзО∞гАВ 5. **дЉШеМЦзЃЧж≥Х**пЉЪе¶В楃寶дЄЛйЩНж≥ХгАБзЙЫй°њж≥ХгАБйБЧдЉ†зЃЧж≥Хз≠ЙпЉМзФ®дЇОжЙЊеИ∞еЗљжХ∞зЪДжЬАе∞ПеАЉжИЦ...
гАКJavaеЄЄзФ®зЃЧж≥ХжЙЛеЖМгАЛжШѓдЄАжЬђйЭҐеРСJavaеИЭе≠¶иАЕзЪДзЃЧж≥ХжМЗеНЧпЉМжЧ®еЬ®йАЪињЗжЈ±еЕ•жµЕеЗЇзЪДжЦєеЉПпЉМеЄЃеК©иѓїиАЕзРЖиІ£еєґжОМжП°еРДзІНеЄЄиІБзЪДзЉЦз®ЛзЃЧж≥ХпЉМдїОиАМжПРйЂШдїЦдїђзЪДзЉЦз®ЛиГљеКЫеТМиІ£еЖ≥йЧЃйҐШзЪДжХИзОЗгАВињЩжЬђдє¶зЪДи¶ЖзЫЦиМГеЫіеєњж≥ЫпЉМжґЙеПКеИ∞зЃЧж≥ХеЯЇз°АгАБжХ∞жНЃзїУжЮД...
8. **ж†єжЯ•жЙЊзЃЧж≥Х**пЉЪжѓФе¶ВдЇМеИЖжЯ•жЙЊж≥ХгАБSecantжЦєж≥ХеТМBrentжЦєж≥ХпЉМзФ®дЇОеѓїжЙЊеЗљжХ∞зЪДеЃЮж†єжИЦе§Нж†єгАВ 9. **жХ∞еАЉзІѓеИЖ**пЉЪе¶ВиЊЫжЩЃж£Ѓж≥ХеИЩгАБ楃嚥ж≥ХеИЩеТМйЂШжЦѓзІѓеИЖпЉМеЃГдїђзФ®дЇОдЉ∞иЃ°еЗљжХ∞зЪДзІѓеИЖеАЉпЉМзЙєеИЂйАВеРИе§ДзРЖдЄНиІДеИЩеИЖеЄГзЪДжХ∞жНЃгАВ 10. *...
ињЩдЄ™"JavaеЄЄзФ®жХ∞еАЉзЃЧж≥ХйЫЖ"еПѓиГљеМЕеРЂдЇЖдї•дЄКжПРеИ∞зЪДдЄАдЇЫзЃЧж≥ХзЪДеЃЮзО∞пЉМйАЪињЗе≠¶дє†еТМз†Фз©ґињЩдЇЫдї£з†БпЉМеЉАеПСиАЕдЄНдїЕеПѓдї•еК†жЈ±еѓєжХ∞еАЉзЃЧж≥ХзЪДзРЖиІ£пЉМињШиГљжПРйЂШиІ£еЖ≥йЧЃйҐШзЪДиГљеКЫгАВиЃ∞еЊЧеЬ®еЃЮйЩЕдљњзФ®жЧґпЉМж†єжНЃеЕЈдљУйЬАж±ВйАЙжЛ©еРИйАВзЪДзЃЧж≥ХеТМеЇУпЉМеєґдЉШеМЦ...
8. **ж†єжЯ•жЙЊзЃЧж≥Х**пЉЪе¶ВдЇМеИЖжЯ•жЙЊж≥ХгАБзЙЫй°њ-жЛЙеЉЧж£Ѓж≥ХгАБSecantжЦєж≥Хз≠ЙпЉМзФ®дЇОеѓїжЙЊжЦєз®ЛзЪДеЃЮж†єгАВињЩдЇЫеЬ®зЙ©зРЖж®°еЮЛж±ВиІ£гАБжОІеИґзРЖиЃЇз≠ЙйҐЖеЯЯйГљжЬЙеЇФзФ®гАВ 9. **еВЕзЂЛеПґеПШжНҐ**пЉЪз¶їжХ£еВЕзЂЛеПґеПШжНҐпЉИDFTпЉЙеТМењЂйАЯеВЕзЂЛеПґеПШжНҐпЉИFFTпЉЙжШѓе§ДзРЖ...
6. **жОТеЇПдЄОжЯ•жЙЊзЃЧж≥Х**пЉЪењЂйАЯжОТеЇПгАБељТеєґжОТеЇПгАБдЇМеИЖжЯ•жЙЊз≠ЙпЉМиЩљзДґдЄНжШѓдЄУйЧ®зЪДжХ∞еАЉзЃЧж≥ХпЉМдљЖеЃГдїђеЬ®е§ДзРЖжХ∞жНЃжЧґиЗ≥еЕ≥йЗНи¶БгАВ 7. **жХ∞еАЉз®≥еЃЪжАІеТМиѓѓеЈЃеИЖжЮР**пЉЪзРЖиІ£зЃЧж≥ХзЪДиѓѓеЈЃжЭ•жЇРеТМе¶ВдљХдњЭжМБиЃ°зЃЧзїУжЮЬзЪДз≤ЊеЇ¶пЉМжШѓжХ∞еАЉиЃ°зЃЧдЄ≠зЪДж†ЄењГ...
гАКJavaеЄЄзФ®зЃЧж≥ХжЙЛеЖМгАЛжШѓдЄАжЬђжЈ±еЕ•жОҐиЃ®JavaзЉЦз®ЛдЄ≠еЄЄиІБзЃЧж≥ХзЪДеЃЮзФ®жМЗеНЧпЉМжЧ®еЬ®еЄЃеК©еЉАеПСиАЕжПРеНЗеЬ®еЃЮйЩЕеЈ•дљЬдЄ≠иІ£еЖ≥е§НжЭВйЧЃйҐШзЪДиГљеКЫгАВињЩжЬђдє¶жґµзЫЦдЇЖдїОеЯЇз°АеИ∞йЂШзЇІзЪДеРДзІНзЃЧж≥ХпЉМдЄЇJavaз®ЛеЇПеСШжПРдЊЫдЇЖдЄ∞еѓМзЪДе≠¶дє†иµДжЇРгАВ й¶ЦеЕИпЉМжЬђдє¶дЉЪ...
гАКJavaеЄЄзФ®зЃЧж≥ХжЙЛеЖМгАЛеИЖдЄЙзѓЗпЉМеЕ±13зЂ†пЉМеИЖеИЂдїЛзїНдЇЖзЃЧж≥ХеЯЇз°АгАБзЃЧж≥ХеЇФзФ®еТМзЃЧж≥ХйЭҐиѓХйҐШгАВй¶ЦеЕИдїЛзїНдЇЖзЃЧж≥Хж¶Вињ∞пЉМзДґеРОйЗНзВєеИЖжЮРдЇЖжХ∞жНЃзїУжЮДеТМеЯЇжЬђзЃЧж≥ХжАЭжГ≥пЉЫжО•зЭАпЉМиѓ¶зїЖиЃ≤иІ£дЇЖзЃЧж≥ХеЬ®жОТеЇПгАБжЯ•жЙЊгАБжХ∞е≠¶иЃ°зЃЧгАБжХ∞иЃЇгАБеОЖеП≤иґ£йҐШгАБжЄЄжИП...
жЬђиµДжЇРвАЬJavaеЄЄзФ®жХ∞еАЉзЃЧж≥ХйЫЖвАЭжПРдЊЫдЇЖдЄ∞еѓМзЪДзЃЧж≥ХеЃЮзО∞пЉМеЄЃеК©еЉАеПСиАЕжПРйЂШз®ЛеЇПзЪДиЃ°зЃЧжХИзОЗеТМз≤ЊеЇ¶гАВдї•дЄЛжШѓж†єжНЃж†ЗйҐШгАБжППињ∞еТМж†Зз≠ЊжПРзВЉеЗЇзЪДдЄАдЇЫйЗНи¶БJavaжХ∞еАЉзЃЧж≥ХзЯ•иѓЖзВєпЉЪ 1. **еЯЇз°АзЃЧж≥Х**пЉЪJavaдЄ≠зЪДеЯЇжЬђзЃЧжЬѓињРзЃЧеМЕжЛђеК†еЗПдєШйЩ§...
гАКJavaеЄЄзФ®зЃЧж≥ХжЙЛеЖМгАЛжЇРдї£з†БжШѓдЄАдїљйЭЮеЄЄеЃЭиіµзЪДиµДжЇРпЉМеЃГдЄЇJavaеЉАеПСиАЕжПРдЊЫдЇЖдЄ∞еѓМзЪДзЃЧж≥ХеЃЮзО∞пЉМжШѓе≠¶дє†еТМеЃЮиЈµзЃЧж≥ХзЪДзРЖжГ≥жЭРжЦЩгАВињЩдїљжЇРдї£з†БйЫЖеРИжґµзЫЦдЇЖе§ЪзІНзїПеЕЄеТМеЃЮзФ®зЪДзЃЧж≥ХпЉМжЧ®еЬ®еЄЃеК©еЉАеПСиАЕжПРеНЗзЉЦз®ЛжКАиГљпЉМзРЖиІ£зЃЧж≥ХеОЯзРЖпЉМеєґиГљ...
2. **жЯ•жЙЊзЃЧж≥Х**пЉЪе¶ВдЇМеИЖжЯ•жЙЊгАБеУИеЄМжЯ•жЙЊгАБзЇњжАІжЯ•жЙЊз≠ЙгАВдЇМеИЖжЯ•жЙЊеЬ®жЬЙеЇПжХ∞зїДдЄ≠еЕЈжЬЙдЉШзІАзЪДжЯ•жЙЊжХИзОЗпЉМеУИеЄМжЯ•жЙЊеИЩеИ©зФ®еУИеЄМи°®еЃЮзО∞ињСдєОеН≥жЧґзЪДжЯ•жЙЊгАВ 3. **еЫЊиЃЇзЃЧж≥Х**пЉЪе¶ВжЈ±еЇ¶дЉШеЕИжРЬ糥пЉИDFSпЉЙеТМеєњеЇ¶дЉШеЕИжРЬ糥пЉИBFSпЉЙпЉМдї•еПК...
ж†єжНЃжПРдЊЫзЪДжЦЗдїґдњ°жБѓпЉМвАЬJavaеЄЄзФ®зЃЧж≥ХжЙЛеЖМ.pdfвАЭдЉЉдєОжШѓдЄАдїљйТИеѓєJavaз®ЛеЇПеСШзЪДе≠¶дє†иµДжЇРпЉМжЧ®еЬ®еЄЃеК©дїЦдїђжОМжП°еТМжПРеНЗеЬ®зЃЧж≥ХжЦєйЭҐзЪДзЯ•иѓЖдЄОжКАиГљгАВзДґиАМпЉМеЯЇдЇОжПРдЊЫзЪДзЃАзЯ≠жППињ∞еТМйГ®еИЖеЖЕеЃєжЭ•зЬЛпЉМеєґж≤°жЬЙзЫіжО•жґЙеПКеЕЈдљУзЪДзЃЧж≥ХзЯ•иѓЖзВєпЉМ...
2. жЯ•жЙЊзЃЧж≥ХпЉЪ - зЇњжАІжЯ•жЙЊпЉЪйБНеОЖжХідЄ™жХ∞зїДпЉМзЫіеИ∞жЙЊеИ∞зЫЃж†ЗеЕГзі†жИЦйБНеОЖзїУжЭЯгАВ - дЇМеИЖжЯ•жЙЊпЉЪйАВзФ®дЇОжЬЙеЇПжХ∞зїДпЉМжѓПжђ°е∞ЖжЯ•жЙЊиМГеЫіеЗПеНКпЉМжПРйЂШжХИзОЗгАВ - еУИеЄМжЯ•жЙЊпЉЪйАЪињЗеУИеЄМеЗљжХ∞ењЂйАЯеЃЪдљНеЕГзі†пЉМдљЖеПѓиГљжЬЙеУИеЄМеЖ≤з™БйЧЃйҐШгАВ 3. жХ∞жНЃ...
гАКJavaеЄЄзФ®зЃЧж≥ХжЙЛеЖМгАЛжШѓдЄАжЬђжЈ±еЕ•жµЕеЗЇзЪДзЉЦз®ЛиµДжЇРпЉМдЄїи¶БжґµзЫЦдЇЖJavaзЉЦз®Лиѓ≠и®АдЄ≠зЪДеРДзІНеЄЄиІБзЃЧж≥ХпЉМеѓєдЇОе≠¶дє†еТМжПРеНЗJavaзЉЦз®ЛжКАеЈІдї•еПКзРЖиІ£зЃЧж≥ХжАЭжГ≥еЕЈжЬЙйЗНи¶БдїЈеАЉгАВињЩдїљжЙЛеЖМдї•еЃЮйЩЕеПѓињРи°МзЪДдї£з†БдЄЇиљљдљУпЉМдљњиѓїиАЕиГље§ЯзЫіиІВеЬ∞зЬЛеИ∞зЃЧж≥Х...