说起排序,大多数人在实际项目中很少自己去写一个排序,一般来说,qsort一行话就可以了。我也很少在实际项目中用到过基数排序,最近,写了一篇博客文章叫做: 字符串之全文索引 ,这篇文章的下一篇文章 要用到一个倍增算法。这个倍增算法,就可以非常巧妙的运用基数排序。作为那篇文章的一个铺垫,我专门写了一篇基数排序的文章。这篇文章里面的基数排序肯定是一个变形。
大多数网上 或者 书上的基数排序都是从下面的例子开始的:
排序下面的数列:
73 22 93 43 55 14 28 65 39 81
然后对这些数字,用个位数进行排序:
| 0 | |||||||||
| 1 | 81 | ||||||||
| 2 | 22 | ||||||||
| 3 | 73 | 93 | 43 | ||||||
| 4 | 14 | ||||||||
| 5 | 55 | 65 | |||||||
| 6 | |||||||||
| 7 | |||||||||
| 8 | 28 | ||||||||
| 9 | 39 |
从这个二维的数组里面顺序取出:
81 22 73 93 43 14 55 65 28 39
再对10位数进行排序:
| 0 | |||||||||
| 1 | 14 | ||||||||
| 2 | 22 | 28 | |||||||
| 3 | 39 | ||||||||
| 4 | 43 | ||||||||
| 5 | 55 | 65 | |||||||
| 6 | |||||||||
| 7 | 73 | ||||||||
| 8 | 81 | ||||||||
| 9 | 93 |
从这个二维数组里面顺序取出:
14 22 28 39 43 55 65 73 81 93
上面的思路写成代码也非常的容易写:
#include <stdio.h>
#include <stdlib.h>
int main()
{
int data[10]={73,22,93,43,55,14,28,65,39,81};
int temp[10][10]= {0};
int order[10]={0};
int i,j,k,n,lsd;
printf("\n排序前: ");
for (i=0; i<10; i++) printf("%d ",data[i]);
putchar('\n');
n=1;
while (n<=10)
{
for (i=0;i<10;i++)
{
lsd=((data[i]/n)%10);
temp[lsd][order[lsd]]=data[i];
order[lsd]++;
}
printf("\n重新排列: ");
k = 0;
for (i=0;i<10;i++)
{
if(order[i]!=0)
{
for (j=0;j<order[i];j++)
{
data[k]=temp[i][j];
printf("%d ",data[k]);
k++;
}
order[i]=0;
}
}
n *= 10;
}
putchar('\n');
printf("\n排序后: ");
for (i=0; i<10; i++) printf("%d ",data[i]);
return 0;
}
既然这个基数排序理论上性能比较的高,这样的话,我们就写个程序比较一下实际上快速排序和基数排序的速度。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>
#include <algorithm>
#define MAX_N 5000000
int sort[10][MAX_N];
int data[MAX_N];
int data2[MAX_N];
int data3[MAX_N];
int radix_sort(int data[], int max_index, int max_number);
static int range_rand(int min, int max);
int intcmp(const void *a, const void *b)
{
return *((int *)a) - *((int *)b);
}
int main()
{
int i;
int max = -1;
clock_t t;
for (i = 0; i < MAX_N; i++)
{
data[i] = range_rand(1, 0xFFFFFFF);
if (max < data[i]) max = data[i];
}
memcpy(data2, data, sizeof(data));
memcpy(data3, data, sizeof(data));
t = clock();
qsort(data, MAX_N, sizeof(int), intcmp);
printf("qsort cost : %d \n", clock() - t);
t = clock();
radix_sort(data2, MAX_N, max);
printf("radix cost : %d \n", clock() - t);
t = clock();
std::sort(data3, data3 + MAX_N);
printf("std::sort cost : %d \n", clock() - t);
for (i = 0; i < 20; i++)
{
printf("%d ", data[i]);
}
printf("\n");
for (i = 0; i < 20; i++)
{
printf("%d ", data2[i]);
}
printf("\n");
for (i = 0; i < 20; i++)
{
printf("%d ", data3[i]);
}
printf("\n");
}
int radix_sort(int data[], int max_index, int max_number)
{
int number[10];
int lsd, i, k, j, n;
n = 1;
memset(number, 0, sizeof(number));
while (n <= max_number)
{
for (i = 0; i < max_index; i++)
{
lsd = (data[i]/n) % 10;
sort[lsd][number[lsd]] = data[i];
number[lsd]++;
}
k = 0;
for (i = 0; i < 10; i++)
{
if(number[i] != 0)
{
for (j = 0; j < number[i];j++)
{
data[k] = sort[i][j];
k++;
}
number[i] = 0;
}
}
n *= 10;
}
return 0;
}
static int range_rand(int min, int max)
{
double r = 0;
int i;
double mul = 1;
for (i = 0; i < 3; i++)
{
mul *= 0.0001;
r += (rand() % 10000) * mul;
}
//0 - 1 中的一个随机数
return (int)(r * (max - min)) + min;
}
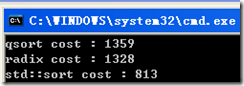
我用了500万数据进行测试,在我电脑上的运行结果是:
你会发现C++ stl 里面的sort 是最快的(没有函数调用的损失)。radix sort 和 qsort 性能差不多。所以,在某个数字可能很大的时候,上面的这个算法没有任何性能上的优势,还会浪费非常多的内存。
基数排序大多数情况下面只适用于下面的情景,一组数,这组数的最大值不是很大,更加准确的说,是要排序的对象的数目 和 排序对象的最大值之间相差不多。比如,这组数 1 4 5 2 2,要排序对象的数目是 5 ,排序对象的最大值也是 5. 这样的情况很适合。我们原来的排序的数,默认是以10为基数,现在,这个改进算法是这样的,我以最大的那个数为基数,这样,所有的数都是“个位数”,问题就简单了。
说了这样多,我觉得还是用程序来表达比较的清晰:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>
#include <algorithm>
#define MAX_N 5000000
int sort[10][MAX_N];
int quick_radix_sort[MAX_N];
int data[MAX_N];
int data2[MAX_N];
int data3[MAX_N];
int data4[MAX_N];
int qradix_sort(int data[], int max_index);
int radix_sort(int data[], int max_index, int max_number);
static int range_rand(int min, int max);
int intcmp(const void *a, const void *b)
{
return *((int *)a) - *((int *)b);
}
int main()
{
int i;
int max = -1;
clock_t t;
//初始化随机数种子
srand ( time(NULL) );
for (i = 0; i < MAX_N; i++)
{
data[i] = range_rand(1, MAX_N - 1);
if (max < data[i]) max = data[i];
}
memcpy(data2, data, sizeof(data));
memcpy(data3, data, sizeof(data));
memcpy(data4, data, sizeof(data));
t = clock();
qsort(data, MAX_N, sizeof(int), intcmp);
printf("qsort cost : %d \n", clock() - t);
t = clock();
radix_sort(data2, MAX_N, max);
printf("radix cost : %d \n", clock() - t);
t = clock();
std::sort(data3, data3 + MAX_N);
printf("std::sort cost : %d \n", clock() - t);
t = clock();
qradix_sort(data4, MAX_N);
printf("quick radix sort cost : %d \n", clock() - t);
for (i = 0; i < 20; i++)
{
printf("%d ", data[i]);
}
printf("\n");
for (i = 0; i < 20; i++)
{
printf("%d ", data2[i]);
}
printf("\n");
for (i = 0; i < 20; i++)
{
printf("%d ", data3[i]);
}
printf("\n");
for (i = 0; i < 20; i++)
{
printf("%d ", data4[i]);
}
printf("\n");
}
int qradix_sort(int data[], int max_index)
{
int i, j, n = 0;
for (i = 0; i < max_index; i++)
{
quick_radix_sort[data[i]]++;
}
for (i = 0; i < max_index; i++)
{
for (j = 0; j < quick_radix_sort[i]; j++)
{
data[n++] = i;
}
}
return 0;
}
int radix_sort(int data[], int max_index, int max_number)
{
int number[10];
int lsd, i, k, j, n;
n = 1;
memset(number, 0, sizeof(number));
while (n <= max_number)
{
for (i = 0; i < max_index; i++)
{
lsd = (data[i]/n) % 10;
sort[lsd][number[lsd]] = data[i];
number[lsd]++;
}
k = 0;
for (i = 0; i < 10; i++)
{
if(number[i] != 0)
{
for (j = 0; j < number[i];j++)
{
data[k] = sort[i][j];
k++;
}
number[i] = 0;
}
}
n *= 10;
}
return 0;
}
static int range_rand(int min, int max)
{
double r = 0;
int i;
double mul = 1;
for (i = 0; i < 3; i++)
{
mul *= 0.0001;
r += (rand() % 10000) * mul;
}
//0 - 1 中的一个随机数
return (int)(r * (max - min)) + min;
}
这个代码其实就是在上面的测试代码的基础上加上了一个qradix_sort 函数,这个函数非常的简单:
int qradix_sort(int data[], int max_index)
{
int i, j, n = 0;
for (i = 0; i < max_index; i++)
{
quick_radix_sort[data[i]]++;
}
for (i = 0; i < max_index; i++)
{
for (j = 0; j < quick_radix_sort[i]; j++)
{
data[n++] = i;
}
}
return 0;
}
循环体里面就两句话,和我们前面的那个基数排序不是很一样,这里,已经不用一个二维数组保存排序的数字了,只是标记一下这个数字有几个,因为,下标其实就是被排序的数字。
重新排序这个循环也很简单,仔细冥想一下怎么回事,不懂就在草稿纸上画画草图吧。这里主要的思想还是,下标就是排序的数字。
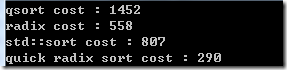
最后的排序测试结果:
我们发现,现在普通的radix性能也提高了,因为,现在数字变小了,循环的次数也变少了。快速基数排序的性能提高还是非常的明显。普通基数排序的两倍,std::sort 的3倍,qsort的 5倍,最重要的是代码非常的简单,基本上是你见过的最简单的一个排序了。
对一个真正的程序员来说,很少这样要死抠一个程序的性能,一般情况下,也是得不偿失。只有,在某个东西真正成了一个性能瓶颈的时候,我们才需要去关心一下:是不是可以这样改进一下。
这个排序算法,将来会应用到 字符串处理的倍增算法里面,这个倍增算法,要反复的进行排序。如果,排序能快一点,这个程序就能快很多。








相关推荐
#### 三、基数排序原理和应用 - **原理**: - 基数排序通过逐位对元素进行排序来完成整体排序的过程。 - 其效率取决于数据的位数和要排序的元素数量,时间复杂度为O(kn),其中k为数字的位数,n为元素数量。 - ...
9. **基数排序**:多关键字的稳定排序算法,通过按低位先排序,然后收集;再按高位排序,然后再收集;依次类推,直到最高位。 10. **桶排序**:基于比较的排序算法,通过将数组分到有限数量的桶里达到排序的效果。 ...
排序算法,如插入排序、选择排序、希尔排序、快速排序、堆排序、归并排序和基数排序,也是考核的重点,要求考生能够比较不同排序算法的性能。 在操作系统部分,考试关注的是对操作系统基本概念、原理的理解,特别是...
8. 排序:了解各种排序算法(插入排序、选择排序、希尔排序、快速排序、堆排序、归并排序、基数排序)的基本思想,但不需深入到算法实现细节。 在操作系统部分,考试着重考察基本概念、设计方法和实现技术。具体...
- 计数排序、桶排序和基数排序:适用于特定类型数据的线性时间排序。 2. **查找算法**: - 线性查找:简单查找,时间复杂度为O(n)。 - 二分查找:适用于有序数组,时间复杂度为O(logn)。 - 哈希查找:通过哈希...
7. 排序算法,包括插入排序、选择排序、希尔排序、快速排序、堆排序、归并排序和基数排序等,以及这些算法的比较。 考试题型及分值比例包括: 1. 填空题,占10分。 2. 单选题,占20分。 3. 简答题,占30分。 4. ...
它通常基于基数排序或者LCP(Longest Common Prefix)的概念,是高级字符串处理技术的一部分。 以上知识点仅仅是ACM竞赛领域冰山一角,它们不仅要求选手具备扎实的数学和计算机科学理论基础,还需要通过大量的实践...
位图联接索引(Bitmap Join Index):位图联接索引是针对多表联接查询优化的,它在一个表上创建位图索引,并将另一个表的值映射到这个位图索引上。在执行联接查询时,可以直接利用位图之间的运算来定位结果集,...
8. 各种排序算法,如插入排序、选择排序、希尔排序、快速排序、堆排序、归并排序和基数排序。 在操作系统部分,大纲侧重于考察学生对操作系统基本概念、原理的理解和应用能力,包括操作系统的设计与实现技术。重点...
7、go ahead - 不对应题目,可能是一个错误或遗漏 以上内容涵盖了日常对话用语、动词短语搭配、词汇变形以及句型构造等多个英语基础知识点,旨在检验五年级学生在日常生活场景中的英语沟通能力和语言运用技能。通过...
- 掌握各种排序算法,如插入排序、简单选择排序、希尔排序、快速排序、堆排序、归并排序和基数排序,分析它们的时间和空间复杂度。 ### 《计算机操作系统》部分 操作系统课程着重于基本概念、原理的理解,设计方法...
- **最小路径覆盖**:在有向图中找到一个路径集合,使得每个顶点至少被一个路径覆盖。 #### 十一、图论—支撑树 - **最小生成树(kruskal邻接表)**:Kruskal算法用于求解加权无向图的最小生成树。 - **最小生成树...
1. 视图:视图是数据库中的虚拟表,它是由SQL查询语句创建的,不存储实际数据,而是从一个或多个基本表中动态生成数据。视图可以简化复杂的查询,提供数据安全性,因为可以限制用户对基础表的直接访问。然而,视图的...
3. **基数排序**:非比较型整数排序算法,根据数字位数进行多次分配与收集,常用于大量整数排序。 **二、高精度计算** 1. **大整数的加、乘、除法**:处理超过普通整型范围的大数运算,如使用链表或数组存储位数,...
1. **数的认识**:在题目中出现的数位概念,例如"5 个亿,24 个万和 375 个一",这是对大数的表示,需要理解不同数位代表的数值,以及如何读写这样的数。 2. **分数比较**:在题目的第2题中,需要比较分数的大小和...