直接看代码吧。嘿嘿~
/*
** File name: LinkPriorityQueue.h
** Author: ZhouFeng
** Date: 2012/03/30
** LPQ -- LinkPriorityQueue
*/
#ifndef LINK_PRIORITY_QUEUE_H
#define LINK_PRIORITY_QUEUE_H
#define ERROR 0
#define SUCCESS 1
#define BOOL int
#define TRUE 1
#define FALSE 0
typedef int EleDataType;
typedef struct EleType
{
EleDataType data;
int nPriority;
}EleType;
typedef struct LPQNode
{
EleType eleData;
struct LPQNode *pNext;
}LPQNode;
typedef struct LinkPriorityQueue
{
int nCount;
struct LPQNode *pRear;
struct LPQNode *pFront;
}LinkPriorityQueue, *PLPQ;
void InitLPQ(PLPQ *pLPQAddr);
BOOL IsLPQEmpty(PLPQ pLPQ);
/* et -- EleType varible. */
int LPQAppend(PLPQ pLPQ, EleType et);
int LPQDelete(PLPQ pLPQ, EleType *et);
int GetLPQ(PLPQ pLPQ, EleType *et);
void FreeLPQ(PLPQ *pLPQ);
#endif
/*
** File name: LinkPriorityQueue.c
** Author: ZhouFeng
** Date: 2012/03/30
** LPQ operation definition.
*/
#include <stddef.h>
#include <stdlib.h>
#include "LinkPriorityQueue.h"
void InitLPQ(PLPQ *pLPQAddr)
{
*pLPQAddr = (PLPQ)malloc(sizeof(LinkPriorityQueue));
(*pLPQAddr)->pRear = NULL;
(*pLPQAddr)->pFront = NULL;
(*pLPQAddr)->nCount = 0;
}
BOOL IsLPQEmpty(PLPQ pLPQ)
{
if(pLPQ == NULL)
{
return TRUE;
}
if(pLPQ->nCount == 0)
{
return TRUE;
}
else
{
return FALSE;
}
}
int LPQAppend(PLPQ pLPQ, EleType et)
{
LPQNode *pNewLPQNode;
if(pLPQ == NULL)
{
return ERROR;
}
pNewLPQNode = (LPQNode*)malloc(sizeof(LPQNode));
pNewLPQNode->eleData.data =et.data;
pNewLPQNode->eleData.nPriority = et.nPriority;
pNewLPQNode->pNext = NULL;
if(pLPQ->pRear != NULL)
{
pLPQ->pRear->pNext = pNewLPQNode;
}
pLPQ->pRear = pNewLPQNode;
if(pLPQ->pFront == NULL)
{
pLPQ->pFront = pNewLPQNode;
}
++(pLPQ->nCount);
return SUCCESS;
}
int LPQDelete(PLPQ pLPQ, EleType *et)
{
LPQNode *pIterator;
int nMaxPriority;
LPQNode *pMaxPriority, *pPrious, *pMaxPrious;
if(pLPQ == NULL || IsLPQEmpty(pLPQ) || et == NULL)
{
return ERROR;
}
/*
** Find the Max Priority Node.
*/
/* Set the max-priority node pointer. */
pMaxPriority = pLPQ->pFront;
/* Set the front of max-priority node pointer and prious pointer. */
pPrious = pMaxPrious = pLPQ->pFront;
pIterator = pMaxPriority->pNext;
/* Init the Max priority number. */
nMaxPriority = pMaxPriority->eleData.nPriority;
while(pIterator != NULL)
{
if(nMaxPriority > pIterator->eleData.nPriority)
{
nMaxPriority = pIterator->eleData.nPriority;
/* Save the Max-Priority node pointer. */
pMaxPriority = pIterator;
/* Save the Prious pointer. */
pMaxPrious = pPrious;
}
pPrious = pIterator;
pIterator = pIterator->pNext;
}
(*et).data = pMaxPriority->eleData.data;
(*et).nPriority = pMaxPriority->eleData.nPriority;
/* Check the pMaxPriority has changed. */
if(pMaxPriority != pLPQ->pFront)
{
/* pFront needn't changed. */
pMaxPrious->pNext = pMaxPriority->pNext;
}
else
{
/* pFront changed. */
pLPQ->pFront = pLPQ->pFront->pNext;
}
free(pMaxPriority);
--(pLPQ->nCount);
return SUCCESS;
}
int GetLPQ(PLPQ pLPQ, EleType *et)
{
LPQNode *pIterator;
int nMaxPriority;
LPQNode *pMaxPriority, *pPrious, *pMaxPrious;
if(pLPQ == NULL || IsLPQEmpty(pLPQ) || et == NULL)
{
return ERROR;
}
/* Find the Max Priority Node. */
pMaxPriority = pLPQ->pFront;
pPrious = pMaxPrious = pLPQ->pFront;
pIterator = pMaxPriority->pNext;
nMaxPriority = pLPQ->pFront->eleData.nPriority;
while(pIterator != NULL)
{
if(nMaxPriority > pIterator->eleData.nPriority)
{
nMaxPriority = pIterator->eleData.nPriority;
pMaxPriority = pIterator;
pMaxPrious = pPrious;
}
pPrious = pIterator;
pIterator = pIterator->pNext;
}
(*et).data = pMaxPriority->eleData.data;
(*et).nPriority = pMaxPriority->eleData.nPriority;
return SUCCESS;
}
void FreeLPQ(PLPQ *pLPQ)
{
LPQNode *pIterator, *pTemp;
pIterator = (*pLPQ)->pFront;
while(pIterator != NULL)
{
pTemp = pIterator;
pIterator = pIterator->pNext;
free(pTemp);
}
*pLPQ = NULL;
}
测试程序:
#include <stdio.h>
#include "LinkPriorityQueue.h"
#define TEST_SIZE 10
int main(int argc, char *argv[])
{
EleType et;
LinkPriorityQueue *pLPQ;
int i = 0;
InitLPQ(&pLPQ);
printf("[Original]\nPriority Data\n");
printf("-------- ----\n");
for(i = 0; i < TEST_SIZE / 2; ++i)
{
et.data = i;
et.nPriority = i;
LPQAppend(pLPQ, et);
printf("%5d%10d\n", et.nPriority, et.data);
}
for(i = TEST_SIZE / 2; i < TEST_SIZE; ++i)
{
et.data = i;
et.nPriority = i % (TEST_SIZE / 2);
printf("%5d%10d\n", et.nPriority, et.data);
LPQAppend(pLPQ, et);
}
/* Get the Max Priority Data. */
GetLPQ(pLPQ, &et);
printf("The max-priority is %d, data=%d.\n", et.nPriority, et.data);
printf("Priority Data\n");
printf("-------- ----\n");
while(LPQDelete(pLPQ, &et) == SUCCESS)
{
printf("%5d%10d\n", et.nPriority, et.data);
}
FreeLPQ(&pLPQ);
return 0;
}
输出截图:
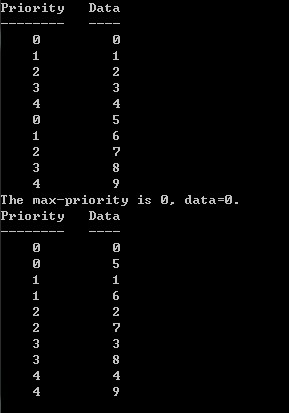
分享到:


相关推荐
10.链式队列以及优先级队列应用.ppt
总的来说,这个压缩包提供了关于数据结构——堆栈和队列的C语言实现,以及额外的数字转换和字符串处理功能。这些基础知识对于理解和编写高效的计算机程序至关重要。通过学习和理解这些内容,开发者能够更好地解决...
数据结构——栈和队列经典测试题 一、栈和队列的概念和特点 栈是一种特殊的线性表,允许插入和删除运算的一端称为栈顶,不允许插入和删除运算的一端称为栈底。栈的特点是后进先出(Last In First Out,LIFO),即...
链式存储是一种非顺序的内存数据结构,与传统的数组存储方式相比,它具有更大的灵活性。在数组中,元素是连续存储的,而链表则通过指针连接各个节点,使得元素可以在内存中的任意位置分布。这种数据结构在处理动态...
本篇笔记主要介绍了队列的概念以及两种常见的队列实现方式:顺序队列和链式队列,并提及了优先级队列的基本概念。 1. **队列的基本概念** 队列是一种特殊的线性表,它限制了元素的插入和删除操作。在队列的前端...
链式队列是一种在计算机科学中广泛使用的数据结构,它基于链表实现,与传统的数组队列相比,具有更大的灵活性。在本程序中,我们主要关注链式队列的六个核心操作,这些操作对于理解和应用链式队列至关重要。 1. **...
该文件实现链式队列功能,包含队列的创建queucreat、入队add与出队output,并通过打印显示函数的执行效果。
【链式结构实现线性表】是数据结构领域的一个基础实验,主要目的是让学生掌握线性表的操作以及指针、模板类、异常处理等C++编程技术。在这个实验中,学生可以选择五种不同的链式结构来实现线性表,分别是带头结点的...
给定的程序清单展示了链式队列(LinkedQueue)的实现,包括`makeEmpty`(清空队列)、`put_in`(入队)、`carry_out`(出队)等函数。在主函数`main`中,用户输入的命令被存入队列,然后逐个执行,模拟了命令的提交...
顺序队列和链式队列的实现 在计算机科学中,队列是一种重要的数据结构,广泛应用于多种领域。在本节中,我们将讨论顺序队列和链式队列的实现。 顺序队列 顺序队列是一种基于数组的队列实现方式。其主要特点是使用...
### 数据结构——车厢重排——队列问题 #### 核心知识点解析 ##### 1. 数据结构基础 在计算机科学中,数据结构是用于组织、管理以及存储数据的有效方式,以便能够高效地进行数据访问与修改操作。本案例中涉及的...
在Java中,队列的实现主要有三种:顺序队列、链式队列和循环队列。下面我们将详细探讨这三种队列的实现方式。 1. **顺序队列**: 顺序队列通常是基于数组实现的。在Java中,我们可以使用ArrayList或LinkedList来...
JAVA语言实现数据的链式结构 分享下挣挣人气
链式队列是一种基于链表的数据结构,常用于实现队列这种先进先出(FIFO,First In First Out)的数据组织方式。在C++中,链式队列可以通过定义一个节点类来存储队列中的元素,并通过头节点和尾节点来追踪队列的状态...
链式队列是一种在计算机科学中用于数据组织和操作的数据结构,它在概念上类似于现实生活中的排队等待。链式队列是数据结构课程中的一个重要概念,尤其对于学习C语言和其他编程语言的学生来说,理解并能实际操作链式...
链式队列是一种在计算机科学中广泛使用的数据结构,它属于线性数据结构的一种,用于实现队列这种抽象数据类型。在链式队列中,元素的存储位置不连续,而是通过指针链接起来,这使得插入和删除操作更加灵活。下面我们...
链式循环队列.cpp
将病人按照病情紧急程度分为两类,重病患者为高优先级队列(q2),普通病患为低优先级队列(q1)。在这样的设计下,系统将首先处理高优先级队列中的病人,之后处理低优先级队列中的病人。如果两个队列都存在病人,...
链式队列是一种数据结构,它是队列的一种特殊形式,主要使用链表来存储队列中的元素。在C语言中,链式队列的实现通常涉及结构体的定义、节点的创建与销毁、以及一系列针对队列操作的函数。下面我们将深入探讨链式...
数据结构在计算机科学中扮演着至关重要的角色,而链式队列作为一种常用的数据结构,它在处理大量数据的入队和出队操作时表现出高效性。本篇文章将深入探讨链式队列的实现,以及与之相关的编程概念和技术。 首先,...