椭圆和直线、圆一样,是图形学领域中的一种常见图元,椭圆的生成算法(光栅转换算法)也是图形学软件中最常见的生成算法之一。在平面解析几何中,椭圆的方程可以描述为(x – x0)2 / a2+ (y – y0)2 / b2 = 1,其中(x0, y0)是圆心坐标,a和b是椭圆的长短轴,特别的,当(x0, y0)就是坐标中心点时,椭圆方程可以简化为x2 / a2 + y2 / b2 = 1。在计算机图形学中,椭圆图形也存在在点阵输出设备上显示或输出的问题,因此也需要一套光栅扫描转换算法。为了简化,我们先考虑圆心在原点的椭圆的生成,对于中心不是原点的椭圆,可以通过坐标的平移变换获得相应位置的椭圆。
在进行扫描转换之前,需要了解一下椭圆的对称性,如图(1)所示:
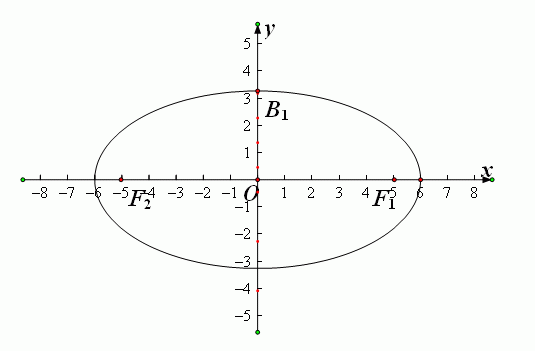
图(1)椭圆的对称性
中心在原点。焦点在坐标轴上的标准椭圆具有X轴对称、Y轴对称和原点对称特性,已知椭圆上第一象限的P点坐标是(x, y),则椭圆在另外三个象限的对称点分别是(x, -y)、(-x, y)和(-x, -y)。因此,只要画出第一象限的四分之一椭圆,就可以利用这三个对称性得到整个椭圆。
在光栅设备上输出椭圆有很多种方法,可以根据直角平面坐标方程直接求解点坐标,yekeyii利用极坐标方程求解,但是因为涉及到浮点数取整,效果都不好,一般都不使用直接求解的方式。本文就介绍几种计算机图形学中两种比较常用的椭圆生成方法:中点画椭圆算法和Bresenham椭圆生成算法。
1、 中点画椭圆法
中点在坐标原点,焦点在坐标轴上(轴对齐)的椭圆的平面集合方程是:
x2 / a2 + y2 / b2 = 1,也可以转化为如下非参数化方程形式:
F(x, y) = b2x2 + a2y2 - a2b2 = 0 (方程 1)
无论是中点画线算法、中点画圆算法还是本节要介绍的中点画椭圆算法,对选择x方向像素Δ增量还是y方向像素Δ增量都是很敏感的。举个例子,如果某段圆弧上,x方向上增量+1个像素时,y方向上的增量如果 < 1,则比较适合用中点算法,如果y方向上的增量 > 1,就会产生一些跳跃的点,最后生成的光栅位图圆弧会有一些突变的点,看起来好像不在圆弧上。因此,对于中点画圆弧算法,要区分出椭圆弧上哪段Δx增量变化显著,哪段Δy增量变化显著,然后区别对待。由于椭圆的对称性,我们只考虑第一象限的椭圆圆弧,如图(2)所示:
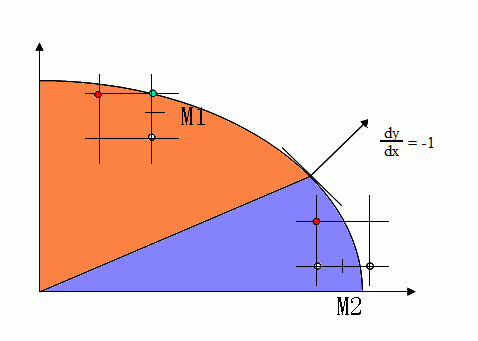
图(2)第一象限椭圆弧示意图
定义椭圆弧上某点的切线法向量N如下:

对方程1分别求x偏导和y偏导,最后得到椭圆弧上(x,y)点处的法向量是(2b2x, 2a2y)。dy/dx = -1的点是椭圆弧上的分界点。此点之上的部分(橙褐色部分)椭圆弧法向量的y分量比较大,即:2b2(x + 1) < 2a2(y – 0.5);此点之下的部分(蓝紫色部分)椭圆弧法向量的x分量比较大,即:2b2(x + 1) > 2a2(y – 0.5)。
对于图(2)中橙褐色标识的上部区域,y方向每变化1个单位,x方向变化大于一个单位,因此中点算法需要沿着x方向步进画点,x每次增量加1,求y的值。同理,对于图(2)中蓝紫色标识的下部区域,中点算法沿着y方向反向步进,y每次减1,求x的值。先来讨论上部区域椭圆弧的生成,如图(3)所示:

图(3)中点画椭圆算法对上部区域处理示意图
假设当前位置是P(xi, yi),则下一个可能的点就是P点右边的P1(xi+1, yi)点或右下方的P2(xi+1, yi-1)点,取舍的方法取决于判别式di,di的定义如下:
di = F(xi+1, yi-0.5) = b2(xi+1)2 + a2(yi-0.5)2 – a2b2
若di < 0,表示像素点P1和P2的中点在椭圆内,这时可取P1为下一个像素点。此时xi+1 = xi + 1,yi+1 = yi,代入判别式di得到di+1:
di+1 = F(xi+1+1, yi+1-0.5) = b2(xi+2)2 + a2(yi-0.5)2 – a2b2 = di + b2(2xi + 3)
计算出di的增量是b2(2xi + 3)。同理,若di >= 0,表示像素点P1和P2的中点在椭圆外,这时应当取P2为下一个像素点。此时xi+1 = xi + 1,yi+1 = yi - 1,代入判别式di得到di+1:
di+1 = F(xi+1+1, yi+1-0.5) = b2(xi+2)2 + a2(yi-1.5)2 – a2b2 = d1 + b2(2xi+3) + a2(-2yi+2)
计算出di的增量是b2(2xi+3)+a2(-2yi+2)。计算di的增量的目的是减少计算量,提高算法效率,每次判断一个点时,不必完整的计算判别式di,只需在上一次计算出的判别式上增加一个增量即可。
接下来继续讨论下部区域椭圆弧的生成,如图(4)所示:

图(4)中点画椭圆算法对下部区域处理示意图
假设当前位置是P(xi, yi),则下一个可能的点就是P点左下方的P1(xi -1, yi-1)点或下方的P2(xi, yi-1)点,取舍的方法同样取决于判别式di,di的定义如下:
di = F(xi+0.5, yi-1) = b2(xi+0.5)2 + a2(yi-1)2 – a2b2
若di < 0,表示像素点P1和P2的中点在椭圆内,这时可取P2为下一个像素点。此时xi+1 = xi + 1,yi+1 = yi - 1,代入判别式di得到di+1:
di+1 = F(xi+1+0.5, yi+1-1) = b2(xi+1.5)2 + a2(yi-2)2 – a2b2 = di + b2(2xi+2)+a2(-2yi+3)
计算出di的增量是b2(2xi+2)+a2(-2yi+3)。同理,若di >= 0,表示像素点P1和P2的中点在椭圆外,这时应当取P1为下一个像素点。此时xi+1 = xi,yi+1 = yi - 1,代入判别式di得到di+1:
di+1 = F(xi+1+0.5, yi+1-1) = b2(xi+0.5)2 + a2(yi-2)2 – a2b2 = d1 + a2(-2yi+3)
计算出di的增量是a2(-2yi+3)。
中点画椭圆算法从(0, b)点开始,第一个中点是(1, b – 0.5),判别式d的初始值是:
d0 = F(1, b–0.5) = b2 + a2(-b+0.25)
上部区域生成算法的循环终止条件是:2b2(x + 1) >= 2a2(y – 0.5),下部区域的循环终止条件是y = 0,至此,中点画椭圆算法就可以完整给出了:
20void MP_Ellipse(int xc , int yc , int a, int b)
21{
22 double sqa = a * a;
23 double sqb = b * b;
24
25 double d = sqb + sqa * (-b + 0.25);
26 int x = 0;
27 int y = b;
28 EllipsePlot(xc, yc, x, y);
29 while( sqb * (x + 1) < sqa * (y - 0.5))
30 {
31 if (d < 0)
32 {
33 d += sqb * (2 * x + 3);
34 }
35 else
36 {
37 d += (sqb * (2 * x + 3) + sqa * (-2 * y + 2));
38 y--;
39 }
40 x++;
41 EllipsePlot(xc, yc, x, y);
42 }
43 d = (b * (x + 0.5)) * 2 + (a * (y - 1)) * 2 - (a * b) * 2;
44 while(y > 0)
45 {
46 if (d < 0)
47 {
48 d += sqb * (2 * x + 2) + sqa * (-2 * y + 3);
49 x++;
50 }
51 else
52 {
53 d += sqa * (-2 * y + 3);
54 }
55 y--;
56 EllipsePlot(xc, yc, x, y);
57 }
58}
|
EllipsePlot()函数利用椭圆的三个对称性,一次完成四个对称点的绘制,因为简单,此处就不再列出代码。
2、 Bresenham算法
中点画椭圆法中,计算判别式d使用了浮点运算,影响了椭圆的生成效率。如果能将判别式规约到整数运算,则可以简化计算,提高效率。于是人们针对中点画椭圆法进行了多种改进,提出了很多种中点生成椭圆的整数型算法,Bresenham椭圆生成算法就是其中之一。
在生成椭圆上部区域时,以x轴为步进方向,如图(5-a)所示:
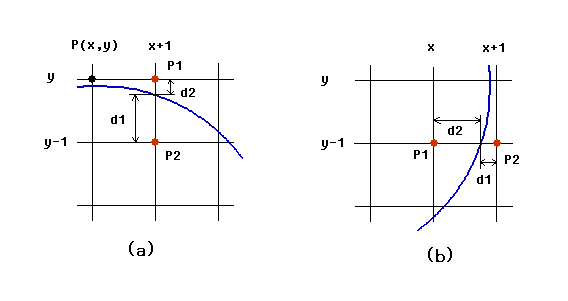
图(5)Bresenham椭圆生成算法判别式
x每步进一个单位,就需要在判断y保持不变还是也步进减1,bresenham算法定义判别式为:
D = d1 – d2
如果D < 0,则取P1为下一个点,否则,取P2为下一个点。采用判别式D,避免了中点算法因y-0.5而引入的浮点运算,使得判别式规约为全整数运算,算法效率得到了很大的提升。根据椭圆方程,可以计算出d1和d2分别是:
d1 = a2(yi2 – y2)
d2 = a2(y2 – yi+12)
以(0, b)作为椭圆上部区域的起点,将其代入判别式D可以得到如下递推关系:
Di+1 = Di + 2b2(2xi + 3) (Di < 0)
Di+1 = Di + 2b2(2xi + 3) – 4a2(yi - 1) (Di >= 0)
D0 = 2b2 – 2a2b + a2
在生成椭圆下部区域时,以y轴为步进方向,如图(5-b)所示,y每步进减一个单位,就需要在判断x保持不变还是步进加一个单位,对于下部区域,计算出d1和d2分别是:
d1 = b2(xi+12 – x2)
d2 = b2(x2 – xi2)
以(xp, yp)作为椭圆下部区域的起点,将其代入判别式D可以得到如下递推关系:
Di+1 = Di – 4a2(yi - 1) + 2a2 (Di < 0)
Di+1 = Di + 2b2(xi + 1) – 4a2(y - 1) + 2a2 + b2 (Di >= 0)
D0 = b2(xp + 1)2 +b2xp2 - 2a2b2 + 2a2(yp - 1)2
根据以上分析,Bresenham椭圆生成算法的实现就比较简单了:
61void Bresenham_Ellipse(int xc , int yc , int a, int b)
62{
63 int sqa = a * a;
64 int sqb = b * b;
65
66 int x = 0;
67 int y = b;
68 int d = 2 * sqb - 2 * b * sqa + sqa;
69 EllipsePlot(xc, yc, x, y);
70 int P_x = ROUND_INT( (double)sqa/sqrt((double)(sqa+sqb)) );
71 while(x <= P_x)
72 {
73 if(d < 0)
74 {
75 d += 2 * sqb * (2 * x + 3);
76 }
77 else
78 {
79 d += 2 * sqb * (2 * x + 3) - 4 * sqa * (y - 1);
80 y--;
81 }
82 x++;
83 EllipsePlot(xc, yc, x, y);
84 }
85
86 d = sqb * (x * x + x) + sqa * (y * y - y) - sqa * sqb;
87 while(y >= 0)
88 {
89 EllipsePlot(xc, yc, x, y);
90 y--;
91 if(d < 0)
92 {
93 x++;
94 d = d - 2 * sqa * y - sqa + 2 * sqb * x + 2 * sqb;
95 }
96 else
97 {
98 d = d - 2 * sqa * y - sqa;
99 }
100 }
101}
|
总结一下,本文介绍了两种计算机图形学中常见的椭圆生成算法,实际上还有很多种改进算法,包括提高效率,引入反走样技术等等,但那已经不是本文的重点,能把算法的基本原理讲清楚才是本文的目的。
参考资料:
【1】计算几何:算法设计与分析周培德 清华大学出版社 2005年
【2】计算几何:算法与应用德贝尔赫(邓俊辉译) 清华大学出版社 2005年
【3】计算机图形学孙家广、杨常贵清华大学出版社 1995年
分享到:















相关推荐
在计算机图形学中,直线、圆和椭圆的生成算法是基本且至关重要的部分,用于在屏幕上绘制这些几何形状。...在学习和实现这些算法时,可以参考“直线,圆,椭圆生成算法.ppt”中的详细内容,以加深理解和掌握。
Bresenham画圆算法是另一种常用的圆生成算法,该算法的基本原理是:设(xi, yi)为已确定的象素坐标,则下一个象素只能是以下三象素之一:H、D、V。五种情况:① H、D、V全在园内② H在园外,D、V在园内③ D在园上,H...
中点生成法画椭圆,给定圆心和半径,画出坐标轴
ECC算法的核心在于选择合适的椭圆曲线和基点。基点G是一个选定的非无穷远点,它满足群的乘法规则。私钥通常是一个随机选取的整数k,而公钥则是私钥k与基点G的点乘结果,即P = kG。加密时,明文消息经过某种编码转换...
直线圆椭圆生成算法PPT学习教案 本文主要介绍了直线圆椭圆生成算法,包括DDA算法、中点画线法和Bresenham画线算法等。下面是对每种算法的详细说明: 一、DDA算法 DDA(Digital Differential Analyzer)算法是一种...
因此在计算椭圆生成的时候,只需要计算1/4个椭圆,经过对称原理就可以实现其他3/4个椭圆的生成了,即:计算出目标点(x,y)的坐标,必然存在(x,-y)、(-x,y)(-x,-y)。此方案中采用计算第一象限中椭圆的生成,即...
这个算法是由F.Bresenham在1965年提出的一种改进版,它针对椭圆的特性进行了优化,适用于低级编程语言如C语言,能够有效地在屏幕上生成精确的椭圆图形。 在计算机中,椭圆通常可以通过数学方程来表示,如标准形式的...
在这个实验中,我们将深入理解并实践这个算法在圆和椭圆生成中的应用。 首先,我们要掌握圆的中点Bresenham生成算法。这个算法的基本思想是通过迭代计算每个像素点是否应该被着色,以逐步逼近圆形。在算法中,我们...
采用完全Bresenham算法生成椭圆,有别于中点Bresenham算法生成椭圆
图形学课件中,基本二维图元的生成算法是计算机图形学的核心内容之一。本节课件主要介绍了基本二维图元的生成算法,包括直线、圆、椭圆、区域填充、字符生成、反走样、裁剪等内容。 基本二维图元的生成算法是计算机...
在计算机图形学中,圆和椭圆的生成算法是至关重要的组成部分,特别是在2D图形绘制和游戏开发中。本文将详细解析"圆和椭圆的生成算法演示"中涉及的知识点,以及如何使用VC6.0这样的编程环境来实现它们。 首先,我们...
上述代码的作用是使用椭圆曲线加密算法(Elliptic Curve Cryptography, ECC)来生成一个密钥对,并进一步计算系统公钥。具体来说,它包括以下步骤: 定义哈希函数:代码定义了四个不同的哈希函数(H1、H2、H3、H4)...
3. 正向计算(由私钥计算公钥)确定椭圆曲线一个点作为基点 P,由于所有的点构成一个有限群,那么基点 P 必然可以作为一个生成元生成一个子群。 椭圆曲线密码算法的实现: 1. 椭圆曲线密码体制需要大数运算,需要...
综上所述,"椭圆曲线加密算法密钥生成器"是一个利用国家商用密码开放动态库的工具,用于生成ECC算法所需的密钥对,以实现高效且安全的加密和签名操作。OpenSM.dll提供了底层的密码学支持,而ECKeyPair.exe则是一个...
本主题聚焦于两种特定的算法:中点画圆算法和Bresenham画圆算法,以及它们在C++环境下利用`graphics.h`库实现的方式。`graphics.h`是一个图形库,通常用于Turbo C++编译器,它提供了简单的图形函数接口,便于初学者...
首先,直线算法是计算机图形学中最基本的元素之一。它包括多种方法,如Bresenham算法,DDA(Digital Differential Analyzer)算法等。Bresenham算法是一种快速、效率高的算法,用于在像素网格上近似绘制直线。它的...
应用带域提出了一种误差最小的椭圆生成算法,得到递推公式,每次要计算的是朝X方向或Y方向取像素点的个数,跟过去一贯采用的每生成一个像素点都要计算判别函数的传统方法比较,具有较强的优越性,尤其是对长轴与短轴...
- **运算层次**:椭圆曲线加密算法的实现可以分为三个层次:域运算层、椭圆曲线操作层和协议层。域运算层处理基本的数学运算,椭圆曲线操作层实现点乘等椭圆曲线特有运算,协议层则负责密钥交换和数字签名等功能。 ...
中点椭圆算法是一种在计算机图形学中广泛使用的算法,用于高效地绘制椭圆或圆形。这个算法基于数学原理,可以很容易地用编程语言实现,比如Python。在PyCharm集成开发环境中,结合 PyQt5 框架,我们可以创建一个具有...