本文转自:http://www.blogjava.net/zhenandaci/archive/2009/03/17/260315.html
接下来要说的东西其实不是松弛变量本身,但由于是为了使用松弛变量才引入的,因此放在这里也算合适,那就是惩罚因子C。回头看一眼引入了松弛变量以后的优化问题:
注意其中C的位置,也可以回想一下C所起的作用(表征你有多么重视离群点,C越大越重视,越不想丢掉它们)。这个式子是以前做SVM的人写的,大家也就这么用,但没有任何规定说必须对所有的松弛变量都使用同一个惩罚因子,我们完全可以给每一个离群点都使用不同的C,这时就意味着你对每个样本的重视程度都不一样,有些样本丢了也就丢了,错了也就错了,这些就给一个比较小的C;而有些样本很重要,决不能分类错误(比如中央下达的文件啥的,笑),就给一个很大的C。
当然实际使用的时候并没有这么极端,但一种很常用的变形可以用来解决分类问题中样本的“偏斜”问题。
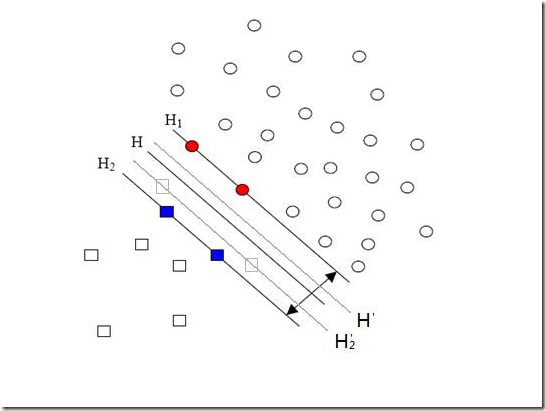
先来说说样本的偏斜问题,也叫数据集偏斜(unbalanced),它指的是参与分类的两个类别(也可以指多个类别)样本数量差异很大。比如说正类有10,000个样本,而负类只给了100个,这会引起的问题显而易见,可以看看下面的图:
方形的点是负类。H,H1,H2是根据给的样本算出来的分类面,由于负类的样本很少很少,所以有一些本来是负类的样本点没有提供,比如图中两个灰色的方形点,如果这两个点有提供的话,那算出来的分类面应该是H’,H2’和H1,他们显然和之前的结果有出入,实际上负类给的样本点越多,就越容易出现在灰色点附近的点,我们算出的结果也就越接近于真实的分类面。但现在由于偏斜的现象存在,使得数量多的正类可以把分类面向负类的方向“推”,因而影响了结果的准确性。
对付数据集偏斜问题的方法之一就是在惩罚因子上作文章,想必大家也猜到了,那就是给样本数量少的负类更大的惩罚因子,表示我们重视这部分样本(本来数量就少,再抛弃一些,那人家负类还活不活了),因此我们的目标函数中因松弛变量而损失的部分就变成了:
其中i=1…p都是正样本,j=p+1…p+q都是负样本。libSVM这个算法包在解决偏斜问题的时候用的就是这种方法。
那C+和C-怎么确定呢?它们的大小是试出来的(参数调优),但是他们的比例可以有些方法来确定。咱们先假定说C+是5这么大,那确定C-的一个很直观的方法就是使用两类样本数的比来算,对应到刚才举的例子,C-就可以定为500这么大(因为10,000:100=100:1嘛)。
但是这样并不够好,回看刚才的图,你会发现正类之所以可以“欺负”负类,其实并不是因为负类样本少,真实的原因是负类的样本分布的不够广(没扩充到负类本应该有的区域)。说一个具体点的例子,现在想给政治类和体育类的文章做分类,政治类文章很多,而体育类只提供了几篇关于篮球的文章,这时分类会明显偏向于政治类,如果要给体育类文章增加样本,但增加的样本仍然全都是关于篮球的(也就是说,没有足球,排球,赛车,游泳等等),那结果会怎样呢?虽然体育类文章在数量上可以达到与政治类一样多,但过于集中了,结果仍会偏向于政治类!所以给C+和C-确定比例更好的方法应该是衡量他们分布的程度。比如可以算算他们在空间中占据了多大的体积,例如给负类找一个超球——就是高维空间里的球啦——它可以包含所有负类的样本,再给正类找一个,比比两个球的半径,就可以大致确定分布的情况。显然半径大的分布就比较广,就给小一点的惩罚因子。
但是这样还不够好,因为有的类别样本确实很集中,这不是提供的样本数量多少的问题,这是类别本身的特征(就是某些话题涉及的面很窄,例如计算机类的文章就明显不如文化类的文章那么“天马行空”),这个时候即便超球的半径差异很大,也不应该赋予两个类别不同的惩罚因子。
看到这里读者一定疯了,因为说来说去,这岂不成了一个解决不了的问题?然而事实如此,完全的方法是没有的,根据需要,选择实现简单又合用的就好(例如libSVM就直接使用样本数量的比)。




![clip_image002[5] clip_image002[5]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_11A27/clip_image002%5B5%5D_thumb.gif)



相关推荐
### SVM入门:SVM的八股简介 #### 1.1 SVM的基本概念 支持向量机(Support Vector Machine,简称SVM)是一种监督学习模型,主要用于分类和回归分析。SVM最早是由Cortes和Vapnik在1995年提出的。其核心思想是在特征...
此时,可以通过引入松弛变量和惩罚因子来处理这种情况,允许某些样本点位于决策边界甚至错误分类,从而实现对复杂数据集的有效分类。 3. **核技巧**:为了处理非线性可分的问题,SVM采用了核技巧,即将原始数据...
为了处理这种情况,SVM引入了松弛变量,允许一定程度的误分类。 #### 五、核函数的作用 在处理非线性可分问题时,SVM通过使用核函数将低维空间中的非线性问题转换为高维空间中的线性问题。常见的核函数包括多项式...
- **软间隔**:在现实世界中,数据往往不是完全线性可分的,SVM引入了**松弛变量**和**惩罚项**,允许一定数量的样本可以穿过边界,但会受到相应惩罚。 - **核函数**:对于非线性可分的数据,SVM通过**核技巧**(如...
### SVM入门知识点详解 #### 一、SVM简介与背景 **支持向量机**(Support Vector Machine, SVM)是由Cortes和Vapnik在1995年首次提出的一种机器学习模型。作为一种监督学习方法,SVM在处理小样本、非线性和高维数据...
当数据不是线性可分时,SVM引入松弛变量来允许某些数据点轻微违反分类规则,以优化整体的分类边界。通过调整惩罚参数C,可以控制模型的复杂性和泛化能力之间的平衡。 #### 多类分类器的应用 SVM最初设计用于二分类...
### SVM入门:支持向量机详解 #### 一、SVM简介 支持向量机(Support Vector Machine,简称SVM)是由Cortes和Vapnik于1995年首次提出的机器学习算法。它是一种监督学习方法,在解决小样本、非线性和高维模式识别等...
- 通过允许一些数据点轻微违反分类规则,松弛变量能够使SVM模型更具鲁棒性,提高其泛化能力。 #### 三、多类分类 - SVM最初设计用于二分类问题,但在实际应用中,常常需要解决多类分类问题。 - **解决多类分类的...
### SVM入门:机器学习经典解析 #### 支持向量机(SVM):理论与实践的桥梁 **支持向量机(Support Vector Machine,简称SVM)**是由Cortes和Vapnik在1995年首次提出的,自那时起便在机器学习领域占据了举足轻重的...
- **软间隔**:对于非线性可分的情况,SVM允许一定程度的误分类,引入松弛变量来允许一些样本点落在决策边界内甚至错误分类,从而达到在保证泛化性能的同时减少过拟合的风险。 - **核技巧**:对于非线性可分问题,...
为此,SVM引入了松弛变量,允许一定数量的样本落在间隔内,以提高模型的泛化能力。 6. 多分类问题: SVM最初只处理二分类问题,但通过一对多、一对一或合页损失等方法可以扩展到多分类问题。 7. C参数与正则化: ...
### SVM入门(八):松弛变量详解 #### SVM与松弛变量背景 支持向量机(Support Vector Machine,简称SVM)是一种广泛应用于机器学习领域的监督学习算法,主要用于分类和回归任务。SVM的核心思想是在特征空间中...
为了处理非线性可分或噪声较大的情况,SVM引入了松弛变量和惩罚系数C,允许一部分样本落在间隔内,形成了所谓的软间隔。同时,通过核函数可以将原始数据非线性地映射到高维空间,使得在高维空间中实现线性可分,...
在实际应用中,SVM还引入了松弛变量(slack variables)来处理那些难以正确分类的数据点,允许一定数量的数据点越过决策边界,以增强模型的鲁棒性。松弛变量的引入使得SVM成为一种软间隔分类器,能够容忍一定程度的...
### SVM入门(九):松弛变量与惩罚因子C的应用及数据集偏斜问题处理 #### 一、惩罚因子C的概念及其重要性 在支持向量机(SVM)的学习过程中,松弛变量(slack variable)和惩罚因子C是两个非常重要的概念。在上一篇...
### SVM入门(五)线性分类器的求解——问题的描述Part2 #### 重要概念与背景 本文档旨在帮助读者理解支持向量机(SVM)中的线性分类器求解过程及其数学表述,特别关注于如何将线性分类器问题转化为优化问题,并讨论...
5. **软间隔与正则化**:解释为什么在实际应用中引入松弛变量和惩罚项,以及C参数的意义。 6. **多分类问题**:介绍一对一和一对多两种策略解决多分类问题的方法。 7. **SVM在实际问题中的应用**:可能包含SVM在...
- **软间隔**:在实际数据中,完全线性可分的情况很少见,SVM引入了松弛变量和惩罚项,允许一部分样本点“越界”,从而实现软间隔最大化。 - **核函数**:为了解决非线性问题,SVM使用核函数将原始特征空间映射到...