A new Graph Game
Time Limit: 8000/4000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1041 Accepted Submission(s): 468
Problem Description
An undirected graph is a graph in which the nodes are connected by undirected arcs. An undirected arc is an edge that has no arrow. Both ends of an undirected arc are equivalent--there is no head or tail. Therefore, we represent an edge in an undirected graph as a set rather than an ordered pair.
Now given an undirected graph, you could delete any number of edges as you wish. Then you will get one or more connected sub graph from the original one (Any of them should have more than one vertex).
You goal is to make all the connected sub graphs exist the Hamiltonian circuit after the delete operation. What’s more, you want to know the minimum sum of all the weight of the edges on the “Hamiltonian circuit” of all the connected sub graphs (Only one “Hamiltonian circuit” will be calculated in one connected sub graph! That is to say if there exist more than one “Hamiltonian circuit” in one connected sub graph, you could only choose the one in which the sum of weight of these edges is minimum).
For example, we may get two possible sums:
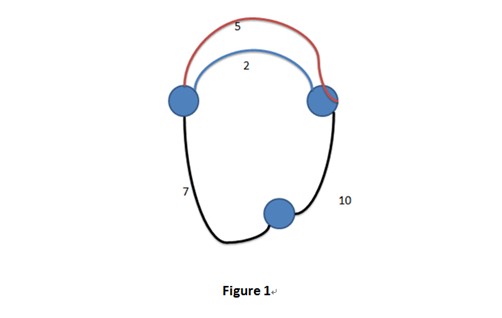
(1) 7 + 10 + 5 = 22
(2) 7 + 10 + 2 = 19
(There are two “Hamiltonian circuit” in this graph!)
Now given an undirected graph, you could delete any number of edges as you wish. Then you will get one or more connected sub graph from the original one (Any of them should have more than one vertex).
You goal is to make all the connected sub graphs exist the Hamiltonian circuit after the delete operation. What’s more, you want to know the minimum sum of all the weight of the edges on the “Hamiltonian circuit” of all the connected sub graphs (Only one “Hamiltonian circuit” will be calculated in one connected sub graph! That is to say if there exist more than one “Hamiltonian circuit” in one connected sub graph, you could only choose the one in which the sum of weight of these edges is minimum).
For example, we may get two possible sums:

(1) 7 + 10 + 5 = 22
(2) 7 + 10 + 2 = 19
(There are two “Hamiltonian circuit” in this graph!)
Input
In the first line there is an integer T, indicates the number of test cases. (T <= 20)
In each case, the first line contains two integers n and m, indicates the number of vertices and the number of edges. (1 <= n <=1000, 0 <= m <= 10000)
Then m lines, each line contains three integers a,b,c ,indicates that there is one edge between a and b, and the weight of it is c . (1 <= a,b <= n, a is not equal to b in any way, 1 <= c <= 10000)
In each case, the first line contains two integers n and m, indicates the number of vertices and the number of edges. (1 <= n <=1000, 0 <= m <= 10000)
Then m lines, each line contains three integers a,b,c ,indicates that there is one edge between a and b, and the weight of it is c . (1 <= a,b <= n, a is not equal to b in any way, 1 <= c <= 10000)
Output
Output “Case %d: “first where d is the case number counted from one. Then output “NO” if there is no way to get some connected sub graphs that any of them exists the Hamiltonian circuit after the delete operation. Otherwise, output the minimum sum of weight you may get if you delete the edges in the optimal strategy.
Sample Input
3
3 4
1 2 5
2 1 2
2 3 10
3 1 7
3 2
1 2 3
1 2 4
2 2
1 2 3
1 2 4
Sample Output
Case 1: 19
Case 2: NO
Case 3: 6
Hint
In Case 1:
You could delete edge between 1 and 2 whose weight is 5.
In Case 2:
It’s impossible to get some connected sub graphs that any of them exists the Hamiltonian circuit after the delete operation.
Author
AekdyCoin
Source
Recommend
zhouzeyong
我用的是KM算法,,依旧可用最大流,,//给顶点x和y间添加一条费用d,流量f的边 具体参见:http://blog.csdn.net/hqd_acm/article/details/6581979
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=1010;
const int INF=0x3f3f3f3f;
int n,m,nx,ny;
int linker[N],lx[N],ly[N],slack[N]; //lx,ly为顶标,nx,ny分别为x点集y点集的个数
int visx[N],visy[N],w[N][N];
int DFS(int x){
visx[x]=1;
for(int y=1;y<=ny;y++){
if(visy[y])
continue;
int tmp=lx[x]+ly[y]-w[x][y];
if(tmp==0){
visy[y]=1;
if(linker[y]==-1 || DFS(linker[y])){
linker[y]=x;
return 1;
}
}else if(slack[y]>tmp){ //不在相等子图中slack 取最小的
slack[y]=tmp;
}
}
return 0;
}
int KM(){
int i,j;
memset(linker,-1,sizeof(linker));
memset(ly,0,sizeof(ly));
for(i=1;i<=nx;i++) //lx初始化为与它关联边中最大的
for(j=1,lx[i]=-INF;j<=ny;j++)
if(w[i][j]>lx[i])
lx[i]=w[i][j];
for(int x=1;x<=nx;x++){
for(i=1;i<=ny;i++)
slack[i]=INF;
while(1){
memset(visx,0,sizeof(visx));
memset(visy,0,sizeof(visy));
if(DFS(x)) //若成功(找到了增广轨),则该点增广完成,进入下一个点的增广
break; //若失败(没有找到增广轨),则需要改变一些点的标号,使得图中可行边的数量增加。
//方法为:将所有在增广轨中(就是在增广过程中遍历到)的X方点的标号全部减去一个常数d,
//所有在增广轨中的Y方点的标号全部加上一个常数d
int d=INF;
for(i=1;i<=ny;i++)
if(!visy[i] && d>slack[i])
d=slack[i];
for(i=1;i<=nx;i++)
if(visx[i])
lx[i]-=d;
for(i=1;i<=ny;i++) //修改顶标后,要把所有不在交错树中的Y顶点的slack值都减去d
if(visy[i])
ly[i]+=d;
else
slack[i]-=d;
}
}
int res=0;
for(i=1;i<=ny;i++){
if(linker[i]==-1 || w[linker[i]][i]==-INF)
return -1;
res+=w[linker[i]][i];
}
return -res;
}
int main(){
//freopen("input.txt","r",stdin);
int t,cases=0;
scanf("%d",&t);
while(t--){
scanf("%d%d",&n,&m);
nx=ny=n;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
w[i][j]=-INF;
int u,v,cap;
while(m--){
scanf("%d%d%d",&u,&v,&cap);
if(w[u][v]<-cap)
w[u][v]=w[v][u]=-cap;
}
printf("Case %d: ",++cases);
int ans=KM();
if(ans!=-1)
printf("%d\n",ans);
else
printf("NO\n");
}
return 0;
}






相关推荐
Tour 最小费用圈覆盖**、**【HDU 3435】A new Graph Game**、**【HDU 3722】Card Game**、**【HDU 3718】Similarity 求相似度**:这些题目虽然不是直接与KMP算法相关,但标签中的“最小费用圈覆盖”可能涉及图论中的...
压缩包内的文件名“朝花夕拾——hdu”可能表示这是一系列关于HDU题目的代码记录,"朝花夕拾"是一个成语,意味着回忆过去的事情,这里可能是暗示这些代码是作者在过去解决HDU题目时留下的,现在整理出来分享或复习。...
14. **IO与NIO**:Java的I/O流系统以及新推出的非阻塞I/O(New IO,即NIO)。 15. **设计模式**:面向对象编程中的常见设计模式,如单例、工厂、观察者、装饰器等,可以提高代码的可读性和可维护性。 以上就是根据...
"hdu 2010"和"hdu 20"可能是该比赛的不同简称或分类,而"hdu acm20"可能指的是该赛事的第20届活动。这个压缩包可能是参赛者或教练分享的解题代码和资料。 【描述】提到的"水仙花数"问题,是计算机科学和算法竞赛中...
【标题】"hdu.rar_HDU 1089.cpp_OJ题求和_hdu_horsekw5_杭电obj" 提供的信息是关于一个压缩文件,其中包含了一个名为 "HDU 1089.cpp" 的源代码文件,这个文件是为了解决杭州电子科技大学(Hangzhou Dianzi ...
ACM HDU 题目分类 ACM HDU 题目分类是指对 HDU 在线判题系统中题目的分类,总结了大约十来个分类。这些分类将有助于编程选手更好地理解和解决问题。 DP 问题 DP(Dynamic Programming,动态规划)是一种非常重要...
### hdu1250高精度加法 #### 背景介绍 在计算机科学与编程竞赛中,处理大整数运算(特别是加法、减法、乘法等)是常见的需求之一。当数字的位数超过了标准数据类型(如`int`、`long`等)所能表示的最大值时,就需要...
根据提供的信息,我们可以总结出以下关于“hdu动态规划算法集锦”的知识点: ### 动态规划基础概念 动态规划是一种解决多阶段决策问题的方法,它通过将原问题分解为互相重叠的子问题,利用子问题的解来构建原问题...
根据给定的文件信息,我们可以得知这是一段用于解决HDU(Hdu Online Judge)编号为1241的问题的代码。该代码主要采用了深度优先搜索(DFS)算法来解决问题。 #### 二、DFS(Depth First Search)算法原理 **定义:...
【标题】"HDU DP动态规划"涉及到的是在算法领域中的动态规划(Dynamic Programming,简称DP)技术,这是解决复杂问题的一种高效方法,尤其适用于有重叠子问题和最优子结构的问题。动态规划通常用于优化多阶段决策...
数学在ACM竞赛中扮演着重要角色,包括数论(模运算、同余方程、欧几里得算法等)、组合数学(排列组合、容斥原理、鸽巢原理等)、图论(网络流、最大匹配等)。理解并运用这些数学知识,可以解决很多看似复杂的问题...
hdu1001解题报告
HDU1059的代码
hdu 1574 passed sorce
【标题】:杭电ACMhdu1163 【描述】:这是一道源自杭州电子科技大学(Hangzhou Dianzi University,简称HDU)的ACM编程竞赛题目,编号为1163。这类问题通常需要参赛者利用计算机编程解决数学、逻辑或算法上的挑战,...
【ACM HDU】指的是在ACM(国际大学生程序设计竞赛,International Collegiate Programming Contest)中,参赛者在杭州电子科技大学(Hangzhou Dianzi University,简称HDU)的在线评测系统上完成并已解决的题目集合...
hdu2101AC代码
hdu 5007 Post Robot 字符串枚举。 暴力一下就可以了。
8. **IDDFS(Iterative Deepening Depth-First Search)**:为了解决DFS可能导致栈溢出的问题,IDDFS结合了DFS和BFS的优点,每次加深搜索深度直到找到解或达到预设的最大深度,这样既避免了DFS的无限循环,又减少了...