šÄ░ňťĘŠłĹń╗ČňĚ▓š╗ĆŠŐŐńŞÇńެŠťČŠŁąš║┐ŠÇžńŞŹňĆ»ňłćšÜ䊾犝Čňłćš▒╗ÚŚ«Úóś´╝îÚÇÜŔ┐犜áň░äňł░Úźśš╗┤šę║ÚŚ┤ŔÇîňĆśŠłÉń║ćš║┐ŠÇžňĆ»ňłćšÜäŃÇéň░▒ňâĆńŞőňŤżŔ┐ÖŠáĚ´╝Ü
 
ňťćňŻóňĺ╣ňŻóšÜäšé╣ňÉ䊝늳ÉňŹâńŞŐńŞçńެ´╝łŠ»Ľšźč´╝îŔ┐Öň░▒Šś»ŠłĹń╗ČŔ«şš╗âÚŤćńŞşŠľçŠíúšÜ䊼░ÚçĆňśŤ´╝îňŻôšäÂňżłňĄžń║ć´╝ëŃÇéšÄ░ňťĘŠâ│Ŕ▒튳Ĺń╗ČŠťëňĆŽńŞÇńެŔ«şš╗âÚŤć´╝îňƬŠ»öňÄčňůłŔ┐ÖńެŔ«şš╗âÚŤćňĄÜń║ćńŞÇš»çŠľçšźá´╝áň░äňł░Úźśš╗┤šę║ÚŚ┤ń╗ąňÉÄ´╝łňŻôšä´╝îń╣čńŻ┐šöĘń║暍ŞňÉîšÜäŠáŞň篊Ľ░´╝ë´╝îń╣čň░▒ňĄÜń║ćńŞÇńެŠáĚŠťČšé╣´╝îńŻćŠś»Ŕ┐ÖńެŠáĚŠťČšÜäńŻŹšŻ«Šś»Ŕ┐ÖŠáĚšÜä´╝Ü
 
ň░▒Šś»ňŤżńŞşÚ╗äŔë▓Úéúńެšé╣´╝îň«âŠś»Šľ╣ňŻóšÜä´╝îňŤáŔÇîň«âŠś»Ŕ┤čš▒╗šÜäńŞÇńެŠáĚŠťČ´╝îŔ┐ÖňŹĽšőČšÜäńŞÇńެŠáĚŠťČ´╝îńŻ┐ňżŚňÄ芝Ț║┐ŠÇžňĆ»ňłćšÜäÚŚ«ÚóśňĆśŠłÉń║ćš║┐ŠÇžńŞŹňĆ»ňłćšÜäŃÇéŔ┐ÖŠáĚš▒╗ń╝╝šÜäÚŚ«Úóś´╝łń╗ůŠťëň░ĹŠĽ░šé╣š║┐ŠÇžńŞŹňĆ»ňłć´╝ëňĆźňüÜÔÇťŔ┐Ĺń╝╝š║┐ŠÇžňĆ»ňłćÔÇŁšÜäÚŚ«ÚóśŃÇé
ń╗ąŠłĹń╗Čń║║š▒╗šÜäňŞŞŔ»ćŠŁąňłĄŠľş´╝îŔ»┤ŠťëńŞÇńŞçńެšé╣Ú⯚ȎňÉłŠčÉšžŹŔžäňżő´╝łňŤáŔÇîš║┐ŠÇžňĆ»ňłć´╝ë´╝ëńŞÇńެšé╣ńŞŹšČŽňÉł´╝îÚéúŔ┐ÖńŞÇńެšé╣Šś»ňÉŽň░▒ń╗úŔíĘń║ćňłćš▒╗ŔžäňłÖńŞşŠłĹń╗ČŠ▓튝ëŔÇâŔÖĹňł░šÜ䊾╣ÚŁóňĹó´╝łňŤáŔÇîŔžäňłÖň║öŔ»ąńŞ║ň«âŔÇîňüÜňç║ń┐«Šö╣´╝ë´╝č
ňůÂň«×ŠłĹń╗Čń╝ÜŔžëňżŚ´╝┤ŠťëňĆ»Ŕ⯚Ü䊜»´╝îŔ┐ÖńެŠáĚŠťČšé╣ňÄőŠá╣ň░▒Šś»ÚöÖŔ»»´╝»ňÖ¬ňú░´╝»ŠĆÉńżŤŔ«şš╗âÚŤćšÜäňÉîňşŽń║║ňĚąňłćš▒╗ŠŚÂńŞÇŠëôš×íÚöÖŠöżŔ┐ŤňÄ╗šÜäŃÇéŠëÇń╗ąŠłĹń╗Čń╝Üš«ÇňŹĽšÜäň┐ŻšĽąŔ┐ÖńެŠáĚŠťČšé╣´╝îń╗ŹšäÂńŻ┐šöĘňÄ芣ąšÜäňłćš▒╗ňÖĘ´╝îňůŠĽłŠ×ťńŞŁŠ»źńŞŹňĆŚňŻ▒ňôŹŃÇé
ńŻćŔ┐ÖšžŹň»╣ňÖ¬ňú░šÜäň«╣ÚöÖŠÇžŠś»ń║║šÜäŠÇŁš╗┤ňŞŽŠŁąšÜä´╝Ĺń╗ČšÜäšĘőň║ĆňĆ»Š▓튝ëŃÇéšö▒ń║ÄŠłĹń╗ČňÄ芝ȚÜäń╝śňîľÚŚ«ÚóśšÜäŔíĘŔżżň╝ĆńŞş´╝îší«ň«×ŔŽüŔÇâŔÖĹŠëÇŠťëšÜäŠáĚŠťČšé╣´╝łńŞŹŔâŻň┐ŻšĽąŠčÉńŞÇńެ´╝îňŤáńŞ║šĘőň║Ćň«âŠÇÄń╣łščąÚüôŔ»ąň┐ŻšĽąňô¬ńŞÇńެňĹó´╝č´╝ë´╝îňťĘŠşĄňč║šíÇńŞŐň»╗ŠëżŠşúŔ┤čš▒╗ń╣őÚŚ┤šÜ䊝ÇňĄžňçáńŻĽÚŚ┤ÚÜö´╝îŔÇîňçáńŻĽÚŚ┤ÚÜöŠťČŔ║źń╗úŔíĘšÜ䊜»ŔĚŁšŽ╗´╝»ÚŁ×Ŕ┤čšÜä´╝îňâĆńŞŐÚŁóŔ┐ÖšžŹŠťëňÖ¬ňú░šÜäŠâůňćÁń╝ÜńŻ┐ňżŚŠĽ┤ńŞ¬ÚŚ«Ú󜊌áŔžúŃÇéŔ┐ÖšžŹŔžúŠ│ĽňůÂň«×ń╣čňĆźňüÜÔÇťšíČÚŚ┤ÚÜöÔÇŁňłćš▒╗Š│Ľ´╝îňŤáńŞ║ń╗ľšíČŠÇžšÜäŔŽüŠ▒éŠëÇŠťëŠáĚŠťČšé╣Ú⯊╗íŔÂ│ňĺîňłćš▒╗ň╣│ÚŁóÚŚ┤šÜäŔĚŁšŽ╗ň┐ůÚí╗ňĄžń║ÄŠčÉńެňÇ╝ŃÇé
ňŤáŠşĄšö▒ńŞŐÚŁóšÜäńżőňşÉńŞşń╣čňĆ»ń╗ąšťőňç║´╝îšíČÚŚ┤ÚÜöšÜäňłćš▒╗Š│Ľňůš╗ôŠ×ťň«╣ŠśôňĆŚň░ĹŠĽ░šé╣šÜäŠÄžňłÂ´╝îŔ┐ÖŠś»ňżłňŹ▒ÚÖęšÜä´╝łň░Żš«íŠťëňĆąŔ»ŁŔ»┤šťčšÉćŠÇ╗Šś»ŠÄîŠĆíňťĘň░ĹŠĽ░ń║║ŠëőńŞş´╝îńŻćÚéúńŞŹŔ┐犜»ÚéúńŞÇň░ĆŠĺ«ń║║ŔüŐń╗ąŔ笊ů░šÜäŔ»ŹňĆąšŻóń║ć´╝îňĺ▒Ŕ┐śŠś»ňżŚŠ░ĹńŞ╗´╝ëŃÇé
ńŻćŔžúňć│Šľ╣Š│Ľń╣čňżłŠśÄŠśż´╝îň░▒Šś»ń╗┐šůžń║║šÜäŠÇŁŔĚ»´╝îňůüŔ«ŞńŞÇń║Ťšé╣ňł░ňłćš▒╗ň╣│ÚŁóšÜäŔĚŁšŽ╗ńŞŹŠ╗íŔÂ│ňÄčňůłšÜäŔŽüŠ▒éŃÇéšö▒ń║ÄńŞŹňÉîšÜäŔ«şš╗âÚŤćňÉäšé╣šÜäÚŚ┤ŔĚŁň░║ň║ŽńŞŹňĄ¬ńŞÇŠáĚ´╝îňŤáŠşĄšöĘÚŚ┤ÚÜö´╝łŔÇîńŞŹŠś»ňçáńŻĽÚŚ┤ÚÜö´╝늣ąŔííÚçĆŠťëňłęń║ÄŠłĹń╗ČŔíĘŔżżňŻóň╝ĆšÜäš«ÇŠ┤üŃÇ銳Ĺń╗ČňÄčňůłň»╣ŠáĚŠťČšé╣šÜäŔŽüŠ▒銜»´╝Ü
 
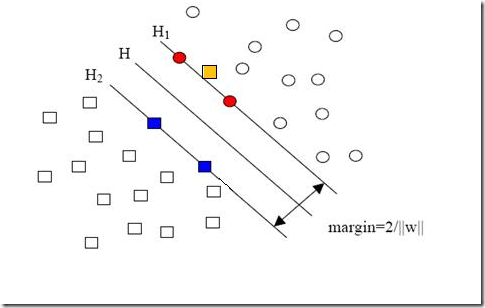
ŠäĆŠÇŁŠś»Ŕ»┤šŽ╗ňłćš▒╗ÚŁóŠťÇŔ┐ĹšÜäŠáĚŠťČšé╣ň篊Ľ░ÚŚ┤ÚÜöń╣čŔŽüŠ»ö1ňĄžŃÇéňŽéŠ×ťŔŽüň╝Ľňůąň«╣ÚöÖŠÇž´╝îň░▒š╗Ö1Ŕ┐ÖńެšíČŠÇžšÜäÚśłňÇ╝ňŐáńŞÇńެŠŁżň╝ŤňĆśÚçĆ´╝îňŹ│ňůüŔ«Ş
ňŤáńŞ║ŠŁżň╝ŤňĆśÚçĆŠś»ÚŁ×Ŕ┤čšÜä´╝îňŤáŠşĄŠťÇš╗łšÜäš╗ôŠ×ťŠś»ŔŽüŠ▒éÚŚ┤ÚÜöňĆ»ń╗ąŠ»ö1ň░ĆŃÇéńŻćŠś»ňŻôŠčÉń║Ťšé╣ňç║šÄ░Ŕ┐ÖšžŹÚŚ┤ÚÜöŠ»ö1ň░ĆšÜäŠâůňćÁŠŚÂ´╝łŔ┐Öń║Ťšé╣ń╣čňĆźšŽ╗šżĄšé╣´╝ë´╝îŠäĆňĹ│šŁÇŠłĹń╗ČŠöżň╝âń║ćň»╣Ŕ┐Öń║Ťšé╣šÜäš▓żší«ňłćš▒╗´╝îŔÇîŔ┐Öň»╣ŠłĹń╗ČšÜäňłćš▒╗ňÖĘŠŁąŔ»┤Šś»šžŹŠŹčňĄ▒ŃÇéńŻćŠś»Šöżň╝âŔ┐Öń║Ťšé╣ń╣čňŞŽŠŁąń║ćňąŻňĄä´╝îÚéúň░▒Šś»ńŻ┐ňłćš▒╗ÚŁóńŞŹň┐ůňÉĹŔ┐Öń║Ťšé╣šÜ䊾╣ňÉĹšž╗ňŐĘ´╝îňŤáŔÇîňĆ»ń╗ąňżŚňł░ŠŤ┤ňĄžšÜäňçáńŻĽÚŚ┤ÚÜö´╝łňťĘńŻÄš╗┤šę║ÚŚ┤šťőŠŁą´╝îňłćš▒╗Ŕż╣šĽîń╣芍┤ň╣│Š╗Ĺ´╝ëŃÇ銜żšäŠłĹń╗Čň┐ůÚí╗ŠŁâŔííŔ┐ÖšžŹŠŹčňĄ▒ňĺîňąŻňĄäŃÇéňąŻňĄäňżłŠśÄŠśż´╝Ĺń╗ČňżŚňł░šÜäňłćš▒╗ÚŚ┤ÚÜöŔÂŐňĄž´╝îňąŻňĄäň░▒ŔÂŐňĄÜŃÇéňŤ×ÚíżŠłĹń╗ČňÄčňžőšÜäšíČÚŚ┤ÚÜöňłćš▒╗ň»╣ň║öšÜäń╝śňîľÚŚ«Úóś´╝Ü
||w||2ň░▒Šś»ŠłĹń╗ČšÜ䚍«Šáçň篊Ľ░´╝łňŻôšäš│╗ŠĽ░ňĆ»ŠťëňĆ»ŠŚá´╝ë´╝îňŞîŠťŤň«âŔÂŐň░ĆŔÂŐňąŻ´╝îňŤáŔÇčňĄ▒ň░▒ň┐ůšäŠś»ńŞÇńެŔâŻńŻ┐ń╣őňĆśňĄžšÜäÚçĆ´╝łŔâŻńŻ┐ň«âňĆśň░Ćň░▒ńŞŹňĆźŠŹčňĄ▒ń║ć´╝Ĺń╗ČŠťČŠŁąň░▒ňŞîŠťŤšŤ«Šáçň篊Ľ░ňÇ╝ŔÂŐň░ĆŔÂŐňąŻ´╝ëŃÇéÚéúňŽéńŻĽŠŁąŔííÚçĆŠŹčňĄ▒´╝ëńŞĄšžŹňŞŞšöĘšÜ䊾╣ň╝Ć´╝ëń║║ňľťŠČóšöĘ
ŔÇëń║║ňľťŠČóšöĘ
ňůÂńŞşlÚ⯊ś»ŠáĚŠťČšÜ䊼░šŤ«ŃÇéńŞĄšžŹŠľ╣Š│ĽŠ▓튝ëňĄžšÜäňî║ňłźŃÇéňŽéŠ×ťÚÇëŠőęń║ćšČČńŞÇšžŹ´╝îňżŚňł░šÜ䊾╣Š│ĽšÜäň░▒ňĆźňüÜń║îÚśÂŔŻ»ÚŚ┤ÚÜöňłćš▒╗ňÖĘ´╝îšČČń║îšžŹň░▒ňĆźňüÜńŞÇÚśÂŔŻ»ÚŚ┤ÚÜöňłćš▒╗ňÖĘŃÇéŠŐŐŠŹčňĄ▒ňŐáňůąňł░šŤ«Šáçň篊Ľ░ÚçîšÜ䊌ÂňÇÖ´╝îň░▒ÚťÇŔŽüńŞÇńެŠâꚯÜňŤáňşÉ´╝łcost´╝îń╣čň░▒Šś»libSVMšÜäŔ»ŞňĄÜňĆ銼░ńŞşšÜäC´╝ë´╝îňÄ芣ąšÜäń╝śňîľÚŚ«Úóśň░▒ňĆśŠłÉń║ćńŞőÚŁóŔ┐ÖŠáĚ´╝Ü
Ŕ┐Öńެň╝ĆňşÉŠťëŔ┐Öń╣łňçášé╣ŔŽüŠ│ĘŠäĆ´╝Ü
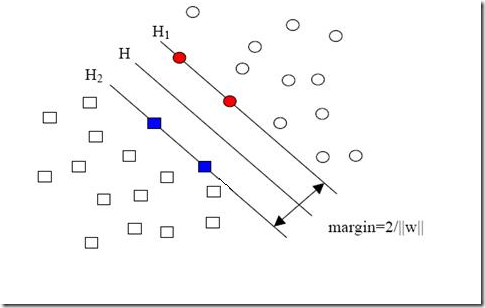
ńŞÇŠś»ň╣Âڣ׊ëÇŠťëšÜäŠáĚŠťČšé╣Ú⯊ťëńŞÇńެŠŁżň╝ŤňĆśÚçĆńŞÄňůÂň»╣ň║öŃÇéň«×ÚÖůńŞŐňƬŠťëÔÇťšŽ╗šżĄšé╣ÔÇŁŠëŹŠťë´╝ľŔÇůń╣čňĆ»ń╗ąŔ┐Öń╣łšťő´╝îŠëÇŠťëŠ▓횎╗šżĄšÜäšé╣ŠŁżň╝ŤňĆśÚçĆÚ⯚şëń║Ä0´╝łň»╣Ŕ┤čš▒╗ŠŁąŔ»┤´╝╗šżĄšé╣ň░▒Šś»ňťĘňëŹÚŁóňŤżńŞş´╝îŔĚĹňł░H2ňĆ│ńżžšÜäÚéúń║ŤŔ┤čŠáĚŠťČšé╣´╝îň»╣Šşúš▒╗ŠŁąŔ»┤´╝îň░▒Šś»ŔĚĹňł░H1ňĚŽńżžšÜäÚéúń║ŤŠşúŠáĚŠťČšé╣´╝ëŃÇé
ń║»ŠŁżň╝ŤňĆśÚçĆšÜäňÇ╝ň«×ÚÖůńŞŐŠá皥║ňç║ń║ćň»╣ň║öšÜäšé╣ňł░ň║ĽšŽ╗šżĄŠťëňĄÜŔ┐ť´╝îňÇ╝ŔÂŐňĄž´╝îšé╣ň░▒ŔÂŐŔ┐ťŃÇé
ńŞëŠś»ŠâꚯÜňŤáňşÉCňć│ň«Üń║ćńŻáŠťëňĄÜÚçŹŔžćšŽ╗šżĄšé╣ňŞŽŠŁąšÜ䊏čňĄ▒´╝żšäÂňŻôŠëÇŠťëšŽ╗šżĄšé╣šÜ䊣żň╝ŤňĆśÚçĆšÜäňĺîńŞÇň«ÜŠŚÂ´╝îńŻáň«ÜšÜäCŔÂŐňĄž´╝îň»╣šŤ«Šáçň篊Ľ░šÜ䊏čňĄ▒ń╣čŔÂŐňĄž´╝ĄŠŚÂň░▒ŠÜŚšĄ║šŁÇńŻáÚŁ×ňŞŞńŞŹŠä┐ŠäĆŠöżň╝âŔ┐Öń║ŤšŽ╗šżĄšé╣´╝NJ×üšź»šÜäŠâůňćÁŠś»ńŻáŠŐŐCň«ÜńŞ║ŠŚáÚÖÉňĄž´╝îŔ┐ÖŠáĚňƬŔŽüšĘŹŠťëńŞÇńެšé╣šŽ╗šżĄ´╝«Šáçň篊Ľ░šÜäňÇ╝ÚęČńŞŐňĆśŠłÉŠŚáÚÖÉňĄž´╝îÚęČńŞŐŔ«ęÚŚ«ÚóśňĆśŠłÉŠŚáŔžú´╝îŔ┐Öň░▒ÚÇÇňłÉń║ćšíČÚŚ┤ÚÜöÚŚ«ÚóśŃÇé
ňŤŤŠś»ŠâꚯÜňŤáňşÉCńŞŹŠś»ńŞÇńެňĆśÚçĆ´╝┤ńެń╝śňîľÚŚ«ÚóśňťĘŔžúšÜ䊌ÂňÇÖ´╝îCŠś»ńŞÇńެńŻáň┐ůÚí╗ń║őňůłŠîçň«ÜšÜäňÇ╝´╝îŠîçň«ÜŔ┐ÖńެňÇ╝ń╗ąňÉÄ´╝îŔžúńŞÇńŞő´╝îňżŚňł░ńŞÇńެňłćš▒╗ňÖĘ´╝îšäÂňÉÄšöĘŠÁőŔ»ĽŠĽ░ŠŹ«šťőšťőš╗ôŠ×ťŠÇÄń╣łŠáĚ´╝îňŽéŠ×ťńŞŹňĄčňąŻ´╝óńŞÇńެCšÜäňÇ╝´╝îňćŹŔžúńŞÇŠČíń╝śňîľÚŚ«Úóś´╝îňżŚňł░ňĆŽńŞÇńެňłćš▒╗ňÖĘ´╝îň揚ťőšťőŠĽłŠ×ť´╝îňŽéŠşĄň░▒Šś»ńŞÇńެňĆ銼░ň»╗ń╝śšÜäŔ┐çšĘő´╝îńŻćŔ┐Öňĺîń╝śňîľÚŚ«Ú󜊝ČŔ║źňć│ńŞŹŠś»ńŞÇňŤ×ń║ő´╝îń╝śňîľÚŚ«ÚóśňťĘŔžúšÜäŔ┐çšĘőńŞş´╝îCńŞÇšŤ┤Šś»ň«ÜňÇ╝´╝îŔŽüŔ«░ńŻĆŃÇé
ń║öŠś»ň░Żš«íňŐáń║抣żň╝ŤňĆśÚçĆŔ┐Öń╣łńŞÇŔ»┤´╝îńŻćŔ┐Öńެń╝śňîľÚŚ«Úóśń╗ŹšäŠś»ńŞÇńެń╝śňîľÚŚ«Úóś´╝łŠ▒Ś´╝îŔ┐ÖńŞŹň║čŔ»Łń╣ł´╝ë´╝îŔžúň«âšÜäŔ┐çšĘőŠ»öŔÁĚňÄčňžőšÜäšíČÚŚ┤ÚÜöÚŚ«Ú󜊣ąŔ»┤´╝îŠ▓튝ëń╗╗ńŻĽŠŤ┤ňŐášë╣Š«ŐšÜäňť░Šľ╣ŃÇé
ń╗ÄňĄžšÜ䊾╣ÚŁóŔ»┤ń╝śňîľÚŚ«ÚóśŔžúšÜäŔ┐çšĘő´╝îň░▒Šś»ňůłŔ»ĽšŁÇší«ň«ÜńŞÇńŞőw´╝îń╣čň░▒Šś»ší«ň«Üń║ćňëŹÚŁóňŤżńŞşšÜäńŞëŠŁíšŤ┤š║┐´╝îŔ┐ÖŠŚÂšťőšťőÚŚ┤ÚÜöŠťëňĄÜňĄž´╝îňĆłŠťëňĄÜň░Ĺšé╣šŽ╗šżĄ´╝îŠŐŐšŤ«Šáçň篊Ľ░šÜäňÇ╝š«ŚńŞÇš«Ś´╝îň揊ŹóńŞÇš╗äńŞëŠŁíšŤ┤š║┐´╝łńŻáňĆ»ń╗ąšťőňł░´╝îňłćš▒╗šÜ䚍┤š║┐ńŻŹšŻ«ňŽéŠ×ťšž╗ňŐĘń║ć´╝ëń║ŤňÄ芣ąšŽ╗šżĄšÜäšé╣ń╝ÜňĆśňżŚńŞŹň揚Ž╗šżĄ´╝îŔÇëšÜ䊝ȊŁąńŞŹšŽ╗šżĄšÜäšé╣ń╝ÜňĆśŠłÉšŽ╗šżĄšé╣´╝ë´╝îň揊ŐŐšŤ«Šáçň篊Ľ░šÜäňÇ╝š«ŚńŞÇš«Ś´╝îňŽéŠşĄňżÇňĄŹ´╝łŔ┐şń╗ú´╝ë´╝┤ňł░ŠťÇš╗łŠëżňł░šŤ«Šáçň篊Ľ░ŠťÇň░ĆŠŚÂšÜäwŃÇé
ňĽ░ňŚŽń║ćŔ┐Öń╣łňĄÜ´╝îŔ»╗ŔÇůńŞÇň«ÜňĆ»ń╗ąÚęČńŞŐŔç¬ňĚ▒ŠÇ╗š╗ôňç║ŠŁą´╝żň╝ŤňĆśÚçĆń╣čň░▒Šś»ńެŔžúňć│š║┐ŠÇžńŞŹňĆ»ňłćÚŚ«ÚóśšÜ䊾╣Š│ĽšŻóń║ć´╝îńŻćŠś»ňŤ×Šâ│ńŞÇńŞő´╝îŠáŞň篊Ľ░šÜäň╝ĽňůąńŞŹń╣芜»ńŞ║ń║ćŔžúňć│š║┐ŠÇžńŞŹňĆ»ňłćšÜäÚŚ«Úóśń╣ł´╝čńŞ║ń╗Çń╣łŔŽüńŞ║ń║ćńŞÇńŞ¬ÚŚ«ÚóśńŻ┐šöĘńŞĄšžŹŠľ╣Š│ĽňĹó´╝č
ňůÂň«×ńŞĄŔÇůŔ┐śŠťëňż«ňŽÖšÜäńŞŹňÉîŃÇéńŞÇŔłČšÜäŔ┐çšĘőň║öŔ»ąŠś»Ŕ┐ÖŠáĚ´╝îŔ┐śń╗ąŠľçŠťČňłćš▒╗ńŞ║ńżőŃÇéňťĘňÄčňžőšÜäńŻÄš╗┤šę║ÚŚ┤ńŞş´╝îŠáĚŠťČšŤŞňŻôšÜäńŞŹňĆ»ňłć´╝áŔ«║ńŻáŠÇÄń╣łŠëżňłćš▒╗ň╣│ÚŁó´╝îŠÇ╗ń╝ÜŠťëňĄžÚçĆšÜ䚎╗šżĄšé╣´╝ĄŠŚÂšöĘŠáŞň篊Ľ░ňÉĹÚźśš╗┤šę║ÚŚ┤Šśáň░äńŞÇńŞő´╝îŔÖŻšäš╗ôŠ×ťń╗ŹšäŠś»ńŞŹňĆ»ňłćšÜä´╝îńŻćŠ»öňÄčňžőšę║ÚŚ┤ÚçîšÜäŔŽüŠŤ┤ňŐáŠÄąŔ┐Ĺš║┐ŠÇžňĆ»ňłćšÜäšŐŠÇü´╝łň░▒Šś»Ŕżżňł░ń║ćŔ┐Ĺń╝╝š║┐ŠÇžňĆ»ňłćšÜäšŐŠÇü´╝ë´╝ĄŠŚÂň揚öĘŠŁżň╝ŤňĆśÚçĆňĄäšÉćÚéúń║Ťň░ĹŠĽ░ÔÇťňćąÚíŻńŞŹňîľÔÇŁšÜ䚎╗šżĄšé╣´╝îň░▒š«ÇňŹĽŠťëŠĽłňżŚňĄÜňĽŽŃÇé
ŠťČŔŐéńŞşšÜä´╝łň╝Ć1´╝ëń╣čší«ň«×Šś»Šö»ŠîüňÉĹÚçĆŠť║ŠťÇŠťÇňŞŞšöĘšÜäňŻóň╝ĆŃÇéŔç│ŠşĄńŞÇńެŠ»öŔżâň«îŠĽ┤šÜäŠö»ŠîüňÉĹÚçĆŠť║ŠíćŠ×Âň░▒Šťëń║ć´╝îš«ÇňŹĽŔ»┤ŠŁą´╝îŠö»ŠîüňÉĹÚçĆŠť║ň░▒Šś»ńŻ┐šöĘń║ćŠáŞň篊Ľ░šÜäŔŻ»ÚŚ┤ÚÜöš║┐ŠÇžňłćš▒╗Š│ĽŃÇé
ńŞőńŞÇŔŐéń╝ÜŔ»┤Ŕ»┤ŠŁżň╝ŤňĆśÚçĆňëęńŞőšÜäńŞÇšé╣šé╣ńŞťŔą┐´╝îÚí║ńż┐ŠÉ×ńެŔ»╗ŔÇůŔ░âŠčą´╝îšťőšťőňĄžň«ÂŔ┐śŠâ│ńżâńżâSVMšÜäňô¬ń║ŤŠľ╣ÚŁóŃÇé



![clip_image002[5] clip_image002[5]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_D32/clip_image002%5B5%5D_thumb.gif)
![clip_image002[7] clip_image002[7]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_D32/clip_image002%5B7%5D_thumb.gif)
![clip_image002[9] clip_image002[9]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_D32/clip_image002%5B9%5D_thumb.gif)
![clip_image002[11] clip_image002[11]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_D32/clip_image002%5B11%5D_thumb.gif)
![clip_image002[13] clip_image002[13]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/SVM_D32/clip_image002%5B13%5D_thumb.gif)



šŤŞňů│ŠÄĘŔŹÉ
### SVMňůąÚŚĘ´╝ÜSVMšÜäňůźŔéíš«Çń╗ő #### 1.1 SVMšÜäňč║ŠťČŠŽéň┐Á Šö»ŠîüňÉĹÚçĆŠť║´╝łSupport Vector Machine´╝îš«Çšž░SVM´╝늜»ńŞÇšžŹšŤĹšŁúňşŽń╣áŠĘíň×ő´╝îńŞ╗ŔŽüšöĘń║Äňłćš▒╗ňĺîňŤ×ňŻĺňłćŠ×ÉŃÇéSVMŠťÇŠŚęŠś»šö▒CortesňĺîVapnikňťĘ1995ň╣┤ŠĆÉňç║šÜäŃÇéňůŠáŞň┐âŠÇŁŠâ│Šś»ňťĘšë╣ňżü...
ŠşĄŠŚÂ´╝îňĆ»ń╗ąÚÇÜŔ┐çň╝ĽňůąŠŁżň╝ŤňĆśÚçĆňĺîŠâꚯÜňŤáňşÉŠŁąňĄäšÉćŔ┐ÖšžŹŠâůňćÁ´╝îňůüŔ«ŞŠčÉń║ŤŠáĚŠťČšé╣ńŻŹń║Äňć│šşľŔż╣šĽîšöÜŔç│ÚöÖŔ»»ňłćš▒╗´╝îń╗ÄŔÇîň«×šÄ░ň»╣ňĄŹŠŁéŠĽ░ŠŹ«ÚŤćšÜ䊝늼łňłćš▒╗ŃÇé 3. **ŠáŞŠŐÇňĚž**´╝ÜńŞ║ń║ćňĄäšÉćڣך║┐ŠÇžňĆ»ňłćšÜäÚŚ«Úóś´╝îSVMÚççšöĘń║ćŠáŞŠŐÇňĚž´╝îňŹ│ň░ćňÄčňžőŠĽ░ŠŹ«...
- **ŔŻ»ÚŚ┤ÚÜö**´╝ÜňťĘšÄ░ň«×ńŞľšĽîńŞş´╝░ŠŹ«ňżÇňżÇńŞŹŠś»ň«îňůĘš║┐ŠÇžňĆ»ňłćšÜä´╝îSVMň╝Ľňůąń║ć**ŠŁżň╝ŤňĆśÚçĆ**ňĺî**ŠâꚯÜÚí╣**´╝îňůüŔ«ŞńŞÇň«ÜŠĽ░ÚçĆšÜäŠáĚŠťČňĆ»ń╗ąšę┐Ŕ┐çŔż╣šĽî´╝îńŻćń╝ÜňĆŚňł░šŤŞň║öŠâꚯÜŃÇé - **ŠáŞň篊Ľ░**´╝Üň»╣ń║Äڣך║┐ŠÇžňĆ»ňłćšÜ䊼░ŠŹ«´╝îSVMÚÇÜŔ┐ç**ŠáŞŠŐÇňĚž**´╝łňŽé...
ńŞ║ń║ćňĄäšÉćŔ┐ÖšžŹŠâůňćÁ´╝îSVMň╝Ľňůąń║抣żň╝ŤňĆśÚçĆ´╝îňůüŔ«ŞńŞÇň«ÜšĘőň║ŽšÜäŔ»»ňłćš▒╗ŃÇé #### ń║öŃÇüŠáŞň篊Ľ░šÜäńŻťšöĘ ňťĘňĄäšÉćڣך║┐ŠÇžňĆ»ňłćÚŚ«Ú󜊌´╝îSVMÚÇÜŔ┐çńŻ┐šöĘŠáŞň篊Ľ░ň░ćńŻÄš╗┤šę║ÚŚ┤ńŞşšÜäڣך║┐ŠÇžÚŚ«ÚóśŔŻČŠŹóńŞ║Úźśš╗┤šę║ÚŚ┤ńŞşšÜäš║┐ŠÇžÚŚ«ÚóśŃÇéňŞŞŔžüšÜäŠáŞň篊Ľ░ňîůŠőČňĄÜÚí╣ň╝Ć...
### SVMňůąÚŚĘščąŔ»ćšé╣Ŕ»ŽŔžú #### ńŞÇŃÇüSVMš«Çń╗őńŞÄŔâîŠÖ» **Šö»ŠîüňÉĹÚçĆŠť║**(Support Vector Machine, SVM)Šś»šö▒CortesňĺîVapnikňťĘ1995ň╣┤ÚŽľŠČíŠĆÉňç║šÜäńŞÇšžŹŠť║ňÖĘňşŽń╣áŠĘíň×őŃÇéńŻťńŞ║ńŞÇšžŹšŤĹšŁúňşŽń╣ኾ╣Š│Ľ´╝îSVMňťĘňĄäšÉćň░ĆŠáĚŠťČŃÇüڣך║┐ŠÇžňĺîÚźśš╗┤ŠĽ░ŠŹ«...
ňŻôŠĽ░ŠŹ«ńŞŹŠś»š║┐ŠÇžňĆ»ňłćŠŚÂ´╝îSVMň╝ĽňůąŠŁżň╝ŤňĆśÚçĆŠŁąňůüŔ«ŞŠčÉń║ŤŠĽ░ŠŹ«šé╣ŔŻ╗ňż«Ŕ┐ŁňĆŹňłćš▒╗ŔžäňłÖ´╝îń╗ąń╝śňĽ┤ńŻôšÜäňłćš▒╗Ŕż╣šĽîŃÇéÚÇÜŔ┐çŔ░⊼┤ŠâꚯÜňĆ銼░C´╝îňĆ»ń╗ąŠÄžňłÂŠĘíň×őšÜäňĄŹŠŁéŠÇžňĺîŠ│ŤňîľŔâŻňŐŤń╣őÚŚ┤šÜäň╣│ŔííŃÇé #### ňĄÜš▒╗ňłćš▒╗ňÖĘšÜäň║öšöĘ SVMŠťÇňłŁŔ«żŔ«íšöĘń║Äń║îňłćš▒╗...
### SVMňůąÚŚĘ´╝ÜŠö»ŠîüňÉĹÚçĆŠť║Ŕ»ŽŔžú #### ńŞÇŃÇüSVMš«Çń╗ő Šö»ŠîüňÉĹÚçĆŠť║´╝łSupport Vector Machine´╝îš«Çšž░SVM´╝늜»šö▒CortesňĺîVapnikń║Ä1995ň╣┤ÚŽľŠČíŠĆÉňç║šÜ䊝║ňÖĘňşŽń╣áš«ŚŠ│ĽŃÇéň«âŠś»ńŞÇšžŹšŤĹšŁúňşŽń╣ኾ╣Š│Ľ´╝îňťĘŔžúňć│ň░ĆŠáĚŠťČŃÇüڣך║┐ŠÇžňĺîÚźśš╗┤ŠĘíň╝ĆŔ»ćňłźšşë...
- ÚÇÜŔ┐çňůüŔ«ŞńŞÇń║ŤŠĽ░ŠŹ«šé╣ŔŻ╗ňż«Ŕ┐ŁňĆŹňłćš▒╗ŔžäňłÖ´╝żň╝ŤňĆśÚçĆŔâŻňĄčńŻ┐SVMŠĘíň×őŠŤ┤ňůĚÚ▓üŠúĺŠÇž´╝îŠĆÉÚźśňůŠ│ŤňîľŔâŻňŐŤŃÇé #### ńŞëŃÇüňĄÜš▒╗ňłćš▒╗ - SVMŠťÇňłŁŔ«żŔ«íšöĘń║Äń║îňłćš▒╗ÚŚ«Úóś´╝îńŻćňťĘň«×ÚÖůň║öšöĘńŞş´╝îňŞŞňŞŞÚťÇŔŽüŔžúňć│ňĄÜš▒╗ňłćš▒╗ÚŚ«ÚóśŃÇé - **Ŕžúňć│ňĄÜš▒╗ňłćš▒╗šÜä...
### SVMňůąÚŚĘ´╝łňůź´╝ë´╝ÜŠŁżň╝ŤňĆśÚçĆŔ»ŽŔžú #### SVMńŞÄŠŁżň╝ŤňĆśÚçĆŔâîŠÖ» Šö»ŠîüňÉĹÚçĆŠť║´╝łSupport Vector Machine´╝îš«Çšž░SVM´╝늜»ńŞÇšžŹň╣┐Š│Ťň║öšöĘń║ÄŠť║ňÖĘňşŽń╣áÚóćňččšÜ䚍ŚŁúňşŽń╣áš«ŚŠ│Ľ´╝îńŞ╗ŔŽüšöĘń║Äňłćš▒╗ňĺîňŤ×ňŻĺń╗╗ňŐíŃÇéSVMšÜäŠáŞň┐âŠÇŁŠâ│Šś»ňťĘšë╣ňżüšę║ÚŚ┤ńŞş...
### SVMňůąÚŚĘ´╝ÜŠť║ňÖĘňşŽń╣áš╗ĆňůŞŔžúŠ×É #### Šö»ŠîüňÉĹÚçĆŠť║´╝łSVM´╝ë´╝ÜšÉćŔ«║ńŞÄň«×ŔĚÁšÜäŠíąŠóü **Šö»ŠîüňÉĹÚçĆŠť║´╝łSupport Vector Machine´╝îš«Çšž░SVM´╝ë**Šś»šö▒CortesňĺîVapnikňťĘ1995ň╣┤ÚŽľŠČíŠĆÉňç║šÜä´╝îŔç¬ÚéúŠŚÂŔÁĚńż┐ňťĘŠť║ňÖĘňşŽń╣áÚóćňččňŹáŠŹ«ń║ćńŞżŔÂ│ŔŻ╗Ú珚Üä...
- **ŔŻ»ÚŚ┤ÚÜö**´╝Üň»╣ń║Äڣך║┐ŠÇžňĆ»ňłćšÜäŠâůňćÁ´╝îSVMňůüŔ«ŞńŞÇň«ÜšĘőň║ŽšÜäŔ»»ňłćš▒╗´╝îň╝ĽňůąŠŁżň╝ŤňĆśÚçĆŠŁąňůüŔ«ŞńŞÇń║ŤŠáĚŠťČšé╣ŔÉŻňťĘňć│šşľŔż╣šĽîňćůšöÜŔç│ÚöÖŔ»»ňłćš▒╗´╝îń╗ÄŔÇîŔżżňł░ňťĘń┐ŁŔ»üŠ│ŤňǞŔ⯚ÜäňÉÂňçĆň░ĹŔ┐çŠőčňÉłšÜäÚúÄÚÖęŃÇé - **ŠáŞŠŐÇňĚž**´╝Üň»╣ń║Äڣך║┐ŠÇžňĆ»ňłćÚŚ«Úóś´╝î...
ńŞ║ŠşĄ´╝îSVMň╝Ľňůąń║抣żň╝ŤňĆśÚçĆ´╝îňůüŔ«ŞńŞÇň«ÜŠĽ░ÚçĆšÜäŠáĚŠťČŔÉŻňťĘÚŚ┤ÚÜöňćů´╝îń╗ąŠĆÉÚźśŠĘíň×őšÜäŠ│ŤňîľŔâŻňŐŤŃÇé 6. ňĄÜňłćš▒╗ÚŚ«Úóś´╝Ü SVMŠťÇňłŁňƬňĄäšÉćń║îňłćš▒╗ÚŚ«Úóś´╝îńŻćÚÇÜŔ┐çńŞÇň»╣ňĄÜŃÇüńŞÇň»╣ńŞÇŠłľňÉłÚíÁŠŹčňĄ▒šşëŠľ╣Š│ĽňĆ»ń╗ąŠëęň▒Ľňł░ňĄÜňłćš▒╗ÚŚ«ÚóśŃÇé 7. CňĆ銼░ńŞÄŠşúňłÖňîľ´╝Ü ...
ńŞ║ń║ćňĄäšÉćڣך║┐ŠÇžňĆ»ňłćŠłľňÖ¬ňú░ŔżâňĄžšÜäŠâůňćÁ´╝îSVMň╝Ľňůąń║抣żň╝ŤňĆśÚçĆňĺîŠâꚯܚ│╗ŠĽ░C´╝îňůüŔ«ŞńŞÇÚâĘňłćŠáĚŠťČŔÉŻňťĘÚŚ┤ÚÜöňćů´╝îňŻóŠłÉń║ćŠëÇŔ░ôšÜäŔŻ»ÚŚ┤ÚÜöŃÇéňÉ´╝îÚÇÜŔ┐çŠáŞň篊Ľ░ňĆ»ń╗ąň░ćňÄčňžőŠĽ░ŠŹ«ÚŁ×š║┐ŠÇžňť░Šśáň░äňł░Úźśš╗┤šę║ÚŚ┤´╝îńŻ┐ňżŚňťĘÚźśš╗┤šę║ÚŚ┤ńŞşň«×šÄ░š║┐ŠÇžňĆ»ňłć´╝î...
ňťĘň«×ÚÖůň║öšöĘńŞş´╝îSVMŔ┐śň╝Ľňůąń║抣żň╝ŤňĆśÚçĆ´╝łslack variables´╝늣ąňĄäšÉćÚéúń║ŤÚÜżń╗ąŠşúší«ňłćš▒╗šÜ䊼░ŠŹ«šé╣´╝îňůüŔ«ŞńŞÇň«ÜŠĽ░ÚçĆšÜ䊼░ŠŹ«šé╣ŔÂŐŔ┐çňć│šşľŔż╣šĽî´╝îń╗ąňó×ň╝║ŠĘíň×őšÜäÚ▓üŠúĺŠÇžŃÇ銣żň╝ŤňĆśÚçĆšÜäň╝ĽňůąńŻ┐ňżŚSVMŠłÉńŞ║ńŞÇšžŹŔŻ»ÚŚ┤ÚÜöňłćš▒╗ňÖĘ´╝îŔâŻňĄčň«╣ň┐ŹńŞÇň«ÜšĘőň║ŽšÜä...
### SVMňůąÚŚĘ´╝łń║ö´╝ëš║┐ŠÇžňłćš▒╗ňÖĘšÜäŠ▒éŔžúÔÇöÔÇöÚŚ«ÚóśšÜäŠĆĆŔ┐░Part2 #### ÚçŹŔŽüŠŽéň┐ÁńŞÄŔâîŠÖ» ŠťČŠľçŠíúŠŚĘňťĘňŞ«ňŐęŔ»╗ŔÇůšÉćŔžúŠö»ŠîüňÉĹÚçĆŠť║(SVM)ńŞşšÜäš║┐ŠÇžňłćš▒╗ňÖĘŠ▒éŔžúŔ┐çšĘőňĆŐňůŠĽ░ňşŽŔíĘŔ┐░´╝îšë╣ňłźňů│Š│Ęń║ÄňŽéńŻĽň░ćš║┐ŠÇžňłćš▒╗ňÖĘÚŚ«ÚóśŔŻČňîľńŞ║ń╝śňîľÚŚ«Úóś´╝îň╣ÂŔ«ĘŔ«║...
### SVMňůąÚŚĘ´╝łń╣Ł´╝ë´╝ÜŠŁżň╝ŤňĆśÚçĆńŞÄŠâꚯÜňŤáňşÉCšÜäň║öšöĘňĆŐŠĽ░ŠŹ«ÚŤćňüĆŠľťÚŚ«ÚóśňĄäšÉć #### ńŞÇŃÇüŠâꚯÜňŤáňşÉCšÜ䊎éň┐ÁňĆŐňůÂÚçŹŔŽüŠÇž ňťĘŠö»ŠîüňÉĹÚçĆŠť║(SVM)šÜäňşŽń╣áŔ┐çšĘőńŞş´╝żň╝ŤňĆśÚçĆ(slack variable)ňĺîŠâꚯÜňŤáňşÉCŠś»ńŞĄńŞ¬ÚŁ×ňŞŞÚçŹŔŽüšÜ䊎éň┐ÁŃÇéňťĘńŞŐńŞÇš»ç...
5. **ŔŻ»ÚŚ┤ÚÜöńŞÄŠşúňłÖňîľ**´╝ÜŔžúÚçŐńŞ║ń╗Çń╣łňťĘň«×ÚÖůň║öšöĘńŞşň╝ĽňůąŠŁżň╝ŤňĆśÚçĆňĺîŠâꚯÜÚí╣´╝îń╗ąňĆŐCňĆ銼░šÜäŠäĆń╣ëŃÇé 6. **ňĄÜňłćš▒╗ÚŚ«Úóś**´╝Üń╗őš╗ŹńŞÇň»╣ńŞÇňĺîńŞÇň»╣ňĄÜńŞĄšžŹšşľšĽąŔžúňć│ňĄÜňłćš▒╗ÚŚ«ÚóśšÜ䊾╣Š│ĽŃÇé 7. **SVMňťĘň«×ÚÖůÚŚ«ÚóśńŞşšÜäň║öšöĘ**´╝ÜňĆ»ŔâŻňîůňÉźSVMňťĘ...
- **ŔŻ»ÚŚ┤ÚÜö**´╝ÜňťĘň«×ÚÖůŠĽ░ŠŹ«ńŞş´╝îň«îňůĘš║┐ŠÇžňĆ»ňłćšÜäŠâůňćÁňżłň░ĹŔžü´╝îSVMň╝Ľňůąń║抣żň╝ŤňĆśÚçĆňĺîŠâꚯÜÚí╣´╝îňůüŔ«ŞńŞÇÚâĘňłćŠáĚŠťČšé╣ÔÇťŔÂŐšĽîÔÇŁ´╝îń╗ÄŔÇîň«×šÄ░ŔŻ»ÚŚ┤ÚÜöŠťÇňĄžňîľŃÇé - **ŠáŞň篊Ľ░**´╝ÜńŞ║ń║ćŔžúňć│ڣך║┐ŠÇžÚŚ«Úóś´╝îSVMńŻ┐šöĘŠáŞň篊Ľ░ň░ćňÄčňžőšë╣ňżüšę║ÚŚ┤Šśáň░äňł░...