最长公共子序列(LCS)问题有两种方式定义子序列,一种是子序列不要求不连续,一种是子序列必须连续。上一章介绍了用两种算法解决子序列不要求连续的最终公共子序列问题,本章将介绍要求子序列必须是连续的情况下如何用算法解决最长公共子序列问题。
仍以上一章的两个字符串 “abcdea”和“aebcda”为例,如果子序列不要求连续,其最长公共子序列为“abcda”,如果子序列要求是连续,则其最长公共子序列应为“bcd”。在这种情况下,有可能两个字符串出现多个长度相同的公共子串,比如“askdfiryetd”和“trkdffirey”两个字符串就存在两个长度为3的公共子串,分别是“kdf”和“fir”,因此问题的性质发生了变化,需要找出两个字符串所有可能存在公共子串的情况,然后取最长的一个,如果有多个最长的公共子串,只取其中一个即可。
字符串 “abcdea”和“aebcda”如果都以最左端的a字符对齐,则能够匹配的最长公共子串就是“a”。但是如果用第二个字符串的e字符对齐第一个字符串的a字符,则能够匹配的最长公共子串就是“bcd”。可见,从两个字符串的不同位置开始对齐匹配,可以得到不同的结果,因此,本文采用的算法就是穷举两个字符串所有可能的对齐方式,对每种对齐方式进行字符的逐个匹配,找出最长的匹配子串。
一、 递归方法
首先看看递归方法。递归的方法比较简单,就是比较两个字符串的首字符是否相等,如果相等则将其添加到已知的公共子串结尾,然后对两个字符串去掉首字符后剩下的子串继续递归匹配。如果两个字符串的首字符不相等,则用三种对齐策略分别计算可能的最长公共子串,然后取最长的一个与当前已知的最长公共子串比较,如果比当前已知的最长公共子串长就用计算出的最长公共子串代替当前已知的最长公共子串。第一种策略是将第一个字符串的首字符删除,将剩下的子串与第二个字符串继续匹配;第二种策略是将第二个字符串的首字符删除,将剩下的子串与第一个字符串继续匹配;第三种策略是将两个字符串的首字符都删除,然后继续匹配两个字符串剩下的子串。删除首字符相当于字符对齐移位,整个算法实现如下:
180void RecursionLCS(const std::string& str1,
const std::string& str2, std::string& lcs)
181{
182
if(str1.length()
== 0
|| str2.length()
== 0)
183
return;
184
185
if(str1[0]
== str2[0])
186
{
187 lcs
+= str1[0];
188 RecursionLCS(str1.substr(1), str2.substr(1),
lcs);
189
}
190
else
191
{
192 std::string strTmp1,strTmp2,strTmp3;
193
194 RecursionLCS(str1.substr(1), str2,
strTmp1);
195 RecursionLCS(str1, str2.substr(1),
strTmp2);
196 RecursionLCS(str1.substr(1), str2.substr(1),
strTmp3);
197 std::string strLongest
= GetLongestString(strTmp1, strTmp2, strTmp3);
198
if(lcs.length()
< strLongest.length())
199 lcs
= strLongest;
200
}
201}
|
二、 两重循环方法
使用两重循环进行字符串的对齐匹配过程如下图所示:
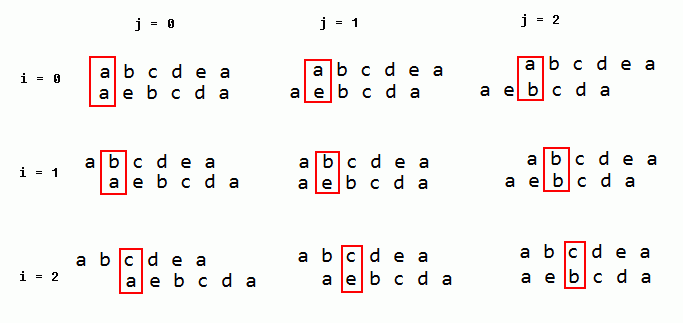
图(1)两重循环字符串对齐匹配示意图
第一重循环确定第一个字符串的对齐位置,第二重循环确定第二个字符串的对齐位置,每次循环确定一组两个字符串的对齐位置,并从此对齐位置开始匹配两个字符串的最长子串,如果匹配到的最长子串比已知的(由前面的匹配过程找到的)最长子串长,则更新已知最长子串的内容。两重循环的实现算法如下:
153void LoopLCS(const std::string& str1,
const std::string& str2, std::string& lcs)
154{
155 std::string::size_type i,j;
156
157
for(i =
0; i < str1.length(); i++)
158
{
159
for(j =
0; j < str2.length(); j++)
160
{
161 std::string lstr
= LeftAllignLongestSubString(str1.substr(i), str2.substr(j));
162
if(lstr.length()
> lcs.length())
163 lcs
= lstr;
164
}
165
}
166}
|
其中LeftAllignLongestSubString()函数的作用就是从某个对齐位置开始匹配最长公共子串,其实现过程就是逐个比较字符,并记录最长子串的位置信息。
三、 改进后的算法
使用两重循环的算法原理简单,LoopLCS()函数的实现也简单,时间复杂度为O(n2)(或O(mn)),比前一个递归算法的时间复杂度O(3n)要好很多。但是如果仔细观察图(1)所示的匹配示意图,就会发现这个算法在m x n次循环的过程中对同一位置的字符进行多次重复的比较。比如i=1,j=0的时候,从对齐位置开始第二次比较会比较第一个字符串的第三个字符“c”与第二个字符串的第二个字符“e”,而在i=1,j=0的时候,这个比较又进行了一次。全部比较的次数可以近似计算为mn(n-1)/2(其中m和n分别为两个字符串的长度),也就是说比较次数是O(n3)数量级的。而理论上两个字符串的不同位置都进行一次比较只需要mn次比较即可,也就是说比较次数的理论值应该是O(n2)数量级。
考虑对上述算法优化,可以将两个字符串每个位置上的字符的比较结果保存到一张二维表中,这张表中的[i,j]位置就表示第一个字符串的第i个字符与第二个字符串的第j个字符的比较结果,1表示字符相同,0表示字符不相同。在匹配最长子串的过程中,不必多次重复判断两个字符是否相等,只需从表中的[i,j]位置直接得到结果即可。
改进后的算法分成两个步骤:首先逐个比较两个字符串,建立关系二维表,然后用适当的方法搜索关系二维表,得到最长公共子串。第一个步骤比较简单,算法的改进主要集中在从关系二维表中得到最长公共子串的方法上。根据比较的原则,公共子串都是沿着二维表对角线方向出现的,对角线上连续出现1就表示这个位置是某次比较的公共子串。有上面的分析可知,只需要查找关系二维表中对角线上连续出现的1的个数,找出最长的一串1出现的位置,就可以得到两个字符串的最长公共子串。改进后的算法实现如下:
105void RelationLCS(const std::string& str1,
const std::string& str2, std::string& lcs)
106{
107
int d[MAX_STRING_LEN][MAX_STRING_LEN]
= {
0 };
108
int length = 0;
109
110 InitializeRelation(str1, str2, d);
111
int pos = GetLongestSubStringPosition(d, str1.length(), str2.length(),
&length);
112 lcs
= str1.substr(pos, length);
113}
|
InitializeRelation()函数就是初始化二维关系表,根据字符比较的结果将d[i,j]相应的位置置0或1,本文不再列出。算法改进的关键在GetLongestSubStringPosition()函数中,这个函数负责沿对角线搜索最长公共子串,并返回位置和长度信息。仍然以字符串 “abcdea”和“aebcda”为例,InitializeRelation()函数计算得到的关系表如图(2)所示:

图(2)示例字符串的位置关系示意图
从图(2)中可以看到,最长子串出现在红线标注的对角线上,起始位置在第一个字符串(纵向)中的位置是2,在第二个字符串(横向)中的位置是3,长度是3。搜索对角线从两个方向开始,一个是沿着纵向搜索左下角方向上的半个关系矩阵,另一个是沿着横向搜索右上角方向上的半个关系矩阵。对每个对角线分别查找连续的1出现的次数和位置,并比较得到连续1最多的位置。GetLongestSubStringPosition()函数的代码如下:
63int GetLongestSubStringPosition(int d[MAX_STRING_LEN][MAX_STRING_LEN],
int m,
int n, int
*length)
64{
65
int k,longestStart,longs;
66
int longestI = 0;
67
int longi = 0;
68
69
for(k =
0; k < n; k++)
70
{
71 longi
= GetLongestPosition(d, m, n,
0, k,
&longs);
72
if(longi > longestI)
73
{
74 longestI
= longi;
75 longestStart
= longs;
76
}
77
}
78
for(k =
1; k < m; k++)
79
{
80 longi
= GetLongestPosition(d, m, n, k,
0,
&longs);
81
if(longi > longestI)
82
{
83 longestI
= longi;
84 longestStart
= longs;
85
}
86
}
87
88
*length = longestI;
89
return longestStart;
90}
|
GetLongestPosition()函数就是沿着对角线方向搜索1出现的位置和连续长度,算法简单,本文不再列出。
至此,本文介绍了三种要求子串连续的情况下的求解最长公共子串的方法,都是简单易懂的方法,没有使用复杂的数学原理。第一种递归方法的时间复杂度是O(3n),这个时间复杂度的算法在问题规模比较大的情况下基本不具备可用性, 第三种方法是相对最好的方法,但是仍有改进的余地,比如使用位域数组,可以减少存储空间的使用,同时结合巧妙的位运算技巧,可以极大地提高GetLongestPosition()函数的效率。
参考资料:
【1】http://en.wikipedia.org/wiki/Longest_common_subsequence_problem
分享到:




相关推荐
算法系列之六:最长公共子序列(LCS)问题(连续子序列)的三种解法 本文档总结了解决最长公共子序列(LCS)问题的三种解法,针对连续子序列的情况。LCS 问题有两种定义子序列的方式:一是子序列不要求连续,二是子...
最长公共子序列(Longest Common Subsequence,简称LCS)是计算机科学中,尤其是在字符串处理、算法设计和分析领域的一个经典问题。这个问题的基本目标是找到两个字符串的最长子序列,这个子序列不需要连续,但必须...
最长公共子序列(Longest Common Subsequence,LCS)是计算机科学中一种经典的字符串问题,主要涉及算法设计和分析。它的目标是找到两个给定序列(通常为字符串)的最长子序列,该子序列在原序列中不需连续,但必须...
最长公共子序列(Longest Common Subsequence,LCS)是计算机科学中一种经典的字符串问题,主要应用于比较和分析两个或多个序列的相似性。在C++中实现LCS算法,通常采用动态规划的方法来解决。这里我们将深入探讨LCS...
最长公共子序列(Longest Common Subsequence,LCS)问题是计算机科学中一个经典的字符串处理问题,主要涉及到动态规划算法的应用。在这个问题中,目标是找到两个序列的最长子序列,这个子序列不必连续,但必须在原...
最长公共子序列(Longest Common Subsequence,LCS)是计算机科学中一种经典的字符串问题,主要涉及算法设计与分析,特别是在动态规划领域的应用。在这个问题中,我们需要找到两个或多个字符串之间的最长子序列,这...
最长公共子序列(Longest Common Subsequence,LCS)问题是一个经典的计算机科学问题,主要涉及到字符串处理和动态规划。在两个或多个字符串中找到的最长的子序列,它不一定是连续的,但在这个子序列中,每个字符都...
最长公共子序列(Longest Common Subsequence,LCS)问题是计算机科学中一个经典的字符串处理问题,它寻找两个序列之间的最长子序列,这个子序列不必连续但必须保持原序列的相对顺序。在本例中,提供的文件是使用C++...
最长公共子序列问题(LCS)是计算机科学中的一种基础问题,它在算法设计与分析领域占有重要地位。LCS问题主要解决的是如何找到两个序列共有的最长子序列的问题,该子序列在两个序列中出现的顺序一致,但不需要连续。...
最长公共子序列(Longest Common Subsequence,LCS)是计算机科学中一种经典的字符串问题,主要涉及算法设计与分析,特别是在动态规划领域的应用。LCS问题的目的是在两个或多个序列中找到最长的子序列,这个子序列并...
最长公共子序列(Longest Common Subsequence,LCS)问题是一个经典的计算机科学问题,主要涉及字符串处理和算法设计。在两个或多个字符串中找到一个最长的子序列,这个子序列不必连续,但必须保持原顺序。例如,...
最长公共子序列问题是一个经典的字符串处理问题,它要求找到两个或多个序列的最长子序列,这个子序列在每个序列中都存在,但不一定连续。例如,“ABCDGH”和“ACDFGHR”具有一个长度为3的LCS:“ADH”。这个问题可以...
1. **最长公共子序列(Longest Common Subsequence, LCS)** - LCS问题是寻找两个或多个序列中的最长子序列,这个子序列不必连续,但必须在原序列中都存在。 - 动态规划解法:定义一个二维数组dp[i][j]表示字符串...
在编程领域,字符串操作是常见任务之一,而寻找两个字符串的最长公共子序列(LCS)是其中的一个经典问题。LCS是指两个字符串中都出现过的最长的连续子序列,但不考虑字符在原始字符串中的相对位置。例如,字符串"ABC...
最长公共子序列(Longest Common Subsequence,LCS)是计算机科学中一种经典的问题,主要应用于文本比较、生物信息学等领域。在这个问题中,我们有两个字符串A和B,目标是找到它们的最长子序列,这个子序列不必是...
**最长公共子序列(Longest Common Subsequence, LCS)算法** 最长公共子序列问题是一个经典的计算机科学问题,它涉及到寻找两个或多个字符串之间的最长子序列,这个子序列并不需要连续,但必须保持原有的顺序。在...
在浙江工业大学的这个算法实验中,学生们通过两个具体问题——最长公共子序列问题和最大子段和问题——来学习和实践动态规划。 1. 最长公共子序列问题 最长公共子序列(Longest Common Subsequence, LCS)是寻找两...
根据给定的文件信息,我们可以总结出以下关于《算法导论》中动态规划与最长公共子序列(Longest Common Subsequence, LCS)的相关知识点: ### 动态规划概述 动态规划是一种解决多阶段决策问题的有效算法设计技术...
在信息技术领域,特别是在数据处理和算法设计中,Longest Common Subsequence(最长公共子序列,简称LCS)是一个经典的计算机科学问题。LCS算法广泛应用于序列比对、生物信息学、文本相似度计算等领域。本文件“一种...