数据库索引结构

数据库进阶系列之一：漫谈数据库索引

 

一、引言

对数据库索引的关注从未淡出我的们的讨论，那么数据库索引是什么样的？聚集索引与非聚集索引有什么不同？希望本文对各位同仁有一定的帮助。有不少存疑的地方，诚心希望各位不吝赐教指正，共同进步。[最近首页之争沸沸扬扬，也不知道这个放在这合适么，苦劳？功劳？……]

 

 

二、B-Tree

我们常见的数据库系统，其索引使用的数据结构多是B-Tree或者B+Tree。例如，MsSql使用的是B+Tree，Oracle及Sysbase使用的是B-Tree。所以在最开始，简单地介绍一下B-Tree。

 

B-Tree不同于Binary Tree（二叉树，最多有两个子树），一棵M阶的B-Tree满足以下条件：
1）每个结点至多有M个孩子；
2）除根结点和叶结点外，其它每个结点至少有M/2个孩子；
3）根结点至少有两个孩子（除非该树仅包含一个结点）；
4）所有叶结点在同一层，叶结点不包含任何关键字信息；
5）有K个关键字的非叶结点恰好包含K+1个孩子；

另外，对于一个结点，其内部的关键字是从小到大排序的。以下是B-Tree（M=4）的样例：

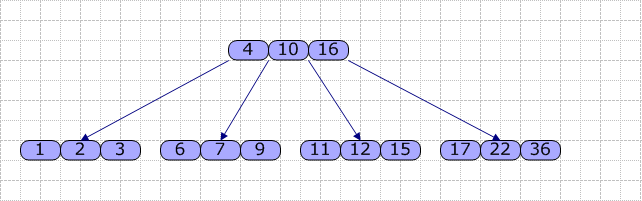
对于每个结点，主要包含一个关键字数组Key[]，一个指针数组（指向儿子）Son[]。在B-Tree内，查找的流程是：使用顺序查找（数组长度较短时）或折半查找方法查找Key[]数组，若找到关键字K，则返回该结点的地址及K在Key[]中的位置；否则，可确定K在某个Key[i]和Key[i+1]之间，则从Son[i]所指的子结点继续查找，直到在某结点中查找成功；或直至找到叶结点且叶结点中的查找仍不成功时，查找过程失败。

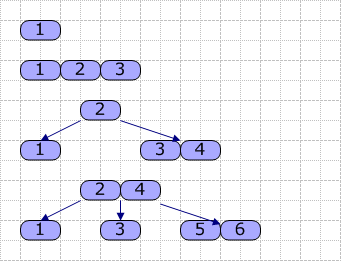
接着，我们使用以下图片演示如何生成B-Tree（M=4，依次插入1~6）：
从图可见，当我们插入关键字4时，由于原结点已经满了，故进行分裂，基本按一半的原则进行分裂，然后取出中间的关键字2，升级（这里是成为根结点）。其它的依类推，就是这样一个大概的过程。

 

三、数据库索引

1．什么是索引

在数据库中，索引的含义与日常意义上的“索引”一词并无多大区别（想想小时候查字典），它是用于提高数据库表数据访问速度的数据库对象。
A）索引可以避免全表扫描。多数查询可以仅扫描少量索引页及数据页，而不是遍历所有数据页。
B）对于非聚集索引，有些查询甚至可以不访问数据页。
C）聚集索引可以避免数据插入操作集中于表的最后一个数据页。
D）一些情况下，索引还可用于避免排序操作。

 

当然，众所周知，虽然索引可以提高查询速度，但是它们也会导致数据库系统更新数据的性能下降，因为大部分数据更新需要同时更新索引。

 

 

2.索引的存储

一条索引记录中包含的基本信息包括：键值（即你定义索引时指定的所有字段的值）+逻辑指针（指向数据页或者另一索引页）。

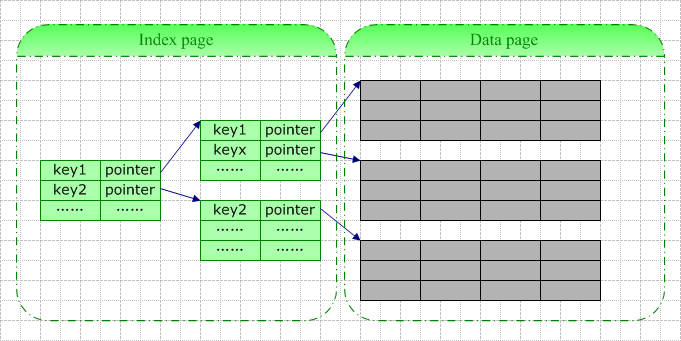
当你为一张空表创建索引时，数据库系统将为你分配一个索引页，该索引页在你插入数据前一直是空的。此页此时既是根结点，也是叶结点。每当你往表中插入一行数据，数据库系统即向此根结点中插入一行索引记录。当根结点满时，数据库系统大抵按以下步骤进行分裂：
A）创建两个儿子结点
B）将原根结点中的数据近似地拆成两半，分别写入新的两个儿子结点
C）根结点中加上指向两个儿子结点的指针

 

通常状况下，由于索引记录仅包含索引字段值（以及4-9字节的指针），索引实体比真实的数据行要小许多，索引页相较数据页来说要密集许多。一个索引页可以存储数量更多的索引记录，这意味着在索引中查找时在I/O上占很大的优势，理解这一点有助于从本质上了解使用索引的优势。

 

 

3．索引的类型

A）聚集索引，表数据按照索引的顺序来存储的。对于聚集索引，叶子结点即存储了真实的数据行，不再有另外单独的数据页。
B）非聚集索引，表数据存储顺序与索引顺序无关。对于非聚集索引，叶结点包含索引字段值及指向数据页数据行的逻辑指针，该层紧邻数据页，其行数量与数据表行数据量一致。

 

在一张表上只能创建一个聚集索引，因为真实数据的物理顺序只可能是一种。如果一张表没有聚集索引，那么它被称为“堆集”（Heap）。这样的表中的数据行没有特定的顺序，所有的新行将被添加的表的末尾位置。

 

 

4．聚集索引

在聚集索引中，叶结点也即数据结点，所有数据行的存储顺序与索引的存储顺序一致。

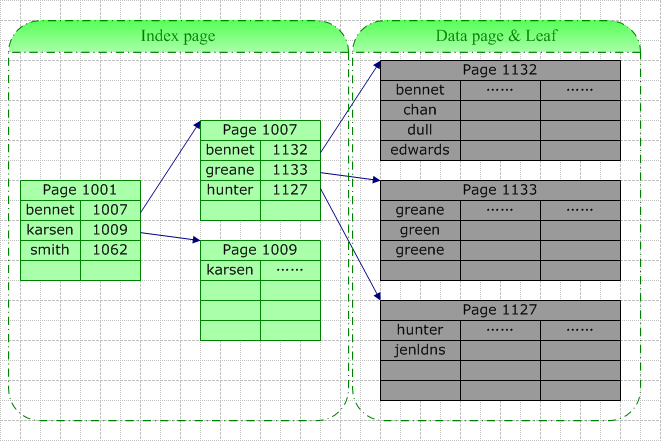
1）聚集索引与查询操作

如上图，我们在名字字段上建立聚集索引，当需要在根据此字段查找特定的记录时，数据库系统会根据特定的系统表查找的此索引的根，然后根据指针查找下一个，直到找到。例如我们要查询“Green”，由于它介于[Bennet,Karsen]，据此我们找到了索引页1007，在该页中“Green”介于[Greane, Hunter]间，据此我们找到叶结点1133（也即数据结点），并最终在此页中找以了目标数据行。

 

此次查询的IO包括3个索引页的查询（其中最后一次实际上是在数据页中查询）。这里的查找可能是从磁盘读取(Physical Read)或是从缓存中读取(Logical Read)，如果此表访问频率较高，那么索引树中较高层的索引很可能在缓存中被找到。所以真正的IO可能小于上面的情况。

 

 

2）聚集索引与插入操作

最简单的情况下，插入操作根据索引找到对应的数据页，然后通过挪动已有的记录为新数据腾出空间，最后插入数据。

 

如果数据页已满，则需要拆分数据页（页拆分是一种耗费资源的操作，一般数据库系统中会有相应的机制要尽量减少页拆分的次数，通常是通过为每页预留空间来实现）：
A）在该使用的数据段（extent）上分配新的数据页，如果数据段已满，则需要分配新段。
B）调整索引指针，这需要将相应的索引页读入内存并加锁。
C）大约有一半的数据行被归入新的数据页中。
D）如果表还有非聚集索引，则需要更新这些索引指向新的数据页。

 

特殊情况：
A）如果新插入的一条记录包含很大的数据，可能会分配两个新数据页，其中之一用来存储新记录，另一存储从原页中拆分出来的数据。
B）通常数据库系统中会将重复的数据记录存储于相同的页中。
C）类似于自增列为聚集索引的，数据库系统可能并不拆分数据页，页只是简单的新添数据页。

 

 

3）聚集索引与删除操作

删除行将导致其下方的数据行向上移动以填充删除记录造成的空白。

如果删除的行是该数据页中的最后一行，那么该数据页将被回收，相应的索引页中的记录将被删除。如果回收的数据页位于跟该表的其它数据页相同的段上，那么它可能在随后的时间内被利用。如果该数据页是该段的唯一一个数据页，则该段也被回收。

 

对于数据的删除操作，可能导致索引页中仅有一条记录，这时，该记录可能会被移至邻近的索引页中，原索引页将被回收，即所谓的“索引合并”。

 

 

5．非聚集索引

非聚集索引与聚集索引相比：
A）叶子结点并非数据结点
B）叶子结点为每一真正的数据行存储一个“键-指针”对
C）叶子结点中还存储了一个指针偏移量，根据页指针及指针偏移量可以定位到具体的数据行。
D）类似的，在除叶结点外的其它索引结点，存储的也是类似的内容，只不过它是指向下一级的索引页的。

 

聚集索引是一种稀疏索引，数据页上一级的索引页存储的是页指针，而不是行指针。而对于非聚集索引，则是密集索引，在数据页的上一级索引页它为每一个数据行存储一条索引记录。

 

对于根与中间级的索引记录，它的结构包括：
A）索引字段值
B）RowId（即对应数据页的页指针+指针偏移量）。在高层的索引页中包含RowId是为了当索引允许重复值时，当更改数据时精确定位数据行。
C）下一级索引页的指针

 

对于叶子层的索引对象，它的结构包括：
A）索引字段值
B）RowId

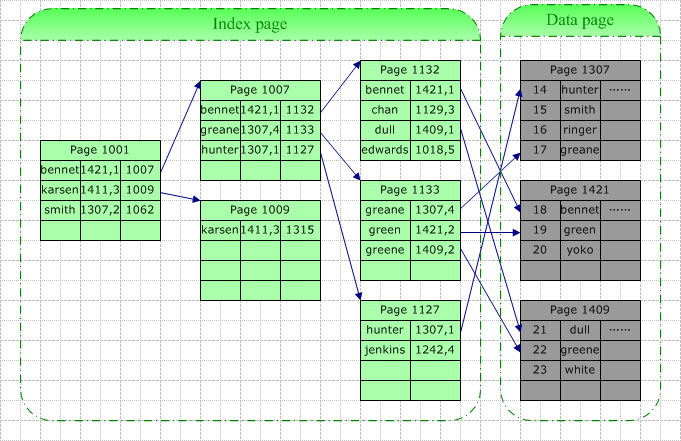
1）非聚集索引与查询操作

针对上图，如果我们同样查找“Green”，那么一次查询操作将包含以下IO：3个索引页的读取+1个数据页的读取。同样，由于缓存的关系，真实的IO实际可能要小于上面列出的。

 

 

2）非聚集索引与插入操作

如果一张表包含一个非聚集索引但没有聚集索引，则新的数据将被插入到最末一个数据页中，然后非聚集索引将被更新。如果也包含聚集索引，该聚集索引将被用于查找新行将要处于什么位置，随后，聚集索引、以及非聚集索引将被更新。

 

 

3）非聚集索引与删除操作

如果在删除命令的Where子句中包含的列上，建有非聚集索引，那么该非聚集索引将被用于查找数据行的位置，数据删除之后，位于索引叶子上的对应记录也将被删除。如果该表上有其它非聚集索引，则它们叶子结点上的相应数据也要删除。

 

如果删除的数据是该数所页中的唯一一条，则该页也被回收，同时需要更新各个索引树上的指针。

 

由于没有自动的合并功能，如果应用程序中有频繁的随机删除操作，最后可能导致表包含多个数据页，但每个页中只有少量数据。

 

 

6．索引覆盖

索引覆盖是这样一种索引策略：当某一查询中包含的所需字段皆包含于一个索引中，此时索引将大大提高查询性能。

 

包含多个字段的索引，称为复合索引。索引最多可以包含31个字段，索引记录最大长度为600B。如果你在若干个字段上创建了一个复合的非聚集索引，且你的查询中所需Select字段及Where,Order By,Group By,Having子句中所涉及的字段都包含在索引中，则只搜索索引页即可满足查询，而不需要访问数据页。由于非聚集索引的叶结点包含所有数据行中的索引列值，使用这些结点即可返回真正的数据，这种情况称之为“索引覆盖”。

 

在索引覆盖的情况下，包含两种索引扫描：
A）匹配索引扫描
B）非匹配索引扫描

 

 

1）匹配索引扫描

此类索引扫描可以让我们省去访问数据页的步骤，当查询仅返回一行数据时，性能提高是有限的，但在范围查询的情况下，性能提高将随结果集数量的增长而增长。

 

针对此类扫描，索引必须包含查询中涉及的的所有字段，另外，还需要满足：Where子句中包含索引中的“引导列”（Leading Column），例如一个复合索引包含A,B,C,D四列，则A为“引导列”。如果Where子句中所包含列是BCD或者BD等情况，则只能使用非匹配索引扫描。

 

 

2）非配置索引扫描

正如上述，如果Where子句中不包含索引的导引列，那么将使用非配置索引扫描。这最终导致扫描索引树上的所有叶子结点，当然，它的性能通常仍强于扫描所有的数据页。 

 

原文 http://www.cnblogs.com/KissKnife/archive/2009/03/30/1425534.html