原文:http://blog.csdn.net/pzhtpf/article/details/7560312
好东西,值得收藏
前几天,看到一篇前辈的博文“程序员必知的8大排序”,不禁的手痒起来,重新翻开严蔚敏老师的《数据结构》复习了一遍,然后一一的用java去实现,其中有不足之处,还望各位道友指正出来。
先来看看8种排序之间的关系:
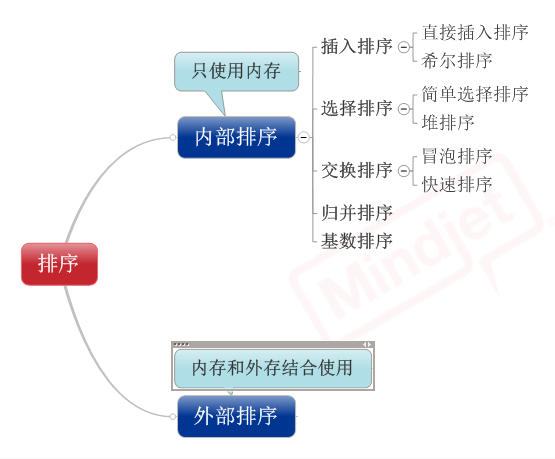
1,
直接插入排序
(1)基本思想:在要排序的一组数中,假设前面(n-1) [n>=2] 个数已经是排
好顺序的,现在要把第n个数插到前面的有序数中,使得这n个数
也是排好顺序的。如此反复循环,直到全部排好顺序。
(2)实例
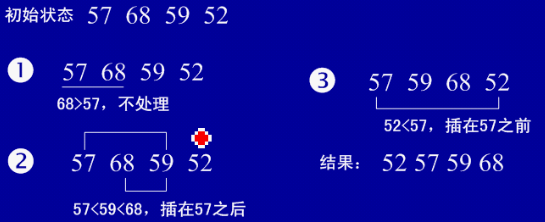
(3)用java实现
package com.njue;
publicclass insertSort {
public insertSort(){
int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};
int temp=0;
for(int i=1;i<a.length;i++){
int j=i-1;
temp=a[i];
for(;j>=0&&temp<a[j];j--){
a[j+1]=a[j]; //将大于temp的值整体后移一个单位
}
a[j+1]=temp;
}
for(int i=0;i<a.length;i++)
System.out.println(a[i]);
}
}
2,
希尔排序(最小增量排序)
(1)基本思想:算法先将要排序的一组数按某个增量d(n/2,n为要排序数的个数)分成若干组,每组中记录的下标相差d.对每组中全部元素进行直接插入排序,然后再用一个较小的增量(d/2)对它进行分组,在每组中再进行直接插入排序。当增量减到1时,进行直接插入排序后,排序完成。
(2)实例:
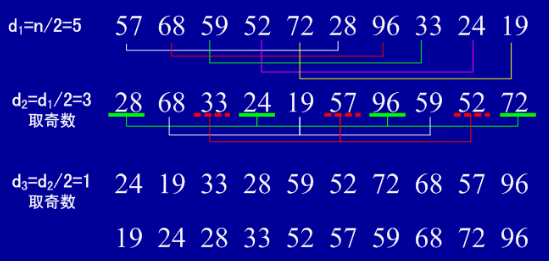
(3)用java实现
publicclass shellSort {
publicshellSort(){
int a[]={1,54,6,3,78,34,12,45,56,100};
double d1=a.length;
int temp=0;
while(true){
d1= Math.ceil(d1/2);
int d=(int) d1;
for(int x=0;x<d;x++){
for(int i=x+d;i<a.length;i+=d){
int j=i-d;
temp=a[i];
for(;j>=0&&temp<a[j];j-=d){
a[j+d]=a[j];
}
a[j+d]=temp;
}
}
if(d==1)
break;
}
for(int i=0;i<a.length;i++)
System.out.println(a[i]);
}
}
程序员必知的8大排序(二)-------简单选择排序,堆排序(java实现)
3.简单选择排序
(1)基本思想:在要排序的一组数中,选出最小的一个数与第一个位置的数交换;
然后在剩下的数当中再找最小的与第二个位置的数交换,如此循环到倒数第二个数和最后一个数比较为止。
(2)实例:

(3)用java实现
4,堆排序
(1)基本思想:堆排序是一种树形选择排序,是对直接选择排序的有效改进。
堆的定义如下:具有n个元素的序列(h1,h2,...,hn),当且仅当满足(hi>=h2i,hi>=2i+1)或(hi<=h2i,hi<=2i+1)(i=1,2,...,n/2)时称之为堆。在这里只讨论满足前者条件的堆。由堆的定义可以看出,堆顶元素(即第一个元素)必为最大项(大顶堆)。完全二叉树可以很直观地表示堆的结构。堆顶为根,其它为左子树、右子树。初始时把要排序的数的序列看作是一棵顺序存储的二叉树,调整它们的存储序,使之成为一个堆,这时堆的根节点的数最大。然后将根节点与堆的最后一个节点交换。然后对前面(n-1)个数重新调整使之成为堆。依此类推,直到只有两个节点的堆,并对它们作交换,最后得到有n个节点的有序序列。从算法描述来看,堆排序需要两个过程,一是建立堆,二是堆顶与堆的最后一个元素交换位置。所以堆排序有两个函数组成。一是建堆的渗透函数,二是反复调用渗透函数实现排序的函数。
(2)实例:
初始序列:46,79,56,38,40,84
建堆:
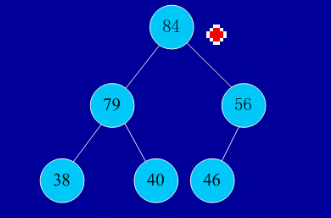
交换,从堆中踢出最大数
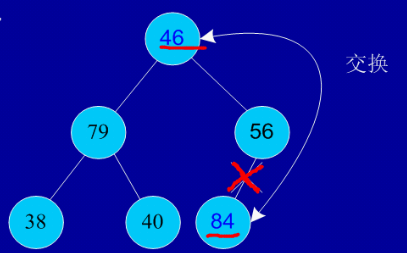
剩余结点再建堆,再交换踢出最大数
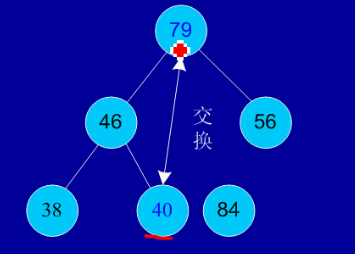
依次类推:最后堆中剩余的最后两个结点交换,踢出一个,排序完成。
(3)用java实现
import java.util.Arrays;
publicclass HeapSort {
inta[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};
public HeapSort(){
heapSort(a);
}
public void heapSort(int[] a){
System.out.println("开始排序");
int arrayLength=a.length;
//循环建堆
for(int i=0;i<arrayLength-1;i++){
//建堆
buildMaxHeap(a,arrayLength-1-i);
//交换堆顶和最后一个元素
swap(a,0,arrayLength-1-i);
System.out.println(Arrays.toString(a));
}
}
private void swap(int[] data, int i, int j) {
// TODO Auto-generated method stub
int tmp=data[i];
data[i]=data[j];
data[j]=tmp;
}
//对data数组从0到lastIndex建大顶堆
privatevoid buildMaxHeap(int[] data, int lastIndex) {
// TODO Auto-generated method stub
//从lastIndex处节点(最后一个节点)的父节点开始
for(int i=(lastIndex-1)/2;i>=0;i--){
//k保存正在判断的节点
int k=i;
//如果当前k节点的子节点存在
while(k*2+1<=lastIndex){
//k节点的左子节点的索引
int biggerIndex=2*k+1;
//如果biggerIndex小于lastIndex,即biggerIndex+1代表的k节点的右子节点存在
if(biggerIndex<lastIndex){
//若果右子节点的值较大
if(data[biggerIndex]<data[biggerIndex+1]){
//biggerIndex总是记录较大子节点的索引
biggerIndex++;
}
}
//如果k节点的值小于其较大的子节点的值
if(data[k]<data[biggerIndex]){
//交换他们
swap(data,k,biggerIndex);
//将biggerIndex赋予k,开始while循环的下一次循环,重新保证k节点的值大于其左右子节点的值
k=biggerIndex;
}else{
break;
}
}
}
}
}
5.冒泡排序
(1)基本思想:在要排序的一组数中,对当前还未排好序的范围内的全部数,自上而下对相邻的两个数依次进行比较和调整,让较大的数往下沉,较小的往上冒。即:每当两相邻的数比较后发现它们的排序与排序要求相反时,就将它们互换。
(2)实例:

(3)用java实现
publi cclass bubbleSort {
public bubbleSort(){
int a[]={1,54,6,3,78,34,12,45};
int temp=0;
for(int i=0;i<a.length;i++){
for(int j=i+1;j<a.length;j++){
if(a[i]>a[j]){
temp=a[i];
a[i]=a[j];
a[j]=temp;
}
}
}
for(int i=0;i<a.length;i++)
System.out.println(a[i]);
}
}
经过道友的提醒,发现上面的不是正宗的冒泡排序,所以更正过来:
正宗的冒泡排序:
public class bubbleSort {
public bubbleSort(){
int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};
int temp=0;
for(int i=0;i<a.length-1;i++){
for(int j=0;j<a.length-1-i;j++){
if(a[j]>a[j+1]){
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
}
for(int i=0;i<a.length;i++)
System.out.println(a[i]);
}
}
但第一种是什么排序呢?跟选择排序有点类似,但又不是,还望高手指点一二!
6.快速排序
(1)基本思想:选择一个基准元素,通常选择第一个元素或者最后一个元素,通过一趟扫描,将待排序列分成两部分,一部分比基准元素小,一部分大于等于基准元素,此时基准元素在其排好序后的正确位置,然后再用同样的方法递归地排序划分的两部分。
(2)实例:

(3)用java实现
public class quickSort {
inta[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};
public quickSort(){
quick(a);
for(int i=0;i<a.length;i++)
System.out.println(a[i]);
}
publicint getMiddle(int[] list, int low, int high) {
int tmp = list[low]; //数组的第一个作为中轴
while (low < high) {
while (low < high && list[high] >= tmp) {
high--;
}
list[low] = list[high]; //比中轴小的记录移到低端
while (low < high && list[low] <= tmp) {
low++;
}
list[high] = list[low]; //比中轴大的记录移到高端
}
list[low] = tmp; //中轴记录到尾
return low; //返回中轴的位置
}
publicvoid _quickSort(int[] list, int low, int high) {
if (low < high) {
int middle = getMiddle(list, low, high); //将list数组进行一分为二
_quickSort(list, low, middle - 1); //对低字表进行递归排序
_quickSort(list, middle + 1, high); //对高字表进行递归排序
}
}
publicvoid quick(int[] a2) {
if (a2.length > 0) { //查看数组是否为空
_quickSort(a2, 0, a2.length - 1);
}
}
}
7、归并排序
(1)基本排序:归并(Merge)排序法是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
(2)实例:

(3)用java实现
import java.util.Arrays;
public class mergingSort {
int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};
public mergingSort(){
sort(a,0,a.length-1);
for(int i=0;i<a.length;i++)
System.out.println(a[i]);
}
public void sort(int[] data, int left, int right) {
// TODO Auto-generated method stub
if(left<right){
//找出中间索引
int center=(left+right)/2;
//对左边数组进行递归
sort(data,left,center);
//对右边数组进行递归
sort(data,center+1,right);
//合并
merge(data,left,center,right);
}
}
public void merge(int[] data, int left, int center, int right) {
// TODO Auto-generated method stub
int [] tmpArr=new int[data.length];
int mid=center+1;
//third记录中间数组的索引
int third=left;
int tmp=left;
while(left<=center&&mid<=right){
//从两个数组中取出最小的放入中间数组
if(data[left]<=data[mid]){
tmpArr[third++]=data[left++];
}else{
tmpArr[third++]=data[mid++];
}
}
//剩余部分依次放入中间数组
while(mid<=right){
tmpArr[third++]=data[mid++];
}
while(left<=center){
tmpArr[third++]=data[left++];
}
//将中间数组中的内容复制回原数组
while(tmp<=right){
data[tmp]=tmpArr[tmp++];
}
System.out.println(Arrays.toString(data));
}
}
(1)基本思想:将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。
(2)实例:
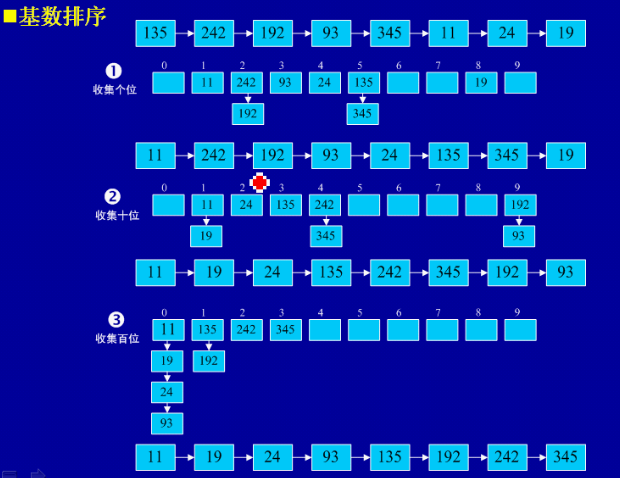
(3)用java实现
import java.util.ArrayList;
import java.util.List;
public class radixSort {
int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,101,56,17,18,23,34,15,35,25,53,51};
public radixSort(){
sort(a);
for(int i=0;i<a.length;i++)
System.out.println(a[i]);
}
public void sort(int[] array){
//首先确定排序的趟数;
int max=array[0];
for(int i=1;i<array.length;i++){
if(array[i]>max){
max=array[i];
}
}
int time=0;
//判断位数;
while(max>0){
max/=10;
time++;
}
//建立10个队列;
List<ArrayList> queue=new ArrayList<ArrayList>();
for(int i=0;i<10;i++){
ArrayList<Integer> queue1=new ArrayList<Integer>();
queue.add(queue1);
}
//进行time次分配和收集;
for(int i=0;i<time;i++){
//分配数组元素;
for(int j=0;j<array.length;j++){
//得到数字的第time+1位数;
int x=array[j]%(int)Math.pow(10, i+1)/(int)Math.pow(10, i);
ArrayList<Integer> queue2=queue.get(x);
queue2.add(array[j]);
queue.set(x, queue2);
}
int count=0;//元素计数器;
//收集队列元素;
for(int k=0;k<10;k++){
while(queue.get(k).size()>0){
ArrayList<Integer> queue3=queue.get(k);
array[count]=queue3.get(0);
queue3.remove(0);
count++;
}
}
}
}
}
分享到:




















相关推荐
在编程领域,排序算法是基础且重要的概念,对于Java程序员来说,理解并掌握各种排序算法能提升编程能力。以下是8种常见的排序算法及其基本思想、实现方式的详细解释: 1. 直接插入排序: - 基本思想:将未排序的...
Java程序员必知的8大排序.doc,以前学习时找的,分享给热爱java的初学者们学习参考。
Java程序员在日常开发中,掌握各种排序算法是提高效率、优化代码的关键。以下是对Java排序算法的详细解析,包括直接插入排序、希尔排序和简单选择排序。 1. 直接插入排序 直接插入排序是一种简单直观的排序算法,它...
### 知识点一:直接插入排序 #### 基本思想 ...以上四种排序算法是程序员必须掌握的基本排序方法,每种算法都有其适用场景和优缺点。理解这些排序算法的工作原理对于优化程序性能、提高编程技能都至关重要。
### 程序员必知的八大排序三大查找 #### 排序算法概览 排序算法是计算机科学中的一项基础技能,对数据进行排序能够帮助我们更高效地处理信息。以下将详细介绍八种常见的排序算法及其特点。 #### 1. 直接插入排序 ...
本文将深入探讨Java程序员必须了解的八大排序算法,这些算法不仅对于提升编程能力,理解数据结构与算法有着重要作用,同时也是面试中常考的热点。以下是这八大排序算法的详解: 1. 冒泡排序(Bubble Sort) 冒泡...
Java 程序员必知的 8 大排序 在 Java 语言中,排序算法是非常重要的一部分,以下是 8 种排序算法的基本思想、实例和 Java 实现: 1. 直接插入排序 基本思想:在要排序的一组数中,假设前面(n-1)[n>=2] 个数已经...
程序员在日常工作中,掌握高效的排序算法是至关重要的。本文主要探讨了两种常见的排序算法:直接插入排序和希尔排序,这两种算法都是基于比较的排序方法,适用于不同规模和数据特性的数组。 1. **直接插入排序**: ...
在编程领域,排序是至关重要的基础操作,尤其是在...而堆排序虽然比选择排序复杂,但其时间复杂度为O(n log n),更适合处理大数据量的排序任务。在实际应用中,根据数据规模和性能需求,开发者会选择合适的排序算法。
下面将详细介绍一些程序员必知的Excel操作,帮助提升工作效率。 1. 数据整理: - **排序与筛选**:对数据进行升序或降序排列,利用条件筛选找出特定数据。 - **合并单元格**:在报表头部创建合并的标题,注意合并...
Java编程语言中的排序算法是程序员必须掌握的重要技能之一。在Java中实现排序算法可以极大地提升程序的效率和性能。这里我们讨论的是Java中常见的三种排序算法:直接插入排序、希尔排序和简单选择排序。 1. 直接...
- 快速排序广泛应用于各种数据处理场景,特别是在大数据集的排序中表现出色。 - 在需要高效排序且内存空间足够的情况下,快速排序是一个很好的选择。 ### 知识点二:堆排序算法 **定义与特性:** 堆排序是一种基于...
每天都在叫嚣自己会什么技术,什么框架,可否意识到你每天都在被这些新名词、新技术所迷惑,.NET、XML等等技术固然诱人,可是如果自己的基础不...废话不多说,本文要介绍的这些排序算法就是基础中的基础,程序员必知!
"程序员必知必会经典算法"这个主题涵盖了编程领域中的重要概念,包括基础算法和数据结构,这些都是C、C++等语言中不可或缺的部分。下面将详细讨论这些经典算法及其在实际编程中的应用。 首先,我们要理解什么是算法...
《程序员必知的硬核知识大全》是一份涵盖了IT行业核心知识的综合资源,旨在帮助程序员提升技能,增强职业竞争力。这份压缩包包含了一个名为"程序员必知的硬核知识大全.pdf"的文件,它详细阐述了编程、算法、数据结构...
标题和描述中提到的知识点是IT领域中程序员必须掌握的基础算法——八大排序算法和三大查找算法。这些算法是数据处理和程序优化的核心,对于提升软件性能至关重要。下面将详细介绍这八大排序算法及其特点: 1. **...
本资源“GitHub优质项目汇总——程序员必知.zip”是针对程序员精心筛选的一系列优秀项目集合,涵盖多个领域,旨在帮助提升技能,增强学习效率。 首先,让我们关注“测试”这一标签。在软件开发过程中,测试是确保...
冒泡排序是一种简单的排序算法,通过不断交换相邻的不正确顺序的元素,逐渐将较大的元素“冒”到数组的后端,时间复杂度为O(n^2)。 6. **选择排序**: 选择排序每次找到当前未排序部分的最小(或最大)元素,放到...
20非常有用的java程序片,dom4j生产xml,java enum,for循环,java向oracle 插入百万数据,程序员必知8大排序,map的三种遍历....就是我自己平时在学习的时候遇到的问题然后在网上的找到相关解决方法。