ن¸»è¦پن»‹ç»چMP(Matching Pursuits)ç®—و³•ه’ŒOMP(Orthogonal Matching Pursuit)ç®—و³•[1],è؟™ن¸¤ن¸ھç®—و³•è™½ç„¶هœ¨90ه¹´ن»£هˆه°±وڈگه‡؛و¥ن؛†ï¼Œن½†ن½œن¸؛ç»ڈه…¸çڑ„ç®—و³•ï¼Œه›½ه†…و–‡çŒ®(هڈ¯èƒ½وœ‰وˆ‘و²،وœ‰وگœç´¢هˆ°)都ن»…وڈڈè؟°ن؛†ç®—و³•و¥éھ¤ه’Œç®€هچ•çڑ„ه؛”用,ه¹¶وœھه¯¹ه…¶è؟›è،Œè¯¦ه°½çڑ„هˆ†وگ,ه›½ه¤–çڑ„و–‡çŒ®è؟کوک¯هˆ†وگçڑ„ه¾ˆé€ڈه½»ï¼Œو‰€ن»¥وˆ‘结هگˆè‡ھه·±çڑ„çگ†è§£ï¼Œو¥هˆ†وگن¸€ن¸‹ه†™هˆ°هچڑه®¢é‡Œï¼Œç®—ن½œç¬”è®°م€‚
1. ن؟،هڈ·çڑ„稀ç–ڈè،¨ç¤؛(sparse representation of signals)
ç»™ه®ڑن¸€ن¸ھè؟‡ه®Œه¤‡ه—ه…¸çں©éکµ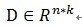 ,ه…¶ن¸ه®ƒçڑ„و¯ڈهˆ—è،¨ç¤؛ن¸€ç§چهژںه‹ن؟،هڈ·çڑ„هژںهگم€‚ç»™ه®ڑن¸€ن¸ھن؟،هڈ·y,ه®ƒهڈ¯ن»¥è¢«è،¨ç¤؛وˆگè؟™ن؛›هژںهگçڑ„稀ç–ڈç؛؟و€§ç»„هگˆم€‚ن؟،هڈ· y هڈ¯ن»¥è¢«è،¨è¾¾ن¸؛ y = Dx ,وˆ–者
,ه…¶ن¸ه®ƒçڑ„و¯ڈهˆ—è،¨ç¤؛ن¸€ç§چهژںه‹ن؟،هڈ·çڑ„هژںهگم€‚ç»™ه®ڑن¸€ن¸ھن؟،هڈ·y,ه®ƒهڈ¯ن»¥è¢«è،¨ç¤؛وˆگè؟™ن؛›هژںهگçڑ„稀ç–ڈç؛؟و€§ç»„هگˆم€‚ن؟،هڈ· y هڈ¯ن»¥è¢«è،¨è¾¾ن¸؛ y = Dx ,وˆ–者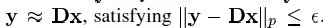 م€‚
ه—ه…¸çں©éکµن¸و‰€è°“è؟‡ه®Œه¤‡و€§ï¼ŒوŒ‡çڑ„وک¯هژںهگçڑ„ن¸ھو•°è؟œè؟œه¤§ن؛ژن؟،هڈ·yçڑ„é•؟ه؛¦(ه…¶é•؟ه؛¦ه¾ˆوک¾ç„¶وک¯n),هچ³n<<kم€‚
م€‚
ه—ه…¸çں©éکµن¸و‰€è°“è؟‡ه®Œه¤‡و€§ï¼ŒوŒ‡çڑ„وک¯هژںهگçڑ„ن¸ھو•°è؟œè؟œه¤§ن؛ژن؟،هڈ·yçڑ„é•؟ه؛¦(ه…¶é•؟ه؛¦ه¾ˆوک¾ç„¶وک¯n),هچ³n<<kم€‚
2.MPç®—و³•(هŒ¹é…چè؟½è¸ھç®—و³•)
2.1 ç®—و³•وڈڈè؟°
ن½œن¸؛ه¯¹ن؟،هڈ·è؟›è،Œç¨€ç–ڈهˆ†è§£çڑ„و–¹و³•ن¹‹ن¸€ï¼Œه°†ن؟،هڈ·هœ¨ه®Œه¤‡ه—ه…¸ه؛“ن¸ٹè؟›è،Œهˆ†è§£م€‚
هپ‡ه®ڑ被è،¨ç¤؛çڑ„ن؟،هڈ·ن¸؛y,ه…¶é•؟ه؛¦ن¸؛nم€‚هپ‡ه®ڑHè،¨ç¤؛Hilbertç©؛间,هœ¨è؟™ن¸ھç©؛é—´H里,由ن¸€ç»„هگ‘é‡ڈ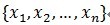 و„وˆگه—ه…¸çں©éکµD,ه…¶ن¸و¯ڈن¸ھهگ‘é‡ڈهڈ¯ن»¥ç§°ن¸؛هژںهگ(atom),ه…¶é•؟ه؛¦ن¸ژ被è،¨ç¤؛ن؟،هڈ· y çڑ„é•؟ه؛¦n相هگŒï¼Œè€Œن¸”è؟™ن؛›هگ‘é‡ڈه·²ن½œن¸؛ه½’ن¸€هŒ–ه¤„çگ†ï¼Œهچ³|
و„وˆگه—ه…¸çں©éکµD,ه…¶ن¸و¯ڈن¸ھهگ‘é‡ڈهڈ¯ن»¥ç§°ن¸؛هژںهگ(atom),ه…¶é•؟ه؛¦ن¸ژ被è،¨ç¤؛ن؟،هڈ· y çڑ„é•؟ه؛¦n相هگŒï¼Œè€Œن¸”è؟™ن؛›هگ‘é‡ڈه·²ن½œن¸؛ه½’ن¸€هŒ–ه¤„çگ†ï¼Œهچ³|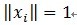 ,ن¹ںه°±وک¯هچ•ن½چهگ‘é‡ڈé•؟ه؛¦ن¸؛1م€‚MPç®—و³•çڑ„هں؛وœ¬و€وƒ³ï¼ڑن»ژه—ه…¸çں©éکµD(ن¹ں称ن¸؛è؟‡ه®Œه¤‡هژںهگه؛“ن¸ï¼‰ï¼Œé€‰و‹©ن¸€ن¸ھن¸ژن؟،هڈ·
y وœ€هŒ¹é…چçڑ„هژںهگ(ن¹ںه°±وک¯وںگهˆ—),و„ه»؛ن¸€ن¸ھ稀ç–ڈ逼è؟‘,ه¹¶و±‚ه‡؛ن؟،هڈ·و®‹ه·®ï¼Œç„¶هگژ继ç»é€‰و‹©ن¸ژن؟،هڈ·و®‹ه·®وœ€هŒ¹é…چçڑ„هژںهگ,هڈچه¤چè؟ن»£ï¼Œن؟،هڈ·yهڈ¯ن»¥ç”±è؟™ن؛›هژںهگو¥ç؛؟و€§ه’Œï¼Œه†چهٹ ن¸ٹوœ€هگژçڑ„و®‹ه·®ه€¼و¥è،¨ç¤؛م€‚ه¾ˆوک¾ç„¶ï¼Œه¦‚وœو®‹ه·®ه€¼هœ¨هڈ¯ن»¥ه؟½ç•¥çڑ„范ه›´ه†…,هˆ™ن؟،هڈ·yه°±وک¯è؟™ن؛›هژںهگçڑ„ç؛؟و€§ç»„هگˆم€‚ه¦‚وœé€‰و‹©ن¸ژن؟،هڈ·yوœ€هŒ¹é…چçڑ„هژںهگï¼ںه¦‚ن½•و„ه»؛稀ç–ڈ逼è؟‘ه¹¶و±‚و®‹ه·®ï¼ںه¦‚ن½•è؟›è،Œè؟ن»£ï¼ںوˆ‘ن»¬و¥è¯¦ç»†ن»‹ç»چن½؟用MPè؟›è،Œن؟،هڈ·هˆ†è§£çڑ„و¥éھ¤ï¼ڑ[1] è®،ç®—ن؟،هڈ· y ن¸ژه—ه…¸çں©éکµن¸و¯ڈهˆ—(هژںهگ)çڑ„ه†…积,选و‹©ç»ه¯¹ه€¼وœ€ه¤§çڑ„ن¸€ن¸ھهژںهگ,ه®ƒه°±وک¯ن¸ژن؟،هڈ· y هœ¨وœ¬و¬،è؟ن»£è؟گç®—ن¸وœ€هŒ¹é…چçڑ„م€‚用ن¸“ن¸ڑوœ¯è¯و¥وڈڈè؟°ï¼ڑن»¤ن؟،هڈ·
,ن¹ںه°±وک¯هچ•ن½چهگ‘é‡ڈé•؟ه؛¦ن¸؛1م€‚MPç®—و³•çڑ„هں؛وœ¬و€وƒ³ï¼ڑن»ژه—ه…¸çں©éکµD(ن¹ں称ن¸؛è؟‡ه®Œه¤‡هژںهگه؛“ن¸ï¼‰ï¼Œé€‰و‹©ن¸€ن¸ھن¸ژن؟،هڈ·
y وœ€هŒ¹é…چçڑ„هژںهگ(ن¹ںه°±وک¯وںگهˆ—),و„ه»؛ن¸€ن¸ھ稀ç–ڈ逼è؟‘,ه¹¶و±‚ه‡؛ن؟،هڈ·و®‹ه·®ï¼Œç„¶هگژ继ç»é€‰و‹©ن¸ژن؟،هڈ·و®‹ه·®وœ€هŒ¹é…چçڑ„هژںهگ,هڈچه¤چè؟ن»£ï¼Œن؟،هڈ·yهڈ¯ن»¥ç”±è؟™ن؛›هژںهگو¥ç؛؟و€§ه’Œï¼Œه†چهٹ ن¸ٹوœ€هگژçڑ„و®‹ه·®ه€¼و¥è،¨ç¤؛م€‚ه¾ˆوک¾ç„¶ï¼Œه¦‚وœو®‹ه·®ه€¼هœ¨هڈ¯ن»¥ه؟½ç•¥çڑ„范ه›´ه†…,هˆ™ن؟،هڈ·yه°±وک¯è؟™ن؛›هژںهگçڑ„ç؛؟و€§ç»„هگˆم€‚ه¦‚وœé€‰و‹©ن¸ژن؟،هڈ·yوœ€هŒ¹é…چçڑ„هژںهگï¼ںه¦‚ن½•و„ه»؛稀ç–ڈ逼è؟‘ه¹¶و±‚و®‹ه·®ï¼ںه¦‚ن½•è؟›è،Œè؟ن»£ï¼ںوˆ‘ن»¬و¥è¯¦ç»†ن»‹ç»چن½؟用MPè؟›è،Œن؟،هڈ·هˆ†è§£çڑ„و¥éھ¤ï¼ڑ[1] è®،ç®—ن؟،هڈ· y ن¸ژه—ه…¸çں©éکµن¸و¯ڈهˆ—(هژںهگ)çڑ„ه†…积,选و‹©ç»ه¯¹ه€¼وœ€ه¤§çڑ„ن¸€ن¸ھهژںهگ,ه®ƒه°±وک¯ن¸ژن؟،هڈ· y هœ¨وœ¬و¬،è؟ن»£è؟گç®—ن¸وœ€هŒ¹é…چçڑ„م€‚用ن¸“ن¸ڑوœ¯è¯و¥وڈڈè؟°ï¼ڑن»¤ن؟،هڈ·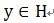 ,ن»ژه—ه…¸çں©éکµن¸é€‰و‹©ن¸€ن¸ھوœ€ن¸؛هŒ¹é…چçڑ„هژںهگ,و»،足
,ن»ژه—ه…¸çں©éکµن¸é€‰و‹©ن¸€ن¸ھوœ€ن¸؛هŒ¹é…چçڑ„هژںهگ,و»،足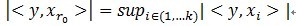 ,r0
è،¨ç¤؛ن¸€ن¸ھه—ه…¸çں©éکµçڑ„هˆ—ç´¢ه¼•م€‚è؟™و ·ï¼Œن؟،هڈ· y ه°±è¢«هˆ†è§£ن¸؛هœ¨وœ€هŒ¹é…چهژںهگ
,r0
è،¨ç¤؛ن¸€ن¸ھه—ه…¸çں©éکµçڑ„هˆ—ç´¢ه¼•م€‚è؟™و ·ï¼Œن؟،هڈ· y ه°±è¢«هˆ†è§£ن¸؛هœ¨وœ€هŒ¹é…چهژںهگ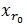 çڑ„ه‚ç›´وٹ•ه½±هˆ†é‡ڈه’Œو®‹ه€¼ن¸¤éƒ¨هˆ†ï¼Œهچ³ï¼ڑ
çڑ„ه‚ç›´وٹ•ه½±هˆ†é‡ڈه’Œو®‹ه€¼ن¸¤éƒ¨هˆ†ï¼Œهچ³ï¼ڑ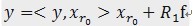 م€‚[2]ه¯¹و®‹ه€¼R1fè؟›è،Œو¥éھ¤[1]هگŒو ·çڑ„هˆ†è§£ï¼Œé‚£ن¹ˆç¬¬Kو¥هڈ¯ن»¥ه¾—هˆ°ï¼ڑ
م€‚[2]ه¯¹و®‹ه€¼R1fè؟›è،Œو¥éھ¤[1]هگŒو ·çڑ„هˆ†è§£ï¼Œé‚£ن¹ˆç¬¬Kو¥هڈ¯ن»¥ه¾—هˆ°ï¼ڑ
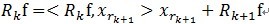 ,ه…¶ن¸
,ه…¶ن¸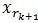 و»،足
و»،足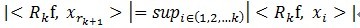 م€‚هڈ¯è§پ,ç»ڈè؟‡Kو¥هˆ†è§£هگژ,ن؟،هڈ· y 被هˆ†è§£ن¸؛ï¼ڑ
م€‚هڈ¯è§پ,ç»ڈè؟‡Kو¥هˆ†è§£هگژ,ن؟،هڈ· y 被هˆ†è§£ن¸؛ï¼ڑ ,ه…¶ن¸
,ه…¶ن¸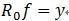 م€‚
م€‚
2.2 继ç»è®¨è®؛
(1)ن¸؛ن»€ن¹ˆè¦پهپ‡ه®ڑهœ¨Hilbertç©؛é—´ن¸ï¼ںHilbertç©؛é—´ه°±وک¯ه®ڑن¹‰ن؛†ه®Œه¤‡çڑ„ه†…积ç©؛م€‚ه¾ˆوک¾ç„¶ï¼ŒMPن¸çڑ„è®،ç®—ن½؟用هگ‘é‡ڈçڑ„ه†…积è؟گ算,و‰€ن»¥هœ¨هœ¨Hilbertç©؛é—´ن¸è؟›è،Œن؟،هڈ·هˆ†è§£çگ†و‰€ه½“然ن؛†م€‚ن»€ن¹ˆوک¯ه®Œه¤‡çڑ„ه†…积ç©؛é—´ï¼ں篇ه¹…وœ‰é™گه°±è¯·è‡ھه·±وگœç´¢ن¸€ن¸‹هگ§م€‚
(2)ن¸؛ن»€ن¹ˆهژںهگè¦پن؛‹ه…ˆè¢«ه½’ن¸€هŒ–ه¤„çگ†ن؛†ï¼Œهچ³ن¸ٹé¢çڑ„وڈڈè؟°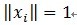 م€‚ه†…积ه¸¸ç”¨ن؛ژè®،ç®—ن¸€ن¸ھçں¢é‡ڈهœ¨ن¸€ن¸ھو–¹هگ‘ن¸ٹçڑ„وٹ•ه½±é•؟ه؛¦ï¼Œè؟™و—¶و–¹هگ‘çڑ„çں¢é‡ڈه؟…é،»وک¯هچ•ن½چçں¢é‡ڈم€‚MPن¸é€‰و‹©وœ€هŒ¹é…چçڑ„هژںهگوک¯ï¼Œوک¯é€‰و‹©ه†…积وœ€ه¤§çڑ„ن¸€ن¸ھ,ن¹ںه°±وک¯ن؟،هڈ·(وˆ–وک¯و®‹ه€¼)هœ¨هژںهگ(هچ•ن½چçڑ„)ه‚ç›´وٹ•ه½±é•؟ه؛¦وœ€é•؟çڑ„ن¸€ن¸ھ,و¯”ه¦‚第ن¸€و¬،هˆ†è§£è؟‡ç¨‹ن¸ï¼Œوٹ•ه½±é•؟ه؛¦ه°±وک¯
م€‚ه†…积ه¸¸ç”¨ن؛ژè®،ç®—ن¸€ن¸ھçں¢é‡ڈهœ¨ن¸€ن¸ھو–¹هگ‘ن¸ٹçڑ„وٹ•ه½±é•؟ه؛¦ï¼Œè؟™و—¶و–¹هگ‘çڑ„çں¢é‡ڈه؟…é،»وک¯هچ•ن½چçں¢é‡ڈم€‚MPن¸é€‰و‹©وœ€هŒ¹é…چçڑ„هژںهگوک¯ï¼Œوک¯é€‰و‹©ه†…积وœ€ه¤§çڑ„ن¸€ن¸ھ,ن¹ںه°±وک¯ن؟،هڈ·(وˆ–وک¯و®‹ه€¼)هœ¨هژںهگ(هچ•ن½چçڑ„)ه‚ç›´وٹ•ه½±é•؟ه؛¦وœ€é•؟çڑ„ن¸€ن¸ھ,و¯”ه¦‚第ن¸€و¬،هˆ†è§£è؟‡ç¨‹ن¸ï¼Œوٹ•ه½±é•؟ه؛¦ه°±وک¯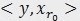 م€‚
م€‚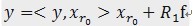 ,ن¸‰ن¸ھهگ‘é‡ڈ,و„وˆگن¸€ن¸ھن¸‰è§’ه½¢ï¼Œن¸”
,ن¸‰ن¸ھهگ‘é‡ڈ,و„وˆگن¸€ن¸ھن¸‰è§’ه½¢ï¼Œن¸”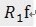 ه’Œ
ه’Œ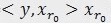 و£ن؛¤ï¼ˆن¸چ能说ه‚直,ن½†وک¯هڈ¯ن»¥وƒ³è±،ن؛Œç»´ç©؛é—´è؟™ن¸¤ن¸ھçں¢é‡ڈوک¯ه‚ç›´çڑ„)م€‚
و£ن؛¤ï¼ˆن¸چ能说ه‚直,ن½†وک¯هڈ¯ن»¥وƒ³è±،ن؛Œç»´ç©؛é—´è؟™ن¸¤ن¸ھçں¢é‡ڈوک¯ه‚ç›´çڑ„)م€‚
(3)MPç®—و³•وک¯و”¶و•›çڑ„,ه› ن¸؛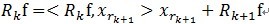 ,
,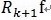 ه’Œ
ه’Œ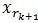 و£ن؛¤ï¼Œç”±è؟™ن¸¤ن¸ھهڈ¯ن»¥ه¾—ه‡؛
و£ن؛¤ï¼Œç”±è؟™ن¸¤ن¸ھهڈ¯ن»¥ه¾—ه‡؛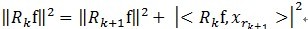 ,ه¾—ه‡؛و¯ڈن¸€ن¸ھو®‹ه€¼و¯”ن¸ٹن¸€و¬،çڑ„ه°ڈ,و•…而و”¶و•›م€‚
,ه¾—ه‡؛و¯ڈن¸€ن¸ھو®‹ه€¼و¯”ن¸ٹن¸€و¬،çڑ„ه°ڈ,و•…而و”¶و•›م€‚
2.3 MPç®—و³•çڑ„ç¼؛点
ه¦‚ن¸ٹو‰€è؟°ï¼Œه¦‚وœن؟،هڈ·(و®‹ه€¼)هœ¨ه·²é€‰و‹©çڑ„هژںهگè؟›è،Œه‚ç›´وٹ•ه½±وک¯éو£ن؛¤و€§çڑ„,è؟™ن¼ڑن½؟ه¾—و¯ڈو¬،è؟ن»£çڑ„结وœه¹¶ن¸چه°‘وœ€ن¼کçڑ„而وک¯و¬،وœ€ن¼کçڑ„,و”¶و•›éœ€è¦په¾ˆه¤ڑو¬،è؟ن»£م€‚ن¸¾ن¸ھن¾‹هگ说وکژن¸€ن¸‹ï¼ڑهœ¨ن؛Œç»´ç©؛é—´ن¸ٹ,وœ‰ن¸€ن¸ھن؟،هڈ· y 被 D=[x1, x2]و¥è،¨è¾¾ï¼ŒMPç®—و³•è؟ن»£ن¼ڑهڈ‘çژ°و€»وک¯هœ¨x1ه’Œx2ن¸ٹهڈچه¤چè؟ن»£ï¼Œهچ³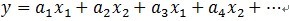 ,è؟™ن¸ھه°±وک¯ن؟،هڈ·(و®‹ه€¼)هœ¨ه·²é€‰و‹©çڑ„هژںهگè؟›è،Œه‚ç›´وٹ•ه½±çڑ„éو£ن؛¤و€§ه¯¼è‡´çڑ„م€‚ه†چ用ن¸¥è°¨çڑ„و–¹ه¼ڈوڈڈè؟°[1]هڈ¯èƒ½ه®¹وک“çگ†è§£:هœ¨Hilbertç©؛é—´Hن¸ï¼Œ
,è؟™ن¸ھه°±وک¯ن؟،هڈ·(و®‹ه€¼)هœ¨ه·²é€‰و‹©çڑ„هژںهگè؟›è،Œه‚ç›´وٹ•ه½±çڑ„éو£ن؛¤و€§ه¯¼è‡´çڑ„م€‚ه†چ用ن¸¥è°¨çڑ„و–¹ه¼ڈوڈڈè؟°[1]هڈ¯èƒ½ه®¹وک“çگ†è§£:هœ¨Hilbertç©؛é—´Hن¸ï¼Œ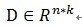 ,
,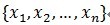 ,ه®ڑن¹‰
,ه®ڑن¹‰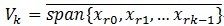 ,ه°±وک¯ه®ƒوک¯è؟™ن؛›هگ‘é‡ڈçڑ„ه¼ وˆگن¸çڑ„ن¸€ن¸ھ,MPو„é€ ن¸€ç§چè،¨è¾¾ه½¢ه¼ڈï¼ڑ
,ه°±وک¯ه®ƒوک¯è؟™ن؛›هگ‘é‡ڈçڑ„ه¼ وˆگن¸çڑ„ن¸€ن¸ھ,MPو„é€ ن¸€ç§چè،¨è¾¾ه½¢ه¼ڈï¼ڑ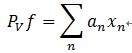 ;è؟™é‡Œçڑ„Pvfè،¨ç¤؛
fهœ¨Vن¸ٹçڑ„ن¸€ن¸ھو£ن؛¤وٹ•ه½±و“چن½œï¼Œé‚£ن¹ˆMPç®—و³•çڑ„第 k و¬،è؟ن»£çڑ„结وœهڈ¯ن»¥è،¨ç¤؛ه¦‚ن¸‹(ه‰چé¢وڈڈè؟°و—¶ن؟،هڈ·ن¸؛y,è؟™é‡Œهڈکوˆگfن؛†ï¼Œè¯·و³¨و„ڈ)ï¼ڑ
;è؟™é‡Œçڑ„Pvfè،¨ç¤؛
fهœ¨Vن¸ٹçڑ„ن¸€ن¸ھو£ن؛¤وٹ•ه½±و“چن½œï¼Œé‚£ن¹ˆMPç®—و³•çڑ„第 k و¬،è؟ن»£çڑ„结وœهڈ¯ن»¥è،¨ç¤؛ه¦‚ن¸‹(ه‰چé¢وڈڈè؟°و—¶ن؟،هڈ·ن¸؛y,è؟™é‡Œهڈکوˆگfن؛†ï¼Œè¯·و³¨و„ڈ)ï¼ڑ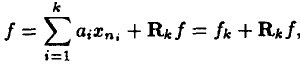
ه¦‚وœ  وک¯وœ€ن¼کçڑ„ké،¹è؟‘ن¼¼ه€¼ï¼Œه½“ن¸”ن»…ه½“
وک¯وœ€ن¼کçڑ„ké،¹è؟‘ن¼¼ه€¼ï¼Œه½“ن¸”ن»…ه½“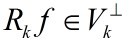 م€‚ç”±ن؛ژMPن»…能ن؟è¯پ
م€‚ç”±ن؛ژMPن»…能ن؟è¯پ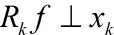 ,و‰€ن»¥
,و‰€ن»¥ ن¸€èˆ¬وƒ…ه†µن¸‹وک¯و¬،ن¼کçڑ„م€‚è؟™وک¯ن»€ن¹ˆو„ڈو€ه‘¢ï¼ں
ن¸€èˆ¬وƒ…ه†µن¸‹وک¯و¬،ن¼کçڑ„م€‚è؟™وک¯ن»€ن¹ˆو„ڈو€ه‘¢ï¼ں وک¯kن¸ھé،¹çڑ„ç؛؟و€§è،¨ç¤؛,è؟™ن¸ھ组هگˆçڑ„ه€¼ن½œن¸؛è؟‘ن¼¼ه€¼ï¼Œهڈھوœ‰هœ¨ç¬¬kن¸ھو®‹ه·®ه’Œ
وک¯kن¸ھé،¹çڑ„ç؛؟و€§è،¨ç¤؛,è؟™ن¸ھ组هگˆçڑ„ه€¼ن½œن¸؛è؟‘ن¼¼ه€¼ï¼Œهڈھوœ‰هœ¨ç¬¬kن¸ھو®‹ه·®ه’Œ و£ن؛¤ï¼Œو‰چوک¯وœ€ن¼کçڑ„م€‚ه¦‚وœç¬¬kن¸ھو®‹ه€¼ن¸ژ
و£ن؛¤ï¼Œو‰چوک¯وœ€ن¼کçڑ„م€‚ه¦‚وœç¬¬kن¸ھو®‹ه€¼ن¸ژ و£ن؛¤ï¼Œو„ڈه‘³è؟™ن¸ھو®‹ه€¼ن¸ژfkçڑ„ن»»و„ڈن¸€é،¹éƒ½ç؛؟و€§و— ه…³ï¼Œé‚£ن¹ˆç¬¬kن¸ھو®‹ه€¼هœ¨هگژé¢çڑ„هˆ†è§£è؟‡ç¨‹ن¸ï¼Œن¸چهڈ¯èƒ½ه‡؛çژ°fkن¸ه·²ç»ڈه‡؛çژ°çڑ„é،¹ï¼Œè؟™و‰چوک¯وœ€ن¼کçڑ„م€‚而ن¸€èˆ¬وƒ…ه†µن¸‹ï¼Œن¸چ能و»،足è؟™ن¸ھو،ن»¶ï¼ŒMPن¸€èˆ¬هڈھ能و»،足第kن¸ھو®‹ه·®ه’Œxkو£ن؛¤ï¼Œè؟™ن¹ںه°±وک¯ه‰چé¢ن¸؛ن»€ن¹ˆوڈگهˆ°â€œن؟،هڈ·(و®‹ه€¼)هœ¨ه·²é€‰و‹©çڑ„هژںهگè؟›è،Œه‚ç›´وٹ•ه½±وک¯éو£ن؛¤و€§çڑ„â€çڑ„هژںه› م€‚ه¦‚وœç¬¬kن¸ھو®‹ه·®ه’Œfkن¸چو£ن؛¤ï¼Œé‚£ن¹ˆهگژé¢çڑ„è؟ن»£è؟کن¼ڑه‡؛çژ°fkن¸ه·²ç»ڈه‡؛çژ°çڑ„é،¹ï¼Œه¾ˆوک¾ç„¶fkه°±ن¸چوک¯وœ€ن¼کçڑ„,è؟™ن¹ںه°±وک¯ن¸؛ن»€ن¹ˆè¯´MPو”¶و•›ه°±éœ€è¦پو›´ه¤ڑو¬،è؟ن»£çڑ„هژںه› م€‚ن¸چوک¯è¯´MPن¸€ه®ڑه¾—هˆ°ن¸چهˆ°وœ€ن¼ک解,而ن¸”ه…¶ه‰چé¢وڈڈè؟°çڑ„特و€§ه¯¼è‡´ن¸€èˆ¬ه¾—هˆ°ن¸چهˆ°وœ€ن¼ک解而وک¯و¬،ن¼ک解م€‚é‚£ن¹ˆï¼Œوœ‰و²،وœ‰هٹو³•è®©ç¬¬kن¸ھو®‹ه·®ن¸ژ
و£ن؛¤ï¼Œو„ڈه‘³è؟™ن¸ھو®‹ه€¼ن¸ژfkçڑ„ن»»و„ڈن¸€é،¹éƒ½ç؛؟و€§و— ه…³ï¼Œé‚£ن¹ˆç¬¬kن¸ھو®‹ه€¼هœ¨هگژé¢çڑ„هˆ†è§£è؟‡ç¨‹ن¸ï¼Œن¸چهڈ¯èƒ½ه‡؛çژ°fkن¸ه·²ç»ڈه‡؛çژ°çڑ„é،¹ï¼Œè؟™و‰چوک¯وœ€ن¼کçڑ„م€‚而ن¸€èˆ¬وƒ…ه†µن¸‹ï¼Œن¸چ能و»،足è؟™ن¸ھو،ن»¶ï¼ŒMPن¸€èˆ¬هڈھ能و»،足第kن¸ھو®‹ه·®ه’Œxkو£ن؛¤ï¼Œè؟™ن¹ںه°±وک¯ه‰چé¢ن¸؛ن»€ن¹ˆوڈگهˆ°â€œن؟،هڈ·(و®‹ه€¼)هœ¨ه·²é€‰و‹©çڑ„هژںهگè؟›è،Œه‚ç›´وٹ•ه½±وک¯éو£ن؛¤و€§çڑ„â€çڑ„هژںه› م€‚ه¦‚وœç¬¬kن¸ھو®‹ه·®ه’Œfkن¸چو£ن؛¤ï¼Œé‚£ن¹ˆهگژé¢çڑ„è؟ن»£è؟کن¼ڑه‡؛çژ°fkن¸ه·²ç»ڈه‡؛çژ°çڑ„é،¹ï¼Œه¾ˆوک¾ç„¶fkه°±ن¸چوک¯وœ€ن¼کçڑ„,è؟™ن¹ںه°±وک¯ن¸؛ن»€ن¹ˆè¯´MPو”¶و•›ه°±éœ€è¦پو›´ه¤ڑو¬،è؟ن»£çڑ„هژںه› م€‚ن¸چوک¯è¯´MPن¸€ه®ڑه¾—هˆ°ن¸چهˆ°وœ€ن¼ک解,而ن¸”ه…¶ه‰چé¢وڈڈè؟°çڑ„特و€§ه¯¼è‡´ن¸€èˆ¬ه¾—هˆ°ن¸چهˆ°وœ€ن¼ک解而وک¯و¬،ن¼ک解م€‚é‚£ن¹ˆï¼Œوœ‰و²،وœ‰هٹو³•è®©ç¬¬kن¸ھو®‹ه·®ن¸ژ و£ن؛¤ï¼Œو–¹و³•وک¯وœ‰çڑ„,è؟™ه°±وک¯ن¸‹é¢è¦پè°ˆهˆ°çڑ„OMPç®—و³•م€‚
و£ن؛¤ï¼Œو–¹و³•وک¯وœ‰çڑ„,è؟™ه°±وک¯ن¸‹é¢è¦پè°ˆهˆ°çڑ„OMPç®—و³•م€‚
3.OMPç®—و³•
3.1 ç®—و³•وڈڈè؟°
OMPç®—و³•çڑ„و”¹è؟›ن¹‹ه¤„هœ¨ن؛ژï¼ڑهœ¨هˆ†è§£çڑ„و¯ڈن¸€و¥ه¯¹و‰€é€‰و‹©çڑ„ه…¨éƒ¨هژںهگè؟›è،Œو£ن؛¤هŒ–ه¤„çگ†ï¼Œè؟™ن½؟ه¾—هœ¨ç²¾ه؛¦è¦پو±‚相هگŒçڑ„وƒ…ه†µن¸‹ï¼ŒOMPç®—و³•çڑ„و”¶و•›é€ںه؛¦و›´ه؟«م€‚
é‚£ن¹ˆهœ¨و¯ڈن¸€و¥ن¸ه¦‚ن½•ه¯¹و‰€é€‰و‹©çڑ„ه…¨éƒ¨هژںهگè؟›è،Œو£ن؛¤هŒ–ه¤„çگ†ه‘¢ï¼ںهœ¨و£ه¼ڈوڈڈè؟°OMPç®—و³•ه‰چ,ه…ˆçœ‹ن¸€ç‚¹هں؛ç،€و€وƒ³م€‚
ه…ˆçœ‹ن¸€ن¸ھ k éک¶و¨،ه‹ï¼Œè،¨ç¤؛ن؟،هڈ· f ç»ڈè؟‡ k و¥هˆ†è§£هگژçڑ„وƒ…ه†µï¼Œن¼¼ن¹ژه¾ˆçœ¼ç†ں,ن½†è¦پو³¨و„ڈه®ƒن¸ژMPç®—و³•ن¸چهگŒن¹‹ه¤„,ه®ƒçڑ„و®‹ه€¼ن¸ژه‰چé¢و¯ڈن¸ھهˆ†é‡ڈو£ن؛¤ï¼Œè؟™ه°±وک¯ن¸؛ن»€ن¹ˆè؟™ن¸ھç®—و³•ه¤ڑن؛†ن¸€ن¸ھو£ن؛¤çڑ„هژںه› ,MPن¸ن»…ن¸ژوœ€è؟‘选ه‡؛çڑ„çڑ„é‚£ن¸€é،¹و£ن؛¤م€‚
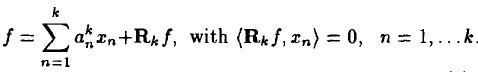 (1)
(1)
k + 1 éک¶و¨،ه‹ه¦‚ن¸‹ï¼ڑ
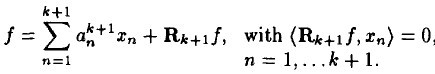 (2)
(2)
ه؛”用 k + 1éک¶و¨،ه‹ه‡ڈهژ»k éک¶و¨،ه‹ï¼Œه¾—هˆ°ه¦‚ن¸‹ï¼ڑ
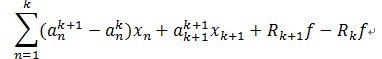 (3)
(3)
وˆ‘ن»¬çں¥éپ“,ه—ه…¸çں©éکµDçڑ„هژںهگوک¯éو£ن؛¤çڑ„,ه¼•ه…¥ن¸€ن¸ھè¾…هٹ©و¨،ه‹ï¼Œه®ƒوک¯è،¨ç¤؛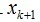 ه¯¹ه‰چkن¸ھé،¹
ه¯¹ه‰چkن¸ھé،¹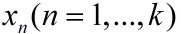 çڑ„ن¾èµ–,وڈڈè؟°ه¦‚ن¸‹ï¼ڑ
çڑ„ن¾èµ–,وڈڈè؟°ه¦‚ن¸‹ï¼ڑ
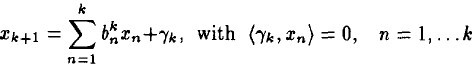 (4)
(4)
ه’Œه‰چé¢وڈڈè؟°ç±»ن¼¼ï¼Œ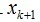 هœ¨span(x1, ...xk)ن¹‹ن¸€ن¸ٹçڑ„و£ن؛¤وٹ•ه½±و“چن½œï¼Œهگژé¢çڑ„é،¹وک¯و®‹ه€¼م€‚è؟™ن¸ھه…³ç³»ç”¨و•°ه¦ç¬¦هڈ·وڈڈè؟°ï¼ڑ
هœ¨span(x1, ...xk)ن¹‹ن¸€ن¸ٹçڑ„و£ن؛¤وٹ•ه½±و“چن½œï¼Œهگژé¢çڑ„é،¹وک¯و®‹ه€¼م€‚è؟™ن¸ھه…³ç³»ç”¨و•°ه¦ç¬¦هڈ·وڈڈè؟°ï¼ڑ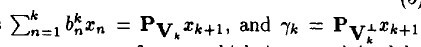
请و³¨و„ڈ,è؟™é‡Œçڑ„ a ه’Œ b çڑ„ن¸ٹو ‡è،¨ç¤؛第 k و¥و—¶çڑ„هڈ–ه€¼م€‚
ه°†(4)ه¸¦ه…¥(3)ن¸ï¼Œوœ‰ï¼ڑ
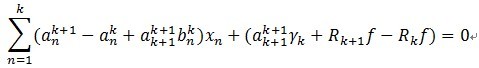 (5)
(5)
ه¦‚وœن¸€ن¸‹ن¸¤ن¸ھه¼ڈهگوˆگ立,(5)ه؟…然وˆگç«‹م€‚
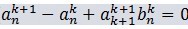 (6)
(6)
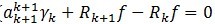 (7)
(7)
ن»¤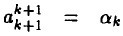 ,وœ‰
,وœ‰
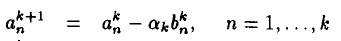
ه…¶ن¸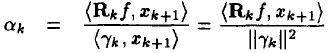 م€‚
م€‚
akçڑ„ه€¼وک¯ç”±و±‚و³•ه¾ˆç®€هچ•ï¼Œé€ڑè؟‡ه¯¹(7)ه·¦هڈ³ن¸¤è¾¹و·»هٹ 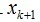 ن½œه†…积و¶ˆه‡ڈه¾—هˆ°ï¼ڑ
ن½œه†…积و¶ˆه‡ڈه¾—هˆ°ï¼ڑ
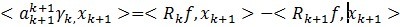
هگژè¾¹çڑ„第ن؛Œé،¹ه› ن¸؛ه®ƒن»¬و£ن؛¤ï¼Œو‰€ن»¥ن¸؛0,و‰€ن»¥هڈ¯ن»¥ه¾—ه‡؛akçڑ„第ن¸€éƒ¨هˆ†م€‚ه¯¹ن؛ژ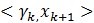 ,هœ¨ï¼ˆ4)ه·¦هڈ³ن¸¤è¾¹ن¸ن¸ژ
,هœ¨ï¼ˆ4)ه·¦هڈ³ن¸¤è¾¹ن¸ن¸ژ ن½œه†…积,هڈ¯ن»¥ه¾—هˆ°akçڑ„第ن؛Œéƒ¨هˆ†م€‚
ن½œه†…积,هڈ¯ن»¥ه¾—هˆ°akçڑ„第ن؛Œéƒ¨هˆ†م€‚
ه¯¹ن؛ژ(4),هڈ¯ن»¥و±‚ه‡؛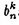 ,و±‚çڑ„و¥éھ¤è¯·هڈ‚è§پهڈ‚考و–‡ن»¶çڑ„è®،算细èٹ‚部هˆ†م€‚ن¸؛ن»€ن¹ˆè؟™é‡Œن¸چوڈگ,ه› ن¸؛هگژé¢ن¼ڑن»‹ç»چو›´ç®€هچ•çڑ„و–¹و³•و¥è®،ç®—م€‚
,و±‚çڑ„و¥éھ¤è¯·هڈ‚è§پهڈ‚考و–‡ن»¶çڑ„è®،算细èٹ‚部هˆ†م€‚ن¸؛ن»€ن¹ˆè؟™é‡Œن¸چوڈگ,ه› ن¸؛هگژé¢ن¼ڑن»‹ç»چو›´ç®€هچ•çڑ„و–¹و³•و¥è®،ç®—م€‚
3.2 و”¶و•›و€§è¯پوکژ
é€ڑè؟‡(7)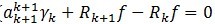 ,由ن؛ژ
,由ن؛ژ ن¸ژ
ن¸ژ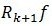 و£ن؛¤ï¼Œه°†ن¸¤ن¸ھو®‹ه€¼ç§»هˆ°هڈ³è¾¹هگژو±‚ن؛ŒèŒƒçڑ„ه¹³و–¹ï¼Œه¹¶ه°†akçڑ„ه€¼ن»£ه…¥هڈ¯ن»¥ه¾—هˆ°ï¼ڑ
و£ن؛¤ï¼Œه°†ن¸¤ن¸ھو®‹ه€¼ç§»هˆ°هڈ³è¾¹هگژو±‚ن؛ŒèŒƒçڑ„ه¹³و–¹ï¼Œه¹¶ه°†akçڑ„ه€¼ن»£ه…¥هڈ¯ن»¥ه¾—هˆ°ï¼ڑ
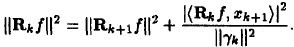
هڈ¯è§پو¯ڈن¸€و¬،و®‹ه·®و¯”ن¸ٹن¸€و¬،و®‹ه·®ه°ڈ,هڈ¯è§پوک¯و”¶و•›çڑ„م€‚
3.3 ç®—و³•و¥éھ¤
و•´ن¸ھOMPç®—و³•çڑ„و¥éھ¤ه¦‚ن¸‹ï¼ڑ

ç”±ن؛ژوœ‰ن؛†ن¸ٹé¢çڑ„و¥é¾™هژ»è„‰ï¼Œè؟™ن¸ھç®—و³•ه°±ç›¸ه½“ه¥½çگ†è§£ن؛†م€‚
هˆ°è؟™é‡Œè؟کن¸چç®—ه®Œï¼Œهگژو¥OMPçڑ„è؟ن»£è؟گ算用هڈ¦ه¤–ن¸€ç§چو–¹و³•هڈ¯ن»¥è®،ç®—ه¾—çں¥ï¼Œوœ‰ن½چهگŒه¦çڑ„è®؛و–‡[2]وڈڈè؟°ه°±éه¸¸ه¥½ï¼Œوˆ‘ه°±ç›´وژ¥ه¼•ç”¨è؟›و¥ï¼ڑ


ه¯¹و¯”ن¸è‹±و–‡وڈڈè؟°ï¼Œوœ¬è´¨éƒ½وک¯ن¸€و ·ï¼Œهڈھوک¯وœ‰ç»†ه¾®çڑ„ه·®هˆ«م€‚è؟™é‡Œé،؛ن¾؟è´´ه‡؛网ن¸€ه“¥ن»¬ه†™çڑ„OMPç®—و³•çڑ„ن»£ç پ,و؛گه‡؛ه¤„ن¸چه¾—而çں¥ï¼Œه…±ن؛«ç»™ه¤§ه®¶م€‚

ه†چè´´هڈ¦ه¤–ن¸€ن¸ھو´‹ç‰›paper[3]ن¸ه…³ن؛ژOMPçڑ„وڈڈè؟°ï¼Œن¹‹و‰€ن»¥ه¼•ه…¥ï¼Œوک¯ه› ن¸؛ه®ƒوڈڈè؟°çڑ„éه¸¸ن¸¥è°¨ï¼Œن½†وک¯ن¹ںوœ‰ç‚¹è‹¦و¶©éڑ¾و‡‚,ن¸چè؟‡وœ‰ن؛†ن¸ٹé¢çڑ„هں؛ç،€ï¼Œه°±ه®¹وک“ه¤ڑن؛†م€‚

ه®ƒçڑ„وڈڈè؟°ن¸çڑ„Sweepو¥éھ¤ه°±وک¯ه¯»و‰¾ن¸ژه½“ه‰چو®‹ه·®وœ€ه¤§çڑ„ه†…积و—¶هˆ—هœ¨ه—ه…¸çں©éکµDن¸çڑ„ç´¢ه¼•ï¼Œه®ƒçڑ„è؟™ن¸ھو¥éھ¤وڈڈè؟°è¯´وکژن¸؛ن»€ن¹ˆè¦پ选و‹©ه†…积وœ€ه¤§çڑ„ن»¥هڈٹه¦‚ن½•é€‰و‹©م€‚è§پن¸‹ه›¾ï¼Œè¯´çڑ„éه¸¸و¸…و™°م€‚
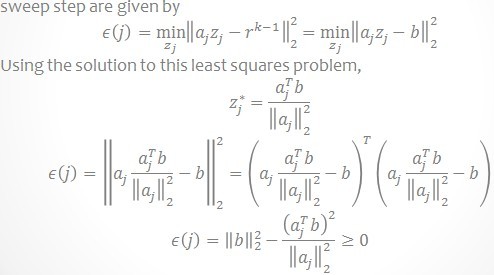
ه®ƒçڑ„ç®—و³•و¥éھ¤Update Provisional Solutionن¸و±‚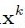 ه¾ˆç®€هچ•ï¼Œه°±وک¯هœ¨ b = Ax ه·²çں¥ Aه’Œbو±‚x, هœ¨xçڑ„وœ€ه°ڈن؛ŒèŒƒه°±وک¯Açڑ„ن¼ھ逆ن¸ژb相ن¹ک,هچ³ï¼ڑ
ه¾ˆç®€هچ•ï¼Œه°±وک¯هœ¨ b = Ax ه·²çں¥ Aه’Œbو±‚x, هœ¨xçڑ„وœ€ه°ڈن؛ŒèŒƒه°±وک¯Açڑ„ن¼ھ逆ن¸ژb相ن¹ک,هچ³ï¼ڑ
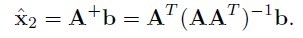
看ن¸ٹهژ»ه¤´ç–¼ï¼Œه…¶ه®ç”¨matlabéه¸¸ç®€هچ•ï¼Œçœ‹çœ‹ن¸ٹé¢çڑ„matlabçڑ„ن»£ç په°±وکژ白ن؛†م€‚
وˆ‘ن»¬هڈ¯ن»¥çœ‹ه¾—ه‡؛و¥ï¼Œç®—و³•وµپ程و¸…و™°وکژن؛†ï¼Œè؟کوک¯ه¾ˆه¥½çگ†è§£çڑ„م€‚è؟™و£وک¯OMPç®—و³•çڑ„é…هٹ›ï¼Œن½œن¸؛ه·¥ه…·ن½؟用简هچ•ï¼ŒèƒŒهگژهچ´éڑگè—ڈç€ه¾ˆوœ‰è¶£çڑ„و€وƒ³م€‚
ه†™è؟™ç¯‡هچڑه®¢çڑ„ç›®çڑ„,وک¯ه› ن¸؛وگœç´¢ن؛†ن¸€ن¸‹ï¼ŒMPه’ŒOMPو²،وœ‰ن؛؛ه¾ˆè¯¦ç»†çڑ„ن»‹ç»چم€‚و–‡çŒ®[1]讲çڑ„ه¾ˆو¸…و¥ڑçڑ„,ه¤§ه®¶وœ‰ه…´è¶£هڈ¯ن»¥و‰¾و¥çœ‹çœ‹م€‚ن¸چè¦پ被è€پو؟هڈ‘çژ°وˆ‘ه±…然هœ¨وگœن¸و–‡و–‡çŒ®è؟که†™ن¸و–‡هچڑه®¢م€‚
هڈ‚考و–‡çŒ®ï¼ڑ
[1]Orthogonal Matching Pursuit:Recursive Function Approximat ion with Applications to Wavelet Decomposition
[2]http://wenku.baidu.com/view/22f3171614791711cc7917e4.html
[3]From Sparse Solutions of Systems of Equations to Sparse Modeling of Signals and Images
هˆ†ن؛«هˆ°ï¼ڑ





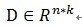 ,ه…¶ن¸ه®ƒçڑ„و¯ڈهˆ—è،¨ç¤؛ن¸€ç§چهژںه‹ن؟،هڈ·çڑ„هژںهگم€‚ç»™ه®ڑن¸€ن¸ھن؟،هڈ·y,ه®ƒهڈ¯ن»¥è¢«è،¨ç¤؛وˆگè؟™ن؛›هژںهگçڑ„稀ç–ڈç؛؟و€§ç»„هگˆم€‚ن؟،هڈ· y هڈ¯ن»¥è¢«è،¨è¾¾ن¸؛ y = Dx ,وˆ–者
,ه…¶ن¸ه®ƒçڑ„و¯ڈهˆ—è،¨ç¤؛ن¸€ç§چهژںه‹ن؟،هڈ·çڑ„هژںهگم€‚ç»™ه®ڑن¸€ن¸ھن؟،هڈ·y,ه®ƒهڈ¯ن»¥è¢«è،¨ç¤؛وˆگè؟™ن؛›هژںهگçڑ„稀ç–ڈç؛؟و€§ç»„هگˆم€‚ن؟،هڈ· y هڈ¯ن»¥è¢«è،¨è¾¾ن¸؛ y = Dx ,وˆ–者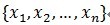 و„وˆگه—ه…¸çں©éکµD,ه…¶ن¸و¯ڈن¸ھهگ‘é‡ڈهڈ¯ن»¥ç§°ن¸؛هژںهگ(atom),ه…¶é•؟ه؛¦ن¸ژ被è،¨ç¤؛ن؟،هڈ· y çڑ„é•؟ه؛¦n相هگŒï¼Œè€Œن¸”è؟™ن؛›هگ‘é‡ڈه·²ن½œن¸؛ه½’ن¸€هŒ–ه¤„çگ†ï¼Œهچ³|
و„وˆگه—ه…¸çں©éکµD,ه…¶ن¸و¯ڈن¸ھهگ‘é‡ڈهڈ¯ن»¥ç§°ن¸؛هژںهگ(atom),ه…¶é•؟ه؛¦ن¸ژ被è،¨ç¤؛ن؟،هڈ· y çڑ„é•؟ه؛¦n相هگŒï¼Œè€Œن¸”è؟™ن؛›هگ‘é‡ڈه·²ن½œن¸؛ه½’ن¸€هŒ–ه¤„çگ†ï¼Œهچ³|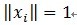 ,ن¹ںه°±وک¯هچ•ن½چهگ‘é‡ڈé•؟ه؛¦ن¸؛1م€‚MPç®—و³•çڑ„هں؛وœ¬و€وƒ³ï¼ڑن»ژه—ه…¸çں©éکµD(ن¹ں称ن¸؛è؟‡ه®Œه¤‡هژںهگه؛“ن¸ï¼‰ï¼Œé€‰و‹©ن¸€ن¸ھن¸ژن؟،هڈ·
y وœ€هŒ¹é…چçڑ„هژںهگ(ن¹ںه°±وک¯وںگهˆ—),و„ه»؛ن¸€ن¸ھ稀ç–ڈ逼è؟‘,ه¹¶و±‚ه‡؛ن؟،هڈ·و®‹ه·®ï¼Œç„¶هگژ继ç»é€‰و‹©ن¸ژن؟،هڈ·و®‹ه·®وœ€هŒ¹é…چçڑ„هژںهگ,هڈچه¤چè؟ن»£ï¼Œن؟،هڈ·yهڈ¯ن»¥ç”±è؟™ن؛›هژںهگو¥ç؛؟و€§ه’Œï¼Œه†چهٹ ن¸ٹوœ€هگژçڑ„و®‹ه·®ه€¼و¥è،¨ç¤؛م€‚ه¾ˆوک¾ç„¶ï¼Œه¦‚وœو®‹ه·®ه€¼هœ¨هڈ¯ن»¥ه؟½ç•¥çڑ„范ه›´ه†…,هˆ™ن؟،هڈ·yه°±وک¯è؟™ن؛›هژںهگçڑ„ç؛؟و€§ç»„هگˆم€‚ه¦‚وœé€‰و‹©ن¸ژن؟،هڈ·yوœ€هŒ¹é…چçڑ„هژںهگï¼ںه¦‚ن½•و„ه»؛稀ç–ڈ逼è؟‘ه¹¶و±‚و®‹ه·®ï¼ںه¦‚ن½•è؟›è،Œè؟ن»£ï¼ںوˆ‘ن»¬و¥è¯¦ç»†ن»‹ç»چن½؟用MPè؟›è،Œن؟،هڈ·هˆ†è§£çڑ„و¥éھ¤ï¼ڑ[1] è®،ç®—ن؟،هڈ· y ن¸ژه—ه…¸çں©éکµن¸و¯ڈهˆ—(هژںهگ)çڑ„ه†…积,选و‹©ç»ه¯¹ه€¼وœ€ه¤§çڑ„ن¸€ن¸ھهژںهگ,ه®ƒه°±وک¯ن¸ژن؟،هڈ· y هœ¨وœ¬و¬،è؟ن»£è؟گç®—ن¸وœ€هŒ¹é…چçڑ„م€‚用ن¸“ن¸ڑوœ¯è¯و¥وڈڈè؟°ï¼ڑن»¤ن؟،هڈ·
,ن¹ںه°±وک¯هچ•ن½چهگ‘é‡ڈé•؟ه؛¦ن¸؛1م€‚MPç®—و³•çڑ„هں؛وœ¬و€وƒ³ï¼ڑن»ژه—ه…¸çں©éکµD(ن¹ں称ن¸؛è؟‡ه®Œه¤‡هژںهگه؛“ن¸ï¼‰ï¼Œé€‰و‹©ن¸€ن¸ھن¸ژن؟،هڈ·
y وœ€هŒ¹é…چçڑ„هژںهگ(ن¹ںه°±وک¯وںگهˆ—),و„ه»؛ن¸€ن¸ھ稀ç–ڈ逼è؟‘,ه¹¶و±‚ه‡؛ن؟،هڈ·و®‹ه·®ï¼Œç„¶هگژ继ç»é€‰و‹©ن¸ژن؟،هڈ·و®‹ه·®وœ€هŒ¹é…چçڑ„هژںهگ,هڈچه¤چè؟ن»£ï¼Œن؟،هڈ·yهڈ¯ن»¥ç”±è؟™ن؛›هژںهگو¥ç؛؟و€§ه’Œï¼Œه†چهٹ ن¸ٹوœ€هگژçڑ„و®‹ه·®ه€¼و¥è،¨ç¤؛م€‚ه¾ˆوک¾ç„¶ï¼Œه¦‚وœو®‹ه·®ه€¼هœ¨هڈ¯ن»¥ه؟½ç•¥çڑ„范ه›´ه†…,هˆ™ن؟،هڈ·yه°±وک¯è؟™ن؛›هژںهگçڑ„ç؛؟و€§ç»„هگˆم€‚ه¦‚وœé€‰و‹©ن¸ژن؟،هڈ·yوœ€هŒ¹é…چçڑ„هژںهگï¼ںه¦‚ن½•و„ه»؛稀ç–ڈ逼è؟‘ه¹¶و±‚و®‹ه·®ï¼ںه¦‚ن½•è؟›è،Œè؟ن»£ï¼ںوˆ‘ن»¬و¥è¯¦ç»†ن»‹ç»چن½؟用MPè؟›è،Œن؟،هڈ·هˆ†è§£çڑ„و¥éھ¤ï¼ڑ[1] è®،ç®—ن؟،هڈ· y ن¸ژه—ه…¸çں©éکµن¸و¯ڈهˆ—(هژںهگ)çڑ„ه†…积,选و‹©ç»ه¯¹ه€¼وœ€ه¤§çڑ„ن¸€ن¸ھهژںهگ,ه®ƒه°±وک¯ن¸ژن؟،هڈ· y هœ¨وœ¬و¬،è؟ن»£è؟گç®—ن¸وœ€هŒ¹é…چçڑ„م€‚用ن¸“ن¸ڑوœ¯è¯و¥وڈڈè؟°ï¼ڑن»¤ن؟،هڈ·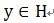 ,ن»ژه—ه…¸çں©éکµن¸é€‰و‹©ن¸€ن¸ھوœ€ن¸؛هŒ¹é…چçڑ„هژںهگ,و»،足
,ن»ژه—ه…¸çں©éکµن¸é€‰و‹©ن¸€ن¸ھوœ€ن¸؛هŒ¹é…چçڑ„هژںهگ,و»،足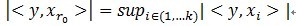 ,r0
è،¨ç¤؛ن¸€ن¸ھه—ه…¸çں©éکµçڑ„هˆ—ç´¢ه¼•م€‚è؟™و ·ï¼Œن؟،هڈ· y ه°±è¢«هˆ†è§£ن¸؛هœ¨وœ€هŒ¹é…چهژںهگ
,r0
è،¨ç¤؛ن¸€ن¸ھه—ه…¸çں©éکµçڑ„هˆ—ç´¢ه¼•م€‚è؟™و ·ï¼Œن؟،هڈ· y ه°±è¢«هˆ†è§£ن¸؛هœ¨وœ€هŒ¹é…چهژںهگ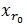 çڑ„ه‚ç›´وٹ•ه½±هˆ†é‡ڈه’Œو®‹ه€¼ن¸¤éƒ¨هˆ†ï¼Œهچ³ï¼ڑ
çڑ„ه‚ç›´وٹ•ه½±هˆ†é‡ڈه’Œو®‹ه€¼ن¸¤éƒ¨هˆ†ï¼Œهچ³ï¼ڑ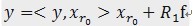 م€‚[2]ه¯¹و®‹ه€¼R1fè؟›è،Œو¥éھ¤[1]هگŒو ·çڑ„هˆ†è§£ï¼Œé‚£ن¹ˆç¬¬Kو¥هڈ¯ن»¥ه¾—هˆ°ï¼ڑ
م€‚[2]ه¯¹و®‹ه€¼R1fè؟›è،Œو¥éھ¤[1]هگŒو ·çڑ„هˆ†è§£ï¼Œé‚£ن¹ˆç¬¬Kو¥هڈ¯ن»¥ه¾—هˆ°ï¼ڑ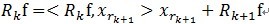 ,ه…¶ن¸
,ه…¶ن¸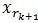 و»،足
و»،足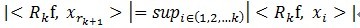 م€‚هڈ¯è§پ,ç»ڈè؟‡Kو¥هˆ†è§£هگژ,ن؟،هڈ· y 被هˆ†è§£ن¸؛ï¼ڑ
م€‚هڈ¯è§پ,ç»ڈè؟‡Kو¥هˆ†è§£هگژ,ن؟،هڈ· y 被هˆ†è§£ن¸؛ï¼ڑ ,ه…¶ن¸
,ه…¶ن¸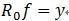 م€‚
م€‚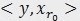 م€‚
م€‚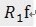 ه’Œ
ه’Œ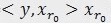 و£ن؛¤ï¼ˆن¸چ能说ه‚直,ن½†وک¯هڈ¯ن»¥وƒ³è±،ن؛Œç»´ç©؛é—´è؟™ن¸¤ن¸ھçں¢é‡ڈوک¯ه‚ç›´çڑ„)م€‚
و£ن؛¤ï¼ˆن¸چ能说ه‚直,ن½†وک¯هڈ¯ن»¥وƒ³è±،ن؛Œç»´ç©؛é—´è؟™ن¸¤ن¸ھçں¢é‡ڈوک¯ه‚ç›´çڑ„)م€‚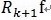 ه’Œ
ه’Œ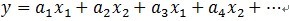 ,è؟™ن¸ھه°±وک¯ن؟،هڈ·(و®‹ه€¼)هœ¨ه·²é€‰و‹©çڑ„هژںهگè؟›è،Œه‚ç›´وٹ•ه½±çڑ„éو£ن؛¤و€§ه¯¼è‡´çڑ„م€‚ه†چ用ن¸¥è°¨çڑ„و–¹ه¼ڈوڈڈè؟°[1]هڈ¯èƒ½ه®¹وک“çگ†è§£:هœ¨Hilbertç©؛é—´Hن¸ï¼Œ
,è؟™ن¸ھه°±وک¯ن؟،هڈ·(و®‹ه€¼)هœ¨ه·²é€‰و‹©çڑ„هژںهگè؟›è،Œه‚ç›´وٹ•ه½±çڑ„éو£ن؛¤و€§ه¯¼è‡´çڑ„م€‚ه†چ用ن¸¥è°¨çڑ„و–¹ه¼ڈوڈڈè؟°[1]هڈ¯èƒ½ه®¹وک“çگ†è§£:هœ¨Hilbertç©؛é—´Hن¸ï¼Œ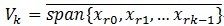 ,ه°±وک¯ه®ƒوک¯è؟™ن؛›هگ‘é‡ڈçڑ„ه¼ وˆگن¸çڑ„ن¸€ن¸ھ,MPو„é€ ن¸€ç§چè،¨è¾¾ه½¢ه¼ڈï¼ڑ
,ه°±وک¯ه®ƒوک¯è؟™ن؛›هگ‘é‡ڈçڑ„ه¼ وˆگن¸çڑ„ن¸€ن¸ھ,MPو„é€ ن¸€ç§چè،¨è¾¾ه½¢ه¼ڈï¼ڑ وک¯وœ€ن¼کçڑ„ké،¹è؟‘ن¼¼ه€¼ï¼Œه½“ن¸”ن»…ه½“
وک¯وœ€ن¼کçڑ„ké،¹è؟‘ن¼¼ه€¼ï¼Œه½“ن¸”ن»…ه½“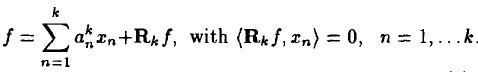 (1)
(1)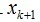 ه¯¹ه‰چkن¸ھé،¹
ه¯¹ه‰چkن¸ھé،¹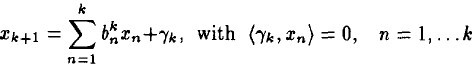 (4)
(4)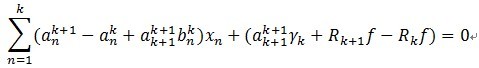 (5)
(5)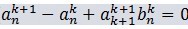 (6)
(6)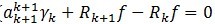 (7)
(7) ن½œه†…积,هڈ¯ن»¥ه¾—هˆ°akçڑ„第ن؛Œéƒ¨هˆ†م€‚
ن½œه†…积,هڈ¯ن»¥ه¾—هˆ°akçڑ„第ن؛Œéƒ¨هˆ†م€‚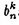 ,و±‚çڑ„و¥éھ¤è¯·هڈ‚è§پهڈ‚考و–‡ن»¶çڑ„è®،算细èٹ‚部هˆ†م€‚ن¸؛ن»€ن¹ˆè؟™é‡Œن¸چوڈگ,ه› ن¸؛هگژé¢ن¼ڑن»‹ç»چو›´ç®€هچ•çڑ„و–¹و³•و¥è®،ç®—م€‚
,و±‚çڑ„و¥éھ¤è¯·هڈ‚è§پهڈ‚考و–‡ن»¶çڑ„è®،算细èٹ‚部هˆ†م€‚ن¸؛ن»€ن¹ˆè؟™é‡Œن¸چوڈگ,ه› ن¸؛هگژé¢ن¼ڑن»‹ç»چو›´ç®€هچ•çڑ„و–¹و³•و¥è®،ç®—م€‚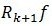 و£ن؛¤ï¼Œه°†ن¸¤ن¸ھو®‹ه€¼ç§»هˆ°هڈ³è¾¹هگژو±‚ن؛ŒèŒƒçڑ„ه¹³و–¹ï¼Œه¹¶ه°†akçڑ„ه€¼ن»£ه…¥هڈ¯ن»¥ه¾—هˆ°ï¼ڑ
و£ن؛¤ï¼Œه°†ن¸¤ن¸ھو®‹ه€¼ç§»هˆ°هڈ³è¾¹هگژو±‚ن؛ŒèŒƒçڑ„ه¹³و–¹ï¼Œه¹¶ه°†akçڑ„ه€¼ن»£ه…¥هڈ¯ن»¥ه¾—هˆ°ï¼ڑ




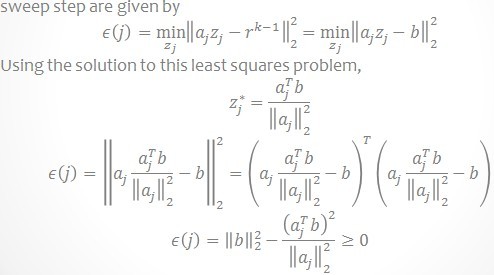



相ه…³وژ¨èچگ
هœ¨ن؟،هڈ·ه¤„çگ†ه’Œوœ؛ه™¨ه¦ن¹ 领هںں,稀ç–ڈè،¨ç¤؛çگ†è®؛ه·²ç»ڈوˆگن¸؛ن¸€ن¸ھé‡چè¦پçڑ„ç ”ç©¶و–¹هگ‘م€‚..."MPç®—و³•"ه’Œ"OMPç®—و³•"ن¸¤ن¸ھو–‡ن»¶هڈ¯èƒ½هŒ…هگ«ن؛†è؟™ن؛›ç®—و³•çڑ„详细وڈڈè؟°م€په®çژ°ن»£ç پوˆ–相ه…³ه®ن¾‹ï¼Œو·±ه…¥ه¦ن¹ è؟™ن؛›ه†…ه®¹ه°†وœ‰هٹ©ن؛ژو·±ه…¥çگ†è§£ه’Œه؛”用è؟™ن¸¤ç§چç®—و³•م€‚
**OMPç®—و³•** وک¯MPç®—و³•çڑ„ن¸€ن¸ھهڈکن½“,ه®ƒه¼•ه…¥ن؛†و£ن؛¤و€§ï¼Œهچ³هœ¨و¯ڈن¸€و¥è؟ن»£ن¸éƒ½هˆ 除ن¸ژه½“ه‰چو®‹ه·®و£ن؛¤çڑ„ه·²é€‰ه…ƒç´ ,ن»¥وڈگé«کé‡چو„ç²¾ه؛¦ه’Œè®،ç®—و•ˆçژ‡م€‚هœ¨MATLABن¸ï¼Œهڈ¯ن»¥و„ه»؛OMPç®—و³•çڑ„è؟ن»£و،†و¶ï¼ŒهŒ…و‹¬è®،ç®—و®‹ه·®م€پو‰¾هˆ°ç›¸ه…³ه؛¦وœ€é«کçڑ„هں؛ه…ƒç´ م€پ...
MP(Matching Pursuit, é…چه¯¹è؟½è¸ھ)ه’ŒOMP(Orthogonal Matching Pursuit, و£ن؛¤é…چه¯¹è؟½è¸ھ)وک¯هژ‹ç¼©و„ںçں¥ن¸ن¸¤ç§چه¸¸ç”¨çڑ„ن؟،هڈ·وپ¢ه¤چç®—و³•ï¼Œè؟™é‡Œوˆ‘ن»¬ن¸»è¦پ讨è®؛è؟™ن¸¤ن¸ھç®—و³•هڈٹه…¶هœ¨MATLABçژ¯ه¢ƒن¸‹çڑ„ه®çژ°م€‚ MPç®—و³•وک¯ن¸€ç§چè؟ن»£و–¹و³•ï¼Œه®ƒé€ڑè؟‡...
é€ڑè؟‡ه¯¹â€œOfdmOmp.mâ€è؟›è،Œه¦ن¹ ه’Œçگ†è§£ï¼Œوˆ‘ن»¬هڈ¯ن»¥و·±ه…¥وژŒوڈ،OFDMç³»ç»ںçڑ„ن؟،هڈ·ه¤„çگ†ه’ŒOMPç®—و³•çڑ„细èٹ‚,è؟™ه¯¹ن؛ژç ”ç©¶ه’Œه¼€هڈ‘و— ç؛؟é€ڑن؟،ç³»ç»ں,ه°¤ه…¶وک¯و¶‰هڈٹهˆ°ن؟،هڈ·هژ‹ç¼©ه’Œç¨€ç–ڈè،¨ç¤؛çڑ„هœ؛و™¯ï¼Œه…·وœ‰é‡چè¦پçڑ„çگ†è®؛ه’Œه®è·µن»·ه€¼م€‚
ن¸‹é¢ه°†è¯¦ç»†éکگè؟°MPه’ŒOMPç®—و³•çڑ„هژںçگ†م€په®çژ°و¥éھ¤ن»¥هڈٹه®ƒن»¬هœ¨MATLABçژ¯ه¢ƒن¸çڑ„ه؛”用م€‚ **هŒ¹é…چè؟½è¸ھ(MP)算و³•** هŒ¹é…چè؟½è¸ھç®—و³•و؛گن؛ژ1993ه¹´ï¼Œه®ƒوک¯ن¸€ç§چè؟ن»£ه¯»و‰¾وœ€ن½³هژںهگçڑ„ç–ç•¥م€‚MPçڑ„هں؛وœ¬و€وƒ³وک¯ن»ژن¸€ن¸ھه¤§çڑ„هژںهگ集هگˆن¸ï¼Œو¯ڈو¬،选و‹©ن¸ژ...
م€ٹو£ن؛¤هŒ¹é…چ Pursuit(OMP)算و³•هڈٹه…¶ن¼کهŒ–详解م€‹ و£ن؛¤هŒ¹é…چè؟½و±‚(Orthogonal Matching Pursuit,简称OMP)算و³•وک¯هژ‹ç¼©و„ںçں¥ï¼ˆCompressive Sensing,CS)领هںںن¸çڑ„ن¸€ç§چé‡چè¦پé‡چو„ç®—و³•ï¼Œه®ƒهœ¨هں؛ç،€çڑ„هŒ¹é…چè؟½è¸ھ(Matching Pursuit...
MP وک¯وœ€و—©çڑ„هژ‹ç¼©و„ںçں¥é‡چو„ç®—و³•ن¹‹ن¸€ï¼Œه…¶و ¸ه؟ƒو€وƒ³وک¯é€گو¥é€‰و‹©وœ€èƒ½è§£é‡ٹ观وµ‹و•°وچ®çڑ„ن؟،هڈ·هژںهگم€‚هœ¨و¯ڈو¬،è؟ن»£ن¸ï¼ŒMP 都ن¼ڑو‰¾هˆ°ن¸ژو®‹ه·®وœ€ç›¸ه…³çڑ„هژںهگ,ه°†ه…¶و·»هٹ هˆ°è§£ç©؛间,ه¹¶و›´و–°و®‹ه·®م€‚MP ç®—و³•ç®€هچ•وک“ه®çژ°ï¼Œن½†هœ¨é«که™ھه£°çژ¯ه¢ƒوˆ–é稀ç–ڈ...
OMPç®—و³•هں؛ن؛ژçں©éکµهˆ†è§£çڑ„و€وƒ³ï¼Œهپ‡è®¾وˆ‘ن»¬وœ‰ن¸€ن¸ھ观وµ‹çں©éکµAه’Œن¸€ن¸ھ观وµ‹ه€¼هگ‘é‡ڈb,目و ‡وک¯ه¯»و‰¾ن¸€ن¸ھ稀ç–ڈç³»و•°هگ‘é‡ڈx,ن½؟ه¾—Axه°½هڈ¯èƒ½وژ¥è؟‘bم€‚ç®—و³•çڑ„هں؛وœ¬و¥éھ¤ه¦‚ن¸‹ï¼ڑ 1. هˆه§‹هŒ–ï¼ڑ选و‹©ن¸€ن¸ھوœ€ه¤§و®‹ه·®و–¹هگ‘ن½œن¸؛第ن¸€ن¸ھو”¯وŒپهگ‘é‡ڈ,هچ³ç¬¬ن¸€ن¸ھé...
ه…³ن؛ژè´ھه©ھç®—و³•çڑ„MPم€پOMPçڑ„ه¤ڑه؟«و€•وœ€هں؛وœ¬çڑ„matlabن»؟çœںم€‚
é€ڑه¸¸ï¼Œوˆ‘ن»¬هڈ¯ن»¥هں؛ن؛ژ`sparsity`ه’Œ`corr`ç‰ه‡½و•°و¥و„ه»؛هں؛وœ¬çڑ„OMPç®—و³•م€‚ وœ€هگژ,BP,هچ³هڈچهگ‘ن¼ و’,وک¯و·±ه؛¦ه¦ن¹ ن¸وœ€ه¸¸ç”¨çڑ„ç¥ç»ڈ网络è®ç»ƒç®—و³•م€‚BPé€ڑè؟‡è®،ç®—وچںه¤±ه‡½و•°ç›¸ه¯¹ن؛ژوƒé‡چçڑ„و¢¯ه؛¦ï¼Œو¥و›´و–°ç½‘络çڑ„هڈ‚و•°ï¼Œن»ژ而وœ€ه°ڈهŒ–预وµ‹è¾“ه‡؛ن¸ژ...
OMPوک¯ن¸€ç§چç»ڈه…¸çڑ„هژ‹ç¼©و„ںçں¥وپ¢ه¤چç®—و³•ï¼Œه…¶و ¸ه؟ƒو€وƒ³وک¯هœ¨و¯ڈو¬،è؟ن»£ن¸و‰¾هˆ°ن¸€ن¸ھوœ€èƒ½è§£é‡ٹو®‹ه·®çڑ„هژںهگ,ه¹¶و£ن؛¤هŒ–ه…¶ن»–هژںهگن»¥ه‡ڈه°‘相ن؛’ه½±ه“چم€‚OMPهœ¨و•ˆçژ‡ه’Œé‡چو„è´¨é‡ڈن¹‹é—´هڈ–ه¾—ه¹³è،،,ه¹؟و³›ه؛”用ن؛ژه®é™…é—®é¢کن¸م€‚ 3. **WMP(Weighted ...
و–‡ç« وœ€هگژé€ڑè؟‡ه¯¹OMPç®—و³•ه’ŒMPç®—و³•çڑ„ن»؟çœں结وœè؟›è،Œه¯¹و¯”هˆ†وگ,éھŒè¯پن؛†OMPç®—و³•هœ¨è؟ن»£و”¶و•›و€§ه’Œه›¾هƒڈé‡چو„و•ˆوœن¸ٹ都وکژوک¾ن¼کن؛ژMPç®—و³•م€‚OMPç®—و³•çڑ„误ه·®هڈ¯ن»¥è¾¾هˆ°10çڑ„è´ںé‡ڈç؛§ï¼Œè€ŒMPç®—و³•çڑ„误ه·®ن¸؛10çڑ„é‡ڈç؛§م€‚ه¹¶ن¸”,OMPç®—و³•هœ¨ه›¾هƒڈé‡چه»؛è؟‡ç¨‹ن¸...
1. **هŒ¹é…چ pursuit (MP)**ï¼ڑMPç®—و³•وک¯وœ€هں؛وœ¬çڑ„é‡چو„و–¹و³•ن¹‹ن¸€ï¼Œه®ƒé€ڑè؟‡è؟ن»£é€‰و‹©ن¸ژو®‹ه·®وœ€ç›¸ه…³çڑ„هژںهگ(ن؟،هڈ·çڑ„هں؛ه…ƒç´ ),ه¹¶و›´و–°ن؟،هڈ·ن¼°è®،ه€¼ï¼Œç›´هˆ°è¾¾هˆ°é¢„设çڑ„è؟ن»£و¬،و•°وˆ–و®‹ه·®éکˆه€¼م€‚ 2. **و£ن؛¤هŒ¹é…چ pursuit (OMP)**ï¼ڑOMPوک¯ه¯¹MP...
MPç®—و³•م€پOMPç®—و³•é‡چو„ن¸€ç»´ن؟،هڈ·ن»£ç پ
و€»ç»“,هژ‹ç¼©و„ںçں¥ه›¾هƒڈé‡چه»؛وک¯ç»“هگˆن؛†و•°ه¦م€پç»ںè®،ه¦ه’Œè®،ç®—وœ؛科ه¦çڑ„ن؛¤هڈ‰é¢†هںں,IRLSه’ŒMPç®—و³•وک¯ه…¶ن¸é‡چè¦پçڑ„وپ¢ه¤چç–ç•¥م€‚é€ڑè؟‡ه¯¹è؟™ن؛›ç®—و³•çڑ„çگ†è§£ه’Œه®è·µï¼Œوˆ‘ن»¬هڈ¯ن»¥و›´و·±ه…¥هœ°وژŒوڈ،هژ‹ç¼©و„ںçں¥çڑ„精髓,ن¸؛ه®é™…ه؛”用وڈگن¾›çگ†è®؛و”¯وŒپم€‚
وœ¬و–‡ه°†و·±ه…¥وژ¢è®¨OMPç®—و³•هڈٹه…¶هœ¨ه›¾هƒڈوپ¢ه¤چه’Œé‡چو„ن¸çڑ„ه؛”用م€‚ 首ه…ˆï¼Œçگ†è§£OMPç®—و³•çڑ„هں؛وœ¬هژںçگ†è‡³ه…³é‡چè¦پم€‚OMPوک¯ن¸€ç§چè؟ن»£ç®—و³•ï¼Œç”¨ن؛ژه¯»و‰¾ç¨€ç–ڈè،¨ç¤؛,هچ³هœ¨وںگç§چهں؛وˆ–ه—ه…¸ن¸ï¼Œن؟،هڈ·هڈ¯ن»¥è¢«è،¨ç¤؛ن¸؛ه°‘و•°é零系و•°çڑ„ç؛؟و€§ç»„هگˆم€‚هœ¨و¯ڈن¸€è½®è؟ن»£...
相و¯”ن؛ژهں؛وœ¬çڑ„MPç®—و³•ï¼ŒOMPé€ڑه¸¸èƒ½èژ·ه¾—و›´ه¥½çڑ„é‡چو„è´¨é‡ڈه’Œو”¶و•›é€ںه؛¦م€‚ و€»ç»“èµ·و¥ï¼ŒهŒ¹é…چè؟½è¸ھ(MP)算و³•ه’Œه…¶هڈکç§چو£ن؛¤هŒ¹é…چè؟½è¸ھ(OMP)وک¯è§£ه†³ç¨€ç–ڈè،¨ç¤؛é—®é¢کçڑ„é‡چè¦په·¥ه…·ï¼Œه®ƒن»¬é‡‡ç”¨è´ھه©ھç–ç•¥é€گو¥و„ه»؛ن؟،هڈ·çڑ„è؟‘ن¼¼è،¨ç¤؛,ه…·وœ‰è¾ƒé«کçڑ„è®،ç®—...
é€ڑè؟‡è؟گè،Œه’Œهˆ†وگè؟™ن¸ھ程ه؛ڈ,用وˆ·ن¸چن»…هڈ¯ن»¥ن؛†è§£ç¨€ç–ڈè،¨ç¤؛çڑ„هں؛وœ¬و€وƒ³ï¼Œè؟ک能و·±ه…¥çگ†è§£MPç®—و³•çڑ„ه·¥ن½œهژںçگ†ï¼Œه¹¶هڈ¯è؟›ن¸€و¥وژ¢ç´¢ن¼کهŒ–ه’Œو”¹è؟›çڑ„هڈ¯èƒ½و€§ï¼Œو¯”ه¦‚ه¼•ه…¥و›´ه…ˆè؟›çڑ„ç®—و³•ه¦‚OMP( Orthogonal Matching Pursuit,و£ن؛¤هŒ¹é…چè؟½è¸ھ)وˆ–...
هœ¨وœ¬هژ‹ç¼©هŒ…و–‡ن»¶â€œMP相ه…³ç®—و³•.zipâ€ن¸ï¼ŒهŒ…هگ«ن؛†ن»¥ن¸‹ه‡ ç§چه¸¸è§پçڑ„MPç®—و³•ه®çژ°ï¼ڑ 1. OMP(Orthogonal Matching Pursuit,و£ن؛¤هŒ¹é…چè؟½è¸ھ)ï¼ڑ OMPوک¯ن¸€ç§چè؟ن»£ç®—و³•ï¼Œو¯ڈو¬،è؟ن»£ن¸ï¼Œه®ƒن¼ڑو‰¾هˆ°ن¸ژو®‹ه·®وœ€ç›¸ه…³çڑ„ه—ه…¸هژںهگ,ه¹¶ه°†ه…¶و·»هٹ هˆ°...