- 浏览: 1415810 次
- 性别:

- 来自: 广州
-

文章分类
最新评论
-
sdgxxtc:
[quo[color=red]te][/color]
C#使用OleDb读取Excel,生成SQL语句 -
zcs302567601:
博主,你好,一直都有个问题没有搞明白,就是 2.x的版本是通过 ...
NGUI所见即所得之UIPanel -
一样的追寻:
感谢楼主!
有向强连通和网络流大讲堂——史无前例求解最大流(最小割)、最小费用最大流 -
cp1993518:
感谢!从你的博客里学到了很多
Unity日志工具——封装,跳转 -
cp1993518:
学习了~,话说现在的版本custom还真的变委托了
NGUI所见即所得之UIGrid & UITable
红黑树(Red-Black Tree)
红黑树定义
红黑树是每个节点都带有颜色属性的二叉查找树,颜色为红色或黑色。在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
性质1. 节点是红色或黑色。
性质2. 根是黑色。
性质3. 所有叶子都是黑色(叶子是NIL节点)。
性质4. 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
性质5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
下面先给出红黑树的抽象数据类型
#ifndef RBT_H
#define RBT_H
typedef enum {
RBT_STATUS_OK,
RBT_STATUS_MEM_EXHAUSTED,
RBT_STATUS_DUPLICATE_KEY,
RBT_STATUS_KEY_NOT_FOUND
} RbtStatus;
typedef void *RbtIterator;
typedef void *RbtHandle;
RbtHandle rbtNew(int(*compare)(void *a, void *b));
// create red-black tree
// parameters:
// compare pointer to function that compares keys
// return 0 if a == b
// return < 0 if a < b
// return > 0 if a > b
// returns:
// handle use handle in calls to rbt functions
void rbtDelete(RbtHandle h);
// destroy red-black tree
RbtStatus rbtInsert(RbtHandle h, void *key, void *value);
// insert key/value pair
RbtStatus rbtErase(RbtHandle h, RbtIterator i);
// delete node in tree associated with iterator
// this function does not free the key/value pointers
RbtIterator rbtNext(RbtHandle h, RbtIterator i);
// return ++i
RbtIterator rbtBegin(RbtHandle h);
// return pointer to first node
RbtIterator rbtEnd(RbtHandle h);
// return pointer to one past last node
void rbtKeyValue(RbtHandle h, RbtIterator i, void **key, void **value);
// returns key/value pair associated with iterator
RbtIterator rbtFind(RbtHandle h, void *key);
// returns iterator associated with key
#endif
红黑树平衡化旋转
红黑树的旋转操作没有AVL树那么复杂,这里的旋转也不区分结点的颜色,纯粹是旋转移动结点的位置,即只有两种操作——左旋和右旋。
1.左旋
![红黑树的介绍和实现[原创] - saturnman - 一路](http://img.ph.126.net/qpfZHL16Cjw_RyOm1xP_Cg==/2313724308562050452.jpg)
static void rotateLeft(RbtType *rbt, NodeType *x) {
// rotate node x to left
NodeType *y = x->right;
// establish x->right link
x->right = y->left;
if (y->left != SENTINEL) y->left->parent = x;
// establish y->parent link
if (y != SENTINEL) y->parent = x->parent;
if (x->parent) {
if (x == x->parent->left)
x->parent->left = y;
else
x->parent->right = y;
} else {
rbt->root = y;
}
// link x and y
y->left = x;
if (x != SENTINEL) x->parent = y;
}
2.右旋
![红黑树的介绍和实现[原创] - saturnman - 一路](http://img314.ph.126.net/_W4bx4oCFnzi7r5LEXUz-A==/3880695503910237838.jpg)
static void rotateRight(RbtType *rbt, NodeType *x) {
// rotate node x to right
NodeType *y = x->left;
// establish x->left link
x->left = y->right;
if (y->right != SENTINEL) y->right->parent = x;
// establish y->parent link
if (y != SENTINEL) y->parent = x->parent;
if (x->parent) {
if (x == x->parent->right)
x->parent->right = y;
else
x->parent->left = y;
} else {
rbt->root = y;
}
// link x and y
y->right = x;
if (x != SENTINEL) x->parent = y;
}
红黑树的插入和删除
1. 插入操作
我们总是插入红色的节点,因为这样就可以在插入过程中尽量避免产生对树的调整,我们新插入一个节点后可能使原树的哪些性质改变呢。由于我们是按二叉树的方式插入,因此原树的搜索性质不会改变。如果插入的节点是根节点,性质2会被破坏,如果插入的节点的父节点是红色,则会破坏性质4,因此总的来说,插入一个红色节点只会破坏到性质2或是性质4,我们的恢复树性质的策略很简单,其一就是保持一定的性质不变,之后把出现违背红黑树性质地方向上移,如果能移到根节点,那么很容易就可以通过直接修改根节点来恢复红黑树应满足的性质。其二就是穷举所有的可能性,之后把能归于同一类方法处理的归为同一类,不能直接处理的化归到其它可以直接处理的情况,能直接处理的就直接处理。
下面看看一共有几种情况,
情况1:插入的是根节点(原树是空树)
此情况只会违反性质2。
解法:直接把此节点涂为黑色
情况2:插入的节点的的父节点是黑色
此时不会违反性质2也不会违反性质4,红黑树没有被破坏。
解法:什么都不做
情况3:当前节点的父节点是红色且祖父节点的另一个子节点(叔叔节点)是红色(此时父节点的父节点一定存在,否则插入前就已不是红黑树,此时又分为父节点是祖父节点的左子或者右子,对于对称性,只要解开一个方向就可以了,我们只考虑父节点为祖父左子的情况)。此时还可分为当前节点是其父节点的左子还是右子,但是这两种情况的处理方式是一样的,我们将其归为同一类。
解法:将当前节点的父节点和叔叔节点涂黑,祖父结点涂红,把当前结点指向祖父节点,从新的当前节点重新开始算法。
变换前
![红黑树的介绍和实现[原创] - saturnman - 一路](http://img317.ph.126.net/uC3ZyCygH0LQycTAWgWviQ==/3772327637876476283.png)
变换后
![红黑树的介绍和实现[原创] - saturnman - 一路](http://img.ph.126.net/Rslmy5O91SGaYDJWu_47_w==/3053440547357758784.png)
情况4:当前节点的父节点是红色,叔叔节点是黑色,当前节点是其父节点的右子
解法:当前节点的父节点做为新的当前节点,以新当前节点为支点左旋。
如下图所示
变换前
![红黑树的介绍和实现[原创] - saturnman - 一路](http://img.ph.126.net/Rslmy5O91SGaYDJWu_47_w==/3053440547357758784.png)
变换后
![红黑树的介绍和实现[原创] - saturnman - 一路](http://img.ph.126.net/BLjF0lUMo8LwjCfdkTqKag==/3390084619504294102.png)
情况5:当前节点的父节点是红色,叔叔节点是黑色,当前节点是其父节点的左子
解法:父节点变为黑色,祖父节点变为红色,在祖父节点为支点右旋
如下图所示
变换前
![红黑树的介绍和实现[原创] - saturnman - 一路](http://img.ph.126.net/BLjF0lUMo8LwjCfdkTqKag==/3390084619504294102.png)
变换后
![红黑树的介绍和实现[原创] - saturnman - 一路](http://img.ph.126.net/Fbxv7rvCWc4MLk1bhUPvOg==/3694077594351108642.png)
在上面的插入算法中,所有递归都是尾递归,可以改写为循环,其中以当前节点的父节点是否为红色是十分方便的。
2.删除操作
我们删除的节点的方法与常规二叉搜索树中删除节点的方法是一样的,如果被删除的节点不是有双非空子女,则直接删除这个节点,用它的唯一子节点顶替它的位置,如果它的子节点分是空节点,那就用空节点顶替它的位置,如果它的双子全为非空,我们就把它的直接后继节点内容复制到它的位置,之后以同样的方式删除它的后继节点,它的后继节点不可能是双子非空,因此此传递过程最多只进行一次。在册除节点后,原红黑树的性质可能被改变,如果删除的是红色节点,那么原红黑树的性质依旧保持,此时不用做修正操作,如果删除的节点是黑色节点,原红黑树的性质可能会被改变,我们要对其做修正操作。那么哪些树的性质会发生变化呢,如果删除节点不是树唯一节点,那么删除节点的那一个支的到各叶节点的黑色节点数会发生变化,此时性质5被破坏。如果被删节点的唯物主唯一非空子节点是红色,而被删节点的父节点也是红色,那么性质4被破坏。如果被删节点是根节点,而它的唯一非空子节点是红色,则删除后新根节点将变成红色,违背性质2。现在情况看起来有些复杂,这里面我们用一个分析技巧,这引技巧是从《算法导论》一书中学来的。我们从被删节点后来顶替它的那个节点开始调整,并认为它有额外的一重黑色。这里额外一重黑色是什么意思呢,我们不是把红黑树的节点加上除红与黑的另一种颜色,这里只是一种假设,我们认为我们当前指向它,因此空有额外一种黑色,可以认为它的黑色是从它的父节点被删除后继承给它的,它现在可以容纳两种颜色,如果它原来是红色,那么现在是红+黑,如果原来是黑色,那么它现在的颜色是黑+黑。有了这重额外的黑色,原红黑树性质5就能保持不变。现在只要花时是恢复其它性质就可以了,做法还是尽量向根移动和穷举所有可能性。
情况1:当前节点是红+黑色
解法,直接把当前节点染成黑色,结束。
此时红黑树性质全部恢复。
情况2:当前节点是黑+黑且是根节点
解法:什么都不做,结束
情况3:当前节点是黑+黑且兄弟节点为红色(此时父节点和兄弟节点的子节点分为黑)。
解法:把父节点染成红色,把兄弟结点染成黑色,之后重新进入算法(我们只讨论当前节点是其父节点左孩子时的情况)。此变换后原红黑树性质5不变,而把问题转化为兄弟节点为黑色的情况。
变换前
![红黑树的介绍和实现(一)[原创] - saturnman - 一路](http://img319.ph.126.net/0alMdc8ifgdkZzgJjAnHwA==/3830874433032271630.jpg)
变换后
![红黑树的介绍和实现(一)[原创] - saturnman - 一路](http://img319.ph.126.net/1B2SsaENmSPlDk7son5PCg==/3840163107263724527.jpg)
情况4:当前节点是黑加黑且兄弟是黑色且兄弟节点的两个子节点全为黑色
解法:把当前节点和兄弟节点中抽取一重黑色追加到父节点上,把父节点当成新的当前节点,重新进入算法。(此变换后性质5不变)
变换前
![红黑树的介绍和实现(一)[原创] - saturnman - 一路](http://img.ph.126.net/KNqv8BRU2D601cnKzhnDUQ==/3727573116579682852.jpg)
变换后
![红黑树的介绍和实现(一)[原创] - saturnman - 一路](http://img.ph.126.net/x0PLvuJxbqSWgzGvHvGKFQ==/3202622285014346969.jpg)
情况5:当前节点颜色是黑+黑,兄弟节点是黑色,兄弟的左子是红色,右子是黑色。
解法:把兄弟结点染红,兄弟左子节点染黑,之后再在兄弟节点为支点解右旋,之后重新进入算法。此是把当前的情况转化为情况6,而性质5得以保持。
变换前
![红黑树的介绍和实现(一)[原创] - saturnman - 一路](http://img.ph.126.net/wyogL9on4zwK5b300BU0zQ==/3261732030124697864.jpg)
变换后
![红黑树的介绍和实现(一)[原创] - saturnman - 一路](http://img.ph.126.net/6MPBFFyO5M-ZQrakWD7U0A==/952229846212680846.jpg)
情况6:当前节点颜色是黑-黑,它的兄弟节点是黑色,但是兄弟节点的右子是红色,兄弟节点左子的颜色任意。
解法:把兄弟节点染成当前节点父节点的颜色,把当前节点父节点染成黑色,兄弟节点右子染成黑色,之后以当前节点的父节点为支点进行左旋,此时算法结束,红黑树所有性质调整正确。
![红黑树的介绍和实现(一)[原创] - saturnman - 一路](http://img.ph.126.net/Gfexgoeuq1FG1X85ruoLiA==/3280872328541010228.jpg)
变换后
![红黑树的介绍和实现(一)[原创] - saturnman - 一路](http://img.ph.126.net/OV0GgAjos0OMcN92QBvSXA==/3374322020808370458.jpg)
红黑树的高度分析
包含n个内部节点的红黑树的高度是 O(log(n))。
定义:
- h(v) = 以节点v为根的子树的高度。
- bh(v) = 从v到子树中任何叶子的黑色节点的数目(如果v是黑色则不计数它)(也叫做黑色高度)。
引理: 以节点v为根的子树有至少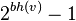 个内部节点。
个内部节点。
引理的证明(通过归纳高度):
基础: h(v) = 0
如果v的高度是零则它必定是 nil,因此 bh(v) = 0。所以:
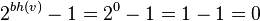
归纳假设: h(v) = k 的v有  个内部节点暗示了 h(
个内部节点暗示了 h(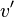 ) = k+1 的
) = k+1 的 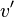 有
有 个内部节点。
个内部节点。
因为 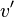 有 h(
有 h(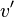 ) > 0 所以它是个内部节点。同样的它有黑色高度要么是 bh(
) > 0 所以它是个内部节点。同样的它有黑色高度要么是 bh(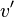 ) 要么是 bh(
) 要么是 bh(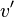 )-1 (依据
)-1 (依据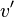 是红色还是黑色)的两个儿子。通过归纳假设每个儿子都有至少
是红色还是黑色)的两个儿子。通过归纳假设每个儿子都有至少  个内部接点,所以
个内部接点,所以 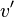 有:
有:

个内部节点。
使用这个引理我们现在可以展示出树的高度是对数性的。因为在从根到叶子的任何路径上至少有一半的节点是黑色(根据红黑树属性4),根的黑色高度至少是h(root)/2。通过引理我们得到:
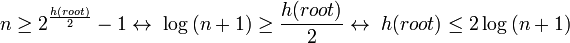
因此根的高度是O(log(n))。
下面附上完整的实现代码
// red-black tree
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <stdarg.h>
//////////////////////
// supplied by user //
//////////////////////
typedef int KeyType; // type of key
typedef struct { // value related to key
int stuff;
} ValType;
// how to compare keys
#define compLT(a,b) (a < b)
#define compEQ(a,b) (a == b)
/////////////////////////////////////
// implementation independent code //
/////////////////////////////////////
typedef enum {
RBT_STATUS_OK,
RBT_STATUS_MEM_EXHAUSTED,
RBT_STATUS_DUPLICATE_KEY,
RBT_STATUS_KEY_NOT_FOUND
} RbtStatus;
typedef enum { BLACK, RED } nodeColor;
typedef struct NodeTag {
struct NodeTag *left; // left child
struct NodeTag *right; // right child
struct NodeTag *parent; // parent
nodeColor color; // node color (BLACK, RED)
KeyType key; // key used for searching
ValType val; // data related to key
} NodeType;
#define SENTINEL &sentinel // all leafs are sentinels
static NodeType sentinel = { SENTINEL, SENTINEL, 0, BLACK, 0};
static NodeType *root = SENTINEL; // root of red-black tree
static void rotateLeft(NodeType *x) {
// rotate node x to left
NodeType *y = x->right;
// establish x->right link
x->right = y->left;
if (y->left != SENTINEL) y->left->parent = x;
// establish y->parent link
if (y != SENTINEL) y->parent = x->parent;
if (x->parent) {
if (x == x->parent->left)
x->parent->left = y;
else
x->parent->right = y;
} else {
root = y;
}
// link x and y
y->left = x;
if (x != SENTINEL) x->parent = y;
}
static void rotateRight(NodeType *x) {
// rotate node x to right
NodeType *y = x->left;
// establish x->left link
x->left = y->right;
if (y->right != SENTINEL) y->right->parent = x;
// establish y->parent link
if (y != SENTINEL) y->parent = x->parent;
if (x->parent) {
if (x == x->parent->right)
x->parent->right = y;
else
x->parent->left = y;
} else {
root = y;
}
// link x and y
y->right = x;
if (x != SENTINEL) x->parent = y;
}
static void insertFixup(NodeType *x) {
// maintain red-black tree balance
// after inserting node x
// check red-black properties
while (x != root && x->parent->color == RED) {
// we have a violation
if (x->parent == x->parent->parent->left) {
NodeType *y = x->parent->parent->right;
if (y->color == RED) {
// uncle is RED
x->parent->color = BLACK;
y->color = BLACK;
x->parent->parent->color = RED;
x = x->parent->parent;
} else {
// uncle is BLACK
if (x == x->parent->right) {
// make x a left child
x = x->parent;
rotateLeft(x);
}
// recolor and rotate
x->parent->color = BLACK;
x->parent->parent->color = RED;
rotateRight(x->parent->parent);
}
} else {
// mirror image of above code
NodeType *y = x->parent->parent->left;
if (y->color == RED) {
// uncle is RED
x->parent->color = BLACK;
y->color = BLACK;
x->parent->parent->color = RED;
x = x->parent->parent;
} else {
// uncle is BLACK
if (x == x->parent->left) {
x = x->parent;
rotateRight(x);
}
x->parent->color = BLACK;
x->parent->parent->color = RED;
rotateLeft(x->parent->parent);
}
}
}
root->color = BLACK;
}
// insert new node (no duplicates allowed)
RbtStatus rbtInsert(KeyType key, ValType val) {
NodeType *current, *parent, *x;
// allocate node for data and insert in tree
// find future parent
current = root;
parent = 0;
while (current != SENTINEL) {
if (compEQ(key, current->key))
return RBT_STATUS_DUPLICATE_KEY;
parent = current;
current = compLT(key, current->key) ?
current->left : current->right;
}
// setup new node
if ((x = malloc (sizeof(*x))) == 0)
return RBT_STATUS_MEM_EXHAUSTED;
x->parent = parent;
x->left = SENTINEL;
x->right = SENTINEL;
x->color = RED;
x->key = key;
x->val = val;
// insert node in tree
if(parent) {
if(compLT(key, parent->key))
parent->left = x;
else
parent->right = x;
} else {
root = x;
}
insertFixup(x);
return RBT_STATUS_OK;
}
static void deleteFixup(NodeType *x) {
// maintain red-black tree balance
// after deleting node x
while (x != root && x->color == BLACK) {
if (x == x->parent->left) {
NodeType *w = x->parent->right;
if (w->color == RED) {
w->color = BLACK;
x->parent->color = RED;
rotateLeft (x->parent);
w = x->parent->right;
}
if (w->left->color == BLACK && w->right->color == BLACK) {
w->color = RED;
x = x->parent;
} else {
if (w->right->color == BLACK) {
w->left->color = BLACK;
w->color = RED;
rotateRight (w);
w = x->parent->right;
}
w->color = x->parent->color;
x->parent->color = BLACK;
w->right->color = BLACK;
rotateLeft (x->parent);
x = root;
}
} else {
NodeType *w = x->parent->left;
if (w->color == RED) {
w->color = BLACK;
x->parent->color = RED;
rotateRight (x->parent);
w = x->parent->left;
}
if (w->right->color == BLACK && w->left->color == BLACK) {
w->color = RED;
x = x->parent;
} else {
if (w->left->color == BLACK) {
w->right->color = BLACK;
w->color = RED;
rotateLeft (w);
w = x->parent->left;
}
w->color = x->parent->color;
x->parent->color = BLACK;
w->left->color = BLACK;
rotateRight (x->parent);
x = root;
}
}
}
x->color = BLACK;
}
// delete node
RbtStatus rbtErase(NodeType * z) {
NodeType *x, *y;
if (z->left == SENTINEL || z->right == SENTINEL) {
// y has a SENTINEL node as a child
y = z;
} else {
// find tree successor with a SENTINEL node as a child
y = z->right;
while (y->left != SENTINEL) y = y->left;
}
// x is y's only child
if (y->left != SENTINEL)
x = y->left;
else
x = y->right;
// remove y from the parent chain
x->parent = y->parent;
if (y->parent)
if (y == y->parent->left)
y->parent->left = x;
else
y->parent->right = x;
else
root = x;
if (y != z) {
z->key = y->key;
z->val = y->val;
}
if (y->color == BLACK)
deleteFixup (x);
free (y);
return RBT_STATUS_OK;
}
// find key
NodeType *rbtFind(KeyType key) {
NodeType *current;
current = root;
while(current != SENTINEL) {
if(compEQ(key, current->key)) {
return current;
} else {
current = compLT (key, current->key) ?
current->left : current->right;
}
}
return NULL;
}
// in-order walk of tree
void rbtInorder(NodeType *p, void (callback)(NodeType *)) {
if (p == SENTINEL) return;
rbtInorder(p->left, callback);
callback(p);
rbtInorder(p->right, callback);
}
// delete nodes depth-first
void rbtDelete(NodeType *p) {
if (p == SENTINEL) return;
rbtDelete(p->left);
rbtDelete(p->right);
free(p);
}
void displayNode(NodeType *p) {
printf("%d %d\n", p->key, p->val.stuff);
}
int main(int argc, char **argv) {
int maxnum, ct;
KeyType key;
RbtStatus status;
// command-line:
//
// rbt 2000
// process 2000 records
NodeType *p;
maxnum = atoi(argv[1]);
printf("maxnum = %d\n", maxnum);
for (ct = maxnum; ct; ct--) {
key = rand() % 90 + 1;
if ((p = rbtFind(key)) != NULL) {
if (p->val.stuff != 10*key) printf("fail val\n");
status = rbtErase(p);
if (status) printf("fail: status = %d\n", status);
} else {
ValType val;
val.stuff = 10*key;
status = rbtInsert(key, val);
if (status) printf("fail: status = %d\n", status);
}
}
// output nodes in order
rbtInorder(root, displayNode);
rbtDelete(root);
return 0;
}
参考:
①Implementation in C: http://epaperpress.com/sortsearch/txt/rbt.txt
②维基百科: http://zh.wikipedia.org/zh/%E7%BA%A2%E9%BB%91%E6%A0%91
③http://epaperpress.com/sortsearch/rbt.html
④saturnma: http://saturnman.blog.163.com/blog/static/5576112010969420383/
发表评论
-
C# 调用Delegate.CreateDelegate方法出现“未处理ArgumentException”错误解决
2013-05-31 12:24 3603在C# 调用Delegate.Create ... -
数组问题集结号
2012-12-06 22:01 0数组是最简单的数据结构,数组问题作为公司招聘的笔试和面试题目 ... -
算法问题分析笔记
2012-12-05 11:59 01.Crash Balloon Zhejiang Univer ... -
Java基础进阶整理
2012-11-26 09:59 2353Java学习笔记整理 ... -
Java学习笔记整理
2012-11-24 23:43 211Java学习笔记整理 本文档是我个人 ... -
《C++必知必会》学习笔记
2012-11-24 23:40 2671《C++必知必会》学� ... -
《C++必知必会》学习笔记
2012-11-24 23:34 1《C++必知必会》学习笔� ... -
C语言名题精选百则——排序
2012-11-04 23:29 128第5章排 序 问题5.1 二分插入法(BIN ... -
C语言名题精选百则——查找
2012-11-04 23:29 4188尊重他人的劳动,支持原创 本篇博文,D.S.Q ... -
基本技术——贪心法、分治法、动态规划三大神兵
2012-11-03 19:30 0基本技术——贪心法、分治法、动态规划三大神兵 -
优先队列三大利器——二项堆、斐波那契堆、Pairing 堆
2012-11-03 13:12 35713优先队列三大利器——二项堆、斐波那契堆、Pairing ... -
优先队列三大利器——二项堆、斐波那契堆、Pairing 堆
2012-11-03 13:01 3优先队列三大利器——二项堆、斐波那契堆、Pairing 堆 ... -
排序算法群星豪华大汇演
2012-10-30 00:09 3187排序算法群星豪华大汇演 排序算法相对简单些,但是由于 ... -
分布排序(distribution sorts)算法大串讲
2012-10-29 15:33 4700分布排序(distribution sorts)算法大串讲 ... -
归并排序(merge sorts)算法大串讲
2012-10-29 10:04 8347归并排序(merge sorts)算法大串讲 ... -
交换排序(exchange sorts)算法大串讲
2012-10-29 00:22 4444交换排序(exchange sorts)算法大串讲 本 ... -
选择排序(selection sorts)算法大串讲
2012-10-28 12:55 3758选择排序(selection sorts)算法大串讲 本文内 ... -
插入排序(insertion sorts)算法大串讲
2012-10-28 11:30 2781插入排序(insertion sorts� ... -
伸展树(Splay Tree)尽收眼底
2012-10-27 15:11 5617伸展树(Splay Tree)尽收眼底 本文内容 ... -
平衡二叉树(AVL)原理透析和编码解密
2012-10-26 10:22 3043平衡二叉树(AVL)原理透析和编码解密 本文内容 ...









相关推荐
红黑树(Red-Black Tree)是二叉搜索树(Binary Search Tree)的一种改进。我们知道二叉搜索树在最坏的情况下可能会变成一个链表(当所有节点按从小到大的顺序依次插入后)。而红黑树在每一次插入或删除节点 之后...
红黑树(Red-Black Tree)是一种自平衡二叉查找树,它在计算机科学中用于实现关联数组。这种数据结构最初由Rudolf Bayer在1972年发明,当时称为“对称二叉B树”,但在1978年由Leonidas J. Guibas和Robert Sedgewick...
这一版代码个人认为99.99%正确,本人使用些结构及算法用于实现嵌入式迅雷Server的任务管理。此代码经本人学习研究之后从C语言版BT源代码中的宏定义式代码中分离出来,并做成一...希望对需要学习红黑树的人有帮助。
红黑树(Red-Black Tree)是一种自平衡二叉查找树,由IBM的研究员鲁道夫·贝尔在1972年提出。它的设计目标是在插入、删除和查找操作上保持近似最坏情况下的O(log n)时间复杂度,同时通过特定的颜色规则保证树的平衡...
红黑树(Red-Black Tree)是一种自平衡的二叉搜索树,它在传统的二叉搜索树的基础上增加了一个颜色属性,用于确保树在插入和删除操作后仍然保持大致平衡。这种平衡性是通过一系列的旋转和重新着色操作来实现的,以...
红黑树(Red-Black Tree)是一种自平衡二叉查找树,由Rudolf Bayer在1972年提出,它的每个节点都带有颜色属性,可以是红色或黑色。这种数据结构在计算机科学中有着广泛的应用,特别是在实现关联数组、数据库索引、...
标题中的"Python库 | red-black-tree-mod-1.11.tar.gz"指的是一种基于Python实现的红黑树数据结构的库,版本为1.11,并被打包成tar.gz格式的压缩文件。红黑树是一种自平衡二叉查找树,它的设计目标是保证在进行插入...
红黑树(Red-Black Tree)是一种自平衡二叉查找树,由计算机科学家Rudolf Bayer在1972年提出。它在保持二叉查找树特性的同时,通过额外的颜色属性来实现对树的调整,使得插入、删除和查找操作的时间复杂度在最坏情况...
Red-black tree the Linux kernel package with a omnipotent red-black tree how to use: see rbtest1.c and rbtest2.c Directly generate rbtest1 and rbtest2 make You can modify and run author: rcyh ...
红黑树(Red-Black Tree)是一种自平衡二叉查找树,由计算机科学家Rudolf Bayer在1972年提出。它的名字来源于节点可能有的两种颜色:红色或黑色。红黑树的主要特性保证了其在操作上的高效性,如插入、删除和查找等...
红黑树(Red Black Tree)是一种自平衡二叉查找树,由计算机科学家Rudolf Bayer在1972年提出。这种数据结构在现代计算机科学中广泛应用,特别是在各种需要高效查找、插入和删除操作的场景中。红黑树的主要特点是通过...
这个RAR压缩包包含了一个名为"Proyecto - DAA - Eliminacion en un RED-BLACK_TREE"的文件,很可能是关于红色-黑色树在数据结构与算法分析(DAA)课程中的一个项目,特别是关于在红黑树中执行删除操作的探讨。...
红黑树C语言代码: #include "redblack.h" #include #include "fatal.h" 头文件: #include #include "fatal.h" typedef int ElementType; #define NegInfinity (-10000) #ifndef _RedBlack_H #define _Red...
红黑树 这是Ada 2012对(一种自平衡二进制搜索树)的实现。 该树使用标准的Ada.Iterator_Interfaces进行迭代。 with Ada.Integer_Text_IO ; use Ada.Integer_Text_IO; with Ada.Text_IO ; use Ada.Text_IO; with ...
红黑树(Red-Black Tree)是一种自平衡二叉查找树,由计算机科学家Rudolf Bayer于1972年提出。它在数据结构中扮演着重要的角色,特别是在需要高效插入、删除和查找操作的场景下。红黑树在C语言和C++编程中被广泛应用...
红黑树,详细的代码过程,完整的代码实现,希望对大家有帮助,第一次上传,为了赚积分,
红黑树(Red-Black Tree)是一种自平衡的二叉查找树。在红黑树中,每个节点包含一个颜色属性,可以是红色或黑色。通过对任何一条从根到叶子的路径上各个节点的颜色进行约束,红黑树确保没有一条路径会比其他路径长出...
"test_red_black_tree.cc"是一个测试文件,可能包含了针对红黑树实现的各种测试用例,用于验证算法的正确性。 "red_black_tree.h"是头文件,它定义了红黑树的数据结构和公开的接口,供其他模块调用。 "stack.h"是...
红黑树(Red-Black Tree)是一种自平衡二叉查找树,在计算机科学领域有着广泛的应用,尤其是在实现关联数组方面。作为一种高效的查找、插入与删除操作的数据结构,红黑树能够保持较高的性能,最坏情况下的时间复杂度...
红黑树是计算机科学中的一种自平衡二叉查找树,它在插入和删除操作时,通过旋转和重新着色的方式,保持树的平衡,确保最长路径不会超过最短路径的两倍。这种特性使得红黑树在最坏情况下也能保持对数时间的复杂度。...