二叉排序树（二叉查找树）介绍

1.简介

二叉查找树（Binary Search Tree），或者是一棵空树，或者是具有下列性质的二叉树：

1. 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
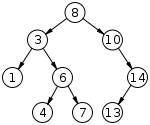
2. 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
3. 它的左、右子树也分别为二叉排序树。

中序遍历二叉排序树可得到一个关键字的有序序列，一个无序序列可以通过构造一棵二叉排序树变成一个有序序列，构造树的过程即为对无序序列进行排序的过程。每次插入的新的结点都是二叉排序树上新的叶子结点，在进行插入操作时，不必移动其它结点，只需改动某个结点的指针，由空变为非空即可。

搜索,插入,删除的复杂度等于树高，期望O(logn),最坏O(n)(数列有序,树退化成线性表).

 

虽然二叉排序树的最坏效率是O(n),但它支持动态查询,且有很多改进版的二叉排序树可以使树高为O(logn),如SBT,AVL,红黑树等.故不失为一种好的动态排序方法.

 

2.查找算法

 

在二叉排序树b中查找x的过程为：

1. 若b是空树，则搜索失败，否则：
2. 若x等于b的根节点的数据域之值，则查找成功；否则：
3. 若x小于b的根节点的数据域之值，则搜索左子树；否则：
4. 查找右子树。

 

/*
* b为二叉排序树根节点
* data为要查找元素
* f为搜索结果的双亲
* p为搜索结果节点
* 搜索成功返回true，否则返回false
*/
bool findElement(BT * b , dataType data,BT * f ,BT * p ){
     if(!b){
          return false;
     }
     if(data == b->data){
          p=b;
	  return true;
     }
     if(data> b->data){
          return findElement(b->rchild ,data,b ,p);
     }else{
           return findElement(b->lchild ,data,b ,p);
     }
}

 

 

 

3.插入算法

 

向一个二叉排序树b中插入一个结点s的算法，过程为：

1. 若b是空树，则将s所指结点作为根结点插入，否则：
2. 若s->data等于b的根结点的数据域之值，则返回，否则：
3. 若s->data小于b的根结点的数据域之值，则把s所指结点插入到左子树中，否则：
4. 把s所指结点插入到右子树中。

 

/*
* b为二叉排序树根节点
* data为要插入的元素
* 插入成功返回true，存在相同的则返回false
*/
bool insertElement(BT * b , dataType data){
     if(!b){
          b = new BT(data);
          b->lchild = null;
          b->rchild = null;
          return true;
     }
     if(data == b->data){
          //存在相同节点
	  return false;
     }
     if(data > b->data){
          return insertElement(b->rchild ,data);
     }else{
           return insertElement(b->lchild ,data);
     }
}

 

4.删除算法

 

在二叉排序树删除一个结点，设要删除的节点为p，其左子树为lc，右子树为rc其双亲节点为f，分三种情况讨论：

1. 若*p结点为叶子结点，即lc(左子树)和rc(右子树)均为空树。由于删去叶子结点不破坏整棵树的结构，则只需修改其双亲结点的指针即可。
2. 若*p结点只有左子树lc或只有右子树rc，此时只要令lc或rc直接成为其双亲结点*f的左子树（当*p是左子树）或右子树（当*p是右子树）即可，作此修改也不破坏二叉排序树的特性。
3. 若*p结点的左子树和右子树均不空。在删去*p之后，为保持其它元素之间的相对位置不变，可按中序遍历保持有序进行调整，可以有两种做法：其一是令*p的左子树为*f的左/右(依*p是*f的左子树还是右子树而定)子树，*s为*p左子树的最右下的结点（也就是最大的点），而*p的右子树为*s的右子树（相当于原来p的右子树接上了原来p的左子树中最右，也就是最大的节点，并作为其右子树）；其二是为了保证中序遍历的顺序，用*p的直接前驱（或直接后继）替代*p，然后再从二叉排序树中删去它的直接前驱（或直接后继）。

 

 

/*
* b为二叉排序树根节点
* data为要删除元素
* 删除成功返回true，否则返回false
*/
bool deleteElement(BT * b , dataType data){
    if(!b){
        return false;
    }
    if(data == b -> data){
        deleteBTNode(b);
        return true;
    }
    if(data > b -> data){
        deleteElement(b -> rchild , data);
    }else{
        deleteElement(b -> lchild , data); 
    }
}

void deleteBTNode(BT *p){
    if(!p -> lchild){
        //左子树为空,连接其右子树
        q = p -> rchild ;
        *p = *q; //这里赋值，可能会有问题，未测试
        delete q;
        q = null;
    }else if(!p -> rchild){
        //右子树为空,连接其左子树
        q = p -> lchild ;
        *p = *q; //这里赋值，可能会有问题，未测试
        delete q;
        q = null;
    }else{
        //左右子树均不为空,采取用其前驱替换p
        q = p;
        s = q->lchild;
        while(s->rchild){
           q = s;
           s = s->rchild;
        }
        p->data = s -> data; //用其前驱取代p
        if(q==p){
            p->lchild = s -> lchild;            
        }else{
            q->rchild = s -> lchild;
        }
        delete s;
        s = null;
    }
}

 

 

性能分析

每个结点的为该结点的层次数。最坏情况下，当先后插入的关键字有序时，n个元素构成的二叉排序树蜕变为单支树，树的深度为，其平均查找长度为（和顺序查找相同），最好的情况是二叉排序树的形态和折半查找的判定树相同，其平均查找长度和成正比（）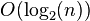

 

注：本文参考了 http://zh.wikipedia.org/wiki/%E4%BA%8C%E5%8F%89%E6%9F%A5%E6%89%BE%E6%A0%91

中的介绍，上述代码仅为说明思想，未曾测试过。