- жµПиІИ: 42475 жђ°
- жАІеИЂ:

-

жЦЗзЂ†еИЖз±ї
з§ЊеМЇзЙИеЭЧ
- жИСзЪДиµДиЃѓ ( 0)
- жИСзЪДиЃЇеЭЫ ( 0)
- жИСзЪДйЧЃз≠Ф ( 0)
е≠Шж°£еИЖз±ї
- 2015-04 ( 1)
- 2015-01 ( 1)
- 2014-12 ( 1)
- жЫіе§Ъе≠Шж°£...
жЬАжЦ∞иѓДиЃЇ
¬†¬†¬†еЕЂзЪЗеРОйЧЃйҐШпЉМжШѓдЄАдЄ™еП§иАБиАМиСЧеРНзЪДйЧЃйҐШпЉМжШѓеЫЮжЇѓзЃЧж≥ХзЪДеЕЄеЮЛдЊЛйҐШгАВиѓ•йЧЃйҐШжШѓеНБдєЭдЄЦзЇ™иСЧеРНзЪДжХ∞е≠¶еЃґйЂШжЦѓ1850еєіжПРеЗЇпЉЪеЬ®8X8ж†ЉзЪДеЫљйЩЕи±°ж£ЛдЄКжСЖжФЊеЕЂдЄ™зЪЗеРОпЉМдљњеЕґдЄНиГљдЇТзЫЄжФїеЗїпЉМеН≥дїїжДПдЄ§дЄ™зЪЗеРОйГљдЄНиГље§ДдЇОеРМдЄАи°МгАБеРМдЄАеИЧжИЦеРМдЄАжЦЬзЇњдЄКпЉМйЧЃжЬЙе§Ъе∞СзІНжСЖж≥ХгАВ¬†¬†¬†
 
import java.util.Calendar;
public class BaHuangHou {
public static int sum = 0, upperlimit = 1;
/**
*
* @param row зЇµеИЧ
* @param ld еЈ¶жЦЬзЇњ
* @param rd еП≥жЦЬзЇњ
*/
public static void compute(int row, int ld, int rd) {
//ељУrow=11111111зЪДжЧґеАЩпЉМе∞±жШѓеЕ®йГ®жЙЊеЃМдЇЖгАВ
if (row != upperlimit) {
//жЙЊеИ∞иѓ•еИЧзЪДжЙАдї•еПѓдї•жФЊзЪДдљНзљЃ
int pos = upperlimit & ~(row | ld | rd);
while (pos != 0)
{
//еПЦеЗЇзђђдЄАдЄ™еПѓдї•жФЊзЪДдљНзљЃпЉМдєЯе∞±жШѓжЬАеП≥иЊєзЪД1
int p = pos & -pos;
//еОїйЩ§еИЪеПЦеЗЇжЭ•зЪДдљНзљЃ
pos -= p;
//зїІзї≠еѓїжЙЊ,дЄ™дЄ™еПВжХ∞еє≥зІїдЄАдљН
compute(row + p, (ld + p) << 1, (rd + p) >> 1);
}
}
else sum++;//зІНжХ∞иЗ™еК†
}
public static void main(String[] args) {
Calendar start;
//иЊУеЕ•зЪЗеРОжХ∞е≠Ч
int n = 8;
//иЃЊзљЃеЉАеІЛжЧґйЧі
start = Calendar.getInstance();
//дњЭиѓБжХ∞е≠ЧеЬ®1еИ∞32дєЛйЧіпЉМйБњеЕНз≥їзїЯжЇҐеЗЇ
if ((n < 1) || (n > 32)) {
System.out.println(" еП™иГљиЃ°зЃЧ1-32дєЛйЧі\n");
return;
}
System.out.println(n + " зЪЗеРО\n");
//зїУжЭЯж†ЗењЧ uperlimti=255 иљђжНҐдЄЇдЇМињЫеИґе∞±жШѓ11111111
upperlimit = (upperlimit << n) - 1;
//дїО0пЉМ0пЉМ0еЉАеІЛ
compute(0, 0, 0);
System.out.println("еЕ±жЬЙ"
+ sum
+ "зІНжОТеИЧ, иЃ°зЃЧжЧґйЧі"
+ (Calendar.getInstance().getTimeInMillis() - start
.getTimeInMillis()) / 1000 + "зІТ \n");
}
}
 
дєНдЄАзЬЛдЉЉдєОеЃМеЕ®жСЄдЄНзЭАе§іиДСпЉМеЃЮйЩЕдЄКжХідЄ™з®ЛеЇПжШѓйЭЮеЄЄеЃєжШУзРЖиІ£зЪДгАВињЩйЗМињШжШѓеїЇиЃЃе§ІеЃґиЗ™еЈ±еНХж≠•ињРи°МдЄАжОҐз©ґзЂЯпЉМеЃЮеЬ®ж≤°з†Фз©ґеЗЇжЭ•еЖНзЬЛдЄЛйЭҐзЪДиІ£иѓігАВ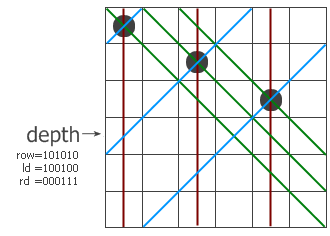 ¬†¬†
  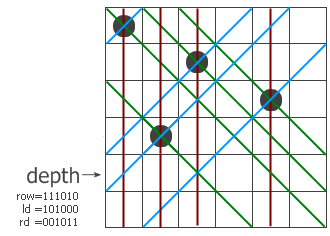
¬†¬†¬†¬†еТМжЩЃйАЪзЃЧж≥ХдЄАж†ЈпЉМињЩжШѓдЄАдЄ™йАТељТињЗз®ЛпЉМз®ЛеЇПдЄАи°МдЄАи°МеЬ∞еѓїжЙЊеПѓдї•жФЊзЪЗеРОзЪДеЬ∞жЦєгАВињЗз®ЛеЄ¶дЄЙдЄ™еПВжХ∞пЉМrowгАБldеТМrdпЉМеИЖеИЂи°®з§ЇеЬ®зЇµеИЧеТМдЄ§дЄ™еѓєиІТзЇњжЦєеРСзЪДйЩРеИґжЭ°дїґдЄЛињЩдЄАи°МзЪДеУ™дЇЫеЬ∞жЦєдЄНиГљжФЊгАВжИСдїђдї•6x6зЪДж£ЛзЫШдЄЇдЊЛпЉМзЬЛзЬЛз®ЛеЇПжШѓжАОдєИеЈ•дљЬзЪДгАВеБЗиЃЊзО∞еЬ®еЈ≤зїПйАТељТеИ∞зђђеЫЫе±ВпЉМеЙНдЄЙе±ВжФЊзЪДе≠РеЈ≤зїПж†ЗеЬ®еЈ¶еЫЊдЄКдЇЖгАВзЇҐиЙ≤гАБиУЭиЙ≤еТМзїњиЙ≤зЪДзЇњеИЖеИЂи°®з§ЇдЄЙдЄ™жЦєеРСдЄКжЬЙеЖ≤з™БзЪДдљНзљЃпЉМдљНдЇОиѓ•и°МдЄКзЪДеЖ≤з™БдљНзљЃе∞±зФ®rowгАБldеТМrdдЄ≠зЪД1жЭ•и°®з§ЇгАВжККеЃГдїђдЄЙдЄ™еєґиµЈжЭ•пЉМеЊЧеИ∞иѓ•и°МжЙАжЬЙзЪДз¶БдљНпЉМеПЦеПНеРОе∞±еЊЧеИ∞жЙАжЬЙеПѓдї•жФЊзЪДдљНзљЃпЉИзФ®posжЭ•и°®з§ЇпЉЙгАВp=p = pos & -pos;еЕґзїУжЮЬжШѓеПЦеЗЇжЬАеП≥иЊєзЪДйВ£дЄ™1гАВињЩж†ЈпЉМpе∞±и°®з§Їиѓ•и°МзЪДжЯРдЄ™еПѓдї•жФЊе≠РзЪДдљНзљЃпЉМжККеЃГдїОposдЄ≠зІїйЩ§еєґйАТељТи∞ГзФ®computeињЗз®ЛгАВж≥®жДПйАТељТи∞ГзФ®жЧґдЄЙдЄ™еПВжХ∞зЪДеПШеМЦпЉМжѓПдЄ™еПВжХ∞йГљеК†дЄКдЇЖдЄАдЄ™з¶БдљНпЉМдљЖдЄ§дЄ™еѓєиІТзЇњжЦєеРСзЪДз¶БдљНеѓєдЄЛдЄАи°МзЪДељ±еУНйЬАи¶Беє≥зІїдЄАдљНгАВжЬАеРОпЉМе¶ВжЮЬйАТељТеИ∞жЯРдЄ™жЧґеАЩеПСзО∞row=111111дЇЖпЉМиѓіжШОеЕ≠дЄ™зЪЗеРОеЕ®жФЊињЫеОїдЇЖпЉМж≠§жЧґз®ЛеЇПдїОзђђ1и°МиЈ≥еИ∞зђђ11и°МпЉМжЙЊеИ∞зЪДиІ£зЪДдЄ™жХ∞еК†дЄАгАВ
 
 
- 2012-01-12 18:38
- жµПиІИ 1272
- иѓДиЃЇ(0)
- еИЖз±ї:зЉЦз®Лиѓ≠и®А
- жЯ•зЬЛжЫіе§Ъ
еПСи°®иѓДиЃЇ
-
2012-03-16 20:52 жЬАе§ІеЕђзЇ¶жХ∞пЉЫжЬАе∞ПеЕђеАНжХ∞
2012-05-18 21:45 1391ж±ВжЬАе∞ПеЕђеАНжХ∞жЦєж≥Хе¶ВдЄЛпЉЪ (1)гАБдЄ§жХ∞зЫЄдєШж≥ХгАВ ¬†¬†¬†¬†¬†¬† ... -
и£іж≥ҐйВ£е•СзЃЧж≥Х
2012-05-18 21:40 924и£іж≥ҐйВ£е•СзЃЧж≥ХпЉМжХ∞зїДзЃЧж≥Х #include<st ... -
дЄАдЇЫзЪДзЃЧж≥ХзЪДж†ЉеЉП
2012-05-17 12:15 1095еБЪйҐШзЫЃеБЪдєЕдЇЖдєЛеРОе∞±дЉЪеПСзО∞пЉМзЃЧж≥ХжШѓжЬЙж†ЉеЉПзЪДгАВ ¬† дЄАгАБжЈ±еЇ¶дЉШ ... -
зђђдЄЙе±КиУЭж°•жЭѓйҐДиµЫзЬЯйҐШ-C++жЬђзІСзїД-10йҐШпЉИJavaеЃЮзО∞пЉЙ
2012-05-15 11:11 991¬† ¬†¬†¬† дїКзЫТе≠РйЗМжЬЙnдЄ™е∞ПзРГпЉМAгАБBдЄ§дЇЇиљЃжµБдїОзЫТдЄ≠еПЦзРГпЉМжѓПдЄ™ ... -
зђђдЄЙе±КиУЭж°•жЭѓйҐДиµЫзЬЯйҐШ-C++йЂШиБМзїД-10йҐШпЉИJavaеЃЮзО∞пЉЙ
2012-05-15 10:57 1300¬†¬†¬† 2x3=6дЄ™жЦєж†ЉдЄ≠жФЊеЕ•ABCDEдЇФдЄ™е≠ЧжѓНпЉМеП≥дЄЛиІТзЪДйВ£дЄ™ ... -
зђђдЄЙе±КиУЭж°•жЭѓйҐДиµЫзЬЯйҐШ-JavaйЂШиБМзїД-10йҐШ
2012-05-14 13:16 2012еМ™и≠¶иѓЈжЛ®110,еН≥дљњжЙЛжЬЇжђ† ... -
зђђдЄЙе±КиУЭж°•жЭѓйҐДиµЫзЬЯйҐШ-JavaжЬђзІСзїД-10йҐШ
2012-05-14 12:41 1548¬†¬†¬†¬† ж≥КжЭЊжШѓж≥ХеЫљжХ∞е≠¶еЃґгАБзЙ©зРЖе≠¶еЃґеТМеКЫе≠¶еЃґгАВдїЦдЄАзФЯиЗіеКЫзІСе≠¶дЇЛ ... -
иЃ°зЃЧ24зВє-еИ©зФ®дЇМеПЙж†СеОЯзРЖ
2012-01-10 21:03 1674йЧЃйҐШжППињ∞80еєідї£еЕ®дЄЦзХМжµБи°МдЄАзІНжХ∞е≠ЧжЄЄжИПпЉМеЬ®дЄ≠еЫљжИСдїђжККињЩзІНжЄЄжИПзІ∞ ... -
еРЄи°АйђЉжХ∞е≠Ч
2012-01-09 20:32 953йҐШзЫЃпЉЪ еРЄи°АйђЉжХ∞е≠ЧжШѓжМ ... -
е≠Чзђ¶дЄ≤зЪДжОТеИЧпЉИAпЉИm,nпЉЙпЉЙпЉМеПѓйЗНе§НйАЙ
2012-01-09 13:28 1331йҐШзЫЃпЉЪзО∞жЬЙABCDE 5дЄ™зРГ жЮДжИРзЪДжОТеИЧзїДеРИ еПѓйЗНе§НжКљеПЦ жЬАе§Ъ ... -
иЫЗ嚥зЯ©йШµ
2012-01-09 13:38 1086ProblemиЫЗ嚥зЯ©йШµжШѓзФ±1еЉАеІЛзЪДиЗ™зДґжХ∞дЊЭжђ°жОТеИЧжИРзЪДдЄАдЄ™зЯ©йШµдЄК ... -
еѓїжЙЊжЬАзЯ≠иЈѓеЊД
2012-01-07 18:51 1188йҐШзЫЃпЉЪзїЩеЃЪдЄАдЄ™иµЈзВєеТМдЄАдЄ™зїИзВєгАВеЬ®дЄАдЄ™8*8зЪДж£ЛзЫШдЄКжЙЊеЗЇдЄАжЭ°жЬАзЯ≠ ... -
е≠Чзђ¶дЄ≤зЪДжОТеИЧпЉИAпЉИm,nпЉЙпЉЙ
2012-01-07 18:18 1007йҐШзЫЃпЉЪжЬЙA,B,C,D,E 5дЄ™е≠ЧжѓНпЉМдїОеЕґдЄ≠дїїйАЙ3дЄ™пЉМи¶Бж±ВеИЧеЗЇ ... -
е≠Чзђ¶дЄ≤зЪДзїДеРИпЉИCпЉИm,nпЉЙпЉЙ
2012-01-07 17:46 1424йҐШзЫЃпЉЪжЬЙA,B,C,D,E 5дЄ™е≠ЧжѓНпЉМдїОеЕґдЄ≠дїїйАЙ3дЄ™пЉМи¶Бж±ВеИЧеЗЇ ... -
ж±ЙиѓЇе°Ф
2012-01-07 17:32 985еЕ≥дЇОж±ЙиѓЇе°Фе§ІеЃґеЇФиѓ•еЊИзЖЯжВЙеРІгАВ ¬†¬†¬† ж≤≥еЕІдєЛе°Ф(Towers ... -
дЄЙиІТиЮЇжЧЛзЯ©йШµ
2012-01-07 17:27 1148жЙУеН∞е¶ВдЄЛзЯ©йШµпЉМе¶ВжЮЬ n=7 еИЩиЊУеЗЇпЉЪ 1¬† 18 2 ...








зЫЄеЕ≥жО®иНР
жАїзЪДжЭ•иѓіпЉМињЩдЄЙдїљJavaдї£з†БдЄЇжИСдїђжПРдЊЫдЇЖе≠¶дє†еТМзРЖиІ£еЕЂзЪЗеРОйЧЃйҐШзЪДдЄНеРМиІТеЇ¶пЉМеМЕжЛђеЫЮжЇѓж≥ХгАБдљНињРзЃЧдї•еПКеПѓиГљзЪДдЉШеМЦжКАеЈІгАВйАЪињЗйШЕиѓїеТМеИЖжЮРињЩдЇЫдї£з†БпЉМжИСдїђеПѓдї•жЈ±еЕ•зРЖиІ£е¶ВдљХзФ®зЉЦз®Лиѓ≠и®АиІ£еЖ≥еЃЮйЩЕйЧЃйҐШпЉМеРМжЧґжПРеНЗжИСдїђзЪДзЃЧж≥ХиЃЊиЃ°еТМ...
еЕЂзЪЗеРОиѓЊз®ЛиЃЊиЃ° жЇРз®ЛеЇП жµБз®Ли°® ињРзЃЧзїУжЮЬ еЕЂзЪЗеРОиѓЊз®ЛиЃЊиЃ° жЇРз®ЛеЇП жµБз®Ли°® ињРзЃЧзїУжЮЬ
жЬђиµДжЇРдљњзФ®c++дї£з†БеЃЮзО∞N-зЪЗеРОйЧЃйҐШеєґйЩДдЄКз†Фз©ґе∞ПиЃЇжЦЗпЉМеЃЮзО∞зЃЧж≥ХжЬЙпЉЪеЫЮжЇѓж≥Х(йАТељТ)пЉМеЫЮжЇѓж≥Х(йАТељТ)зЪДйХЬеГПдЉШеМЦпЉМеЫЮжЇѓж≥Х(йЭЮйАТељТ)пЉМеЫЮжЇѓж≥Х(йЭЮ...N-зЪЗеРОйЧЃйҐШжШѓеЕЂзЪЗеРОйЧЃйҐШзЪДжЛУе±ХпЉМи¶БиІ£еЖ≥еЕЂзЪЗеРОйЧЃйҐШеП™йЬАи¶Бе∞ЖиЊУеЕ•зЪДеАЉиµЛдЄЇ8еН≥еПѓгАВ
ж†єжНЃзїЩеЃЪжЦЗдїґзЪДдњ°жБѓпЉМжЬђжЦЗе∞ЖеЫізїХвАЬзФ®ж±ЗзЉЦиѓ≠и®АзЉЦеЖЩеЕЂзЪЗеРОйЧЃйҐШеєґе∞ЖзїУжЮЬжШЊз§ЇеЬ®е±ПеєХдЄКвАЭзЪДдЄїйҐШињЫи°Миѓ¶зїЖиІ£жЮРгАВй¶ЦеЕИпЉМжИСдїђйЬАи¶БдЇЖиІ£еЕЂзЪЗеРОйЧЃйҐШзЪДеЯЇжЬђж¶ВењµеПКеЕґиІ£еЖ≥жАЭиЈѓпЉМйЪПеРОжЈ±еЕ•жОҐиЃ®ж±ЗзЉЦиѓ≠и®АеЃЮзО∞зЪДеЕЈдљУзїЖиКВгАВ ### еЕЂзЪЗеРО...
еЬ®8086ж±ЗзЉЦиѓ≠и®АдЄ≠пЉМеЃЮзО∞еЕЂзЪЗеРОйЧЃйҐШзЪДеی嚥иЊУеЗЇжШѓдЄАй°єжМСжИШпЉМеЫ†дЄЇеЃГжґЙеПКеИ∞е±ПеєХжШЊз§ЇгАБеЖЕе≠ШзЃ°зРЖеТМзЃЧж≥ХиЃЊиЃ°з≠Йе§ЪдЄ™жЦєйЭҐгАВ"8086ж±ЗзЉЦеЕЂзЪЗеРОеی嚥иЊУеЗЇиНЙз®њ"жШѓдЄАдЄ™й°єзЫЃпЉМеЕґзЫЃж†ЗжШѓеЬ®640x480еИЖиЊ®зОЗдЄФжФѓжМБ16иЙ≤зЪДжШЊз§ЇеЩ®дЄКдї•еی嚥жЦєеЉП...
еЬ®еЕЂзЪЗеРОйЧЃйҐШдЄ≠пЉМеПѓдї•дљњзФ®дљНжУНдљЬжЭ•и°®з§Їж£ЛзЫШзЪДзКґжАБпЉМжѓПдЄ™зЪЗеРОзЪДдљНзљЃеѓєеЇФдЄАдЄ™дЇМињЫеИґдљНпЉМе¶Взђђiи°МзЪЗеРОдљНзљЃеПѓдї•зФ®2^(i-1)и°®з§ЇпЉМйАЪињЗжМЙдљНдЄОгАБжМЙдљНжИЦз≠ЙжУНдљЬеПѓдї•ењЂйАЯж£АжЯ•жЯРи°МгАБжЯРеИЧжИЦеѓєиІТзЇњжШѓеР¶еЈ≤жЬЙзЪЗеРОгАВ 2. **жХ∞зїДеТМзЯ©йШµ*...
еЬ®еЃЮйЩЕдї£з†БдЄ≠пЉМеПѓиГљдЉЪжЬЙйҐЭе§ЦзЪДдЉШеМЦжО™жЦљпЉМе¶ВдљњзФ®дљНињРзЃЧжЭ•йЂШжХИеЬ∞ж£АжЯ•еТМиЃЊзљЃж£ЛзЫШзКґжАБпЉМжИЦиАЕдљњзФ®ж†ЗењЧжЭ•иЈЯиЄ™еЈ≤е∞ЭиѓХињЗзЪДдљНзљЃпЉМдї•еЗПе∞СдЄНењЕи¶БзЪДиЃ°зЃЧгАВ жАїдєЛпЉМињЩдЄ™еОЛзЉ©еМЕжПРдЊЫдЇЖдљњзФ®дЄ§зІНдЄНеРМжРЬ糥з≠ЦзХ•иІ£еЖ≥еЕЂзЪЗеРОйЧЃйҐШзЪДJavaеЃЮзО∞...
ињЩдЄ™з®ЛеЇПжШѓзФ®дЇОиІ£еЖ≥еЕЂзЪЗеРОйЧЃйҐШзЪДгАВеЕЂзЪЗеРОйЧЃйҐШз≠ЙдЇОи¶Бж±ВеЕЂдЄ™зЪЗеРОдЄ≠зЪДдїїжДПдЄ§дЄ™дЄНиÚ襀жФЊеЬ®еРМдЄАи°МжИЦеРМдЄАеИЧжИЦеРМдЄАжЦЬзЇњдЄКгАВеБЪињЩдЄ™иѓЊйҐШпЉМйЗНи¶БзЪДе∞±жШѓеЕИжРЮжЄЕж•ЪеУ™дЄ™дљНзљЃжШѓеРИж≥ХзЪДжФЊзЪЗеРОзЪДдљНзљЃпЉМеУ™дЄ™дЄНиГљпЉМи¶БеЕИеИ§жЦ≠пЉМеРОжФЊзљЃгАВжИСзЪД...
гАКNзЪЗеРОйЧЃйҐШдЄОеЕЂзЪЗеРОйЧЃйҐШзЪДC++еЃЮзО∞гАЛ NзЪЗеРОйЧЃйҐШеТМеЕЂзЪЗеРОйЧЃйҐШжШѓиЃ°зЃЧжЬЇзІСе≠¶йҐЖеЯЯзїПеЕЄзЪДеЫЮжЇѓзЃЧж≥ХеЃЮдЊЛпЉМеЕґдЄїи¶БзЫЃж†ЗжШѓеЬ®дЄАдЄ™N√ЧNзЪДж£ЛзЫШдЄКжФЊзљЃNдЄ™зЪЗеРОпЉМдљњеЊЧдїїжДПдЄ§дЄ™зЪЗеРОйГљжЧ†ж≥ХеЬ®еРМдЄАи°МгАБеРМдЄАеИЧжИЦеРМдЄАеѓєиІТзЇњдЄКзЫЄдЇТжФїеЗїгАВињЩ...
еЕЂзЪЗеРОйЧЃйҐШжШѓдЄАдЄ™зїПеЕЄзЪДйЧЃйҐШпЉМеЬ®ж£ЛзЫШдЄКжФЊзљЃеЕЂдЄ™зЪЗеРОпЉМдљњеЕґдЄНиГљдЇТзЫЄжФїеЗїпЉМеН≥дїїжДПдЄ§дЄ™зЪЗеРОйГљдЄНиГље§ДдЇОеРМдЄАи°МгАБеРМдЄАеИЧжИЦеРМдЄАеѓєиІТзЇњдЄКгАВињЩдЄ™йЧЃйҐШеЬ®иЃ°зЃЧжЬЇзІСе≠¶дЄ≠媪襀зФ®жЭ•жХЩжОИеЫЮжЇѓж≥ХеТМйАТељТжАЭжГ≥гАВеЬ®ињЩдЄ™еЃЮзО∞дЄ≠пЉМжИСдїђдЄНдїЕиІ£еЖ≥...
еЬ®иЃ°зЃЧжЬЇзІСе≠¶еТМжХ∞е≠¶йҐЖеЯЯдЄ≠пЉМеЕЂзЪЗеРОйЧЃйҐШжШѓдЄАй°єзїПеЕЄзЪДзЃЧж≥ХйЧЃйҐШпЉМеЃГдЄНдїЕжШѓжХ∞жНЃзїУжЮДиѓЊз®ЛиЃЊиЃ°дЄ≠зЪДдЄАдЄ™зїПеЕЄй°єзЫЃпЉМдєЯжШѓиЃ≠зїГзЃЧж≥ХиЃЊиЃ°еТМзЉЦз®ЛеЃЮиЈµиГљеКЫзЪДжЬЙжХИйАФеЊДгАВиѓ•йЧЃйҐШи¶Бж±ВеЬ®8x8зЪДж£ЛзЫШдЄКжФЊзљЃ8дЄ™зЪЗеРОпЉМдљњеЊЧеЃГдїђдЇТдЄНжФїеЗїпЉМеН≥...
ж†ЗйҐШдЄ≠зЪДвАЬbahuanghou.rar_ж†ИеЕЂзЪЗеРОвАЭжЪЧз§ЇдЇЖињЩжШѓдЄАдЄ™еЕ≥дЇОиІ£еЖ≥еЕЂзЪЗеРОйЧЃйҐШзЪДз®ЛеЇПпЉМдљњзФ®дЇЖж†ИдљЬдЄЇжХ∞жНЃзїУжЮДпЉМзЉЦз®Лиѓ≠и®АдЄЇCгАВеЕЂзЪЗеРОйЧЃйҐШжШѓзїПеЕЄзЪДиЃ°зЃЧжЬЇзЃЧж≥ХйЧЃйҐШпЉМзЫЃж†ЗжШѓеЬ®дЄАдЄ™8x8зЪДж£ЛзЫШдЄКжФЊзљЃеЕЂдЄ™зЪЗеРОпЉМдљњеЊЧдїїдљХдЄ§дЄ™зЪЗеРОйГљ...
ињЩйЬАи¶БеИ©зФ®еЫЮжЇѓгАБйАТељТз≠ЙжЦєж≥ХжЭ•е∞ЭиѓХжЙАжЬЙеПѓиГљзЪДжФЊзљЃжЦєж°ИпЉМеєґйАЪињЗдљНињРзЃЧжИЦиАЕжХ∞зїДжЭ•ж†ЗиЃ∞еЈ≤жФЊзљЃзЪДзЪЗеРОдљНзљЃпЉМйБњеЕНеЖ≤з™БгАВж≠§йЧЃйҐШиГљйФїзВЉеѓєеЖ≤з™Бж£АжµЛеТМиІ£еЖ≥жЦєж°ИдЉШеМЦзЪДиГљеКЫпЉМжШѓе≠¶дє†зЃЧж≥ХеТМжХ∞жНЃзїУжЮДзЪДе•љдЊЛе≠РгАВ еЬ®иѓЊз®ЛиЃЊиЃ°дЄ≠пЉМињЩдЇЫ...
жАїзЪДжЭ•иѓіпЉМиІ£еЖ≥еЕЂзЪЗеРОйЧЃйҐШйЬАи¶БзРЖиІ£еєґињРзФ®еЫЮжЇѓж≥ХгАБйАТељТгАБжХ∞зїДпЉИжИЦдљНињРзЃЧпЉЙи°®з§Їдї•еПКйЧЃйҐШзЪДзЇ¶жЭЯжЭ°дїґгАВйАЪињЗињЩдЄ™йҐШзЫЃпЉМз®ЛеЇПеСШеПѓдї•йФїзВЉйАїиЊСжАЭзїіиГљеКЫпЉМе≠¶дє†е¶ВдљХе§ДзРЖе§НжЭВйЧЃйҐШзЪДж±ВиІ£з≠ЦзХ•гАВеЬ®еИЖжЮРжПРдЊЫзЪДеОЛзЉ©еМЕжЦЗдїґ...
еЬ®иЃ°зЃЧжЬЇзІСе≠¶йҐЖеЯЯпЉМеЕЂзЪЗеРОйЧЃйҐШжШѓдЄАдЄ™зїПеЕЄзЪДйЧЃйҐШпЉМеЃГжґЙеПКеИ∞зЃЧж≥ХиЃЊиЃ°гАБеЫЮжЇѓж≥Хдї•еПКдљНињРзЃЧз≠Йж†ЄењГж¶ВењµгАВиѓ•йЧЃйҐШзФ±19дЄЦзЇ™зЪДжХ∞е≠¶еЃґеЉЧйЗМеЊЈйЗМеЄМ¬ЈйЂШжЦѓжПРеЗЇпЉМи¶Бж±ВеЬ®8√Ч8зЪДж£ЛзЫШдЄКжСЖжФЊ8дЄ™зЪЗеРОпЉМдљњеЊЧдїїжДПдЄ§дЄ™зЪЗеРОйГљдЄНиГљеЬ®еРМдЄАи°МгАБ...
- дЄЇдЇЖйБњеЕНйЗНе§НиЃ°зЃЧпЉМеПѓдї•дљњзФ®дљНињРзЃЧжЭ•ж†ЗиЃ∞еИЧеТМеѓєиІТзЇњзЪДзКґжАБпЉМжПРйЂШжХИзОЗгАВ - дљњзФ®жЈ±еЇ¶дЉШеЕИжРЬ糥пЉИDFSпЉЙињЫи°МеЫЮжЇѓпЉМеЫ†дЄЇеЕЂзЪЗеРОйЧЃйҐШзЪДиІ£жХ∞йЗПзЫЄеѓєиЊГе∞СпЉМDFSйАЪеЄЄиґ≥е§ЯйЂШжХИгАВ 7. **еЃЮйЩЕеЇФзФ®**пЉЪ - еЕЂзЪЗеРОйЧЃйҐШзЪДиІ£еЖ≥жАЭиЈѓ...
### еЕЂзЪЗеРОйЧЃйҐШж±ВиІ£вАФвАФдєЛйАТељТ #### дЄАгАБеЕЂзЪЗеРОйЧЃйҐШж¶Вињ∞ еЕЂзЪЗеРОйЧЃйҐШжШѓзФ±еЫљйЩЕи•њжіЛж£Лж£ЛжЙЛй©ђеЕЛжЦѓ¬ЈиіЭзСЯе∞ФеЬ®1848еєіжПРеЗЇзЪДзїПеЕЄйЧЃйҐШгАВињЩдЄ™йЧЃйҐШи¶Бж±ВеЬ®8√Ч8зЪДеЫљйЩЕи±°ж£Лж£ЛзЫШдЄКжФЊзљЃеЕЂдЄ™зЪЗеРОпЉМдљњеЊЧдїїжДПдЄ§дЄ™зЪЗеРОдєЛйЧійГљдЄНиГљзЫЄдЇТ...
жАїзЪДжЭ•иѓіпЉМеЕЂзЪЗеРОйЧЃйҐШзЪДж±ВиІ£жШѓеѓєжХ∞жНЃзїУжЮДеТМзЃЧж≥ХзЪДеЃЮиЈµињРзФ®пЉМеЃГжґµзЫЦдЇЖеЫЮжЇѓж≥ХгАБйАТељТгАБдљНињРзЃЧдї•еПКеЯЇз°АзЪДзФ®жИЈдЇ§дЇТиЃЊиЃ°гАВињЩдЄ™иѓЊз®ЛиЃЊиЃ°жЬЙеК©дЇОжПРеНЗе≠¶зФЯзЪДйАїиЊСжАЭзїіиГљеКЫеТМзЉЦз®ЛжКАеЈІпЉМеРМжЧґдєЯжШѓеѓєзїПеЕЄйЧЃйҐШзЪДзО∞дї£иЃ°зЃЧжЬЇзІСе≠¶иІ£з≠ФгАВ