转:http://highlyscalable.wordpress.com/2012/06/05/fast-intersection-sorted-lists-sse/
Intersection of sorted lists is a cornerstone operation in many applications including search engines and databases because indexes are often implemented using different types of sorted structures. At GridDynamics, we recently worked on a custom database for realtime web analytics where fast intersection of very large lists of IDs was a must for good performance. From a functional point of view, we needed mainly a standard boolean query processing, so it was possible to use Solr/Lucene as a platform. However, it was interesting to evaluate performance of alternative approaches. In this article I describe several useful techniques that are based on SSE instructions and provide results of performance testing for Lucene, Java, and C implementations. I’d like to mention that in this study we were focused on a general case when selectivity of the intersection is low or unknown and optimization techniques like skip list are not necessarily beneficial.
Scalar Intersection
Our starting point is a simple element-by-element intersection algorithm (also known as Zipper). Its implementation in C is shown below and do not require lengthy explanations:
01 |
#define int32 unsigned int |
07 |
size_t intersect_scalar(int32 *A, int32 *B, size_t s_a, size_t s_b, int32 *C) {
|
08 |
size_t i_a = 0, i_b = 0;
|
11 |
while(i_a < s_a && i_b < s_b) {
|
14 |
} else if(B[i_b] < A[i_a]) {
|
17 |
C[counter++] = A[i_a];
|
Performance of this procedure both in C and Java will be evaluated in the last section. I believe that it is possible to improve this approach using a branchless implementation, but I had no chance to try it out.
Vectorized Intersection
It is intuitively clear that performance of intersection may be improved by processing of multiple elements at once using SIMD instructions. Let us start with the following question: how to find and extract common elements in two short sorted arrays (let’s call them segments). SSE instruction set allow one to do a pairwise comparison of two segments of four 32-bit integers each using one instruction (_mm_cmpeq intrinsic) that produces a bit mask that highlights positions of equal elements. If one has two 4-element registers, A and B, it is possible to obtain a mask of common elements comparing A with different cyclic shifts of B (the left part of the figure below) and OR-ing the masks produced by each comparison (the right part of the figure):
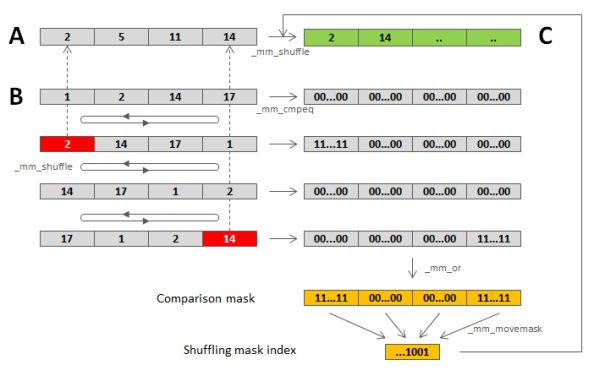
The resulting comparison mask highlights the required elements in the segment A. This 128-bit mask can be transformed to a 4-bit value (shuffling mask index) using __mm_movemask intrinsic. When this short mask of common elements is obtained, we have to efficiently copy out common elements. This can be done by shuffling of the original elements according to the shuffling mask that can be looked up in the precomputed dictionary using the shuffling mask index (i.e. each of 16 possible 4-bit shuffling mask indexes is mapped to some permutation). All common elements should be placed to the beginning of the register, in this case register can be copied in one shot to the output buffer C as it shown in the figure above.
The described technique gives us a building block that can be used for intersection of long sorted lists. This process is somehow similar to the scalar intersection:
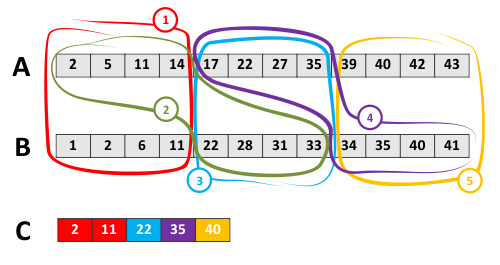
In this example, during the first cycle we compare first 4-element segments (highlighted in red) and copy out common elements (2 and 11). Similarly to the scalar intersection algorithm, we can move forward the pointer for the list B because the tail element of the compared segments is smaller in B (11 vs 14). At the second cycle (in green) we compare the first segment of A with the second segment of B, intersection is empty, and we move pointer for A. And so on. In this example, we need 5 comparisons to process two lists of 12 elements each.
The complete implementation of the described techniques is shown below:
01 |
static __m128i shuffle_mask[16];
|
03 |
size_t intersect_vector(int32 *A, int32 *B, size_t s_a, size_t s_b, int32 *C) {
|
05 |
size_t i_a = 0, i_b = 0;
|
08 |
size_t st_a = (s_a / 4) * 4;
|
09 |
size_t st_b = (s_b / 4) * 4;
|
11 |
while(i_a < s_a && i_b < s_b) {
|
13 |
__m128i v_a = _mm_load_si128((__m128i*)&A[i_a]);
|
14 |
__m128i v_b = _mm_load_si128((__m128i*)&B[i_b]);
|
18 |
int32 a_max = _mm_extract_epi32(v_a, 3);
|
19 |
int32 b_max = _mm_extract_epi32(v_b, 3);
|
20 |
i_a += (a_max <= b_max) * 4;
|
21 |
i_b += (a_max >= b_max) * 4;
|
25 |
int32 cyclic_shift = _MM_SHUFFLE(0,3,2,1);
|
26 |
__m128i cmp_mask1 = _mm_cmpeq_epi32(v_a, v_b);
|
27 |
v_b = _mm_shuffle_epi32(v_b, cyclic_shift);
|
28 |
__m128i cmp_mask2 = _mm_cmpeq_epi32(v_a, v_b);
|
29 |
v_b = _mm_shuffle_epi32(v_b, cyclic_shift);
|
30 |
__m128i cmp_mask3 = _mm_cmpeq_epi32(v_a, v_b);
|
31 |
v_b = _mm_shuffle_epi32(v_b, cyclic_shift);
|
32 |
__m128i cmp_mask4 = _mm_cmpeq_epi32(v_a, v_b);
|
33 |
__m128i cmp_mask = _mm_or_si128(
|
34 |
_mm_or_si128(cmp_mask1, cmp_mask2),
|
35 |
_mm_or_si128(cmp_mask3, cmp_mask4)
|
38 |
int32 mask = _mm_movemask_ps((__m128)cmp_mask);
|
42 |
__m128i p = _mm_shuffle_epi8(v_a, shuffle_mask[mask]);
|
43 |
_mm_storeu_si128((__m128i*)&C[count], p);
|
44 |
count += _mm_popcnt_u32(mask);
|
The described implementation uses the shuffle_mask dictionary to map the mask of common elements to the shuffling parameter. Building of this dictionary is straightforward (each bit in the mask corresponds to 4 bytes in the register):
02 |
void prepare_shuffling_dictionary() {
|
03 |
for(int i = 0; i < 16; i++) {
|
06 |
memset(permutation, 0xFF, sizeof(permutation));
|
07 |
for(char b = 0; b < 4; b++) {
|
09 |
permutation[counter++] = 4*b;
|
10 |
permutation[counter++] = 4*b + 1;
|
11 |
permutation[counter++] = 4*b + 2;
|
12 |
permutation[counter++] = 4*b + 3;
|
15 |
__m128i mask = _mm_loadu_si128((const __m128i*)permutation);
|
16 |
shuffle_mask[i] = mask;
|
20 |
int getBit(int value, int position) {
|
21 |
return ( ( value & (1 << position) ) >> position);
|
Partitioned Vectorized Intersection
SSE 4.2 instruction set offers PCMPESTRM instruction that allows one to compare two segments of eight 16-bit values each and obtain a bit mask that highlights common elements. This sounds like an extremely efficient approach for intersection of sorted lists, but in its basic form this approach is limited by 16-bit values in the lists. This is not the case for many applications, so a workaround was recently suggested by Benjamin Schedel et al. in this article. The main idea is to store indexes in the partitioned format, where elements with the same most significant bits are grouped together. This approach also has limited applicability because each partition should contain a sufficient number of elements, i.e. it works well in case or very large lists or favorable distribution of the values.
Each partition has a header that includes a prefix which represents most significant bits that are common for all elements in the partition and the number of elements in the partition. The following figure illustrates the partitioning process:
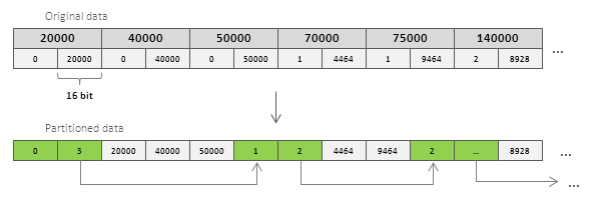
The partitioning procedure that coverts 32-bit values into 16-bit values is shown in the code snippet below:
04 |
size_t partition(int32 *A, size_t s_a, int16 *R) {
|
06 |
size_t partition_length = 0;
|
07 |
size_t partition_size_position = 1;
|
09 |
for(size_t p = 0; p < s_a; p++) {
|
10 |
int16 chigh = _high16(A[p]);
|
11 |
int16 clow = _low16(A[p]);
|
12 |
if(chigh == high && p != 0) {
|
19 |
R[partition_size_position] = partition_length;
|
21 |
partition_size_position = counter - 2;
|
25 |
R[partition_size_position] = partition_length;
|
A pair of partitions can be intersected using the following procedure that computes a mask of common elements using _mm_cmpestrm intrinsic and then shuffles these elements similarly to the vectorized intersection procedure what was described in the previous section.
01 |
size_t intersect_vector16(int16 *A, int16 *B, size_t s_a, size_t s_b, int16 *C) {
|
03 |
size_t i_a = 0, i_b = 0;
|
05 |
size_t st_a = (s_a / 8) * 8;
|
06 |
size_t st_b = (s_b / 8) * 8;
|
08 |
while(i_a < st_a && i_b < st_b) {
|
09 |
__m128i v_a = _mm_loadu_si128((__m128i*)&A[i_a]);
|
10 |
__m128i v_b = _mm_loadu_si128((__m128i*)&B[i_b]);
|
12 |
__m128i res_v = _mm_cmpestrm(v_b, 8, v_a, 8,
|
13 |
_SIDD_UWORD_OPS|_SIDD_CMP_EQUAL_ANY|_SIDD_BIT_MASK);
|
14 |
int r = _mm_extract_epi32(res_v, 0);
|
15 |
__m128i p = _mm_shuffle_epi8(v_a, shuffle_mask16[r]);
|
16 |
_mm_storeu_si128((__m128i*)&C[count], p);
|
17 |
count += _mm_popcnt_u32(r);
|
19 |
int16 a_max = _mm_extract_epi16(v_a, 7);
|
20 |
int16 b_max = _mm_extract_epi16(v_b, 7);
|
21 |
i_a += (a_max <= b_max) * 4;
|
22 |
i_b += (a_max >= b_max) * 4;
|
The whole intersection algorithm looks similarly to the scalar intersection. It receives two partitioned operands, iterates over headers of partitions and calls intersection of particular partitions if their prefixes match:
02 |
size_t intersect_partitioned(int16 *A, int16 *B, size_t s_a, size_t s_b, int16 *C) {
|
03 |
size_t i_a = 0, i_b = 0;
|
06 |
while(i_a < s_a && i_b < s_b) {
|
08 |
i_a += A[i_a + 1] + 2;
|
09 |
} else if(B[i_b] < A[i_a]) {
|
10 |
i_b += B[i_b + 1] + 2;
|
12 |
C[counter++] = A[i_a];
|
13 |
int16 partition_size = intersect_vector16(&A[i_a + 2], &B[i_b + 2],
|
14 |
A[i_a + 1], B[i_b + 1], &C[counter + 1]);
|
15 |
C[counter++] = partition_size;
|
16 |
counter += partition_size;
|
17 |
i_a += A[i_a + 1] + 2;
|
18 |
i_b += B[i_b + 1] + 2;
|
The output of this procedure is also a partitioned vector that can be used in further operations.
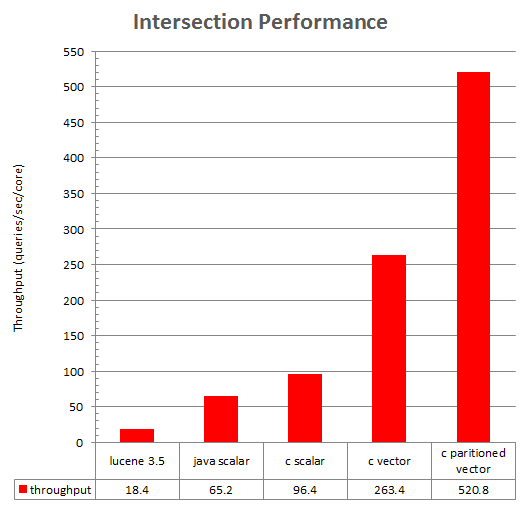
Performance Evaluation
Performance of the described techniques was evaluated for intersection of sorted lists of size 1 million elements, with average intersection selectivity about 30%. All evaluated methods excepts partitioned vectorized intersection do not require specific properties of the values in the lists. For partitioned vectorized intersection values were selected from range [0, 3M] to provide relatively large partitions.
In case of Lucene, a corpus of documents with two fields was generated to provide the mentioned index sizes and selectivity; RAMDirectory was used. Intersection was done using standard Boolean query with top hits limited by 1 to prevent generation of large result set. Of course, this not a fair comparison because Lucene is much more than a list intersector, but it is still interesting to try it out.
Performance testing was done on the ordinary Linux desktop with 2.8GHz cores. JDK 1.6 and gcc 4.5.2 (with -O3 option) were used.
分享到:
















相关推荐
Fast Sorted-Set Intersection using SIMD InstructionsBenjamin Schlegel TU DresdenDresden, Germanybenjamin.schlegel@tu- dresden.deThomas Willhalm Intel GmbHMunich, Germanythomas.willhalm@intel....
of Sorted IntegersDaniel Lemire LICEF Research CenterTELUQ, Université du Québec5800 Saint-DenisMontreal, QC H2S 3L5 Can.lemire@gmail.comLeonid Boytsov Language Technologies InstituteCarnegie ...
javascript js_leetcode题解之160-intersection-of-two-linked-lists.js
python python_leetcode题解之160_Intersection_of_Two_Linked_Lists.py
《Smarter Decisions–The Intersection of Internet of Things and Decision Science》这本书,旨在结合物联网与决策科学的优势,通过数据科学的力量,帮助读者深入理解这一交汇点,进而能在相关项目中做出更加明智...
《Fast Minimum Storage Ray Triangle Intersection》是一篇经典的计算机图形学论文,主要探讨了如何高效地进行射线与三角形网格的碰撞检测。这篇论文的核心在于提出了一种存储需求小且计算速度快的方法来确定射线与...
"Intersection Point Using C"的主题涉及到在UG环境中利用C语言编程实现查找交点的功能,这通常是进行复杂几何形状分析或零件设计时的重要步骤。 在UG OPEN环境下,开发者可以利用其提供的API(应用程序接口)来...
标题"UG Intersection Point Using C update"指的是通过UG软件的开放接口UG OPEN,利用C语言编程实现点构造器中的交点功能的更新或增强。 在UG软件中,点构造器是一种工具,它允许用户通过不同的几何对象之间的相互...
curve intersection using bezier clipping 计算多项式根的数值方法
信息安全_数据安全_Intersection of Data Breach Noti 常规渗透 可信编译 态势感知 安全审计 企业安全
两个大数组的交集
350. 两个数组的交集II Intersection of Two Arrays II思路一:排序找交集,从小到大遍历,遇到相等的就加到ans中,然后都看下一
"Intersection Point Using C new"这个标题指的是通过UG的开放接口(UG Open)利用C++编程语言实现交点构造的功能,类似于UG软件内置的Point Constructor工具。 在UG软件中,Point Constructor是一个用于创建点对象...
### 参数曲面与平面相交算法 #### 概述 在计算机图形学和几何建模领域,参数曲面与平面的相交问题是一项基础而重要的任务。由Randy B. Lee与David A....该算法通过利用基本的微分几何分析来实现高效率、低内存消耗,...
leetcode中文版 LeetCode/Cpp 本人刷题记录在此,包含题意理解与算法思路,包含在Cpp文件内部注释,后续会持续更新。 有不懂的可以联系ji648513181,同时也欢迎志同道合O的朋友一起...160.Intersection of Two Linke
### 基于GPS数据的信号交叉口延迟预测模型 #### 概述 随着城市化进程的加速和技术的发展,公共交通系统面临着越来越大的挑战。一方面,城市中的私人车辆数量不断增加,导致道路拥堵现象日益严重;...
intersection.cpp