POJ 1324 Holedox Moving 贪食蛇

Description

During winter, the most hungry and severe time, Holedox sleeps in its lair. When spring comes, Holedox wakes up, moves to the exit of its lair, comes out, and begins its new life. 
Holedox is a special snake, but its body is not very long. Its lair is like a maze and can be imagined as a rectangle with n*m squares. Each square is either a stone or a vacant place, and only vacant places allow Holedox to move in. Using ordered pair of row and column number of the lair, the square of exit located at (1,1). 

Holedox's body, whose length is L, can be represented block by block. And let B1(r1,c1) B2(r2,c2) .. BL(rL,cL) denote its L length body, where Bi is adjacent to Bi+1 in the lair for 1 <= i <=L-1, and B1 is its head, BL is its tail. 

To move in the lair, Holedox chooses an adjacent vacant square of its head, which is neither a stone nor occupied by its body. Then it moves the head into the vacant square, and at the same time, each other block of its body is moved into the square occupied by the corresponding previous block. 

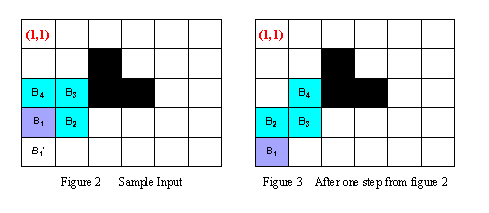
For example, in the Figure 2, at the beginning the body of Holedox can be represented as B1(4,1) B2(4,2) B3(3,2)B4(3,1). During the next step, observing that B1'(5,1) is the only square that the head can be moved into, Holedox moves its head into B1'(5,1), then moves B2 into B1, B3 into B2, and B4 into B3. Thus after one step, the body of Holedox locates in B1(5,1)B2(4,1)B3(4,2) B4(3,2) (see the Figure 3). 

Given the map of the lair and the original location of each block of Holedox's body, your task is to write a program to tell the minimal number of steps that Holedox has to take to move its head to reach the square of exit (1,1). 

Input

The input consists of several test cases. The first line of each case contains three integers n, m (1<=n, m<=20) and L (2<=L<=8), representing the number of rows in the lair, the number of columns in the lair and the body length of Holedox, respectively. The next L lines contain a pair of row and column number each, indicating the original position of each block of Holedox's body, from B1(r1,c1) to BL(rL,cL) orderly, where 1<=ri<=n, and 1<=ci<=m,1<=i<=L. The next line contains an integer K, representing the number of squares of stones in the lair. The following K lines contain a pair of row and column number each, indicating the location of each square of stone. Then a blank line follows to separate the cases. 

The input is terminated by a line with three zeros. 

Note: Bi is always adjacent to Bi+1 (1<=i<=L-1) and exit square (1,1) will never be a stone. 

Output

For each test case output one line containing the test case number followed by the minimal number of steps Holedox has to take. "-1" means no solution for that case.

Sample Input

5 6 4
4 1
4 2
3 2
3 1
3
2 3
3 3
3 4

4 4 4
2 3
1 3
1 4
2 4
4

2 1
2 2
3 4
4 2

0 0 0

Sample Output

Case 1: 9
Case 2: -1

Hint

In the above sample case, the head of Holedox can follows (4,1)->(5,1)->(5,2)->(5,3)->(4,3)->(4,2)->(4,1)->(3,1)->(2,1)->(1,1) to reach the square of exit with minimal number of step, which is nine. 

题意：给你一个n*m的矩形，然后是长度为L的贪食蛇，接下来L行是贪食蛇蛇身的坐标。

再给出K，接下来K行给出石头的坐标（不可达）。

问，贪食蛇到达坐标（1，1）的最短路径长度，不可达输出-1。

思路：显然是一道BFS，但是和以前做的又有些不同，因为以前的visit[][]是用来表示这个点是否被访问过，但是因为这条贪食蛇的蛇身也是在动的，所以这一步走过之后存在一个visit[][]数组更新的问题。

所以这里引入了visit[][][state]三维数组。前两个元素代表visit的坐标。最后一个表示当前贪食蛇的状态。

因为每一个贪食蛇的后一状态都是由前一状态通过上下左右移动来完成的。那么就可以将一整条的贪食蛇表示成一个状态数值。

这样就解决了BFS时visit[][][]数组的不同，接下来就是直接BFS了。当然这样做的结果就是TLE。

首先优化了STL队列。手写了一个队列，解决了TLE的问题。

当然由于不知道数组该开多大，这里MLE和RE了几次。最后A掉的时候

10649144

CUGB_kdq

1324

Accepted

62864K

2094MS

C++

3777B

2012-08-10 15:20:03

进一步优化，再网上看到别人的想法，就是首先只考虑蛇头，蛇身都忽略掉，这时候算出蛇头到（1，1）的最短路记为min。然后将蛇身拿出来看作不能动（即stone），再从蛇头走到（1，1）算出最短路记为max。

如果min==0，则（1，1）不可达。

如果min==max，则到达（1，1）的最短路径为min。

否则最短路径区间为[min，max]。

所以我就又写了一个BFS来求出min，max。结果是：

10650377

CUGB_kdq

1324

Accepted

47336K

735MS

G++

4910B

2012-08-10 16:53:07

速度上有了明显的加快，接下来就不会优化了。。。

 

PS:关于这个state的计算。

如左图，我们可以将state看成一个四进制的数字，B2-B1向左，B3-B2向下，B4-B3向右。每个方向代表不同的数字（根据BFS时自己定义的move数组的方向,下面代码是left,down,right,up,分别表示0，1，2，3）

可以表示成三位四进制数 210.

如右图，B2-B1向下，B3-B2向左，B4-B3向下。可以表示为 101 .

当然这个只是想法，具体操作见下面的代码。

这样的话，每个贪食蛇的形状都有一个唯一的四进制数来表示。所以state表示贪食蛇的形状是可以唯一表示的。

而visit[][][]前两个元素正好存贪食蛇的蛇头，那么这个贪食蛇在矩阵中的位置和形状就是唯一确定的。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <string>
#include <cmath>
#include <cstring>
#include <queue>
#include <set>
#include <vector>
#include <stack>
#include <map>
#include <iomanip>
#define PI acos(-1.0)
#define Max 2005
#define inf 1<<28
using namespace std;

int n,m,k;
struct snake
{
    int x,y;
} Snake[10],q1[1000000];//记录贪食蛇的坐标
int ans=-1;
struct snakeState
{
    snake body[8];
    int num;
} q[1000000];//一整条蛇和蛇走的路程
bool Map[21][21];
bool visit[21][21][17000];
int movex[4]= {0,1,0,-1}; //l,d,r,u
int movey[4]= {-1,0,1,0};
bool visit1[21][21];
int move[21][21];
int inmap(snake &x,snake body[])//判断是否可以走这步
{
    if(x.x<=0||x.y<=0||x.x>n||x.y>m||Map[x.x][x.y])
        return 0;
    for(int i=1; i<k; i++)//蛇头与蛇身相撞，则不可以走
        if(x.x==body[i].x&&x.y==body[i].y)
            return 0;
    for(int i=k-1; i>0; i--)//如果可以走这步将贪食蛇的位置更新
        body[i]=body[i-1];
    body[0].x=x.x;//贪食蛇蛇头的新坐标
    body[0].y=x.y;
    return 1;//返回成功
}
int findmove(snake &a,snake &b)//找出从位置b-a是哪个方向过来的
{
    if(a.x==b.x)
    {
        if(a.y<b.y)
            return 0;//返回值与movex,movey的值要匹配
        else return 1;
    }
    else
    {
        if(a.x>b.x)
            return 3;
        else return 2;
    }
}
void bfs()
{
    int i,j;
    snakeState a;
    for(i=0; i<k; i++)
        a.body[i]=Snake[i];
    int num=0,cnt=0;
    a.num=0;
    int state=0;
    for(i=0; i<k-1; i++)
        state=4*state+findmove(Snake[i],Snake[i+1]);//计算贪食蛇的状态（唯一性）根据前一状态走到后一状态的方向计算得出
    visit[Snake[0].x][Snake[0].y][state]=1;
    q[0]=a;
    num++;
    while(cnt<num)
    {
        snakeState temp=q[cnt];
        cnt++;
        if(temp.body[0].x==1&&temp.body[0].y==1)
        {
            ans=temp.num;
            return ;
        }
        for(i=0; i<4; i++)
        {
            snakeState now=temp;
            snake now1;
            now1.x=temp.body[0].x+movex[i];
            now1.y=temp.body[0].y+movey[i];
            if(!inmap(now1,now.body))//是否可以走
                continue;
            now.num=temp.num+1;
            state=0;
            for(j=0; j<k-1; j++)
                state=4*state+findmove(now.body[j],now.body[j+1]);//计算当前的状态
            if(visit[now.body[0].x][now.body[0].y][state])
                continue;
            visit[now.body[0].x][now.body[0].y][state]=1;
            if(now.body[0].x==1&&now.body[0].y==1)
            {
                ans=now.num;
                return ;
            }
            q[num]=now;
            num++;
        }
    }
}
void bfs1()//计算min和max
{
    int num=0,cnt=0;
    q1[num]=Snake[0];
    num++;
    visit1[Snake[0].x][Snake[0].y]=1;
    move[Snake[0].x][Snake[0].y]=1;
    while(cnt<num)
    {
        snake temp=q1[cnt];
        cnt++;
        if(temp.x==1&&temp.y==1)
        {
            return ;
        }
        for(int i=0; i<4; i++)
        {
            int tx=temp.x+movex[i];
            int ty=temp.y+movey[i];
            if(tx>=1&&ty>=1&&tx<=n&&ty<=m&&!visit1[tx][ty])
            {
                move[tx][ty]=move[temp.x][temp.y]+1;
                if(tx==1&&ty==1)
                    return ;
                visit1[tx][ty]=1;
                snake now;
                now.x=tx;
                now.y=ty;
                q1[num]=now;
                num++;
            }
        }
    }
}
void show()
{
    int i,j;
    for(i=1; i<=n; i++)
    {
        for(j=1; j<=m; j++)
            cout<<move[i][j]<<" ";
        cout<<endl;
    }

}
int main()
{
    int i,j,l,CASE=0;
    while(scanf("%d%d%d",&n,&m,&k),n|m|k)
    {
        memset(Map,0,sizeof(Map));
        memset(visit,0,sizeof(visit));
        memset(visit1,0,sizeof(visit1));
        memset(move,0,sizeof(move));
        for(i=0; i<k; i++)
        {
            scanf("%d%d",&Snake[i].x,&Snake[i].y);
        }
        int kkk,x,y;
        ans=-1;
        //show();
        scanf("%d",&kkk);
        while(kkk--)
        {
            scanf("%d%d",&x,&y);
            Map[x][y]=1;
            visit1[x][y]=1;
        }
        bfs1();//第一次BFS只考虑蛇头和stone;
        //show();
        if(move[1][1]==0)//如果（1，1）不可到达
        {
            printf("Case %d: -1\n",++CASE);
            continue;
        }
        int min=move[1][1];
        memset(move,0,sizeof(move));
        for(i=1; i<=n; i++)
        {
            for(j=1; j<=m; j++)
                visit1[i][j]=Map[i][j];
        }
        for(i=1; i<k; i++)//第二次BFS，还要另外将蛇身看成stone
            visit1[Snake[i].x][Snake[i].y]=1;
        bfs1();
        int max=move[1][1];
        if(min==max)//如果 min和max相等
        {
            printf("Case %d: %d\n",++CASE,min-1);
            continue;
        }
        bfs();
        printf("Case %d: %d\n",++CASE,ans);
    }
    return 0;
}

A完之后神清气爽啊~~