1гҖҒиғҢжҷҜе’Ңй—®йўҳ
- жҚ®з»ҹи®Ўи¶…иҝҮ80%зҡ„з”ЁжҲ·йқ жҗңзҙўеј•ж“ҺиҺ·еҸ–дҝЎжҒҜ
- зҪ‘з«ҷжҺ’еҗҚжҳҜзҪ‘з»ңжҗңзҙўеј•ж“Һзҡ„ж ёеҝғ
- зӣ®еүҚGoogleж•°жҚ®еә“еӯҳеӮЁдёҠзҷҫдәҝзҪ‘йЎөдҝЎжҒҜ, жҜҸеӨ©жҸҗдҫӣжҹҘиҜўжңҚеҠЎиҫҫеҲ°3дәҝеӨҡж¬Ў
2гҖҒgoogleжҹҘиҜўиҝҮзЁӢзӨәж„Ҹеӣҫ
3гҖҒGoogleжҗңзҙўзҡ„ж ёеҝғз®—жі•
- PageRankжҳҜ Google з”ЁдәҺиҜ„д»·дёҖдёӘзҪ‘йЎөзҡ„йҮҚиҰҒжҖ§зҡ„дёҖз§Қж–№жі•. йҖҡиҝҮиҜҘж–№жі•, Google е°Ҷеҗ„дёӘзҪ‘з«ҷиҝӣиЎҢжҺ’еҗҚ. з”ЁжҲ·иҝӣиЎҢзӣёе…іжҗңзҙўж—¶, Google дјҡе°Ҷз¬ҰеҗҲжқЎд»¶зҡ„зҪ‘з«ҷжҢүжҺ’еҗҚйЎәеәҸиҫ“еҮә.
- PageRank з®—жі•дёӯдҪҝз”Ёзҡ„ж•°еӯҰзҹҘиҜҶеҢ…жӢ¬пјҡжӯЈзҹ©йҳөжҖ§иҙЁгҖҒзү№еҫҒеҖје’Ңзү№еҫҒеҗ‘йҮҸгҖҒе№Ӯиҝӯд»Јз®—жі•гҖҒGauss-Seidelиҝӯд»Јз®—жі•зӯү.
- PageRank еҫ—еҲҶжҳҜд»ӢдәҺ 0 е’Ң 1 д№Ӣй—ҙзҡ„дёҖдёӘж•°,еҫ—еҲҶи¶ҠеӨ§иЎЁзӨәзҪ‘йЎөи¶ҠйҮҚиҰҒ.
4гҖҒPageRankз®—жі•жҖқжғіз®Җд»Ӣ
1пјүгҖҒPageRankеҹәдәҺеҒҮи®ҫе…ізі»
вҖңи®ёеӨҡдјҳиҙЁзҡ„зҪ‘йЎөдёӯи¶…й“ҫжҺҘзҡ„зҪ‘йЎөпјҢеҝ…е®ҡжҳҜдјҳиҙЁзҪ‘йЎөвҖқпјҢд»ҘжӯӨеҲӨе®ҡжүҖжңүзҪ‘йЎөзҡ„йҮҚиҰҒжҖ§гҖӮ
йҮҚиҰҒжҖ§з”ұиҜҘзҪ‘йЎөиў«и®ҝй—®зҡ„жҰӮзҺҮеӨ§е°ҸжқҘеҲ»з”»гҖӮ
-
еҜје…Ҙй“ҫжҺҘпјҡеҚ•зәҜж„Ҹд№үдёҠзҡ„еҸ—ж¬ўиҝҺеәҰжҢҮж Ү
-
еҜје…Ҙй“ҫжҺҘжҳҜеҗҰжқҘиҮӘеҸ—ж¬ўиҝҺзЁӢеәҰй«ҳзҡ„пјҡжңүж №жҚ®зҡ„еҸ—ж¬ўиҝҺжҢҮж Ү
-
еҜје…Ҙй“ҫжҺҘжәҗйЎөйқўзҡ„еҜјеҮәй“ҫжҺҘпјҡиў«йҖүдёӯзҡ„жҰӮзҺҮжҢҮж Ү
2пјүгҖҒPageRank жҳҜеҹәдәҺиҝҷж ·дёҖдёӘзҗҶи®әпјҡ
- иӢҘ B зҪ‘йЎөдёҠжңүиҝһжҺҘеҲ° A зҪ‘йЎөзҡ„й“ҫжҺҘ( з§° B дёә A зҡ„еҜје…Ҙй“ҫжҺҘ), иҜҙжҳҺ B и®Өдёә A жңүй“ҫжҺҘд»·еҖјпјҢжҳҜдёҖдёӘвҖңйҮҚиҰҒвҖқзҡ„зҪ‘йЎө. еҪ“ B зҪ‘йЎөзә§еҲ« ( йҮҚиҰҒжҖ§ ) жҜ”иҫғй«ҳж—¶, еҲҷA зҪ‘йЎөеҸҜд»Һ B зҪ‘йЎөиҝҷдёӘеҜје…Ҙй“ҫжҺҘеҲҶеҫ—дёҖе®ҡзҡ„зә§еҲ« ( йҮҚиҰҒжҖ§ ), 并平еқҮеҲҶй…Қз»ҷ A зҪ‘йЎөдёҠзҡ„жүҖжңүеҜјеҮәй“ҫжҺҘ.пјҲеҜјеҮәй“ҫжҺҘе°ұжҳҜзҪ‘з«ҷжҲ–иҖ…йЎөйқўдёӯжңүжҢҮеҗ‘еҲ«зҡ„зҪ‘з«ҷзҡ„й“ҫжҺҘпјү
- еңЁPageRankз®—жі•дёӯ, дёҖдёӘзҪ‘йЎөзҡ„зә§еҲ«(йҮҚиҰҒжҖ§)еӨ§иҮҙз”ұдёӢйқўдёӨдёӘеӣ зҙ еҶіе®ҡпјҡиҜҘзҪ‘йЎөзҡ„еҜје…Ҙй“ҫжҺҘзҡ„ж•°йҮҸе’ҢиҝҷдәӣеҜје…Ҙй“ҫжҺҘзҡ„зә§еҲ«(йҮҚиҰҒжҖ§).
5гҖҒPageRankи®Ўз®—
1пјүгҖҒйӮ»жҺҘзҹ©йҳө
- дә’иҒ”зҪ‘жҳҜдёҖдёӘжңүеҗ‘еӣҫ
- жҜҸдёҖдёӘзҪ‘йЎөжҳҜеӣҫзҡ„дёҖдёӘйЎ¶зӮ№
- зҪ‘йЎөй—ҙзҡ„жҜҸдёҖдёӘи¶…й“ҫжҺҘжҳҜеӣҫзҡ„дёҖдёӘжңүеҗ‘иҫ№
- з”ЁйӮ»жҺҘзҹ©йҳөGжқҘиЎЁзӨәжңүеҗ‘еӣҫ, еҚіпјҢиӢҘзҪ‘йЎөjеҲ°зҪ‘йЎөiжңүи¶…й“ҫжҺҘ,еҲҷgij=1, еҗҰеҲҷдёәgij=0.
йӮ»жҺҘзҹ©йҳөжҳҜдёҖдёӘеҚҒеҲҶеәһеӨ§жңүзӣёеҪ“зЁҖз–Ҹзҡ„ж–№йҳө(з”Ёй»‘иүІд»ЈиЎЁ1, з”ЁзҷҪиүІд»ЈиЎЁ0)
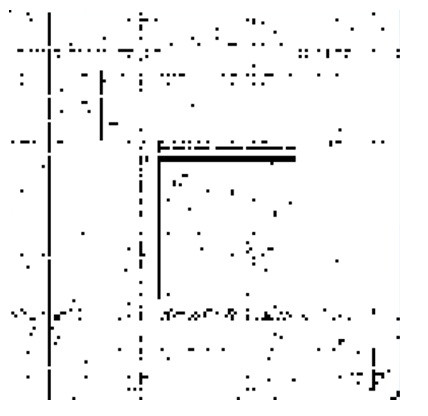
-
з”ЁйӮ»жҺҘзҹ©йҳөGжқҘиЎЁзӨәеӣҫ, еҚіпјҢиӢҘзҪ‘йЎөjеҲ°зҪ‘йЎөiжңүи¶…й“ҫжҺҘ,еҲҷgij=1, еҗҰеҲҷдёәgij=0.
-
е®ҡд№үзҹ©йҳөGзҡ„еҲ—е’ҢдёҺиЎҢе’Ң

е…¶дёӯcjпјҲеҲ—е’Ңпјү жҳҜйЎөйқўjзҡ„еҜјеҮәй“ҫжҺҘж•°зӣ®,
riпјҲиЎҢе’Ңпјү жҳҜйЎөйқўiзҡ„еҜје…Ҙй“ҫжҺҘж•°зӣ®.
2пјүгҖҒиҪ¬з§»жҰӮзҺҮзҹ©йҳө
- еҒҮи®ҫжҲ‘们еңЁдёҠзҪ‘зҡ„ж—¶еҖҷжөҸи§ҲйЎөйқўе№¶йҖүжӢ©дёӢдёҖдёӘйЎөйқў, иҝҷдёӘиҝҮзЁӢдёҺиҝҮеҺ»жөҸи§ҲиҝҮе“ӘдәӣйЎөйқўж— е…і, иҖҢд»…дҫқиө–дәҺеҪ“еүҚжүҖеңЁзҡ„йЎөйқў, йӮЈд№ҲиҝҷдёҖйҖүжӢ©иҝҮзЁӢеҸҜд»Ҙи®ӨдёәжҳҜдёҖдёӘжңүйҷҗзҠ¶жҖҒгҖҒзҰ»ж•Јж—¶й—ҙзҡ„йҡҸжңәиҝҮзЁӢ, е…¶зҠ¶жҖҒиҪ¬з§»и§„еҫӢеҸҜз”ЁMarkovй“ҫжҸҸиҝ°.
- е®ҡд№үиҪ¬з§»жҰӮзҺҮзҹ©йҳө
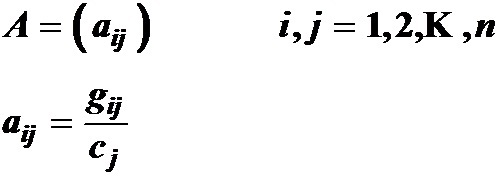
3пјүгҖҒ85%дёҺ15%
- дҪҶиҝҳиҰҒиҖғиҷ‘еҲ°з”ЁжҲ·иҷҪ然еңЁи®ёеӨҡеңәеҗҲйғҪйЎәзқҖеҪ“еүҚйЎөйқўдёӯзҡ„й“ҫжҺҘеүҚиҝӣ, дҪҶж—¶еёёеҸҲдјҡи·іи·ғеҲ°е®Ңе…Ёж— е…ізҡ„йЎөйқў.
- з»ҸиҝҮз»ҹи®Ў, GoogleйҮҮз”ЁдёӘ15%жқҘиЎЁзӨә[ж—¶еёё], еҚіз”ЁжҲ·еңЁ85%зҡ„жғ…еҶөдёӢжІҝзқҖй“ҫжҺҘеүҚиҝӣ, дҪҶжңү15%зҡ„жғ…еҶөдёӢзӘҒ然跳и·ғеҲ°ж— е…ізҡ„йЎөйқўдёӯеҺ».
- д»ҺиҖҢдҝ®жӯЈзҠ¶жҖҒиҪ¬з§»зҹ©йҳө

4пјүгҖҒзҪ‘йЎөзҡ„жңҖз»ҲPageRankеҖј.
-
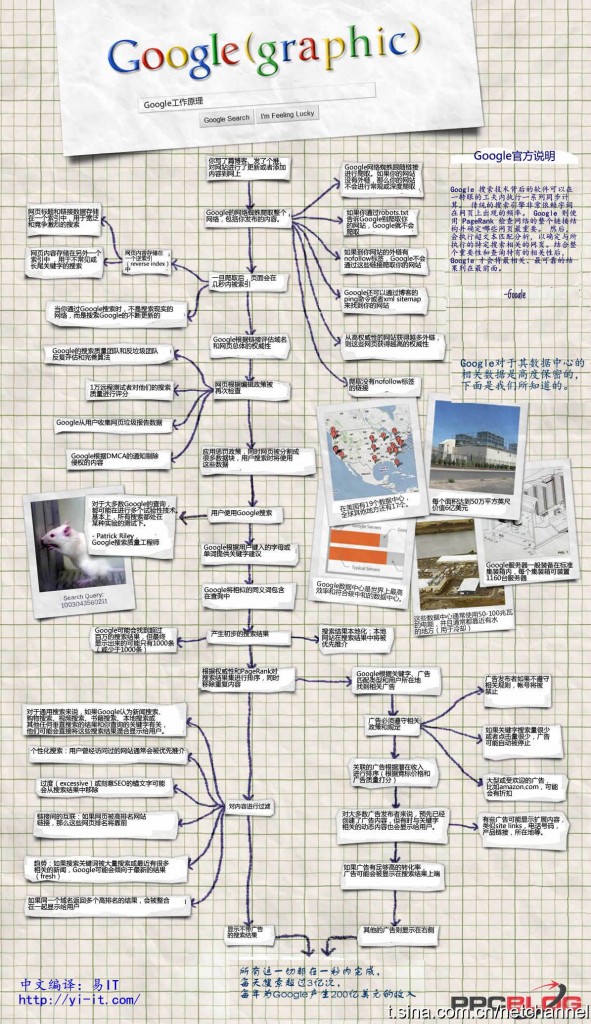
ж №жҚ®Markovй“ҫзҡ„еҹәжң¬жҖ§иҙЁ,д»ҘдёҠA' жҳҜдёҖдёӘжӯЈеҲҷMarkovй“ҫ, еӯҳеңЁе№ізЁіеҲҶеёғx= (x1,x2,x3, ...,xm),ж»Ўи¶і

- xиЎЁзӨәеңЁжһҒйҷҗзҠ¶жҖҒ(иҪ¬з§»ж¬Ўж•°и¶ӢдәҺж— йҷҗ)дёӢеҗ„зҪ‘йЎөиў«и®ҝй—®зҡ„жҰӮзҺҮеҲҶеёғ.
- xе®ҡд№үдёәзҪ‘йЎөзҡ„PageRankеҗ‘йҮҸ,xiиЎЁзӨә第iдёӘзҪ‘йЎөзҡ„PageRankеҖј.жҳҫ然жҰӮзҺҮи¶ҠеӨ§, е…¶йҮҚиҰҒжҖ§и¶Ҡй«ҳжҳҜеҗҲзҗҶзҡ„.
- еҲҶйҮҸxеә”ж»Ўи¶іж–№зЁӢ
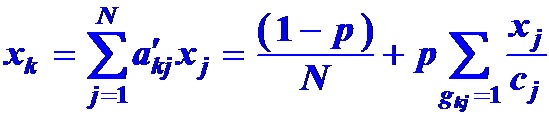
- д»ҺеҸҰдёҖи§’еәҰзңӢ, зҪ‘йЎөjе°Ҷе®ғзҡ„PageRankеҖјxjеҲҶжҲҗcjд»Ҫ, еҲҶеҲ«вҖңжҠ•зҘЁвҖқз»ҷе®ғй“ҫеҮәзҡ„зҪ‘йЎө.
- зҪ‘йЎөkзҡ„PageRankеҖјxkе°ұжҳҜжүҖжңүйЎөйқўжҠ•зҘЁз»ҷзҪ‘йЎөkзҡ„жңҖз»ҲеҖј.
5пјүгҖҒи§Јзҡ„и®Ёи®ә
з”ұMarkovжҖ§иҙЁ,A' зҡ„жңҖеӨ§зү№еҫҒеҖјжҳҜ1,еҚіжұӮзү№еҫҒеҖј1еҜ№еә”зҡ„зү№еҫҒеҗ‘йҮҸ.
й—®пјҡдёҠиҝ°ж–№зЁӢз»„зҡ„и§ЈжҳҜеҗҰе”ҜдёҖи§Јпјҹи§ЈжҳҜеҗҰжңүж„Ҹд№ү(еҚідёҚдјҡеҮәзҺ°иҙҹж•°жҲ–еӨ§дәҺ1зҡ„ж•°)пјҹ
зӯ”пјҡдёҠиҝ°ж–№зЁӢз»„зҡ„и§Је”ҜдёҖдё”еҲҶйҮҸйғҪеӨ§дәҺ0пјҒ
зҗҶз”ұпјҡPerron-Frobnius е®ҡзҗҶ.
6гҖҒPerron-Frobnius е®ҡзҗҶ
1пјүгҖҒеҰӮжһң A жҳҜжӯЈзҡ„ж–№йҳө(жүҖжңүе…ғзҙ еқҮеӨ§дәҺ0), еҲҷ
Aзҡ„и°ұеҚҠеҫ„r(A)>0пјҢе…¶дёӯl1,l2, ... ,lnдёәAзҡ„зү№еҫҒеҖјгҖӮ
l=r(A) жҳҜAзҡ„зү№еҫҒеҖј, дё”д»Јж•°йҮҚж•°дёә 1, еҚідёәеҚ•зү№еҫҒеҖјгҖӮ
еӯҳеңЁе”ҜдёҖзҡ„x>0, ж»Ўи¶іA x=x, дё”
иӢҘlжҳҜAзҡ„зү№еҫҒеҖј, дё”lВ№r(A),еҲҷ|l| <r(A) .
2пјүгҖҒl= 1 жҳҜAзҡ„зү№еҫҒеҖј(Ax=x)зҡ„з®ҖеҚ•иҜҒжҳҺ

7гҖҒзҪ‘йЎөжҺ’еҗҚдёҫдҫӢ
дҫӢпјҡз”ЁPageRank з®—жі•и®Ўз®—дёӢйқўзҡ„е°ҸеһӢзҪ‘з»ңдёӯеҗ„зҪ‘йЎөзҡ„жҺ’еҗҚ, е…¶дёӯеҸ–p=0.85.
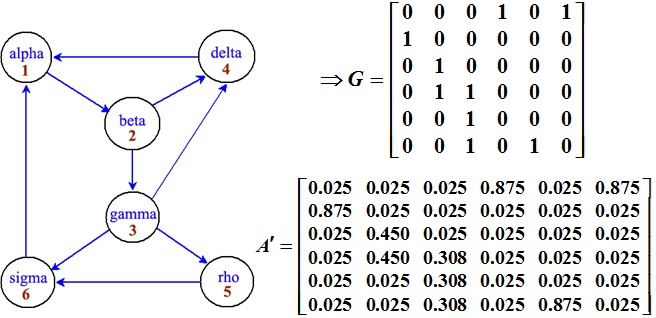
и§Јеҫ—
x= (0.2675, 0.2524, 0.1323, 0.1698, 0.0625, 0.1156)T
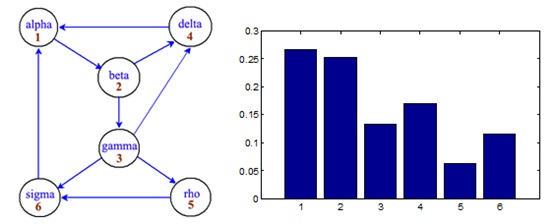
- зҪ‘йЎө1зҡ„йҮҚиҰҒжҖ§жңҖй«ҳ, иҷҪ然2зҡ„еҜје…Ҙй“ҫжҺҘж•°еҸӘжңү1, дҪҶеҚҙжҳҜзҪ‘йЎө1е”ҜдёҖзҡ„еӨ–й“ҫ, жүҖд»Ҙе…¶йҮҚиҰҒжҖ§д№ҹжҳҫи‘—жҸҗй«ҳпјҒ
- зҪ‘йЎө3иҷҪжҳҜзҪ‘йЎө2зҡ„еӨ–й“ҫ, дҪҶеҸӘиғҪеҫ—еҲ°зҪ‘йЎө2дёҖеҚҠзҡ„еҲҶж•°.
дәӢе®һдёҠ, й—®йўҳиҝҳдёҚжҳҜиҝҷд№Ҳз®ҖеҚ•пјҒ
- GoogleиҰҒйқўеҜ№дёҠзҷҫдәҝзҡ„зҪ‘йЎө, и®Ўз®—йҮҸзү№еҲ«еӨ§,
- е°Өе…¶и®Ўз®—зү№еҫҒеҖјAx=xеҜ№и®Ўз®—иғҪеҠӣиҰҒжұӮзү№еҲ«й«ҳпјҢйңҖиҰҒе…іжіЁи®Ўз®—зҡ„еӨҚжқӮеәҰпјҢиҝҷйҮҢз”ЁеҲ°и®ёеӨҡж•°еҖји®Ўз®—е·Ҙе…·гҖӮ
- жӯӨеӨ–иҝҳиҰҒи®Ёи®әзҪ‘йЎөзҡ„зҙўеј•гҖҒжҹҘиҜўзӯүж–№жі•гҖӮ
еҸӮиҖғиө„ж–ҷпјҡgoogleжҹҘиҜўжҗңзҙўеӣҫзӨәиҝҮзЁӢ
еҲҶдә«еҲ°пјҡ








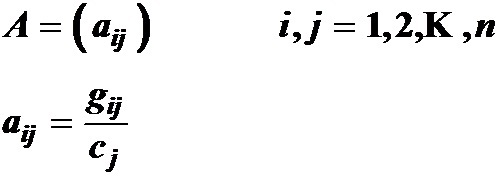


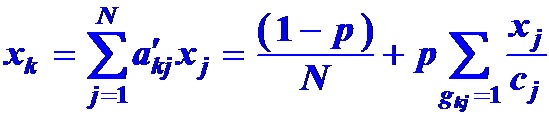






зӣёе…іжҺЁиҚҗ
гҖҠLжҗңиҒҡеҗҲжҗңзҙўеј•ж“ҺпјҡжҺўзҙўж·ұеәҰдҝЎжҒҜжЈҖзҙўзҡ„еҘҘз§ҳгҖӢ еңЁдҝЎжҒҜеҢ–ж—¶д»ЈпјҢжҗңзҙўеј•ж“Һе·Із»ҸжҲҗдёәжҲ‘们иҺ·еҸ–дҝЎжҒҜгҖҒи§ЈеҶій—®йўҳзҡ„йҮҚиҰҒе·Ҙе…·гҖӮLжҗңиҒҡеҗҲжҗңзҙўеј•ж“ҺдҪңдёәдёҖдёӘзӢ¬зү№зҡ„еӯҳеңЁпјҢе®ғдёҚд»…ж•ҙеҗҲдәҶеӨҡз§ҚжҗңзҙўжҠҖжңҜпјҢиҝҳе…·еӨҮдәҶејәеӨ§зҡ„дҝЎжҒҜиҒҡеҗҲиғҪеҠӣпјҢ...
еңЁITиЎҢдёҡдёӯпјҢ"жҗңзҙўзӢӮйЈҷ"еҸҜиғҪжҳҜжҢҮдёҖз§Қжҗңзҙўеј•ж“ҺдјҳеҢ–пјҲSearch Engine Optimization, SEOпјүжҲ–жҗңзҙўеј•ж“ҺиҗҘй”ҖпјҲSearch Engine Marketing, SEMпјүзҡ„зӯ–з•ҘпјҢж—ЁеңЁжҸҗеҚҮзҪ‘з«ҷеңЁжҗңзҙўеј•ж“Һз»“жһңдёӯзҡ„жҺ’еҗҚпјҢд»ҺиҖҢеўһеҠ е…¶еҸҜи§ҒжҖ§е’ҢжөҒйҮҸгҖӮ...
### иҝҷе°ұжҳҜжҗңзҙўеј•ж“Һпјҡж ёеҝғжҠҖжңҜиҜҰи§Ј #### жҗңзҙўеј•ж“ҺжҰӮиҝ° жҗңзҙўеј•ж“ҺжҳҜдә’иҒ”зҪ‘дёҠжҸҗдҫӣдҝЎжҒҜжЈҖзҙўжңҚеҠЎзҡ„дёҖз§Қе·Ҙе…·жҲ–зі»з»ҹпјҢз”ЁжҲ·еҸҜд»ҘйҖҡиҝҮиҫ“е…Ҙе…ій”®иҜҚзҡ„ж–№ејҸжҹҘиҜўжүҖйңҖзҡ„дҝЎжҒҜ...еёҢжңӣжң¬зҜҮж–Үз« иғҪеё®еҠ©еӨ§е®¶жӣҙж·ұе…Ҙең°зҗҶи§Јжҗңзҙўеј•ж“ҺиғҢеҗҺзҡ„еҘҘз§ҳпјҒ
е…¶дёӯпјҢGoogleжҗңзҙўеј•ж“Һд»Ҙе…¶й«ҳж•ҲгҖҒзІҫеҮҶзҡ„жҗңзҙўиғҪеҠӣдә«иӘүе…ЁзҗғгҖӮеҜ№дәҺејҖеҸ‘иҖ…иҖҢиЁҖпјҢз ”з©¶е…¶жәҗз ҒдёҚд»…еҸҜд»ҘжҸҗеҚҮжҠҖжңҜж°ҙе№іпјҢиҝҳиғҪеҜ№жҗңзҙўеј•ж“Һзҡ„е·ҘдҪңеҺҹзҗҶжңүжӣҙж·ұе…Ҙзҡ„зҗҶи§ЈгҖӮжң¬зҜҮж–Үз« е°ҶиҒҡз„ҰдәҺдёҖж¬ҫеҹәдәҺVBпјҲVisual Basicпјүзј–еҶҷзҡ„жЎҢйқўGoogle...
йҡҸзқҖж—¶й—ҙзҡ„еҸ‘еұ•пјҢGoogleзҡ„з®—жі•дёҚж–ӯиҝӣеҢ–пјҢеҠ е…ҘдәҶжӣҙеӨҡзҡ„еӣ зҙ пјҢеҰӮеҶ…е®№иҙЁйҮҸгҖҒе…ій”®иҜҚгҖҒз”ЁжҲ·иЎҢдёәжЁЎејҸзӯүпјҢеҪўжҲҗдәҶдёҖдёӘеҗҚдёәвҖңGoogleжҗңзҙўжҺ’еҗҚвҖқзҡ„з»јеҗҲзі»з»ҹгҖӮ еҺӢзј©еҢ…дёӯзҡ„"googler-master"еҸҜиғҪеҢ…еҗ«дәҶGoogleз®—жі•зҡ„е®һзҺ°д»Јз ҒжҲ–зӣёе…і...
1. жҗңзҙўеј•ж“Һд»Ӣз»Қпјҡи®Іи§Јжҗңзҙўеј•ж“Һзҡ„дҪңз”ЁпјҢеҰӮGoogleгҖҒBingгҖҒзҷҫеәҰзӯүдё»жөҒеј•ж“Һзҡ„зү№зӮ№е’Ңе·®ејӮпјҢи®©еӯҰз”ҹеҲқжӯҘдәҶи§Је…¶е·ҘдҪңеҺҹзҗҶгҖӮ 2. еҹәжң¬жҗңзҙўжҠҖе·§пјҡйҖҡиҝҮе®һдҫӢжј”зӨәпјҢж•ҷдјҡеӯҰз”ҹеҰӮдҪ•жӯЈзЎ®иҫ“е…Ҙе…ій”®иҜҚпјҢйҒҝе…Қж— ж•ҲжҗңзҙўгҖӮејәи°ғе…ій”®иҜҚзҡ„жҸҗзӮјдёҺ...
**SEOпјҲжҗңзҙўеј•ж“ҺдјҳеҢ–пјүжҳҜдә’иҒ”зҪ‘иҗҘй”ҖйўҶеҹҹдёӯзҡ„е…ій”®жҰӮеҝөпјҢе®ғж¶үеҸҠеҰӮдҪ•жҸҗй«ҳзҪ‘з«ҷеңЁжҗңзҙўеј•ж“Һз»“жһңйЎөйқўдёҠзҡ„жҺ’еҗҚпјҢд»ҺиҖҢеҗёеј•жӣҙеӨҡзҡ„иҮӘ然жөҒйҮҸгҖӮжң¬ж•ҷзЁӢеҹәдәҺдёҖдёӘPPTж–Ү件пјҢеҗҚдёә"seo.ppt"пјҢе°Ҷж·ұе…ҘжҺўи®ЁSEOзҡ„еҹәжң¬еҺҹзҗҶгҖҒзӯ–з•Ҙе’ҢжҠҖе·§гҖӮ** ...
дј з»ҹзҡ„жҗңзҙўеј•ж“ҺеҰӮзҷҫеәҰгҖҒи°·жӯҢзӯүпјҢе·Із»ҸдёәжҲ‘们жҸҗдҫӣдәҶдё°еҜҢзҡ„зҪ‘з»ңиө„жәҗжЈҖзҙўжңҚеҠЎгҖӮ然иҖҢпјҢйҡҸзқҖеҢәеқ—й“ҫжҠҖжңҜе’ҢеҲҶеёғејҸи®Ўз®—зҡ„еҸ‘еұ•пјҢдёҖз§Қж–°еһӢзҡ„жҗңзҙўж–№ејҸвҖ”вҖ”P2PSearchпјҲеҜ№зӯүзҪ‘з»ңжҗңзҙўпјүеә”иҝҗиҖҢз”ҹпјҢе®ғжү“з ҙдәҶдј з»ҹзҡ„дёӯеҝғеҢ–жҗңзҙўжЁЎејҸпјҢдёә...
гҖҗSEOи§Ҷйў‘ж•ҷзЁӢгҖ‘\n\nжң¬ж•ҷзЁӢз”ұжӣ№й№Ҹдё»и®ІпјҢж·ұе…Ҙжө…еҮәең°и§ЈжһҗSEOпјҲSearch Engine OptimizationпјҢжҗңзҙўеј•ж“ҺдјҳеҢ–пјүзҡ„еҘҘз§ҳгҖӮSEOжҳҜдә’иҒ”зҪ‘иҗҘй”ҖйўҶеҹҹзҡ„йҮҚиҰҒзӯ–з•ҘпјҢе®ғж—ЁеңЁйҖҡиҝҮдјҳеҢ–зҪ‘з«ҷеҶ…е®№гҖҒз»“жһ„е’ҢеӨ–йғЁй“ҫжҺҘпјҢдҪҝзҪ‘з«ҷеңЁжҗңзҙўеј•ж“Һзҡ„иҮӘ然...
жӯӨеӨ–пјҢеӨ§йғЁеҲҶжҗңзҙўеј•ж“ҺйғҪжңүиҮӘе·ұзҡ„APIпјҢеҰӮGoogleзҡ„Custom Search JSON APIпјҢйҖҡиҝҮи°ғз”ЁиҝҷдәӣAPIеҸҜд»ҘиҺ·еҸ–з»“жһ„еҢ–зҡ„жҗңзҙўз»“жһңпјҢдҪҶйҖҡеёёйңҖиҰҒAPIеҜҶй’ҘпјҢ并且еҸҜиғҪжңүдҪҝз”ЁйҷҗеҲ¶гҖӮ еӯҰд№ VBзҡ„зҪ‘з»ңжҗңзҙўеҠҹиғҪдёҚд»…еҸҜд»Ҙеё®еҠ©ејҖеҸ‘иҖ…дәҶи§ЈзҪ‘з»ң...
ејҖеҸ‘иҖ…йңҖиҰҒиҺ·еҸ–Google APIеҜҶй’Ҙе’Ңжҗңзҙўеј•ж“ҺIDпјҢ然еҗҺеңЁTracзҡ„й…ҚзҪ®дёӯи®ҫзҪ®пјҢиҝҷж ·Tracз”ЁжҲ·е°ұиғҪеңЁйЎ№зӣ®з•ҢйқўеҶ…иҝӣиЎҢGoogleжҗңзҙўдәҶгҖӮ жҖ»з»“жқҘиҜҙпјҢTracGoogleSearch-0.1.0жҳҜдёҖдёӘеўһејәTracеҠҹиғҪзҡ„Pythonеә“пјҢе®ғйҖҡиҝҮйӣҶжҲҗGoogleжҗңзҙўпјҢ...
1. **жҗңзҙўеј•ж“Һзҙўеј•жӣҙж–°**пјҡжҗңзҙўеј•ж“ҺеҰӮзҷҫеәҰгҖҒGoogleзӯүпјҢеҲ©з”ЁWebRobotе®ҡжңҹжҠ“еҸ–зҪ‘йЎөпјҢжӣҙж–°зҙўеј•еә“гҖӮ 2. **еёӮеңәеҲҶжһҗ**пјҡдјҒдёҡеҸҜд»ҘеҲ©з”ЁWebRobotжҠ“еҸ–з«һдәүеҜ№жүӢзҡ„дә§е“ҒдҝЎжҒҜгҖҒд»·ж јеҠЁжҖҒпјҢиҝӣиЎҢеёӮеңәеҲҶжһҗгҖӮ 3. **ж–°й—»зӣ‘жҺ§**пјҡиҮӘеҠЁ...
еҸҜиғҪдјҡж¶үеҸҠеҲ°еҰӮдҪ•иҝһжҺҘзҪ‘з»ңгҖҒи®ҫзҪ®и·Ҝз”ұеҷЁгҖҒзҪ‘з»ңе®үе…ЁйҳІиҢғгҖҒз”өеӯҗйӮ®д»¶зҡ„дҪҝз”Ёд»ҘеҸҠжҗңзҙўеј•ж“ҺдјҳеҢ–зӯүеҶ…е®№гҖӮиҝҷйғЁеҲҶзҹҘиҜҶеҜ№дәҺж—Ҙеёёз”ҹжҙ»е’Ңе·ҘдҪңдёӯзҡ„зҪ‘з»ңеә”з”ЁиҮіе…ійҮҚиҰҒгҖӮ жӯӨеӨ–пјҢеҠһе…¬иҪҜ件зҡ„еә”з”ЁжҠҖе·§д№ҹеҸҜиғҪжҳҜиө„ж–ҷзҡ„йҮҚзӮ№пјҢдҫӢеҰӮMicrosoft ...
йҒҮеҲ°еӣ°йҡҫж—¶пјҢдёҚеә”з«ӢеҲ»жұӮеҠ©д»–дәәпјҢиҖҢжҳҜиҰҒеӯҰдјҡеҲ©з”Ёжҗңзҙўеј•ж“ҺпјҲеҰӮзҷҫеәҰгҖҒGoogleпјүжҹҘжүҫзӯ”жЎҲпјҢдәҶи§Јй—®йўҳиғҢеҗҺзҡ„еҺҹеӣ гҖӮиҝҷдёҚд»…иғҪжҸҗеҚҮиҮӘжҲ‘и§ЈеҶій—®йўҳзҡ„иғҪеҠӣпјҢд№ҹжңүеҠ©дәҺд»ҺиҸңйёҹжҲҗй•ҝдёәй«ҳжүӢгҖӮ жҖ»д№ӢпјҢBIOSи®ҫзҪ®е№¶йқһй«ҳж·ұиҺ«жөӢпјҢеҸӘйңҖдәҶи§Јеҹәжң¬...
- **жҗңзҙўеј•ж“Һиҝҗз”Ё**пјҡеӯҰз”ҹйңҖжҺҢжҸЎеҰӮдҪ•й«ҳж•Ҳең°дҪҝз”Ёжҗңзҙўеј•ж“ҺжқҘжҹҘжүҫзӣёе…ідҝЎжҒҜпјҢеҰӮGoogleжҲ–зҷҫеәҰзӯүгҖӮ - **FrontPageзҡ„дҪҝз”Ё**пјҡеӯҰз”ҹеә”еӯҰдјҡдҪҝз”ЁMicrosoft FrontPageжқҘеҲӣе»әдёӘдәәжҲ–е°Ҹз»„зҡ„дё“йўҳзҪ‘з«ҷпјҢеұ•зӨәз ”з©¶жҲҗжһңгҖӮ - **Wordж–ҮжЎЈ...
"03-pagerank.pdf"йҮҚзӮ№жҳҜGoogleзҡ„PageRankз®—жі•пјҢиҝҷжҳҜжҗңзҙўеј•ж“ҺжҺ’еҗҚзҡ„е…ій”®жҠҖжңҜгҖӮиҜҘз®—жі•еҲ©з”ЁзҪ‘з»ңзҡ„й“ҫжҺҘз»“жһ„жқҘиҜ„дј°зҪ‘йЎөзҡ„йҮҚиҰҒжҖ§пјҢе®ғдёҚд»…еңЁдә’иҒ”зҪ‘жҗңзҙўдёӯеҸ‘жҢҘйҮҚиҰҒдҪңз”ЁпјҢд№ҹжҳҜзҪ‘з»ңеҲҶжһҗдёӯзҡ„дёҖдёӘз»Ҹе…ёжЎҲдҫӢгҖӮеӯҰз”ҹе°ҶеӯҰд№ PageRank...
ж–ҮжЎЈеҸҜиғҪдјҡи®Ёи®әеҰӮдҪ•еҲ©з”Ёжҗңзҙўеј•ж“ҺгҖҒStack Overflowзӯүиө„жәҗпјҢд»ҘеҸҠеҰӮдҪ•иҝҗз”Ёи°ғиҜ•жҠҖе·§жқҘе®ҡдҪҚе’Ңи§ЈеҶій—®йўҳгҖӮ 6. **иЎҢдёҡи¶ӢеҠҝдёҺжңӘжқҘ**пјҡйҡҸзқҖ科жҠҖзҡ„еҸ‘еұ•пјҢзЁӢеәҸе‘ҳйңҖиҰҒе…іжіЁж–°е…ҙжҠҖжңҜпјҢеҰӮдәәе·ҘжҷәиғҪгҖҒеҢәеқ—й“ҫгҖҒзү©иҒ”зҪ‘зӯүгҖӮж–ҮжЎЈеҸҜиғҪдјҡ...
2. **SEOдјҳеҢ–**пјҡз”ұдәҺAjaxеҠ иҪҪзҡ„еҶ…е®№еҜ№жҗңзҙўеј•ж“ҺдёҚеҸӢеҘҪпјҢеҸҜд»ҘйҖҡиҝҮжңҚеҠЎеҷЁз«ҜжёІжҹ“жҲ–йў„жёІжҹ“жҠҖжңҜж”№е–„гҖӮ 3. **еӣһйҖҖжңәеҲ¶**пјҡиҖғиҷ‘жІЎжңүJavaScriptзҡ„зҺҜеўғпјҢеҸҜд»ҘдҪҝз”Ёйҡҗи—Ҹзҡ„иЎЁеҚ•жҲ–й“ҫжҺҘдҪңдёәеӨҮйҖүж–№жЎҲгҖӮ жҖ»д№ӢпјҢAjaxжҠҖжңҜжҳҜзҺ°д»ЈWeb...
дҫӢеҰӮпјҢPageRankз®—жі•жҳҜGoogleжҗңзҙўеј•ж“ҺжҺ’еҗҚзҡ„ж ёеҝғпјҢе®ғйҖҡиҝҮиҖғиҷ‘зҪ‘йЎөй—ҙзҡ„й“ҫжҺҘе…ізі»жқҘиҜ„дј°зҪ‘йЎөзҡ„йҮҚиҰҒзЁӢеәҰгҖӮжӯӨеӨ–пјҢиҝҳжңүжңҖзҹӯи·Ҝеҫ„з®—жі•пјҢеҰӮDijkstraз®—жі•пјҢз”ЁдәҺжүҫеҮәзҪ‘з»ңдёӯдёӨдёӘиҠӮзӮ№д№Ӣй—ҙзҡ„жңҖзҹӯи·Ҝеҫ„пјҢиҝҷеҜ№дәҺзҪ‘з»ңи·Ҝз”ұе’Ңиө„жәҗеҲҶй…ҚиҮіе…і...