- 浏览: 4424015 次
- 性别:

- 来自: 湛江
-

博客专栏
-

-
SQLite源码剖析
浏览量:80254
-

-
WIN32汇编语言学习应用...
浏览量:70671
-

-
神奇的perl
浏览量:103850
-

-
lucene等搜索引擎解析...
浏览量:287078
-

-
深入lucene3.5源码...
浏览量:15096
-

-
VB.NET并行与分布式编...
浏览量:68117
-

-
silverlight 5...
浏览量:32429
-

-
算法下午茶系列
浏览量:46191
最新评论
-
yoyo837:
counters15 写道目前只支持IE吗?插件的东西是跨浏览 ...
Silverlight 5 轻松开启绚丽的网页3D世界 -
shuiyunbing:
直接在前台导出方式:excel中的单元格样式怎么处理,比如某行 ...
Flex导出Excel -
di1984HIT:
写的很好~
lucene入门-索引网页 -
rjguanwen:
在win7 64位操作系统下,pygtk的Entry无法输入怎 ...
pygtk-entry -
ldl_xz:
http://www.9958.pw/post/php_exc ...
PHPExcel常用方法汇总(转载)
![deepfuture的博客: 深未来(深度创造未来)[deepfuture@yeah.net] deepfuture的博客](https://www.iteye.com/upload/logo/user/690059/d08c7f3a-9298-3a06-9235-0d0226833f0a.jpg?1717538039)

 ,假定其概率密度函数(连续分布)或概率聚集函数(离散分布)为
,假定其概率密度函数(连续分布)或概率聚集函数(离散分布)为 ,以及一个分布参数
,以及一个分布参数 ,我们可以从这个分布中抽出一个具有
,我们可以从这个分布中抽出一个具有 个值的采样
个值的采样 ,通过利用
,通过利用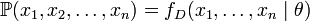
 ,然后用这些采样数据来估计
,然后用这些采样数据来估计
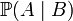 。
。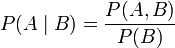
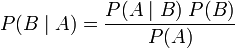
 ,我们估计参数B的可能性。形式上,似然函数也是一种条件概率函数,但我们关注的变量改变了:
,我们估计参数B的可能性。形式上,似然函数也是一种条件概率函数,但我们关注的变量改变了:
 。一个似然函数乘以一个正的常数之后仍然是似然函数。对所有
。一个似然函数乘以一个正的常数之后仍然是似然函数。对所有 ,都可以有似然函数:
,都可以有似然函数:
 值即被称为
值即被称为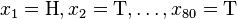 并把正面的次数记下来,正面记为H,反面记为T)。并把抛出一个正面的概率记为
并把正面的次数记下来,正面记为H,反面记为T)。并把抛出一个正面的概率记为 ,抛出一个反面的概率记为
,抛出一个反面的概率记为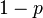 (因此,这里的
(因此,这里的 ,
,  ,
,  .这些硬币没有标记,所以我们无法知道哪个是哪个。使用最大似然估计,通过这些试验数据(即采样数据),我们可以计算出哪个硬币的可能性最大。这个似然函数取以下三个值中的一个:
.这些硬币没有标记,所以我们无法知道哪个是哪个。使用最大似然估计,通过这些试验数据(即采样数据),我们可以计算出哪个硬币的可能性最大。这个似然函数取以下三个值中的一个: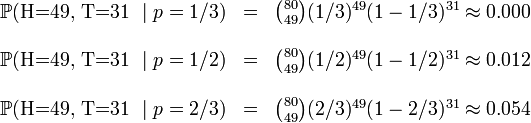
 时,似然函数取得最大值。这就是
时,似然函数取得最大值。这就是 中的任何一个
中的任何一个
![\begin{matrix}
0 & = & \frac{d}{dp} \left( \binom{80}{49} p^{49}(1-p)^{31} \right) \\
& & \\
& \propto & 49p^{48}(1-p)^{31} - 31p^{49}(1-p)^{30} \\
& & \\
& = & p^{48}(1-p)^{30}\left[ 49(1-p) - 31p \right] \\
\end{matrix}](http://upload.wikimedia.org/wikipedia/zh/math/f/4/3/f43c984e21445732edf403445fe32ea9.png)

 ,
,  ,以及
,以及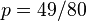 .使可能性最大的解显然是
.使可能性最大的解显然是 .
. 代替49用以表达伯努利试验中的被观察数据(即样本)的“成功”次数,用另一个字母
代替49用以表达伯努利试验中的被观察数据(即样本)的“成功”次数,用另一个字母
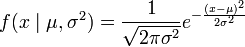

 ,
,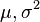 .有人可能会担心两个参数与上边的讨论的例子不同,上边的例子都只是在一个参数上对可能性进行最大化。实际上,在两个参数上的求最大值的方法也差不多:只需要分别把可能性
.有人可能会担心两个参数与上边的讨论的例子不同,上边的例子都只是在一个参数上对可能性进行最大化。实际上,在两个参数上的求最大值的方法也差不多:只需要分别把可能性 在两个参数上最大化即可。当然这比一个参数麻烦一些,但是一点也不复杂。使用上边例子同样的符号,我们有
在两个参数上最大化即可。当然这比一个参数麻烦一些,但是一点也不复杂。使用上边例子同样的符号,我们有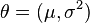 .
.
 .这的确是这个函数的最大值,因为它是
.这的确是这个函数的最大值,因为它是 里头惟一的一阶导数等于零的点并且二阶导数严格小于零。
里头惟一的一阶导数等于零的点并且二阶导数严格小于零。 求导,并使其为零。
求导,并使其为零。
 .
.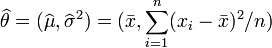



相关推荐
极大似然估计(Maximum Likelihood Estimation, MLE)是一种在统计学中广泛使用的参数估计方法,它通过寻找使得数据出现概率最大的参数值来进行估计。在这个"极大似然估计matlab代码"中,我们看到作者使用MATLAB这一...
解这两个方程,我们可以得到μ和σ的极大似然估计: μMLE = Σ(xi) / n (样本均值) σ²MLE = ∑(xi - μMLE)^2 / (n - 1) (样本方差,注意除以n-1得到无偏估计) 这里,μMLE是所有样本值的平均,而σ²MLE是...
在介绍sta中极大似然估计(MLE)方法之前,有必要了解一些统计学中关于极大似然估计的基础知识。 极大似然估计是一种用于参数估计的方法。其核心思想是在一组参数下,假定观测到的数据的概率分布最有可能出现。在...
当我们有一组观测数据,并且有一个包含未知参数的模型时,极大似然估计就是找出使数据出现概率最大的参数值。这个最大概率被称为“似然函数”,而找到的参数估计就是“极大似然估计”。这种方法在许多领域都有应用,...
极大似然估计方法(Maximum Likelihood Estimate,MLE)也称为最大概似估计或最大似然估计,是求估计的另一种方法,最大概似1821年首先由德国数学家C. F. Gauss提出,但是这个方法通常被归功于英国的统计学家R. A. ...
极大似然估计(Maximum Likelihood Estimation, MLE)是确定模型参数的一种常用方法,它通过最大化观测数据出现的概率来估计未知参数。在这个主题中,我们将深入探讨如何在MATLAB环境中使用极大似然估计来估计正态...
### 高斯分布参数的极大似然估计与EM算法 #### 一、高斯分布参数的极大似然估计 在统计学中,极大似然估计(Maximum Likelihood Estimation, MLE)是一种常用的方法,用于从给定的数据集中估计模型参数。当我们...
最大似然估计与最大后验估计 最大似然估计(Maximum Likelihood Estimation,MLE)是一种统计学方法,用于估计模型参数。它的基本思想是:给定观察数据,找出使该数据出现的概率最大的模型参数。MLE 方法的优点是...
运用区间估计的思想,提出了一种解决上述问题的评价和判断的方法,并应用此方法对完全样本情况下,形状参数的极大似然估计量的精度进行了讨论。工程上,可以依据文中提供的结论定量分析威布尔分布形状参数极大似然...
假设我们有一组观测数据,极大似然估计的目标是找到一组参数,使得这组数据出现的概率最大。 在MATLAB中实现Copula的极大似然估计,首先需要对数据进行预处理,包括确定边际分布类型(如正态、指数、对数正态等)并...
《逻辑回归(logistic regression)的本质——极大似然估计》 逻辑回归是一种广泛应用的分类方法,它虽然名字中含有“回归”,但实际上是解决分类问题的一种有效工具。逻辑回归的核心思想是通过引入Sigmoid函数,将...
2. **求解似然函数的最大值**:接下来,我们求解似然函数的最大值,这可以通过求导数并令其等于零来实现,得到的解就是极大似然估计。对于非线性问题,可能需要使用迭代方法,如梯度上升或牛顿法。 3. **解算系统...
Copula极大似然估计是统计学中用于估计联合分布的一种方法,特别是在处理多元随机变量的依赖关系时非常有用。在金融和经济领域,数据往往具有复杂的依赖结构,Copula模型可以有效地刻画这种依赖,而极大似然估计则是...
极大似然估计程序代码
极大似然估计的目标是找到一个参数估计值\( \hat{\theta} \),使得该参数下观察到的样本出现的概率最大。即求解以下问题: \[ \hat{\theta} = \arg\max_{\theta} L(\theta | X) \] 其中,\( L(\theta | X) \)称为...
最大似然估计matlab代码
本文将深入探讨“系统辨识极大似然估计法”这一核心方法,以及如何在实际应用中使用它。 系统辨识是研究和构建动态系统数学模型的过程。这些模型可以用于预测系统的未来行为、控制器设计、故障诊断等。在系统辨识中...
MLE(极大似然估计)是一种在统计学中广泛使用的参数估计方法,用于估计模型中的未知参数。这种方法基于最大似然原则,即寻找使样本数据出现概率最大的参数值。在Stata软件中,我们可以利用其内置的功能进行MLE估计...
极大似然估计(MLE)就是选择参数值θ,使得对数似然函数达到最大值。这一参数值通常记作^θn。根据样本数据来估计模型参数的基本要求是估计量应具备一定的优良性质,极大似然估计就具有以下性质: 1. 相合性...
统计信号处理作业牛顿法求最大似然估计matlab,题目为xn = sign(b*sn +wn), sn、xn已知,wn为高斯白噪声,求b的最大似然估计,不喜勿喷