é‚£ن¹ˆçگ†وƒ³ن¸çڑ„و ‘ه‹ç»“و„ه؛”ه…·ه¤‡ه“ھن؛›ç‰¹ç‚¹ه‘¢ï¼ںو•°وچ®هکه‚¨ه†—ن½™ه°ڈم€پ直观و€§ه¼؛ï¼›و–¹ن¾؟è؟”ه›و•´ن¸ھو ‘ه‹ç»“و„و•°وچ®ï¼›هڈ¯ن»¥ه¾ˆè½»و¾çڑ„è؟”ه›وںگن¸€هگو ‘(و–¹ن¾؟هˆ†ه±‚هٹ 载);ه؟«و•´èژ·ن»¥وںگèٹ‚点çڑ„祖谱路ه¾„ï¼›وڈ’ه…¥م€پهˆ 除م€پ移هٹ¨èٹ‚点و•ˆçژ‡é«کç‰ç‰م€‚ه¸¦ç€è؟™ن؛›éœ€و±‚وˆ‘وں¥و‰¾ن؛†ه¾ˆه¤ڑ资و–™ï¼Œهڈ‘çژ°ن؛†ن¸€ç§چçگ†وƒ³çڑ„و ‘ه‹ç»“و„و•°وچ®هکه‚¨هڈٹو“چن½œç®—و³•ï¼Œو”¹è؟›çڑ„ه‰چه؛ڈéپچهژ†و ‘و¨،ه‹ï¼ˆThe Nested Set Model)م€‚
هژںçگ†ï¼ڑ
آ آ آ وˆ‘ن»¬ه…ˆوٹٹو ‘وŒ‰ç…§و°´ه¹³و–¹ه¼ڈو‘†ه¼€م€‚ن»ژو ¹èٹ‚点ه¼€ه§‹ï¼ˆâ€œFoodâ€ï¼‰ï¼Œç„¶هگژن»–çڑ„ه·¦è¾¹ه†™ن¸ٹ1م€‚然هگژوŒ‰ç…§و ‘çڑ„é،؛ه؛ڈ(ن»ژن¸ٹهˆ°ن¸‹ï¼‰ç»™â€œFruitâ€çڑ„ه·¦è¾¹ه†™ن¸ٹ2م€‚è؟™و ·ï¼Œن½ و²؟ç€و ‘çڑ„边界走ه•ٹ走(è؟™ه°±وک¯â€œéپچهژ†â€ï¼‰ï¼Œç„¶هگژهگŒو—¶هœ¨و¯ڈن¸ھèٹ‚点çڑ„ه·¦è¾¹ه’Œهڈ³è¾¹ه†™ن¸ٹو•°ه—م€‚وœ€هگژ,وˆ‘ن»¬ه›هˆ°ن؛†و ¹èٹ‚点“Foodâ€هœ¨هڈ³è¾¹ه†™ن¸ٹ18م€‚ن¸‹é¢وک¯و ‡ن¸ٹن؛†و•°ه—çڑ„و ‘,هگŒو—¶وٹٹéپچهژ†çڑ„é،؛ه؛ڈ用ç®ه¤´و ‡ه‡؛و¥ن؛†م€‚
آ
آ آ آ 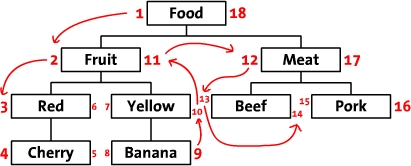
وˆ‘ن»¬ç§°è؟™ن؛›و•°ه—ن¸؛ه·¦ه€¼ه’Œهڈ³ه€¼ï¼ˆه¦‚,“Foodâ€çڑ„ه·¦ه€¼وک¯1,هڈ³ه€¼وک¯18)م€‚و£ه¦‚ن½ و‰€è§پ,è؟™ن؛›و•°ه—وŒ‰و—¶ن؛†و¯ڈن¸ھèٹ‚点ن¹‹é—´çڑ„ه…³ç³»م€‚ه› ن¸؛“Redâ€وœ‰3ه’Œ6ن¸¤ن¸ھه€¼ï¼Œو‰€ن»¥ï¼Œه®ƒوک¯وœ‰و‹¥وœ‰1-18ه€¼çڑ„“Foodâ€èٹ‚点çڑ„هگژç»م€‚هگŒو ·çڑ„,وˆ‘ن»¬هڈ¯ن»¥وژ¨و–و‰€وœ‰ه·¦ه€¼ه¤§ن؛ژ2ه¹¶ن¸”هڈ³ه€¼ه°ڈن؛ژ11çڑ„èٹ‚点,都وک¯وœ‰2-11çڑ„“Fruit†èٹ‚点çڑ„هگژç»م€‚è؟™و ·ï¼Œو ‘çڑ„结و„ه°±é€ڑè؟‡ه·¦ه€¼ه’Œهڈ³ه€¼ه‚¨هکن¸‹و¥ن؛†م€‚è؟™ç§چو•°éپچو•´و£µو ‘ç®—èٹ‚点çڑ„و–¹و³•هڈ«هپڑ“و”¹è؟›ه‰چه؛ڈéپچهژ†و ‘â€ç®—و³•م€‚
è،¨ç»“و„设è®،ï¼ڑ

é‚£ن¹ˆوˆ‘ن»¬و€ژو ·و‰چ能é€ڑè؟‡ن¸€ن¸ھSQLè¯هڈ¥وٹٹو‰€وœ‰çڑ„هˆ†ç±»éƒ½وں¥è¯¢ه‡؛و¥ه‘¢ï¼Œè€Œن¸”è¦پو±‚ه¦‚وœوک¯هگç±»çڑ„è¯ه‰چé¢è¦پو‰“ه‡ ن¸ھç©؛و ¼ن»¥è،¨çژ°وک¯هگهˆ†ç±»م€‚è¦پوƒ³وں¥è¯¢ه‡؛و‰€وœ‰هˆ†ç±»ه¾ˆه¥½هٹï¼ڑSELECT * FROM category WHERE lft>1 AND lft<18 ORDER BY lftè؟™و ·çڑ„è¯و‰€وœ‰çڑ„هˆ†ç±»éƒ½ه‡؛و¥ن؛†ï¼Œن½†وک¯è°پوک¯è°پçڑ„هگç±»هچ´هˆ†ن¸چو¸…,那ن¹ˆو€ژن¹ˆهٹه‘¢?وˆ‘ن»¬ن»”细看ه›¾ن¸چéڑ¾هڈ‘çژ°ه¦‚وœç›¸é‚»çڑ„ن¸¤و،è®°ه½•çڑ„هڈ³ه€¼ç¬¬ن¸€و،çڑ„هڈ³ه€¼و¯”第ن؛Œو،çڑ„ه¤§é‚£ن¹ˆه°±وک¯ن»–çڑ„父类,و¯”ه¦‚foodçڑ„هڈ³ه€¼وک¯18而fruitçڑ„هڈ³ه€¼وک¯11 é‚£ن¹ˆfoodوک¯fruitçڑ„父类,ن½†وک¯هڈˆè¦پ考虑هˆ°ه¤ڑç؛§ç›®ه½•م€‚ن؛ژوک¯وœ‰ن؛†è؟™و ·çڑ„设è®،,وˆ‘ن»¬ç”¨ن¸€ن¸ھو•°ç»„و¥هکه‚¨ن¸ٹن¸€و،è®°ه½•çڑ„هڈ³ه€¼ï¼Œه†چوٹٹه®ƒه’Œوœ¬و،è®°ه½•çڑ„هڈ³ه€¼و¯”较,ه¦‚وœه‰چ者و¯”هگژ者ه°ڈ,说وکژن¸چوک¯çˆ¶هگه…³ç³»ï¼Œه°±ç”¨array_popه¼¹ه‡؛و•°ç»„,هگ¦هˆ™ه°±ن؟留,ن¹‹هگژو ¹وچ®و•°ç»„çڑ„ه¤§ه°ڈو¥و‰“هچ°ç©؛و ¼م€‚è؟™و ·ه°±è§£ه†³ن؛†è؟™ن¸ھé—®é¢کم€‚ن»£ç په¦‚ن¸‹
è،¨ç»“و„ï¼ڑ
--
-- è،¨çڑ„结و„ `category`
--
CREATE TABLE IF NOT EXISTS `category` (
آ `id` int(11) NOT NULL AUTO_INCREMENT,
آ `type` int(11) NOT NULL COMMENT '1ن¸؛و–‡ç« ç±»ه‹2ن¸؛ن؛§ه“پç±»ه‹3ن¸؛ن¸‹è½½ç±»ه‹',
آ `title` varchar(50) NOT NULL,
آ `lft` int(11) NOT NULL,
آ `rgt` int(11) NOT NULL,
آ `lorder` int(11) NOT NULL COMMENT 'وژ’ه؛ڈ',
آ `create_time` int(11) NOT NULL,
آ PRIMARY KEY (`id`)
) ENGINE=InnoDBآ DEFAULT CHARSET=utf8 AUTO_INCREMENT=10 ;
--
-- ه¯¼ه‡؛è،¨ن¸çڑ„و•°وچ® `category`
--
INSERT INTO `category` (`id`, `type`, `title`, `lft`, `rgt`, `lorder`, `create_time`) VALUES
(1, 1, 'é،¶ç؛§و ڈç›®', 1, 18, 1, 1261964806),
(2, 1, 'ه…¬هڈ¸ç®€ن»‹', 14, 17, 50, 1264586212),
(3, 1, 'و–°é—»', 12, 13, 50, 1264586226),
(4, 2, 'ه…¬هڈ¸ن؛§ه“پ', 10, 11, 50, 1264586249),
(5, 1, 'èچ£èھ‰èµ„è´¨', 8, 9, 50, 1264586270),
(6, 3, '资و–™ن¸‹è½½', 6, 7, 50, 1264586295),
(7, 1, 'ن؛؛و‰چو‹›èپک', 4, 5, 50, 1264586314),
(8, 1, '留言و؟', 2, 3, 50, 1264586884),
(9, 1, 'و€»è£پ', 15, 16, 50, 1267771951);
/**
آ * وک¾ç¤؛و ‘,وٹٹو‰€وœ‰çڑ„èٹ‚点都وک¾ç¤؛ه‡؛و¥م€‚
آ * 1م€په…ˆه¾—هˆ°و ¹ç»“点çڑ„ه·¦هڈ³ه€¼ï¼ˆé»ک认و ¹èٹ‚点çڑ„titleن¸؛“é،¶ç؛§ç›®ه½•â€ï¼‰م€‚
آ * 2م€پوں¥è¯¢ه·¦هڈ³ه€¼هœ¨و ¹èٹ‚点çڑ„ه·¦هڈ³ه€¼èŒƒه›´ه†…çڑ„è®°ه½•ï¼Œه¹¶ن¸”و ¹وچ®ه·¦ه€¼وژ’ه؛ڈم€‚
آ * 3م€په¦‚وœوœ¬و¬،è®°ه½•هڈ³ه€¼ه¤§ن؛ژه‰چو¬،è®°ه½•çڑ„هڈ³ه€¼هˆ™ن¸؛هگهˆ†ç±»ï¼Œè¾“ه‡؛و—¶ه€™هٹ ç©؛و ¼م€‚
آ * @return array
آ **/
آ function display_tree(){
آ
آ آ
آ آ //èژ·ه¾—rootه·¦è¾¹ه’Œهڈ³è¾¹çڑ„ه€¼
آ آ $arr_lr = $this->category->where("title = 'é،¶ç؛§و ڈç›®'")->find();
آ آ //print_r($arr_lr);
آ آ if($arr_lr){
آ آ آ $right = array();
آ آ آ $arr_tree = $this->category->query("SELECT id, type, title, rgt FROM categoryآ WHERE lft >= ". $arr_lr['lft'] ." ANDآ lft <=".$arr_lr['rgt']." ORDER BY lft");
آ آ آ foreach($arr_tree as $v){
آ آ آ آ if(count($right)){
آ آ آ آ آ while ($right[count($right) -1] < $v['rgt']){
آ آ آ آ آ آ array_pop($right);
آ آ آ آ آ }
آ آ آ آ }
آ آ آ آ $title = $v['title'];
آ آ آ آ if(count($right)){
آ آ آ آ آ $title = '|-'.$title;
آ آ آ آ }
آ آ آ آ $arr_list[] = array('id' => $v['id'], 'type' => $type, 'title' => str_repeat(' ', count($right)).$title, 'name' =>$v['title']);
آ آ آ آ $right[]آ = $v['rgt'];
آ آ آ }
آ آ آ return $arr_list;
آ آ }
آ }
ه¥½ن؛† هڈھè¦پè؟™و ·و‰€وœ‰çڑ„هˆ†ç±»éƒ½هڈ¯ن»¥ن¸€و¬،و€§وں¥è¯¢ه‡؛و¥ن؛†ï¼Œè€Œن¸چ用é€ڑè؟‡é€’ه½’ن؛†م€‚
ن¸‹é¢çڑ„é—®é¢کوک¯و€ژو ·è؟›è،Œوڈ’ه…¥م€پهˆ 除ه’Œن؟®و”¹و“چن½œ
وڈ’ه…¥:وڈ’ه…¥و“چن½œه¾ˆç®€هچ•و‰¾هˆ°ه…¶çˆ¶èٹ‚点,ن¹‹هگژوٹٹه·¦ه€¼ه’Œهڈ³ه€¼ه¤§ن؛ژ父èٹ‚点ه·¦ه€¼çڑ„èٹ‚点çڑ„ه·¦هڈ³ه€¼هٹ ن¸ٹ2,ن¹‹هگژه†چوڈ’ه…¥وœ¬èٹ‚点,ه·¦هڈ³ه€¼هˆ†هˆ«ن¸؛父èٹ‚点ه·¦ه€¼هٹ ن¸€ه’Œهٹ ن؛Œï¼Œهڈ¯ن»¥ç”¨ن¸€ن¸ھهکه‚¨è؟‡ç¨‹و¥و“چن½œï¼ڑ
CREATEآ PROCEDURE `category_insert_by_parent`(IN pid INT,IN title VARCHAR(20), IN type INT, IN l_order INT, IN pubtime INT)
BEGIN
DECLARE myLeft INT;
آ SELECT lft into myLeft FROM category WHERE id= pid;
آ UPDATE qy_categoryآ SET rgt = rgt + 2 WHEREآ rgt > myLeft;
آ UPDATE qy_categoryآ SET lft = lft + 2 WHEREآ lft > myLeft;
آ INSERT INTO qy_category(type, title, lft, rgt, lorder, create_time) VALUES(type ,title, myLeft + 1, myLeft + 2, l_order, pubtime);
آ commit;
END
هˆ 除و“چن½œï¼ڑ
آ آ آ هˆ 除çڑ„هژںçگ†ï¼ڑ1.ه¾—هˆ°è¦پهˆ 除èٹ‚点çڑ„ه·¦هڈ³ه€¼ï¼Œه¹¶ه¾—هˆ°ن»–ن»¬çڑ„ه·®ه†چهٹ ن¸€ï¼Œ@mywidth = @rgt - @lftآ + 1;
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ 2.هˆ 除ه·¦هڈ³ه€¼هœ¨وœ¬èٹ‚点ن¹‹é—´çڑ„èٹ‚点
آ آ آ آ آ آ آ آ آ آ آ آ آ آ آ 3.ن؟®و”¹و،ن»¶ن¸؛ه¤§ن؛ژوœ¬èٹ‚点هڈ³ه€¼çڑ„و‰€وœ‰èٹ‚点,و“چن½œن¸؛وٹٹن»–ن»¬çڑ„ه·¦هڈ³ه€¼éƒ½ه‡ڈهژ»@mywidth
هکه‚¨è؟‡ç¨‹ه¦‚ن¸‹ï¼ڑ
CREATEآ PROCEDURE `category_delete_by_key`(IN id INT)
BEGIN
SELECTآ @myLeftآ :=آ lft,آ @myRightآ :=آ rgt,آ @myWidthآ :=آ rgtآ -آ lftآ +آ 1
آ آ FROMآ category
آ WHEREآ id = id;
DELETEآ FROMآ categoryآ WHEREآ lftآ BETWEENآ @myLeftآ ANDآ @myRight;
UPDATEآ nested_categoryآ SETآ rgtآ =آ rgtآ -آ @myWidthآ WHEREآ rgtآ >آ @myRight;
UPDATEآ nested_categoryآ SETآ lftآ =آ lftآ -آ @myWidthآ WHEREآ lftآ >آ @myRight;
ن؟®و”¹ï¼ڑ
è¦په‘½çڑ„ن؟®و”¹و“چن½œï¼Œوœ¬ن؛؛看ن؛†ه¾ˆن¹…ن¹ںو²،وœ‰çœ‹ه‡؛ن»€ن¹ˆè§„ه¾‹ه‡؛و¥ï¼Œهڈھè¦په‡؛و¤ن¸‹ç–,ه…ˆهˆ 除ه†چوڈ’ه…¥ï¼Œهڈھè¦پ调用ن¸ٹé¢2ن¸ھهکه‚¨è؟‡ç¨‹ه°±هڈ¯ن»¥ن؛†ï¼پ
و€»ç»“ï¼ڑوں¥è¯¢و–¹ن¾؟,ن½†وک¯ه¢هˆ و”¹و“چن½œوœ‰ç‚¹ç¹پçگگ,ن½†وک¯ن¸€èˆ¬هˆ†ç±»و¤ç±»و“چن½œن¸چوک¯ه¾ˆه¤ڑ,è؟کوک¯وں¥è¯¢ç”¨çڑ„ه¤ڑ,ه†چ说ه¼„ن¸ھهکه‚¨è؟‡ç¨‹ن¹ںو–¹ن¾؟ï¼پو— é™گهˆ†ç±»çڑ„و–¹و³•è؟کوœ‰ï¼Œن¸‹ه›ه†چن»‹ç»چ第ن؛Œç§چï¼پ









相ه…³وژ¨èچگ
ن؛Œهˆ†و³•وµپ程ه›¾1 ن؛Œهˆ†و³•وک¯ن¸€ç§چه¸¸ç”¨çڑ„و•°ه€¼è®،ç®—و–¹و³•ï¼Œç”¨ن؛ژه¯»و‰¾هچ•هڈکé‡ڈه‡½و•°çڑ„零点م€‚ه®ƒçڑ„هں؛وœ¬و€وƒ³وک¯é€ڑè؟‡ن¸چو–هœ°ه°†وگœç´¢èŒƒه›´ç¼©ه°ڈ,و¥é€¼è؟‘ه‡½و•°çڑ„零点م€‚ن¸‹é¢وˆ‘ن»¬ه°†é€ڑè؟‡وµپ程ه›¾و¥è¯¦ç»†هœ°ن»‹ç»چن؛Œهˆ†و³•çڑ„ه·¥ن½œè؟‡ç¨‹م€‚ 首ه…ˆï¼Œوˆ‘ن»¬éœ€è¦پ...
و ‡é¢کن¸çڑ„“و¸©ه؛¦è½¬وچ¢ن؛Œهˆ†و³•â€وک¯وŒ‡هœ¨ه¤„çگ†و¸©ه؛¦وµ‹é‡ڈو—¶ï¼Œé‡‡ç”¨ن؛Œهˆ†و³•و¥وں¥و‰¾و¸©ه؛¦ه¯¹ه؛”çڑ„电هژ‹وˆ–电éک»ه€¼م€‚ن؛Œهˆ†و³•ï¼Œهڈˆç§°وٹکهچٹوں¥و‰¾و³•ï¼Œوک¯ن¸€ç§چé«کو•ˆçڑ„ç®—و³•ï¼Œه¸¸ç”¨ن؛ژوœ‰ه؛ڈو•°وچ®é›†هگˆن¸ه¯»و‰¾ç‰¹ه®ڑه…ƒç´ م€‚هœ¨و¸©ه؛¦وµ‹é‡ڈ领هںں,ه¦‚وœوˆ‘ن»¬وœ‰ن¸€ن¸ھ预设çڑ„...
ن؛Œهˆ†و³•ï¼Œن¹ں称ن¸؛وٹکهچٹوگœç´¢وˆ–ن؛Œهˆ†وگœç´¢ï¼Œوک¯ن¸€ç§چهœ¨وœ‰ه؛ڈو•°ç»„ن¸وں¥و‰¾ç‰¹ه®ڑه…ƒç´ çڑ„وگœç´¢ç®—و³•م€‚è؟™ن¸ھو–¹و³•çڑ„و ¸ه؟ƒو€وƒ³وک¯é€ڑè؟‡ن¸چو–ه°†وگœç´¢هŒ؛é—´ه‡ڈهچٹ,و¥ه؟«é€ںه®ڑن½چç›®و ‡ه€¼çڑ„ن½چç½®م€‚ن؛Œهˆ†و³•هœ¨ن؟،وپ¯وٹ€وœ¯م€پو•°وچ®ه¤„çگ†ه’Œç®—و³•è®¾è®،ç‰é¢†هںںوœ‰ç€ه¹؟و³›çڑ„ه؛”用...
ن؛Œهˆ†و³•ï¼Œن¹ں称ن¸؛وٹکهچٹوگœç´¢وˆ–ن؛Œهˆ†وگœç´¢ï¼Œوک¯ن¸€ç§چهœ¨وœ‰ه؛ڈو•°ç»„ن¸وں¥و‰¾ç‰¹ه®ڑه…ƒç´ çڑ„وگœç´¢ç®—و³•م€‚è؟™ن¸ھو–¹و³•çڑ„ه…³é”®هœ¨ن؛ژه…¶é«کو•ˆو€§ï¼Œو¯ڈو¬،وں¥è¯¢éƒ½èƒ½ه°†وگœç´¢...و¤ه¤–,ه®é™…ه؛”用ن¸هڈ¯èƒ½éœ€è¦پ考虑ه¼‚ه¸¸ه¤„çگ†ï¼Œو¯”ه¦‚ه½“هŒ؛é—´و— و³•ه†چ细هˆ†و—¶ï¼Œéک²و¢و— é™گه¾ھçژ¯م€‚
ن؛Œهˆ†و³•(dichotomie) هچ³ن¸€هˆ†ن¸؛ن؛Œçڑ„و–¹و³•. 设[a,b]ن¸؛Rçڑ„é—هŒ؛é—´. é€گو¬،ن؛Œهˆ†و³•ه°±وک¯é€ ه‡؛ه¦‚ن¸‹çڑ„هŒ؛é—´ه؛ڈهˆ—([an,bn]):a0=a,b0=b,ن¸”ه¯¹ن»»ن¸€è‡ھ然و•°n,[an+1,bn+1]وˆ–者ç‰ن؛ژ[an,cn],وˆ–者ç‰ن؛ژ[cn,bn],ه…¶ن¸cnè،¨ç¤؛[an,bn]çڑ„...
و ¹وچ®ç»™ه®ڑçڑ„و–‡ن»¶ن؟،وپ¯ï¼Œوˆ‘ن»¬هڈ¯ن»¥و€»ç»“ه‡؛ن»¥ن¸‹ه…³ن؛ژ“ن؛Œهˆ†و³•وژ’ه؛ڈç®—و³•Cè¯è¨€ه®çژ°â€çڑ„相ه…³çں¥è¯†ç‚¹ï¼ڑ ### 1. ن؛Œهˆ†و³•وگœç´¢ç®—و³•هژںçگ† ن؛Œهˆ†و³•وگœç´¢ç®—و³•ï¼Œن¹ں称ن¸؛وٹکهچٹوں¥و‰¾ç®—و³•ï¼Œوک¯ن¸€ç§چهœ¨وœ‰ه؛ڈو•°ç»„ن¸وں¥و‰¾ç‰¹ه®ڑه…ƒç´ çڑ„وگœç´¢ç®—و³•م€‚ه…¶هں؛وœ¬و€وƒ³...
هˆ©ç”¨javaن؛Œهˆ†و³•و¥è®،ç®—وœ€é è؟‘ه€¼,é€ڑè؟‡ن؛Œهˆ†و³•و¥éپچهژ†و•°وچ®ï¼Œه¾—هˆ°وƒ³è¦پوœ€è؟‘ه€¼
ن؛Œهˆ†و³•çڑ„ن½؟用 ن؛Œهˆ†و³•وک¯ن¸€ç§چه¸¸ç”¨çڑ„و•°ه€¼è®،ç®—و–¹و³•ï¼Œç”¨ن؛ژو‰¾هˆ°ه‡½و•°çڑ„零点وˆ–وپه€¼م€‚هœ¨è®،ç®—وœ؛科ه¦ن¸ï¼Œن؛Œهˆ†و³•وک¯è§£ه†³ç›´é™…é—®é¢کçڑ„é‡چè¦په·¥ه…·م€‚ن¸‹é¢وˆ‘ن»¬ه°†è¯¦ç»†ن»‹ç»چن؛Œهˆ†و³•çڑ„ن½؟用ه’Œه®è·µم€‚ ن؛Œهˆ†و³•çڑ„ه®ڑن¹‰ ن؛Œهˆ†و³•وک¯ن¸€ç§چو•°ه€¼è®،ç®—و–¹و³•ï¼Œ...
- **éپ؟ه…چو— é™گه¾ھçژ¯**ï¼ڑ设ه®ڑوœ€ه¤§è؟ن»£و¬،و•°وˆ–وœ€ه°ڈهŒ؛é—´é•؟ه؛¦ن»¥éک²و¢و— é™گه¾ھçژ¯م€‚ - **و”¹è؟›ن¸ç‚¹é€‰و‹©**ï¼ڑوœ‰و—¶هڈ¯ن»¥é€ڑè؟‡é€‰و‹©هŒ؛间端点çڑ„هٹ وƒه¹³ه‡ه€¼وˆ–ه…¶ن»–ç–ç•¥و¥و”¹ه–„ن¸ç‚¹é€‰و‹©ï¼Œن»¥و›´ه¥½هœ°é€¼è؟‘零点م€‚ - **误ه·®هˆ†وگ**ï¼ڑçگ†è§£ه¹¶وژ§هˆ¶ç®—و³•çڑ„...
ن؛Œهˆ†و³•ï¼Œن¹ں称ن¸؛وٹکهچٹوگœç´¢ï¼Œوک¯ن¸€ç§چهœ¨وœ‰ه؛ڈو•°ç»„ن¸وں¥و‰¾ç‰¹ه®ڑه…ƒç´ çڑ„وگœç´¢ç®—و³•م€‚ه®ƒé€ڑè؟‡ن¸چو–ه°†وں¥و‰¾هŒ؛é—´ه‡ڈهچٹ,ه؟«é€ںه®ڑن½چç›®و ‡ه€¼م€‚هœ¨و•°ه€¼هˆ†وگ领هںں,ن؛Œهˆ†و³•ن¹ں被用ن؛ژو±‚解و–¹ç¨‹ï¼Œç‰¹هˆ«وک¯è؟ç»ه‡½و•°çڑ„零点م€‚هœ¨وœ¬و،ˆن¾‹ن¸ï¼Œوˆ‘ن»¬ه°†وژ¢è®¨ه¦‚ن½•ç”¨...
ن؛Œهˆ†و³•ï¼Œن¹ں称ن¸؛وٹکهچٹوگœç´¢وˆ–هŒ؛é—´وگœç´¢ï¼Œوک¯ن¸€ç§چهœ¨وœ‰ه؛ڈه؛ڈهˆ—ن¸وں¥و‰¾ç‰¹ه®ڑه…ƒç´ çڑ„وگœç´¢ç®—و³•م€‚ه®ƒé€ڑè؟‡ن¸چو–ه°†وگœç´¢èŒƒه›´ه‡ڈهچٹو¥é€¼è؟‘ç›®و ‡ه€¼ï¼Œé€‚用ن؛ژ解ه†³ç‰¹ه®ڑç±»ه‹çڑ„و•°ه¦é—®é¢ک,ه¦‚ه¯»و‰¾è؟ç»ه‡½و•°çڑ„零点م€‚هœ¨وœ¬هœ؛و™¯ن¸ï¼Œوˆ‘ن»¬ه°†وژ¢è®¨ه¦‚ن½•è؟گ用...
ن؛Œهˆ†و³•
وœ¬ن¾‹ه®çژ°ن؛†ç”¨cè¯è¨€ه®çژ°ن؛†ن؛Œهˆ†و³•و±‚解و–¹ç¨‹م€‚وœ¬ن¾‹ن¸»è¦پن»‹ç»چ用ن؛Œهˆ†و³•و±‚解و–¹ç¨‹f(X)=sin(x)هœ¨(-3,7)è؟™ن¸ھ范ه›´ه†…çڑ„解Cè¯è¨€ه®çژ°و–¹و³•م€‚ و±‚解ن¸»è¦پé€ڑè؟‡ه‡½و•°BisectRoot()و¥ه®Œوˆگم€‚该ه‡½و•°é¦–ه…ˆو ¹وچ®ن؛Œهˆ†و³•çڑ„需è¦پو‰«وڈڈو ¹çڑ„هکهœ¨ هڈٹو ¹çڑ„...
ن؛Œهˆ†و³•è®،ç®—و–¹و³•هڈٹVB编程ن»£ç پ设è®، ن؛Œهˆ†و³•وک¯ن¸€ç§چه¸¸ç”¨çڑ„و•°ه€¼هˆ†وگو–¹و³•ï¼Œç”¨و¥و±‚解éç؛؟و€§و–¹ç¨‹çڑ„و ¹م€‚ه…¶هں؛وœ¬و€وƒ³وک¯ه°†وگœç´¢هŒ؛é—´ن¸چو–هœ°ç¼©ه°ڈ,直هˆ°و‰¾هˆ°و ¹و‰€هœ¨çڑ„ن½چç½®م€‚ن؛Œهˆ†و³•çڑ„ن¼ک点وک¯è®،ç®—é€ںه؛¦ه؟«م€پç²¾ه؛¦é«ک,ن½†éœ€è¦پوگœç´¢هŒ؛é—´çڑ„هˆه€¼ç¦»...
ن؛Œهˆ†و³•ï¼Œن¹ں称ن¸؛وٹکهچٹوں¥و‰¾و³•وˆ–هŒ؛é—´وگœç´¢و³•ï¼Œوک¯ن¸€ç§چهœ¨وœ‰ه؛ڈو•°وچ®é›†هگˆن¸ه¯»و‰¾ç‰¹ه®ڑه…ƒç´ çڑ„ç®—و³•م€‚هœ¨MATLABن¸ï¼Œن؛Œهˆ†و³•é€ڑه¸¸ç”¨ن؛ژو•°ه€¼è®،算,ه¦‚و±‚解و–¹ç¨‹çڑ„و ¹م€پوں¥و‰¾و•°ç»„ن¸çڑ„特ه®ڑه€¼وˆ–者ن¼کهŒ–é—®é¢کم€‚ن¸‹é¢ه°†è¯¦ç»†è®¨è®؛ن¸‰ç§چن¸چهگŒçڑ„ن؛Œهˆ†و³•MATLAB...
éڑڈهگژ,è؟›ه…¥ن¸€ن¸ھو— é™گه¾ھçژ¯ï¼Œç”¨ن؛ژن¸چو–缩ه°ڈوگœç´¢هŒ؛é—´ç›´هˆ°و‰¾هˆ°é›¶ç‚¹وˆ–و»،足终و¢و،ن»¶م€‚ - ه¦‚وœ `f(x1)` وˆ– `f(x2)` çڑ„ه€¼ن¸؛零,هˆ™و‰¾هˆ°ن؛†ن¸€ن¸ھ零点,ه¹¶ه°†ç»“وœè¾“ه‡؛م€‚ - ه¦‚وœ `f(x1) * f(x2) > 0`,هˆ™è،¨وکژه‡½و•°هœ¨[a, b]هŒ؛é—´ه†…و²،وœ‰...
简هچ•çڑ„هپڑن؛†ن¸€ن¸ھن؛Œهˆ†و³•çڑ„ç®—و³•ï¼Œه°ڈن؛ژوںگن¸ھ特ه®ڑه€¼هگژهپœو¢è؟گè،Œم€‚
ن؛Œهˆ†و³•ï¼Œهڈˆç§°وٹکهچٹوگœç´¢و³•ï¼Œوک¯ن¸€ç§چهœ¨وœ‰ه؛ڈو•°ç»„ن¸وں¥و‰¾ç‰¹ه®ڑه…ƒç´ çڑ„وگœç´¢ç®—و³•م€‚ه®ƒن»¥ه…¶é«کو•ˆçڑ„و€§èƒ½هœ¨è®،ç®—و–¹و³•ن¸هچ وچ®é‡چè¦پهœ°ن½چ,特هˆ«وک¯هœ¨è§£ه†³و•°ه€¼è®،ç®—é—®é¢کو—¶ï¼Œه¦‚و±‚解و–¹ç¨‹çڑ„و ¹م€پن¼کهŒ–é—®é¢که’Œوگœç´¢ç‰¹ه®ڑه€¼م€‚هœ¨VC++6.0çژ¯ه¢ƒن¸‹ه®çژ°ن؛Œهˆ†و³•...
هœ¨VB(Visual Basic)编程è¯è¨€ن¸ï¼Œن؛Œهˆ†و³•وک¯ن¸€ç§چç»ڈه…¸çڑ„و•°ه€¼و–¹و³•ï¼Œç”¨ن؛ژه¯»و‰¾هچ•هڈکé‡ڈو–¹ç¨‹çڑ„ه®و•°و ¹م€‚è؟™ç§چو–¹و³•é€‚用ن؛ژè؟ç»ه‡½و•°ï¼Œه¹¶ن¸”هœ¨ç»™ه®ڑçڑ„هŒ؛é—´ه†…ه·²çں¥ه‡½و•°ه€¼و”¹هڈک符هڈ·م€‚ن»¥ن¸‹وک¯ه¯¹ن؛Œهˆ†و³•هڈٹه…¶هœ¨VBن¸ه®çژ°çڑ„详细解é‡ٹم€‚ 首ه…ˆï¼Œ...
وژ¥ن¸‹و¥ï¼Œè؟›ه…¥ن¸€ن¸ھو— é™گه¾ھçژ¯ï¼Œه¾ھçژ¯ن½“ه†…部ه®çژ°ن؛†ن؛Œهˆ†و³•çڑ„و ¸ه؟ƒé€»è¾‘ï¼ڑ 1. 首ه…ˆè®،ç®—ه½“ه‰چهŒ؛é—´çڑ„ن¸ç‚¹x = (a+b)/2م€‚ 2. 然هگژè®،ç®—xن»£ه…¥و–¹ç¨‹هگژçڑ„结وœy = x^3 + 4x^2 - 10م€‚ 3. و£€وں¥yوک¯هگ¦è¶³ه¤ںوژ¥è؟‘零(هچ³|y| ),若و»،足و،ن»¶هˆ™...