似然函数的理解

在数理统计学中，似然函数是一种关于统计模型中的参数的函数，表示模型参数中的似然性。似然函数在统计推断中有重大作用，如在最大似然估计和费雪信息之中的应用等等。“似然性”与“或然性”或“概率”意思相近，都是指某种事件发生的可能性，但是在统计学中，“似然性”和“或然性”或“概率”又有明确的区分。概率用于在已知一些参数的情况下，预测接下来的观测所得到的结果，而似然性则是用于在已知某些观测所得到的结果时，对有关事物的性质的参数进行估计。

在这种意义上，似然函数可以理解为条件概率的逆反。在已知某个参数B时，事件A会发生的概率写作。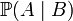

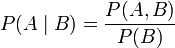
利用贝叶斯定理，

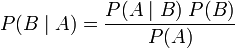
因此，我们可以反过来构造表示似然性的方法：已知有事件A发生，运用似然函数，我们估计参数B的可能性。形式上，似然函数也是一种条件概率函数，但我们关注的变量改变了：

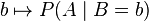
注意到这里并不要求似然函数满足归一性：。一个似然函数乘以一个正的常数之后仍然是似然函数。对所有α > 0，都可以有似然函数：

例子

两次投掷都正面朝上时的似然函数

考虑投掷一枚硬币的实验。通常来说，已知投出的硬币正面朝上和反面朝上的概率各自是p_H = 0.5，便可以知道投掷若干次后出现各种结果的可能性。比如说，投两次都是正面朝上的概率是0.25。用条件概率表示，就是：

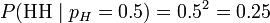
其中H表示正面朝上。

在统计学中，我们关心的是在已知一系列投掷的结果时，关于硬币投掷时正面朝上的可能性的信息。我们可以建立一个统计模型：假设硬币投出时会有p_H 的概率正面朝上，而有1 − p_H 的概率反面朝上。这时，条件概率可以改写成似然函数：

也就是说，对于取定的似然函数，在观测到两次投掷都是正面朝上时，p_H = 0.5 的似然性是0.25（这并不表示当观测到两次正面朝上时p_H = 0.5 的概率是0.25）。

如果考虑p_H = 0.6，那么似然函数的值也会改变。

三次投掷中头两次正面朝上，第三次反面朝上时的似然函数

注意到似然函数的值变大了。这说明，如果参数p_H 的取值变成0.6的话，结果观测到连续两次正面朝上的概率要比假设p_H = 0.5 时更大。也就是说，参数p_H 取成0.6 要比取成0.5 更有说服力，更为“合理”。总之，似然函数的重要性不是它的具体取值，而是当参数变化时函数到底变小还是变大。对同一个似然函数，如果存在一个参数值，使得它的函数值达到最大的话，那么这个值就是最为“合理”的参数值。

在这个例子中，似然函数实际上等于：

， 其中。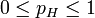

如果取p_H = 1，那么似然函数达到最大值1。也就是说，当连续观测到两次正面朝上时，假设硬币投掷时正面朝上的概率为1是最合理的。

类似地，如果观测到的是三次投掷硬币，头两次正面朝上，第三次反面朝上，那么似然函数将会是：

， 其中T表示反面朝上，。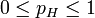

这时候，似然函数的最大值将会在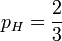的时候取到。也就是说，当观测到三次投掷中前两次正面朝上而后一次反面朝上时，估计硬币投掷时正面朝上的概率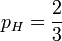是最合理的。

 应用

最大似然估计

最大似然估计是似然函数最初也是最自然的应用。上文已经提到，似然函数取得最大值表示相应的参数能够使得统计模型最为合理。从这样一个想法出发，最大似然估计的做法是：首先选取似然函数（一般是概率密度函数或概率质量函数），整理之后求最大值。实际应用中一般会取似然函数的对数作为求最大值的函数，这样求出的最大值和直接求最大值得到的结果是相同的。似然函数的最大值不一定唯一，也不一定存在。与矩法估计比较，最大似然估计的精确度较高，信息损失较少，但计算量较大。

似然比检验

似然比检验是利用似然函数来检测某个假设（或限制）是否有效的一种检验。一般情况下，要检测某个附加的参数限制是否是正确的，可以将加入附加限制条件的较复杂模型的似然函数最大值与之前的较简单模型的似然函数最大值进行比较。如果参数限制是正确的，那么加入这样一个参数应当不会造成似然函数最大值的大幅变动。一般使用两者的比例来进行比较。尼曼-皮尔森引理说明，似然比检验是所有具有同等显著性差异的检验中最有统计效力的检验。