Slope One is a family of algorithms used for collaborative filtering, introduced in a 2005 paper by Daniel Lemire and Anna Maclachlan[1]. Arguably, it is the simplest form of non-trivial item-based collaborative filtering based on ratings. Their simplicity makes it especially easy to implement them efficiently while their accuracy is often on par with more complicated and computationally expensive algorithms[1][2]. They have also been used as building blocks to improve other algorithms[3][4][5][6][7][8].
[edit]Item-based collaborative filtering of rated resources and overfitting
When ratings of items are available, such as is the case when people are given the option of ratings resources (between 1 and 5, for example), collaborative filtering aims to predict the ratings of one individual based on his past ratings and on a (large) database of ratings contributed by other users.
Example: Can we predict the rating an individual would give to the new Celine Dion album given that he gave the Beatles 5 out of 5?
In this context, item-based collaborative filtering [9][10] predicts the ratings on one item based on the ratings on another item, typically using linear regression (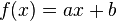 ). Hence, if there are 1,000 items, there could be up to 1,000,000 linear regressions to be learned, and so, up to 2,000,000 regressors. This approach may suffer from severe overfitting[1] unless we select only the pairs of items for which several users have rated both items.
). Hence, if there are 1,000 items, there could be up to 1,000,000 linear regressions to be learned, and so, up to 2,000,000 regressors. This approach may suffer from severe overfitting[1] unless we select only the pairs of items for which several users have rated both items.
A better alternative may be to learn a simpler predictor such as 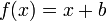 : experiments show that this simpler predictor (called Slope One) sometimes outperforms[1] linear regression while having half the number of regressors. This simplified approach also reduces storage requirements and latency.
: experiments show that this simpler predictor (called Slope One) sometimes outperforms[1] linear regression while having half the number of regressors. This simplified approach also reduces storage requirements and latency.
Item-based collaborative is just one form of collaborative filtering. Other alternatives include user-based collaborative filtering where relationships between users are of interest, instead. However, item-based collaborative filtering is especially scalable with respect to the number of users.
[edit]Item-based collaborative filtering of purchase statistics
We are not always given ratings: when the users provide only binary data (the item was purchased or not), then Slope One and other rating-based algorithm do not apply. Examples of binary item-based collaborative filtering include Amazon's item-to-item patented algorithm[11] which computes the cosine between binary vectors representing the purchases in a user-item matrix.
Being arguably simpler than even Slope One, the Item-to-Item algorithm offers an interesting point of reference. Let us consider an example.
Sample purchase statistics
Customer
Item 1
Item 2
Item 3
| John |
Bought it |
Didn't buy it |
Bought it |
| Mark |
Didn't buy it |
Bought it |
Bought it |
| Lucy |
Didn't buy it |
Bought it |
Didn't buy it |
In this case, the cosine between items 1 and 2 is:
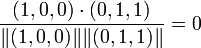 ,
,
The cosine between items 1 and 3 is:
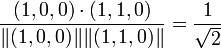 ,
,
Whereas the cosine between items 2 and 3 is:
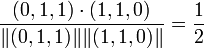 .
.
Hence, a user visiting item 1 would receive item 3 as a recommendation, a user visiting item 2 would receive item 3 as a recommendation, and finally, a user visiting item 3 would receive item 1 (and then item 2) as a recommendation. The model uses a single parameter per pair of item (the cosine) to make the recommendation. Hence, if there are n items, up to n(n-1)/2 cosines need to be computed and stored.
[edit]Slope one collaborative filtering for rated resources
To drastically reduce overfitting, improve performance and ease implementation, the Slope One family of easily implemented Item-based Rating-Basedcollaborative filtering algorithms was proposed. Essentially, instead of using linear regression from one item's ratings to another item's ratings (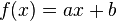 ), it uses a simpler form of regression with a single free parameter (
), it uses a simpler form of regression with a single free parameter (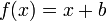 ). The free parameter is then simply the average difference between the two items' ratings. It was shown to be much more accurate than linear regression in some instances[1], and it takes half the storage or less.
). The free parameter is then simply the average difference between the two items' ratings. It was shown to be much more accurate than linear regression in some instances[1], and it takes half the storage or less.
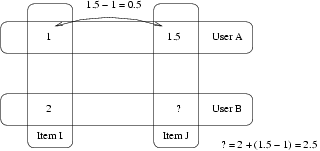
Example:
- User A gave a 1 to Item I and an 1.5 to Item J.
- User B gave a 2 to Item I.
- How do you think User B rated Item J?
- The Slope One answer is to say 2.5 (1.5-1+2=2.5).
For a more realistic example, consider the following table.
Sample rating database
Customer
Item 1
Item 2
Item 3
| John |
5 |
3 |
2 |
| Mark |
3 |
4 |
Didn't rate it |
| Lucy |
Didn't rate it |
2 |
5 |
In this case, the average difference in ratings between item 2 and 1 is (2+(-1))/2=0.5. Hence, on average, item 1 is rated above item 2 by 0.5. Similarly, the average difference between item 3 and 1 is 3. Hence, if we attempt to predict the rating of Lucy for item 1 using her rating for item 2, we get 2+0.5 = 2.5. Similarly, if we try to predict her rating for item 1 using her rating of item 3, we get 5+3=8.
If a user rated several items, the predictions are simply combined using a weighted average where a good choice for the weight is the number of users having rated both items. In the above example, we would predict the following rating for Lucy on item 1:
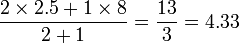
Hence, given n items, to implement Slope One, all that is needed is to compute and store the average differences and the number of common ratings for each of the n2 pairs of items.
[edit]Algorithmic complexity of Slope One
Suppose there are n items, m users, and N ratings. Computing the average rating differences for each pair of items requires up to n(n-1)/2 units of storage, and up to m n2 time steps. This computational bound may be pessimistic: if we assume that users have rated up to y items, then it is possible to compute the differences in no more than n2+my2. If a user has entered x ratings, predicting a single rating requires x time steps, and predicting all of his missing ratings requires up to (n-x)x time steps. Updating the database when a user has already entered x ratings, and enters a new one, requires xtime steps.
It is possible to reduce storage requirements by partitioning the data (see Partition (database)) or by using sparse storage: pairs of items having no (or few) corating users can be omitted.
from:http://en.wikipedia.org/wiki/Slope_One#Open_source_software_implementing_Slope_One





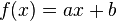 ). Hence, if there are 1,000 items, there could be up to 1,000,000 linear regressions to be learned, and so, up to 2,000,000 regressors. This approach may suffer from severe
). Hence, if there are 1,000 items, there could be up to 1,000,000 linear regressions to be learned, and so, up to 2,000,000 regressors. This approach may suffer from severe 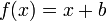 : experiments show that this simpler predictor (called Slope One) sometimes outperforms
: experiments show that this simpler predictor (called Slope One) sometimes outperforms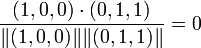 ,
,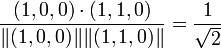 ,
,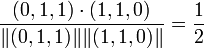 .
.
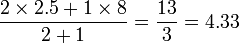



相关推荐
加权SlopeOne算法是协同过滤推荐系统中的一种优化策略,旨在解决原始SlopeOne算法在处理大规模数据集时存在的问题。协同过滤是推荐系统中最常见的技术之一,它基于用户的历史行为来预测他们可能对未评价物品的兴趣。...
根据提供的文件信息,本文将详细解析“基于Slope One算法的电影推荐系统”的核心知识点,包括Slope One算法的基本原理、实现步骤以及在电影推荐系统中的应用等方面。 ### Slope One算法简介 Slope One算法是一种...
在描述中提到的博文链接虽然缺失,但通常这类博客会详细介绍SlopeOne算法的原理,以及如何将其与大数据技术结合。 首先,让我们详细了解一下Slope One算法。它主要包括两个步骤:预处理(Preprocessing)和预测...
SlopeOne算法是一种基于协同过滤的简单预测方法,主要用于推荐系统。它由Daniel Lemire在2005年提出,其核心思想是通过计算用户之间的相似度,来预测用户对未评分项目的评分。这种算法相对高效,适用于处理大规模...
程序以matlab语言编写,包括了Pearson相似度、UserCF、ItemCF、slope one算法、TopN推荐、MAE、RMSE、准确度、覆盖率等常用算法代码.zip数学建模大赛赛题、解决方案资料,供备赛者学习参考!数学建模大赛赛题、解决...
程序以matlab语言编写,包括了Pearson相似度、UserCF、ItemCF、slopeone算法
融合改进加权 Slope One 的协同过滤算法 在个性化推荐系统中,协同过滤算法是其中最流行和最有效的方法之一。但是,数据稀疏性问题对传统协同过滤算法的应用造成了很大的挑战。在数据极端稀疏的情况下,用户已评分...
【Slope One 算法】Slope One算法是一种基于协同过滤的推荐系统方法,它依赖于简单的线性回归模型来预测用户对未评分项的评分。算法的核心思想是通过计算用户对已评分项目的评分差值(即斜率)来预测用户对未评分...
Slope One算法是一种用于在线评分推荐系统的协同过滤算法。它通过利用用户对已有物品的评分,来预测用户对未知物品的可能评分。Slope One算法的核心思想是,预先计算出不同物品之间评分的平均差异,这些差异来源于...
在大数据和个性化推荐系统领域,SlopeOne算法是一种简单而有效的预测方法,尤其适用于处理大规模数据集。它由Daniel Lemire等人在2005年提出,旨在通过用户对物品的评分差异进行预测,以实现精准的推荐。在Ruby编程...
class SlopeOne { private $ratings; public function __construct($data) { // 初始化评分矩阵 $this->ratings = $data; } public function predict($userId, $itemId) { // 计算斜率和预测评分的逻辑 } ...
针对Slope One算法存在预测精度依赖于用户对待预测项目的评分数量的缺陷,提出了一种基于项目属性相似度和MapReduce并行化的Slope One算法.首先计算项目间的属性相似度,并将其与Slope One算法相融合以提高预测精度...