浅谈大数的进制转换

在数据结构课关于栈的这一章中，我们都学过用“模2取余法”来将一个10进制数转换为一个二进制数，进而可以推广到“模n取余法”，经其转换为n进制（n任意指定）。

确实，这是一个很基础的题目，可你是否想过如果这个10进制数是一个大数（其位数可能上千位，此时用一般数据类型肯定是会溢出的），那么这个问题又如何来求解呢？

当然，也许你会说很简单嘛，自己写一个大数类（当然至少要写一个大数除法才行），或者你用的是Java这种现代化语言，就更轻松了，直接用BigInteger这样的大数类就可以来表示一个大数，进而用书上教的方法来实现。

但是，真的需要用到大数类吗？事实上，“杀鸡焉用牛刀“，我们在纸上模拟一番上述运算后就可以发现，只要做一些小小的改进，就可以在不使用大数的情况下，也可以通过“模n取余”的原理来实现大数的进制转换的。（当然，整体的思想仍然是“模n取余”原理！！！）。

举个简单的例子，就比如说把10进制数12转换为2进制形式，书上的方法可以用下图来表示

按照 “先余为低位，后余为高位“这条铁律，其结果为1100.

这是书上教我们的常规思路（可惜按这个的话，大数是没法考虑的，因为假如这里不是12，而是一个1000位的大数，由于是是对大数的整体进行取余运算，不使用大数类及其除法操作，又如何得以进行呢？），可我们的目的是不使用大数类，那么现在我们就来换一个视角来看这个问题，12是一个十位数，十位上是1，个位上是2，按照我们正常的思维来看，这个计算应该是下面这样的：

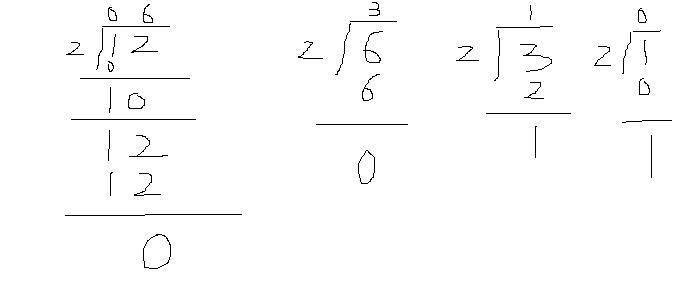
那么我们发现在第一轮运算时，十位上的1作为被除数，2作为除数，得到的商是0，余数是1(可以断言只考虑当前这一个数位的计算，余数或是0，或是1，若是1的话，则进入下一数位（这里即对个位进行运算）时，要用1乘上进制（这里是10）再加上下一个数位上的值（这里是2）)，即得到运算进入个位时被除数是12，除数是2，得到的商是6，余数是0。第一轮运算的结果是商是06，余数是0.

进入第二轮运算，则上一轮的商6（这里首先要去掉前面多余的0）变成本轮的被除数，如此下去，即可得到每轮的余数。

推广开来，如果被除数是一个1000位的大数，例如“12343435154324123……342314324343”

那么我们照样可以从第一个数位开始逐位考虑，比如第一位是1（作为被除数），2是除数，得到的商是0，余数是1，然后是第二个数位2，由于上一位留下了余数1，则此时被除数应该是1*10+2 = 12,所以得到的商是6，余数是0，即运算到此时的商是06，然后是第三个数位3，由于上一个数位留下的余数是0，所以此时被除数就是3，。。。如此下去就完成第一轮的运算，

这一轮完毕后，需要把得到的商变成下一轮的被除数，继续上述的运算，直到被除数为0才停止。

下面给出了一个示例代码，展示了如何将一个10进制的大数转换为其二进制形式，仅供参考：

<!--<br /><br />Code highlighting produced by Actipro CodeHighlighter (freeware)<br />http://www.CodeHighlighter.com/<br /><br />-->#include<stdio.h>
#include<string.h>

charstr[1000];//输入字符串
intstart[1000],ans[1000],res[1000];//被除数，商，余数

//转换前后的进制
constintoldBase=10;
constintnewBase=2;

voidchange()
{//各个数位还原为数字形式
inti,len=strlen(str);
start[0]=len;
for(i=1;i<=len;i++)
{
if(str[i-1]>='0'&&str[i-1]<='9')
{
start[i]=str[i-1]-'0';
}
}
}

voidsolve()
{
memset(res,0,sizeof(res));//余数初始化为空
inty,i,j;
//模n取余法，(总体规律是先余为低位，后余为高位)
while(start[0]>=1)
{//只要被除数仍然大于等于1，那就继续“模2取余”
y=0;
i=1;
ans[0]=start[0];
//
while(i<=start[0])
{
y=y*oldBase+start[i];
ans[i++]=y/newBase;
y%=newBase;
}
res[++res[0]]=y;//这一轮运算得到的余数
i=1;
//找到下一轮商的起始处
while((i<=ans[0])&&(ans[i]==0))i++;
//清除这一轮使用的被除数
memset(start,0,sizeof(start));
//本轮得到的商变为下一轮的被除数
for(j=i;j<=ans[0];j++)
start[++start[0]]=ans[j];
memset(ans,0,sizeof(ans));//清除这一轮的商，为下一轮运算做准备
}
}

voidoutput()
{//从高位到低位逆序输出
inti;
for(i=res[0];i>=1;--i)
{
printf("%d",res[i]);
}
printf("/n");
}

intmain()
{
scanf("%s",str);
change();
solve();
output();
return 0;
}

当然，这个思路可以推广为“m进制的大数转换为n进制形式“，这就留给你自行思考吧…

记住一点，不要把被除数当做一个数字，而应该视为一个字符串，逐位来做除法。我举个简单例子1001（有两个连续0，其实无所谓什么数值，因为这里根本只一位一位地来做除法），每一轮运算都对被除数从左到右，一位一位地来做。先是第一轮此时被除数是1001，有4位，先做第一位，也就是1，1除以2得到局部商是0，余数是1，再做第二位，也就是0，此时由于上一位1做运算留下了个余数1，所以此时的被除数就不仅仅是当前位0了，而应该是1*10+0 = 10，也就是说在做某一位的运算时要考虑前一位余下的余数，若前一位余下的余数是1，则要乘以进制（这里是10进制）再加上当前位，好了，现在的被除数就是10，那么得到的局部商是5，余数是0.再来做第三位0，由于上一位的余数是0，所以此时的被除数就是当前位0，则得到的局部商是0，余数是0。最后来到第四位1，由于上一位余数是0，所以此时被除数就是当前位1，得到的局部商是0，余数是1.由于已经从左到右扫描一遍了，则第一轮运算结束，最后得到的余数1就是最终结果的最低位，并且这一轮得到的商是0500，我们可以做处理（去掉前面的连续0，最后得到本轮的商是500）。最后把这一轮的商500作为下一轮的被除数。继续上述运算。

这里我就只解释第一轮的细节了，其他轮次过程同上，仅仅是被除数不同而已。

如果你对这个话题感兴趣的话，可以用这个思路来尝试解决下PKU 1220这个题目：http://acm.pku.edu.cn/JudgeOnline/problem?id=

作者：phinecos(洞庭散人)
出处：http://phinecos.cnblogs.com/
本文版权归作者和博客园共有，欢迎转载，但请保留此段声明，并在文章页面明显位置给出原文连接