在数学中,数量积(也称为标量积、点积、点乘)是接受在实数R上的两个矢量并返回一个实数值标量的二元运算。它是欧几里得空间的标准内积。
计算方法
两个矢量a = [a1, a2,…, an]和b = [b1, b2,…, bn]的点积定义为:
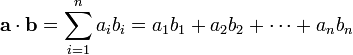
这里的Σ指示总和符号。
例如,两个三维矢量[1, 3, −5]和[4, −2, −1]的点积是
 。
。
使用矩阵乘法并把(纵列)矢量当作n×1 矩阵,点积还可以写为:
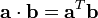 ,
,
这里的aT指示矩阵a的转置。
使用上面的例子,将一个1×3矩阵(就是行矢量)乘以一个3×1矢量得到结果(通过矩阵乘法的优势得到1×1矩阵也就是标量):
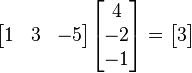 。
。
几何解释
在欧几里得空间中,点积可以直观地定义为
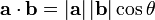 ,
,
这里 |x| 表示x的范数(长度),θ表示两个矢量之间的角度。
注意:点积的形式定义和这个定义不同;在形式定义中,a和b的夹角是通过上述等式定义的。
这样,两个互相垂直的矢量的点积总是零。若a和b都是单位矢量(长度为1),它们的点积就是它们的夹角的余弦。那么,给定两个矢量,它们之间的夹角可以通过下列公式得到:
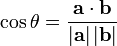
这个运算可以简单地理解为:在点积运算中,第一个矢量投影到第二个矢量上(这里,矢量的顺序是不重要的,点积运算是可交换的),然后通过除以它们的标量长度来“标准化”。这样,这个分数一定是小于等于1的,可以简单地转化成一个角度值。
来源于: http://zh.wikipedia.org/wiki/%E7%82%B9%E7%A7%AF
分享到:






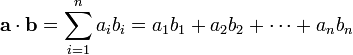
 。
。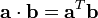 ,
,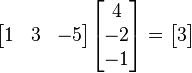 。
。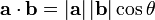 ,
,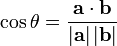



相关推荐
向量的数量积,也称为点积或内积,是两个向量的一种运算,结果是一个实数。它的几何意义可以通过向量在某轴上的投影来定义。具体来说,一个向量在另一个向量上的投影指的是从原点出发沿一个向量方向画一条线段,这条...
数量积也称为点积、内积,记作 a · b,它是一个标量,表示两个向量的方向 cosine 值乘以它们的模长积。数量积的定义式为: a · b = |a| |b| cosθ 其中,a 和 b 是两个向量,θ 是它们之间的夹角。 数量积的...
在这一领域中,向量的数量积(点积)和向量积(叉积)是两种常见的运算形式,它们各自有着不同的几何意义和物理应用。 首先,让我们来探讨向量的数量积。数量积是指两个向量的模长和它们夹角余弦的乘积,它反映的是...
我们可以通过设定适当的变量,如E点相对于A点的距离,然后利用向量的线性组合和数量积的性质,来表达DE·CB,并找出其最大值。 总的来说,理解和熟练运用平面向量的数量积是解决高中数学中涉及向量问题的关键。通过...
向量数量积 首先输入向量维数 然后输入两个向量的坐标 最后评价程序
《平面向量的数量积》是高中数学中的核心概念,它涉及了代数、几何和三角函数的融合,是解决实际问题的重要工具。本教学设计旨在深入解析这一概念,引导学生理解其物理背景、数学定义、几何意义以及相关性质和运算...
首先,向量的数量积,也称为点积,是一个标量值,表示两个向量的大小和方向的综合效应。对于两个二维平面向量 a = (x1, y1) 和 b = (x2, y2),它们的数量积可以通过坐标表示为 a·b = x1x2 + y1y2。这个公式是通过将...
在二维平面上,向量的数量积(也称为点积)定义为两个向量的模长乘积与它们之间夹角的余弦值的乘积。用公式表示为:**a·b = |a| |b| cosθ**,其中a和b是两个非零向量,θ是它们之间的夹角,|a|和|b|分别是向量a和b...
标题中的“20届高考数学一轮复习讲义(提高版) 专题5.3 平面向量的数量积及运用(原卷版)”指的是高中数学复习资料,专注于平面向量的数量积及其应用这一主题。这部分内容是针对高考复习,旨在帮助学生深入理解和...
数量积,也称为点积或内积,是两个向量之间的一种乘法运算。当我们提到两个向量a和b的数量积时,记为a·b。根据定义,它是通过一个公式来计算的:a·b=|a||b|cosθ,其中|a|和|b|分别代表向量a和向量b的模(长度)...
数量积,又称点积或内积,是两个向量的一种运算,结果是一个标量(数量)。在物理学中,数量积的概念常用于计算力对物体所做的功。 向量的数量积定义为:两个非零向量a和b的夹角为θ时,它们的数量积表示为|a| * |b...
在二维或三维空间中,向量的数量积(又称点积或标量积)是一个标量值,它表达了两个非零向量之间的几何关系,特别是它们之间的夹角信息。数量积的结果是两个向量的模长乘以它们夹角的余弦值。 **数量积的定义**: ...
《向量的数量积》 向量的数量积,也称为向量的内积,是向量代数中的一个重要概念,它将向量的运算拓展到了除加法和减法之外的另一种基本运算。数量积的引入源于物理学中的功的计算,当我们讨论一个力作用在物体上并...
首先,数量积也称为点积或内积,是两个向量的一种乘法运算,其结果是一个标量。数量积的计算公式是a·b=|a|*|b|*cosθ,其中|a|和|b|分别是向量a和b的模长,θ是两向量的夹角。根据这一公式,我们可以通过向量的点积...
数量积,也称点积或内积,是两个向量在空间中的一种特殊乘法运算。当两个非零向量垂直时,它们的数量积为零,这一点是理解数量积概念的起点。此外,数量积的结果是一个标量,而非向量,这是与向量的另一种乘法—向量...
平面向量的数量积,也称为点积或内积,是向量代数中的一个基本概念。它涉及到向量的模长、方向以及它们之间的夹角。以下是对平面向量数量积性质的详细解释: 1. **数量积为零**:如果两个非零向量a和b的数量积a·b...
该PPT深入浅出地讲解了向量的数量积(也称点积)与向量积(也称叉积)的基本概念、性质、计算方法和应用,是高等数学课程中不可或缺的一部分。 PPT内容条理清晰,逻辑严密,从向量的基本概念出发,逐步引入数量积和...
1. **向量的数量积定义**:向量a和向量b的数量积(点积)定义为a·b=|a||b|cosθ,其中|a|和|b|分别是向量a和b的模,θ是两个向量之间的夹角。数量积的结果是一个标量,表示了两个向量之间在方向上的投影乘积。 2. ...
在数学的向量代数领域中,向量的数量积(或称为点积、内积)是一个极为重要的基本概念,其定义和性质不仅对于数学专业学生来说至关重要,对于理工科学生理解物理学中力的分解和作用也具有不可或缺的作用。...
在《平面向量数量积解题策略》的复习案例中,教师引导学生通过绘制思维导图,回忆和反思知识点,逐渐形成平面向量的知识网络。在这个过程中,学生能够主动整合知识,熟练掌握解决向量数量积问题的基本方法,包括定义...