- 浏览: 124483 次
- 性别:

- 来自: 深圳
-

文章分类
最新评论
-
xuzhenAAfufang:
...
对任何一天是星期几算法的实现 -
xuzhenAAfufang:
a=(d+2*m+3*(m+1)/5+y+y/4-y/100+ ...
对任何一天是星期几算法的实现
Abstract
This paper presents new hash functions for table lookup using 32-bit or 64-bit arithmetic. These hashes are fast and reliable. A framework is also given for evaluating hash functions.
Hash tables [Knuth6] are a common data structure. They consist of an array (the hash table) and a mapping (the hash function). The hash function maps keys into hash values. Items stored in a hash table must have keys. The hash function maps the key of an item to a hash value, and that hash value is used as an index into the hash table for that item. This allows items to be inserted and located quickly.
What if an item hashes to a value that some other item has already hashed to? This is a collision. There are several strategies for dealing with collisions [Knuth6], but the strategies all make the hash tables slower than if no collisions occurred.
If the actual keys to be used are known before the hash function is chosen, it is possible to choose a hash function that causes no collisions. This is known as a perfect hash function [Fox]. This paper will deal with the other case, where the actual keys are a small subset of all possible keys.
For example, if a hash function maps 30-byte keys into a 32-bit output, it maps 2240 possible keys into 232 possible hash values. Less than 232 actual keys will be used. With a ratio of 2208 possible keys per hash value, it is impossible to guarantee that the actual keys will have no collisions.
If the actual keys being hashed were uniformly distributed, selecting the first v bits of the input to be the v-bit hash value would make a wonderful hash function. It is fast and it hashes an equal number of possible keys to each hash value. Unfortunately, the actual keys supplied by humans and computers are seldom uniformly distributed. Hash functions must be more clever than that.
This paper is organized as follows. Hash Functions for Table Lookup present the new 32-bit and 64-bit hashes. Patterns lists some patterns common in human-selected and computer-generated keys. A Hash Model names common pieces of hash functions. Funneling describes a flaw in hash functions and how to detect that flaw. Characteristics are a more subtle flaw. The last section shows that the new hashes have no funnels.
Code for the new hash function is given in figure Newhash. ^ means exclusive-or, and << and >> are left and right shift respectively (neither is a barrelshift).
typedef unsigned long int u4; /* unsigned 4-byte type */
typedef unsigned char u1; /* unsigned 1-byte type */
/* The mixing step */
#define mix(a,b,c) \
{ \
a=a-b; a=a-c; a=a^(c>>13); \
b=b-c; b=b-a; b=b^(a<<8); \
c=c-a; c=c-b; c=c^(b>>13); \
a=a-b; a=a-c; a=a^(c>>12); \
b=b-c; b=b-a; b=b^(a<<16); \
c=c-a; c=c-b; c=c^(b>>5); \
a=a-b; a=a-c; a=a^(c>>3); \
b=b-c; b=b-a; b=b^(a<<10); \
c=c-a; c=c-b; c=c^(b>>15); \
}
/* The whole new hash function */
u4 hash( k, length, initval)
register u1 *k; /* the key */
u4 length; /* the length of the key in bytes */
u4 initval; /* the previous hash, or an arbitrary value */
{
register u4 a,b,c; /* the internal state */
u4 len; /* how many key bytes still need mixing */
/* Set up the internal state */
len = length;
a = b = 0x9e3779b9; /* the golden ratio; an arbitrary value */
c = initval; /* variable initialization of internal state */
/*---------------------------------------- handle most of the key */
while (len >= 12)
{
a=a+(k[0]+((u4)k[1]<<8)+((u4)k[2]<<16) +((u4)k[3]<<24));
b=b+(k[4]+((u4)k[5]<<8)+((u4)k[6]<<16) +((u4)k[7]<<24));
c=c+(k[8]+((u4)k[9]<<8)+((u4)k[10]<<16)+((u4)k[11]<<24));
mix(a,b,c);
k = k+12; len = len-12;
}
/*------------------------------------- handle the last 11 bytes */
c = c+length;
switch(len) /* all the case statements fall through */
{
case 11: c=c+((u4)k[10]<<24);
case 10: c=c+((u4)k[9]<<16);
case 9 : c=c+((u4)k[8]<<8);
/* the first byte of c is reserved for the length */
case 8 : b=b+((u4)k[7]<<24);
case 7 : b=b+((u4)k[6]<<16);
case 6 : b=b+((u4)k[5]<<8);
case 5 : b=b+k[4];
case 4 : a=a+((u4)k[3]<<24);
case 3 : a=a+((u4)k[2]<<16);
case 2 : a=a+((u4)k[1]<<8);
case 1 : a=a+k[0];
/* case 0: nothing left to add */
}
mix(a,b,c);
/*-------------------------------------------- report the result */
return c;
}
Fitting bytes into registers
The new hash deals with blocks of 12 bytes, rather than 1 byte at a time like most hashes. The mix uses 36 instructions, which is 3 instructions per byte. Mix() allows 2::1 parallelism, so ideally it would run twice as fast on superscalar CPUs.
The new hash fits the bytes into the registers a, b, and c as efficiently as possible in a machine-independent way. Fitting bytes into registers consumes 3m instructions. (If the key were known to be an array of words, this 3m could be reduced to .75m.) The whole hash, including the mix, takes about 6m+35 instructions to hash m bytes.
The switch statement is an interesting optimization. It contains a single piece of code for handling 11-byte strings, but the suffixes of this code can handle shorter strings. The switch statement causes the program control to jump to the correct suffix, determined by the actual number of bytes remaining.
A hash for 64-bit machines
64-bit machines can hash faster and better with 64-bit arithmetic. Code for the mixing step for a hash for 64-bit machines is given in figure Hash64. The modifications needed to hash() are straightforward. It should put 24-byte blocks into 3 8-byte registers and return an 8-byte result. The 64-bit golden ratio is 0x9e3779b97f4a7c13LL.
#define mix64(a,b,c) \
{ \
a=a-b; a=a-c; a=a^(c>>43); \
b=b-c; b=b-a; b=b^(a<<9); \
c=c-a; c=c-b; c=c^(b>>8); \
a=a-b; a=a-c; a=a^(c>>38); \
b=b-c; b=b-a; b=b^(a<<23); \
c=c-a; c=c-b; c=c^(b>>5); \
a=a-b; a=a-c; a=a^(c>>35); \
b=b-c; b=b-a; b=b^(a<<49); \
c=c-a; c=c-b; c=c^(b>>11); \
a=a-b; a=a-c; a=a^(c>>12); \
b=b-c; b=b-a; b=b^(a<<18); \
c=c-a; c=c-b; c=c^(b>>22); \
}
The whole 64-bit hash takes about 5m+41 instructions to hash m bytes.
How these functions are used
These hashes work equally well on all types of input, including text, numbers, compressed data, counting sequences, and sparse bit arrays. No final mod, multiply, or divide is needed to further mix the result. If the hash value needs to be smaller than 32 (64) bits, this can be done by masking out the high bits, for example (hash&0x0000000f). The hash functions work best if the size of the hash table is a power of 2. If the hash table has more than 232 (264) entries, this can be handled by calling the hash function twice with different initial initvals then concatenating the results. If the key consists of multiple strings, the strings can be hashed sequentially, passing in the hash value from the previous string as the initval for the next. Hashing a key with different initial initvals produces independent hash values.
The rest of this paper explains the design criteria for these hash functions.
Table EMP: Is this data uniformly distributed? EMPNO ENAME JOB MGR HIREDATE SAL COMM DEPTNO
| 7369 | SMITH | CLERK | 7902 | 17-DEC-80 | 800 | 20 | |
| 7499 | ALLEN | SALESMAN | 7698 | 20-FEB-81 | 1600 | 300 | 30 |
| 7521 | WARD | SALESMAN | 7698 | 22-FEB-81 | 1250 | 500 | 30 |
| 7566 | JONES | MANAGER | 7839 | 02-APR-81 | 2975 | 20 | |
| 7654 | MARTIN | SALESMAN | 7898 | 28-SEP-81 | 1250 | 1400 | 30 |
| 7698 | BLAKE | MANAGER | 7539 | 01-MAY-81 | 2850 | 30 | |
| 7782 | CLARK | MANAGER | 7566 | 09-JUN-81 | 2450 | 10 | |
| 7788 | SCOTT | ANALYST | 7698 | 19-APR-87 | 3000 | 20 | |
| 7839 | KING | PRESIDENT | 17-NOV-81 | 5000 | 10 | ||
| 7844 | TURNER | SALESMAN | 7698 | 08-SEP-81 | 1500 | 30 | |
| 7876 | ADAMS | CLERK | 7788 | 23-MAY-87 | 1100 | 0 | 20 |
| 7900 | JAMES | CLERK | 7698 | 03-DEC-81 | 950 | 30 | |
| 7902 | FORD | ANALYST | 7566 | 03-DEC-81 | 3000 | 20 | |
| 7934 | MILLER | CLERK | 7782 | 23-JAN-82 | 1300 | 10 |
Table EMP is the standard toy database table, and a typical set of data [Oracle].
A few patterns stand out.
- ENAME and JOB are the 26 uppercase ASCII letters arranged in different orders. The numbers in EMPNO can also appear in MGR. Values consist of common substrings arranged in different orders.
- All the characters are ASCII, with the high bit of every byte set to 0. The EMPNO field is all numbers, while the ENAME field is all uppercase letters and spaces. Some rows even have identical values in some columns. Values often differ in only a few bits.
- The only difference between zero and the null value may be that the lengths are different. Also, consider the two keys "a" "aaa" "a" and "aa" "a" "aa". Lengths must be considered part of the data, otherwise such keys are indistinguishable.
- Another common pattern (not present in this example) is for keys to be nearly all zero, with only a few bits set.
Human-selected and computer-generated sets of keys almost always match at least one of these patterns. Most mappings of keys to hash values map these sets of keys quite uniformly. Unfortunately, the hash functions that are fastest and easiest to write tend to be among the rare functions that do poorly on these sets of keys.
To aid in analysis, this paper will assume that hash functions are constructed using a hash model. Although most hashes fit this model, some (for example MD4 [MD4] and Rogaway's bucket hash [Rogaway]) do not. Hash functions have some internal state, and a permutation mix is used to mix this internal state. Another function, combine, is used to combine input blocks with the current internal state.
initialize the internal state;
for (each block of the input)
{
combine (the internal state, the current input block);
mix( the internal state);
}
value = postprocess( the internal state );
return (value);
Consider the hash function XORhash:
char XORhash( char *key, int len) { char hash; int i; for (hash=0, i=0; i (XORhash requires 5m+3 instructions to hash m bytes. Compare that to 6m+35 and 5m+41 for the two new hash functions.) The internal state of XORhash is the 1-byte value hash. Each key[i] is an input block. The combining step is ^. There is no mixing step (or, the mixing step is the identity function). The postprocessing step is (hash%101).XORhash hashes the keys "ac" and "bd" to the same value. The only difference between the two keys is the first bit of each byte. What is the problem here?
Let K (keys) be the set of all k-bit values and V (hash values) be the set of all v-bit values. Let a hash function h : K -> V be given. Bit i in 1..k affects bit j in 1..v if two keys differing only at input bit i will differ at output bit j about half the time.
Define h to be a funneling hash if there is some subset t of the input bits which can only affect bits u in the internal state, and |t| > |u| and v > |u|. h has a funnel of those t input bits into those u bits of the internal state. If a hash has a funnel of t bits into u, then u of those t bits can cancel out the effects of the other |t|-|u|. The set of keys differing only in the input bits of the funnel can produce no more than half that number of hash values. (Those 2|t| keys can produce no more than 2|u| out of 2v hash values.) Differing in only a few bits is a common pattern in human and computer keys, so a funneling hash is seriously flawed.
For example, consider XORhash and 30-byte keys. All 30 lowest-order key bits funnel into only the lowest-order bit of the internal state. Every set of a billion (230) keys which differ only in the lowest order key bits maps into just 2 hash values, even though 101 hash values are available.
- The postprocessing step just selects v bits of the internal state to be the v-bit result,
- When the input block is fixed, the combining step is a reversible mapping of the internal state to the internal state,
- When the original internal state is fixed, the combining step is a one-to-one mapping (every input block value is mapped to a distinct internal state value),
- The mixing function is reversible,
- The mixing step causes every bit of the internal state to affect every bit of the result, and
- The mixing step, when run either forwards or in reverse, causes every bit of the internal state to affect at least v bits of the internal state.
- For every intermediate point in the mixing step, consider running the mixing step forward to that point from the previous combine, and backward to that point from the next combine. For every set Y of bits in the internal state in the middle, there some set X of bits in the previous input block and Z in the next input block that affect those Y bits. For every Y with less than v bits, |X|+|Z| must be less than or equal to |Y|. (Note that if every bit in the previous and next block affects at least v bits in the center of the mixing step, this requirement is satisfied.)
There is an efficient way of testing which input bits affect which output bits. For an (input bit, output bit) pair, the test is to find a key pair differing in only that input bit that changes that output bit, and another such key pair that does not change that output bit. That is really two tests, one to test that the output bit changes sometimes, and the other to test that the output bit sometimes stays the same.
How many key pairs need to be hashed? If the input bit changes the output bit with probability 1/2, the chances of the output not changing at all is 1/2 for 1 pair, 1/4 for 2 pairs, 1/8 for 3 pairs, and 2-x for x pairs. If n tests are being checked, and each test passes with probability 1/2, after log(n) pairs there is a still a (1 - 1/n)n = 1/e chance of some test not passing. However, if after 2log(n) key pairs a test has still not passed, it is safe to say that the hash fails that test. Key pairs differing in a given input bit can be used to check all output bits simultaneously. All together, it is possible to show that every input bit affects every output bit by hashing about klog(2kv) key pairs, and it is possible to show that a particular (input bit, output bit) pair fails by hashing about 2log(2kv) key pairs.
A delta is the difference (usually by XOR or subtraction) between two values. An input delta is the delta of two input keys, and an output delta is the delta of two hash values. A characteristic [Biham] is an input delta that produces a predictable output delta.
Suppose that a mixing function has a characteristic that occurs with probability 1, and it has an input delta with only t bits set and an output delta with only u bits set. If two keys differ in all t bits in block k1 and all u bits in block k2, they will produce the same internal state. That means any set of 2t+u keys differing in only those bits will produce at most 2t+u-1 distinct internal states. This is not a funnel because each of those bits alone might affect all output bits. But it has the same effect as a funnel of t+u bits into t+u-1.
Unlike funneling, there are no efficient tests known for checking for all characteristics. The test for funneling is actually a test for all k 1-bit deltas. There are (k choose x) x-bit deltas, and it quickly becomes impractical to test all of them.
Consider two keys, each of which is all zero except for one bit. They can be viewed as the same key with two substrings swapped, where the set bit was in one of the substrings. The boundaries of the substrings could be just about anything. By checking the behavior of all such pairs of keys, we can check if any two substrings are treated commutatively. This test is actually equivalent to checking for all characteristics with 2-bit input deltas.
The funneling test was used to choose the structure and constants for the mixing function of the 32 bit (64 bit) hash. By theorem Nofunnel, the new hashes have no funnels:
- The postprocessing step just selects the 32 (64) bits of c to be the result.
- The combining step (addition of the internal state and an input block) is reversible when the input block is fixed.
- The combining step is reversible (which implies one-to-one) when the internal state is fixed.
- Mix() is reversible.
- Mix() causes every bit of a, b, and c to affect every bit of the result (c) with probability 1/2+-1/6.
- Mix(), when run either forwards or in reverse, causes every bit of of a, b, and c to affect at least 32 (80) bits of a, b, and c at least 1/4 (1/2) of the time.
- This last point, actually, didn't hold for lookup2.c. There is a funnel of 32 bits to 31 bits, with those 32 bits distributed across two blocks. I backed up my computer, wrote a program that found this, then changed computers. So I don't have the code and don't remember where the funnel was. A funnel of 32 bits to 31 is awfully nonserious, though, so I let things be.
Before the final mixing step, the length is added to c. Nothing else is added to the bottom byte of c. The upper length bytes may overlap the final key block, but the upper length bytes cannot be changed without changing at least 256 bytes of the key, so this does not introduce a funnel.
Every 2-bit characteristic changes every bit as well. The least-affected output bit changes with probability 1/2+-28/100 (1/2+-1/6 for the 64-bit hash) for one 2-bit delta. The 3-bit deltas consisting of the high bits of a, b, c and the low bits of a, b, c were also tested; they changed every output bit with probability 1/2+-1/6. Tests were run both with random and with almost-all-zero keys.
The tests for funneling and simple characteristics show that the new hashes perform well when keys differ in only a few bits. They perform well on almost-all-zero keys. The tests for 2-bit characteristics also show that they do not treat any substrings commutatively. That covers all the common patterns, so these hashes should work well on all classes of keys.
Two new hash functions are given for hash table lookup. They produce full 32-bit or 64-bit results and allow hash table sizes to be a power of two. The new hashes are fast and reliable. They have no funnels, so they should work equally well on all types of keys.
Further code and analysis can be found on the web at http://burtleburtle.net/bob/hash/index.html.
Hash functions and block ciphers
Pseudorandom number generation
The birthday paradox
Examples of existing hash functions
Table of Contents
Summary
The New Hashes Have No Funnels
Characteristics
Funneling
Model for hash functions
Hash Model
Patterns
Hash64: C code for a mixing step for 64-bit machines
Newhash: C code for the new 32-bit hash
Hash Functions for Table Lookup
Introduction
发表评论
-
个人技术站点维护工具箱[转]
2007-09-30 10:44 1584转载:http://www.dbanotes.net/web ... -
分布式缓存系统Memcached简介与实践[转]
2007-09-30 10:34 6017分布式缓存系统Memcached简介与实践 缘起: 在数据 ... -
memcached 数据交换协议
2007-09-30 09:59 2550转载:http://code.sixapart.com/svn ... -
Memcached深度分析[转]
2007-09-30 09:42 5408Memcached深度分析 Memcached是dang ... -
电子商务网站重点要解决的几个问题
2007-09-15 10:15 1308转载:http://www.cnblogs.com ... -
站内搜索
2007-09-15 10:07 1284所谓的‘站内搜索’,很多人的做法是在页面上嵌入一段搜索引擎公司 ... -
什么是服务器加速技术(转载)
2007-09-07 23:53 1527获取信息的速度快慢已经成为制约互联网发展的重要因素。如何在现 ... -
CDN应用与架构
2007-09-07 23:29 1535CDN速度快、传输安全、扩展性强,尤其在应对大容量迸发时游刃有 ... -
CDN原理
2007-09-07 23:16 2339CDN(Content Delivery Network,内容 ... -
编写高性能Web应用程序的10个入门技巧(转载)
2007-09-07 22:50 1224数据层性能 技巧 1 — 返回多个结果集 技巧 2 ... -
说说大型高并发高负载网站的系统架构
2007-09-07 22:39 1407---By Michael ---转载:http://www. ...


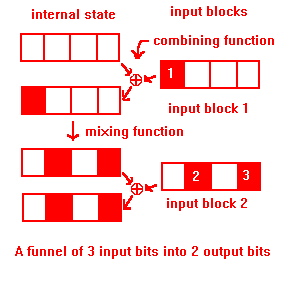 A hash function is bad if it causes collisions when keys differ in only a few bits. This always happens when a number of input bits can change only a smaller number of bits in the internal state. Funneling formalizes this concept.
A hash function is bad if it causes collisions when keys differ in only a few bits. This always happens when a number of input bits can change only a smaller number of bits in the internal state. Funneling formalizes this concept. 


相关推荐
The only source of any storage location information is the sysindexes table, which keeps track of the address of the root page for every index, and the first IAM page for the index or table....
line, then PAQ6 prompts for them, reading until the first blank line or end of file. The -3 is optional, and is used to trade off compression vs. speed and memory. Valid options are -0 to -9. Higher ...
Table of content: ----------------- - Legal issues - Donate - Register - Contributions - Latest Versions - Version Control repository - Installation - Available VCL Components - Sample applications -...
集合了 所有的 Unix命令大全 ...telnet 192.168.0.23 自己帐号 sd08077-you0 ftp工具 192.168.0.202 tools-toolss ... 各个 shell 可互相切换 ksh:$ sh:$ csh:guangzhou% bash:bash-3.00$ ... 命令和参数之间必需用空格隔...
电大职业技能实训版计算机网络技术网络管理方向专业网站美工设计基础形成性考核答案.doc
计算机等级考试一级练习题解析.doc
机械设备电气控制(含PLC)(B)答案.doc
利用综合测评板以及若干电阻、电容元件设计制作电路,以产生以下四路信号: 幅度不小于3.2V,频率在19kHz到21kHz范围内连续可调的方波脉冲信号。 与方波脉冲信号同频率的正弦波信号,要求其输出电压失真度不超过5%,峰峰值(VPP)不低于1V。 与方波脉冲信号同频率且占空比在5%到15%之间连续可调的窄脉冲信号,幅度不小于3.2V。 与正弦波信号相交的余弦波信号,相位误差不超过5°,输出电压峰峰值(VPP)不小于1V。 所有信号的输出端均需连接1kΩ负载电阻(RL),并将各路信号输出连接至测评板的指定位置。同时,需在引线处贴上对应输出信号的标签,以便于后续测试。
【目标检测】榴莲叶片病害数据集1410张YOLO-VOC格式.docx
火力发电厂机组级检修项目管理标准分析.doc
自考电子商务法概论模拟试卷.doc
数据集介绍 本数据集旨在根据品牌商家的历史订单数据,构建一个预测模型,预估用户人群在规定时间内产生购买行为的概率。
电子商务管理课程实验指导书.doc
湘潭大学移动通信实验报告实验6GSM及GPRS移动台短消息发送及接收实验.docx
网络规划与组建实训指导.doc
网络服务平台电商服务平台合作协议书.doc
【目标检测】4种铁轨表面缺陷检测数据集4020张YOLO+VOC格式.docx
罗克韦尔自动化能源管理系统概述.docx
【目标检测】空中小目标无人机检测数据集840张YOLO+VOC.docx
计算机信息系统集成资质等级评定条件(修定版).doc